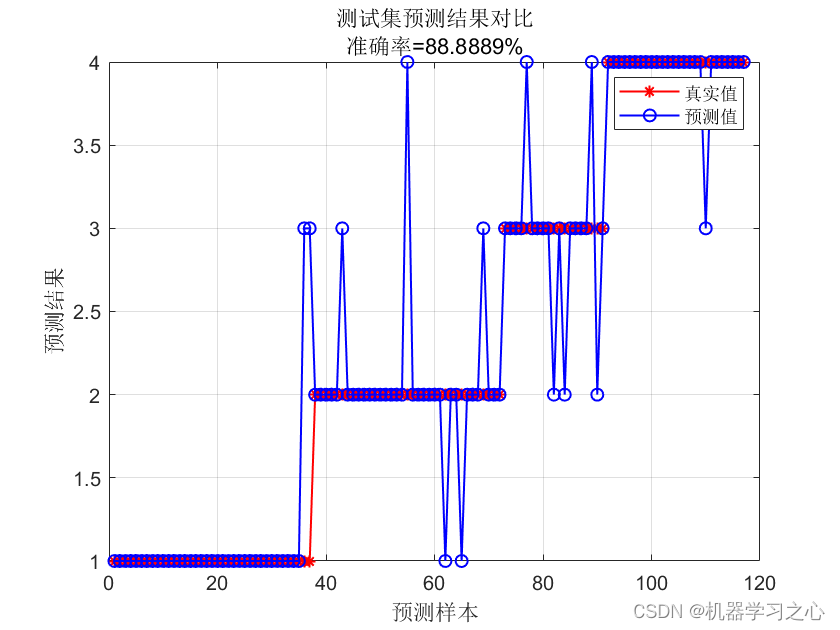
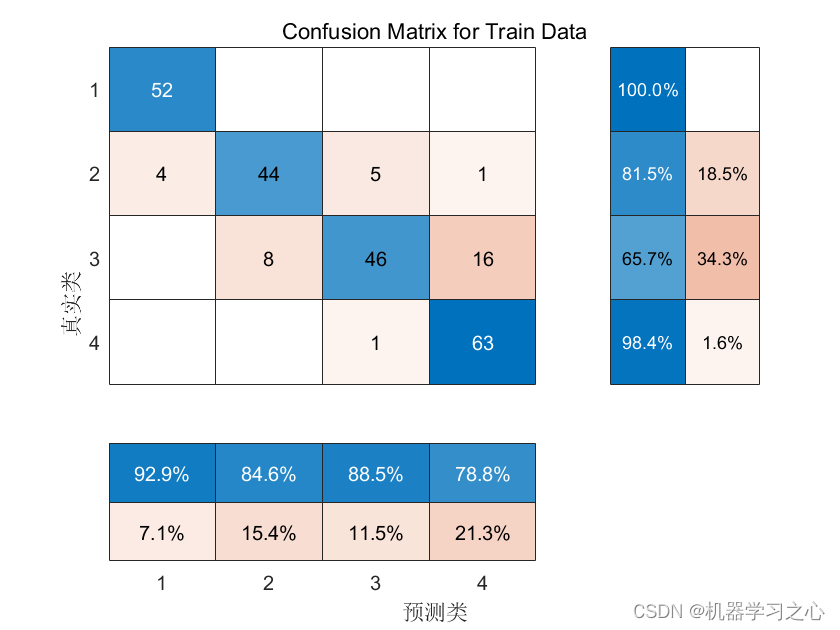
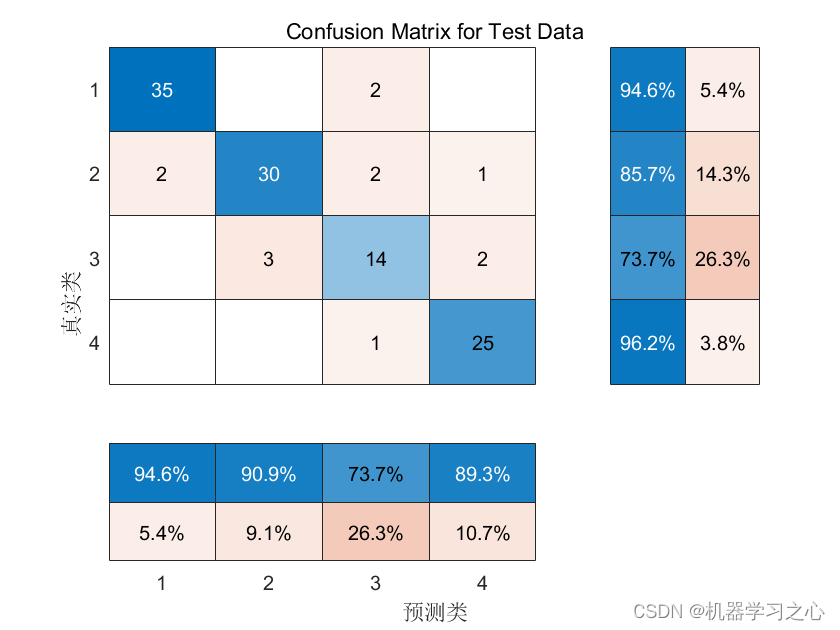
故障诊断 | 一文解决，PLS偏最小二乘法的故障诊断（Matlab）
相关文章：
故障诊断 | 一文解决，PLS偏最小二乘法的故障诊断（Matlab）
效果一览 文章概述 故障诊断 | 一文解决，PLS偏最小二乘法的故障诊断（Matlab） 模型描述 偏最小二乘法（Partial Least Squares, PLS）是一种统计建模方法，用于建立变量之间的线性关系模型。它是对多元线性回归方法的扩展，特别适用于处理高维数据和具有多重共线性的数据集。…...
我为什么选择成为程序员？
前言： 我选择成为程序员不是兴趣所在，也不是为了职业发展，全是生活所迫！ 第一章：那年，我双手插兜，对外面的世界一无所知 时间回到2009年，时间过得真快啊，一下就是15年前…...
Open CASCADE学习|统计形状拓扑数量
边界表示法（Boundary Representation，简称B-Rep）是几何造型中最成熟、无二义的表示法。它主要用于描述物体的几何信息和拓扑信息。在边界表示法中，一个实体（Solid）由一组封闭的面（Faceÿ…...
LeetCode 热题 100 题解（二）：双指针部分（2）| 滑动窗口部分（1）
题目四：接雨水（No. 43） 题目链接：https://leetcode.cn/problems/trapping-rain-water/description/?envTypestudy-plan-v2&envIdtop-100-liked 难度：困难 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图&am…...
常用的深度学习自动标注软件
0. 简介 自动标注软件是一个非常节省人力资源的操作，而随着深度学习的发展，这些自动化标定软件也越来越多。本文章将会着重介绍其中比较经典的自动标注软件 1. AutoLabelImg AutoLabelImg 除了labelimg的初始功能外，额外包含十多种辅助标注…...
选择程序员是为什么？
本章节是关于为什么会选择一名程序员的经验分享 首先，我为什么会选择这个方向，可能是因为钱多，学东西不就是为了赚钱嘛？这是一点，不过最让我接收这个行业的是好奇世界的新大陆，可以简单的说就是，…...
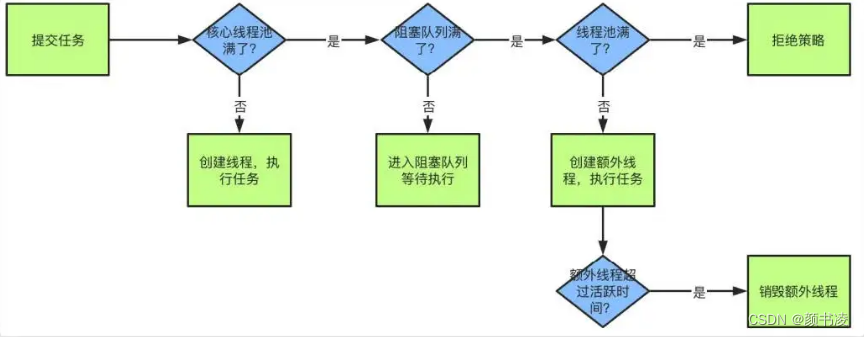
线程池参数如何设置
线程池参数设置 hello丫，各位小伙伴们，好久不见了！ 下面，我们先来复习一下线程池的参数 1、线程池参数有哪些？ corePoolSize（核心线程数）：线程池中的常驻核心线程数。即使这些线程…...
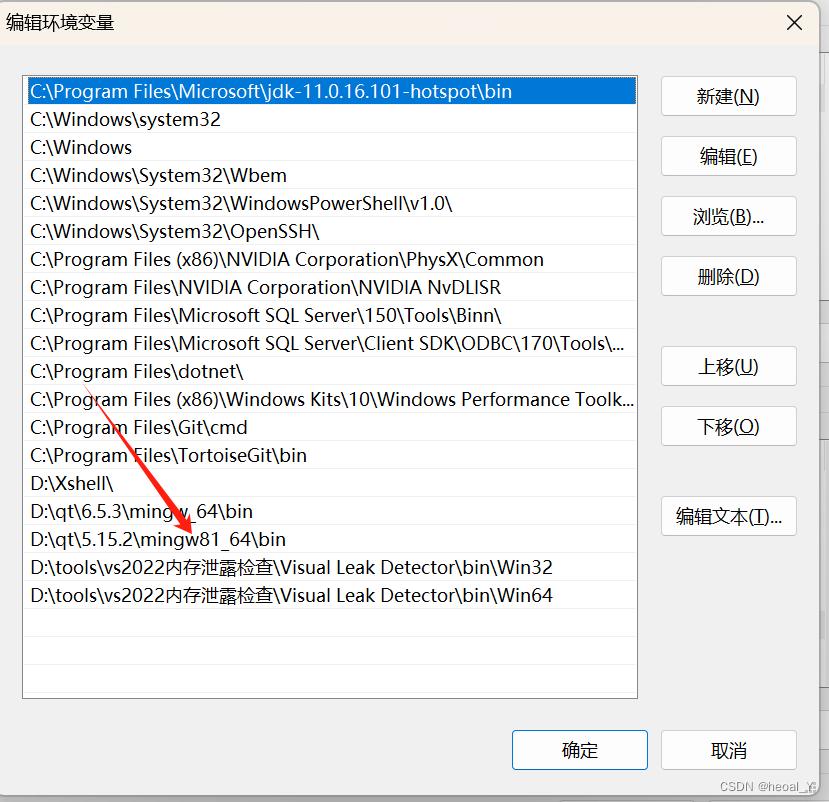
qt环境搭建-镜像源安装Qt Creator（5.15.2）以及配置环境变量
前言： 版本：5.15.2 镜像源：ustc与清华 纯小白，找了半天的镜像源安装qtcreator，搞了半天结果安装的是最新的，太新的对小白很不友好，bug比较多，支持的系统也不全，口碑不…...
SQL Server详细安装使用教程
1.安装环境 现阶段基本不用SQL Server数据库了，看到有这样的分析话题，就把多年前的存货发一下，大家也可以讨论看看，思路上希望还有价值。 SQL Server 2008 R2有32位版本和64位版本，32位版本可以安装在Windows XP及以上…...
深度解读C++17中的std::string_view：解锁字符串处理的新境界
深入研究C17中的std::string_view：解锁字符串处理的新境界 一、简介二、std::string_view的基础知识2.1、构造函数2.2、成员函数 三、std::string_view为什么性能高？四、std::string_view的使用陷阱五、std::string_view源码解析六、总结 一、简介 C中有…...
汇编基础-----常见命令基本使用
汇编基础-----常见命令基本使用 MOV：将数据从一个位置复制到另一个位置。 MOV destination, source例如： MOV RAX, RBX ; 将RBX寄存器中的值复制到RAX寄存器中ADD/SUB：将两个操作数相加或相减。 ADD destination, source SUB destinatio…...
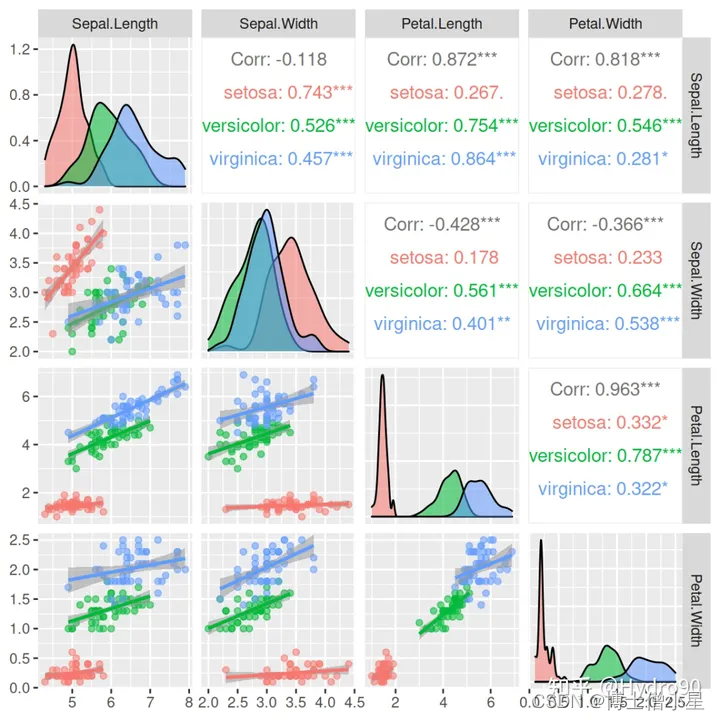
科研学习|可视化——相关性结果的可视化
一、相关性分析介绍 相关性分析是指研究两种或者两种以上的变量之间相关关系的统计分析方法，一般分析步骤为： 1）判断变量间是否存在关联；2）分析关联关系（线性/非线性）、关联方向（正相…...
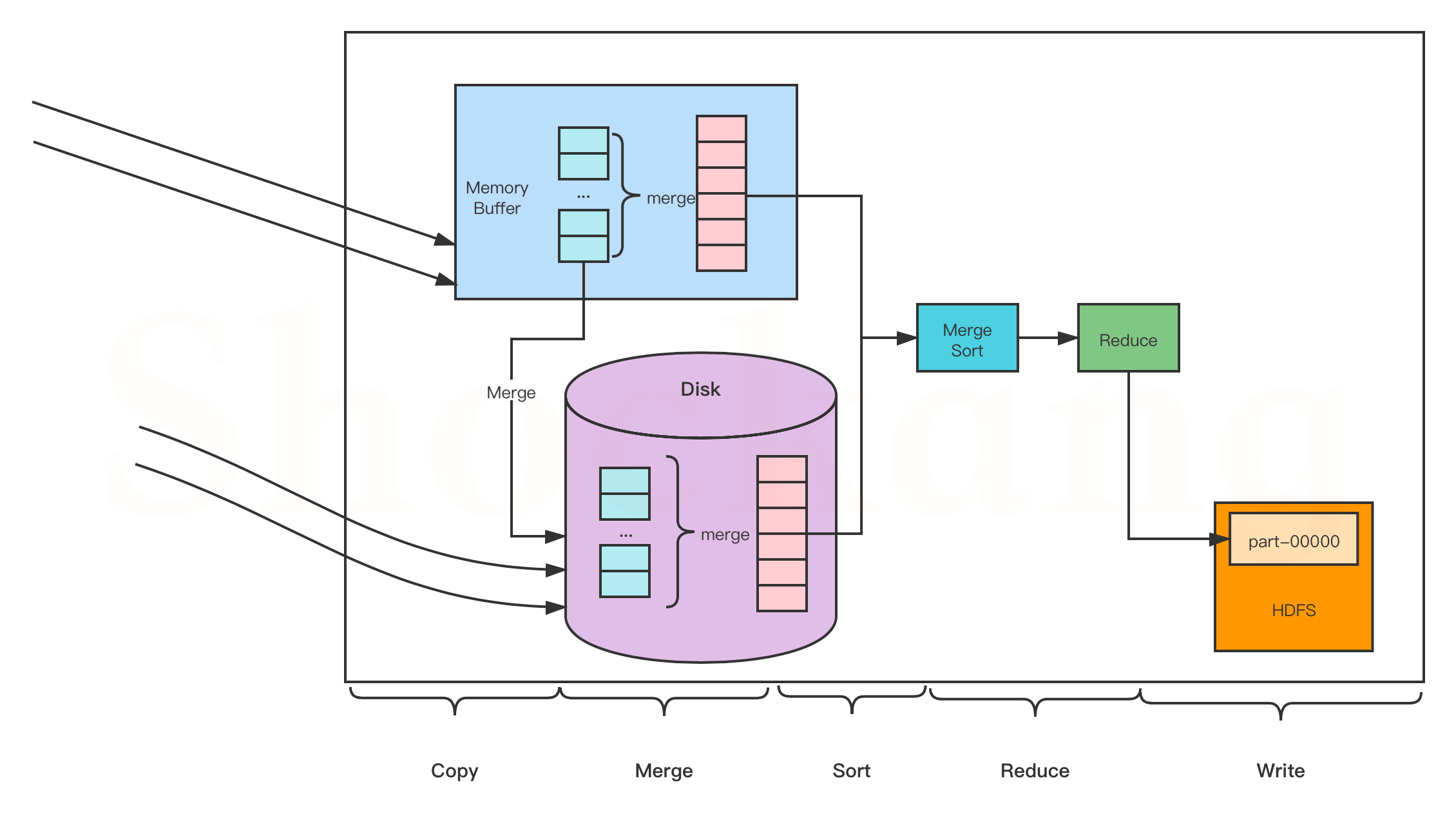
MapReduce过程解析
一、Map过程解析 Read阶段：MapTask通过用户编写的RecordReader，从输入的InputSplit中解析出一个个key/value。Map阶段：将解析出的key/value交给用户编写的Map()函数处理，并产生一系列的key/value。Collect阶段：在用户编…...
速看！这8道嵌入式面试题你都会吗？
大家好，我是知微！ 正逢求职季，分享一些嵌入式面试当中经常会遇到的题目，希望这些干货对小伙伴们面试有用哦！ 1、介绍一下static关键字的作用 在C语言中，static 关键字有几种不同的作用，根据其…...
基于SSM的电影网站（有报告）。Javaee项目。ssm项目。
演示视频： 基于SSM的电影网站（有报告）。Javaee项目。ssm项目。 项目介绍： 采用M（model）V（view）C（controller）三层体系结构，通过Spring SpringMv…...
SOCKS代理是如何提高网络性能和兼容性的？
SOCKS代理作为一种网络协议中间件，不仅在提升网络隐私和安全性方面发挥着重要作用，也在提高网络性能和兼容性方面有着不容忽视的影响🚀。本文将深入探讨SOCKS代理如何通过减少网络延迟🚀、优化数据传输🔄、提高跨平台兼…...
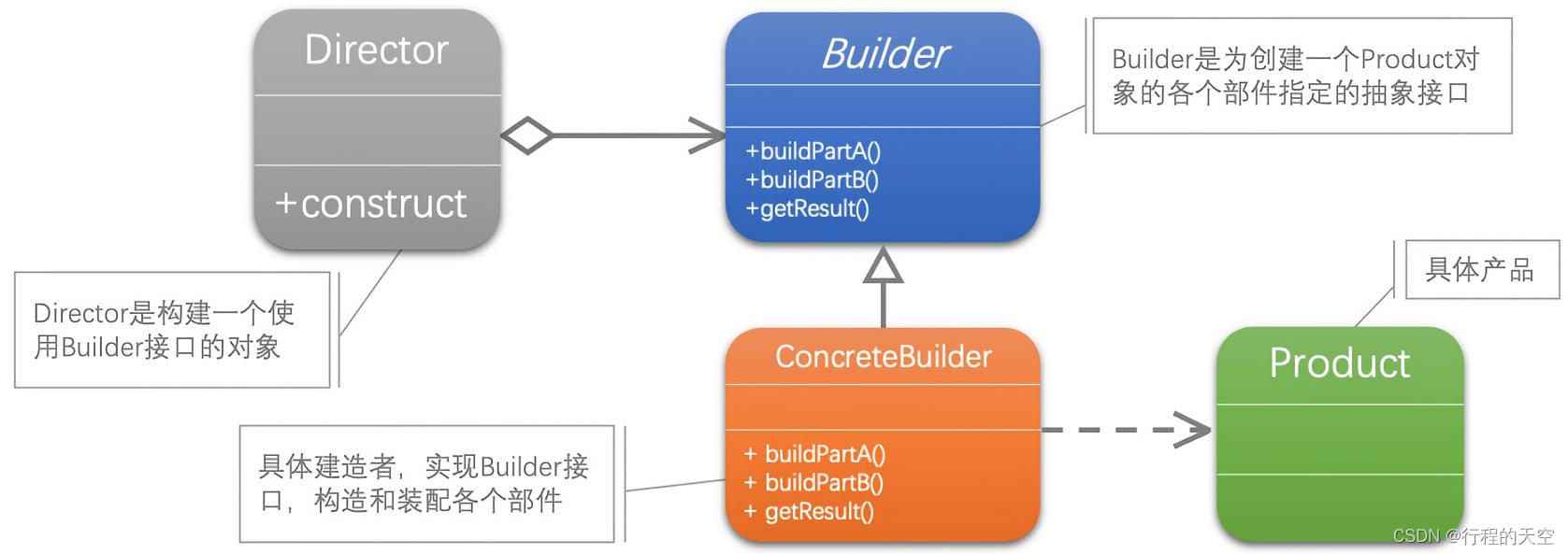
好菜每回味道不同--建造者模式
1.1 炒菜没放盐 中餐，老板需要每次炒菜，每次炒出来的味道都有可能不同。麦当劳、肯德基这些不过百年的洋快餐却能在有千年饮食文化的中国发展的那么好呢？是因为你不管何时何地在哪里吃味道都一样，而鱼香肉丝在我们中餐却可以吃出上…...
RuoYi-Cloud下载与运行
一、源码下载 若依官网：RuoYi 若依官方网站 鼠标放到"源码地址"上，点击"RuoYi-Cloud 微服务版"。 跳转至Gitee页面，点击"克隆/下载"，复制HTTPS链接即可。 源码地址为：https://gitee.com/y_project/RuoYi-Cloud.git 点击复制 打开IDEA，选…...
Vue2.x计算属性
1.计算属性 在Vue 插值表达式内实现一些操作其实非常便利，但如果表达式的逻辑过于复杂，会让插值过于臃肿且难以维护。这时可以考虑使用Vue的计算属性 1.1 不使用计算属性的例子 <!DOCTYPE html> <html><head><meta charset"…...
自动引入组件和自动生成路由的方法介绍)
Vue中使用require.context()自动引入组件和自动生成路由的方法介绍
目录 一、自动引入组件 1、语法 2、使用 2.1、在compoents文件下随便创建index.js文件 2.2、mian.js引入该js 二、自动生成路由 1、示例： 2、使用 2.1、在router文件下随便创建autoRouter.js文件 2.2、在router文件下index.js文件中引入autoRouter.js文件…...
网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞！！！ 抽象 现代智能交通系统 （ITS） 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 （…...
【kafka】Golang实现分布式Masscan任务调度系统
要求： 输出两个程序，一个命令行程序（命令行参数用flag）和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽，然后将消息推送到kafka里面。 服务端程序： 从kafka消费者接收…...
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1） にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために ＆ ように（３）そう（４）にする3、…...
条件运算符
C中的三目运算符（也称条件运算符，英文：ternary operator）是一种简洁的条件选择语句，语法如下： 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true，则整个表达式的结果为“表达式1”…...
Map相关知识
数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...
Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学？传统医学奠基期（远古 - 17 世纪）近代医学转型期（17 世纪 - 19 世纪末）现代医学成熟期（20世纪至今） 中医的源远流长和一脉相承远古至…...
Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程，代码下载：这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中，**知识蒸馏（Knowledge Distillation）**被广泛应用，作为提升模型…...
Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时，显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
探索Selenium：自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...