贪心算法|435.无重叠区间
力扣题目链接
class Solution {
public:// 按照区间右边界排序static bool cmp (const vector<int>& a, const vector<int>& b) {return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0) return 0;sort(intervals.begin(), intervals.end(), cmp);int count = 1; // 记录非交叉区间的个数int end = intervals[0][1]; // 记录区间分割点for (int i = 1; i < intervals.size(); i++) {if (end <= intervals[i][0]) {end = intervals[i][1];count++;}}return intervals.size() - count;}
};写算法题是需要集中注意力,静下心用心去写的。
如果你浮躁的话会发现理解不了,你如果静下心一步一步去画理清自己思路其实还是很容易的。
代码随想录 (programmercarl.com)
思路
相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?
其实都可以。主要就是为了让区间尽可能的重叠。
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
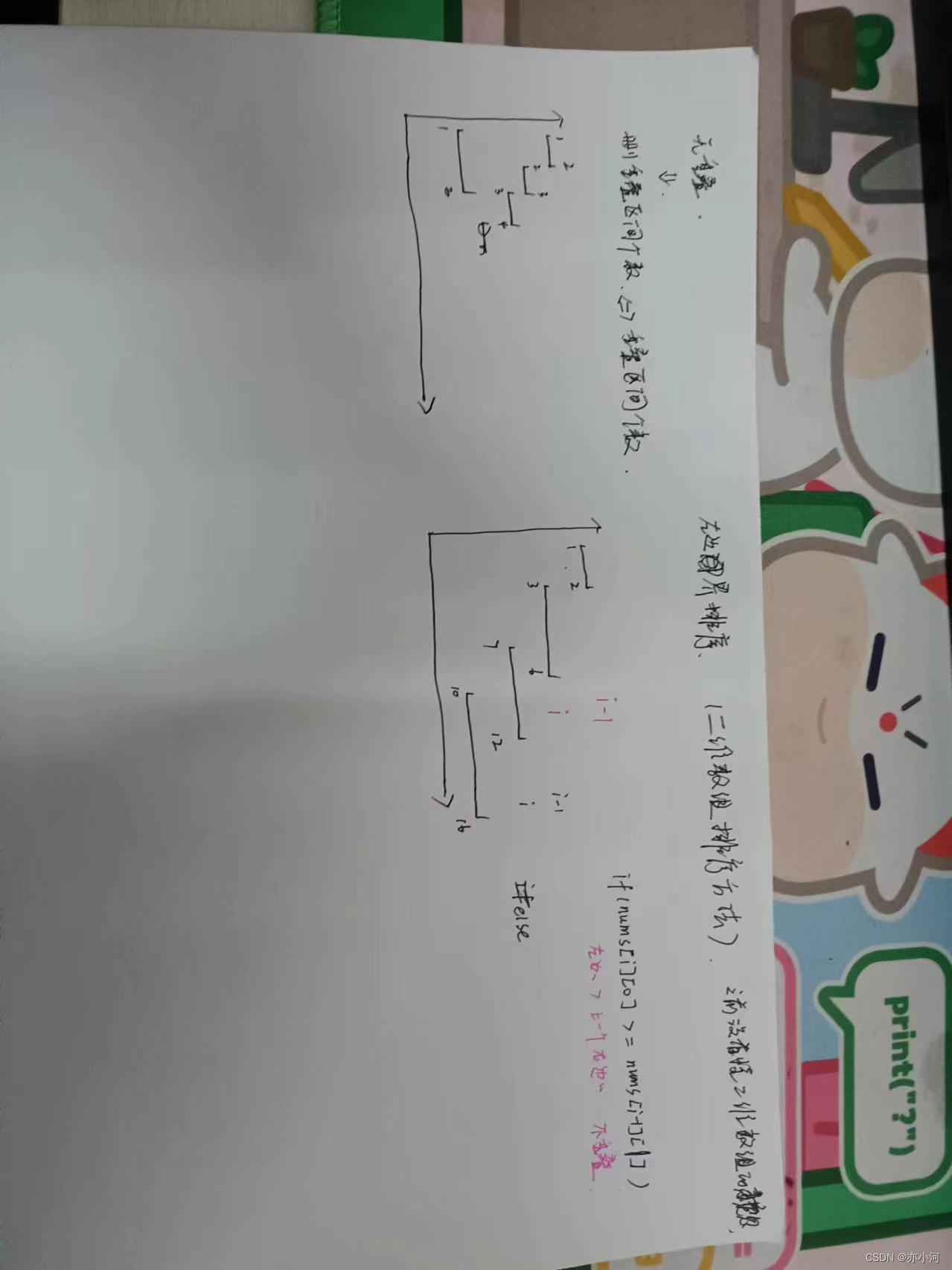
这里记录非交叉区间的个数还是有技巧的,如图:

区间,1,2,3,4,5,6都按照右边界排好序。
当确定区间 1 和 区间2 重叠后,如何确定是否与 区间3 也重贴呢?
就是取 区间1 和 区间2 右边界的最小值,因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分,如果这个最小值也触达到区间3,那么说明 区间 1,2,3都是重合的。
接下来就是找大于区间1结束位置的区间,是从区间4开始。那有同学问了为什么不从区间5开始?别忘了已经是按照右边界排序的了。
区间4结束之后,再找到区间6,所以一共记录非交叉区间的个数是三个。
总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。
自己的理解:
刚开始一直静不下心去写,然后有些地方看不懂。
后来自己去看视频静下心去理解,梳理自己的思路。
卡哥视频讲的是按左区间排序,但是这个代码答案是右区间排序哦!
而且计算的count还是不重叠部分的。
1.注意i是从1开始,这样才能和前面的有所比较
2.判断区间是否重叠
上一个区间的右区间 <= 当前区间的左区间 (不重叠)
else 重叠
因为计算的是不重叠的count
所以不重叠count++
更改end
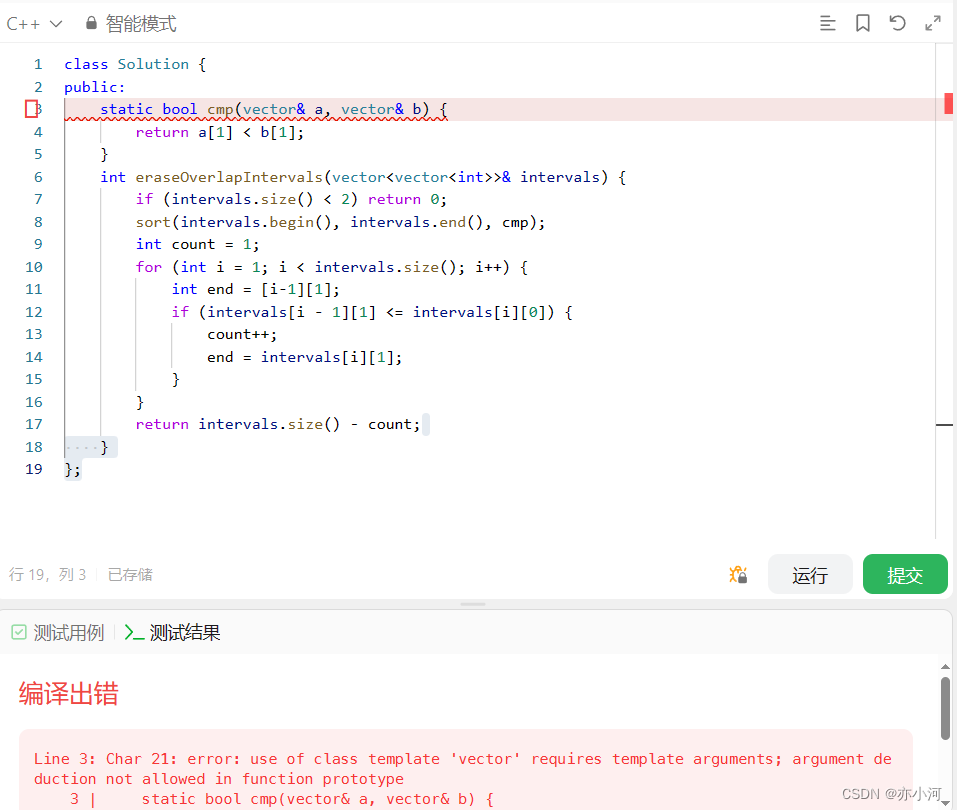
理解后独自敲的代码,语法不熟练啊!
还有可笑的错误!
相关文章:

贪心算法|435.无重叠区间
力扣题目链接 class Solution { public:// 按照区间右边界排序static bool cmp (const vector<int>& a, const vector<int>& b) {return a[1] < b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.siz…...
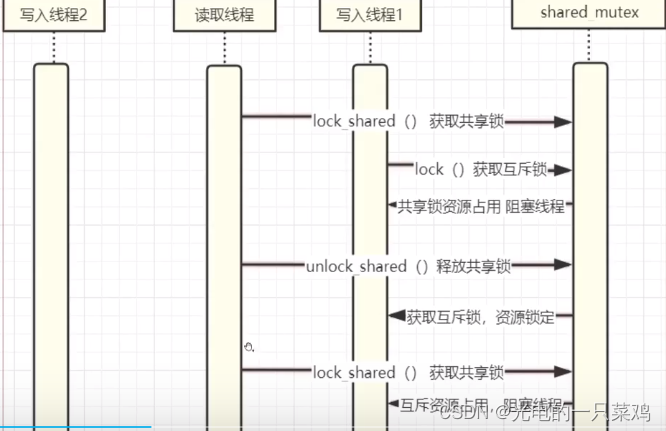
C++的并发世界(七)——互斥锁
0.死锁的由来 假设有两个线程T1和T2,它们需要对两个互斥量mtx1和mtx2进行访问。而且需要按照以下顺序获取互斥量的所有权: -T1先获取mte1的所有权,再获取mt2的所有权。 -T2先获取 mtx2的所有权。再铁取 mtx1的所有权。 如果两个线程同时执行,…...
NI-LabView的DAQ缺少或丢失的解决办法(亲测有效)
DAQmx在Labview中不显示或缺失 问题:在NI Packasge Manager安装完DAQ后在labview中不显示控件解决办法 问题:在NI Packasge Manager安装完DAQ后在labview中不显示控件 在打开测量I/O时,见不到 DAQmx,或者在Express中见不到DAQ助手…...

cesium 调整3dtiles的位置 世界坐标下 相对坐标下 平移矩阵
cesium调整3dtiles的位置用到的是平移矩阵,原理是在世界坐标系中用偏移点减去原始点得到一个平移向量,再根据这个向量得到平移矩阵。 原始点:一般是模型的中心点位置,可通过模型的包围盒得到偏移点:可分为两种情况&…...

flutter跑通腾讯云直播Demo
运行示例 前提条件 要求java jdk 11版本 并且配置到了环境变量 重要 要求flutter 版本 2.8.0 并且配置到了环境变量 重要 要求dart-sdk版本2.15 并且配置到了环境变量 重要 您已 注册腾讯云 账号,并完成 实名认证。 申请 SDKAPPID 和 SECRETKEY 登录实时音视频控…...

飞机降落蓝桥杯[2023蓝桥省赛B组]
2023蓝桥省赛B组 B题 飞机降落 题解 标准深搜板子题,难度不大 #include<bits/stdc.h> using namespace std; #define MAX 10 struct node{int t,d,l;//t:飞机到达时间 d:飞机最大盘旋时间 l:飞机降落所需时间bool v;//标记此架飞机是否被搜索过 用于剪枝 };…...

如何动态渲染HTML内容?用v-html!
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

EFcore 6 连接oracle19 WinForm vs2022
用EFcore访问Oracle,终于不需要Oracle的什么安装包了,直接在VS2022中就可以轻松搞定。在csdn上看到一哥们的帖子,测试了一下,发现很方便。使用的场景是:VS2022中EFcore6。经过测试,同 Navicat Premium 16比…...
 Object Pascal 学习笔记---第9章第2节(finally代码块))
(delphi11最新学习资料) Object Pascal 学习笔记---第9章第2节(finally代码块)
9.2 finally 代码块 还有第四个用于异常处理的关键字,我已经提到过,但到目前为止还没有使用过,那就是 finally。finally块用于执行一些应始终执行的操作(通常是清理操作)。事实上,无论是否发生异常&…...
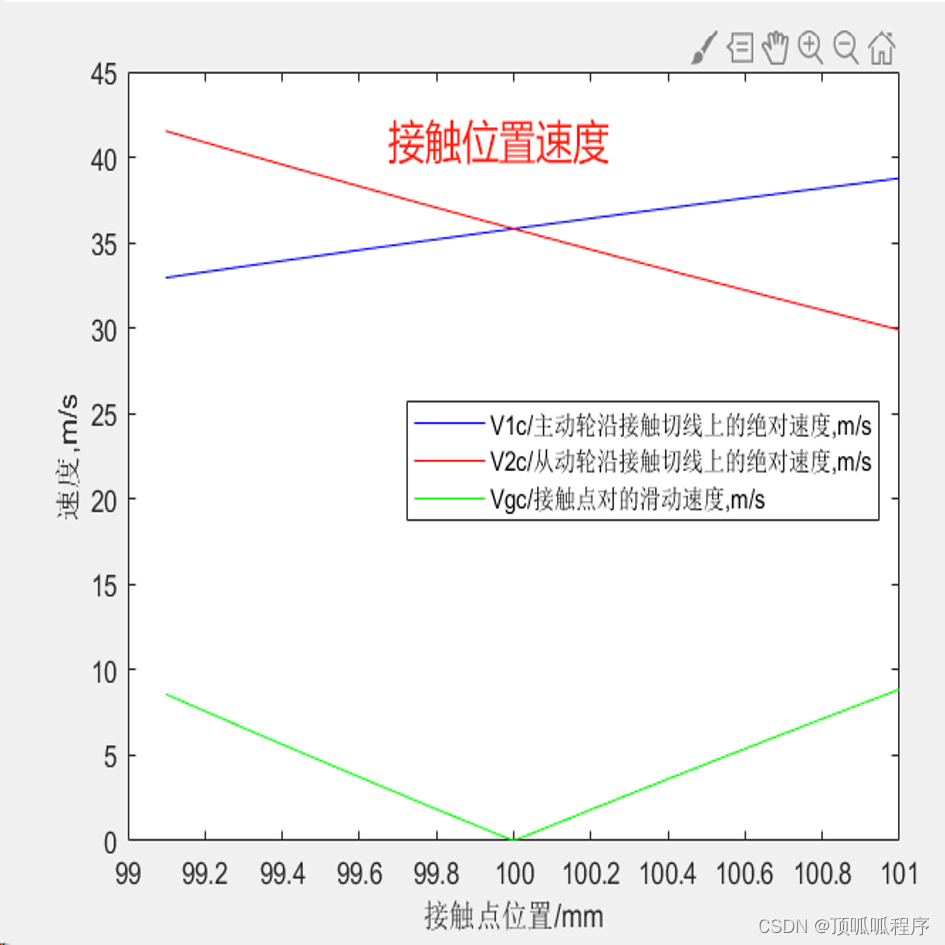
220 基于matlab的考虑直齿轮热弹耦合的动力学分析
基于matlab的考虑直齿轮热弹耦合的动力学分析,输入主动轮、从动轮各类参数,考虑润滑油温度、润滑油粘度系数等参数,输出接触压力、接触点速度、摩擦系数、对流传热系数等结果。程序已调通,可直接运行。 220直齿轮热弹耦合 接触压力…...
Intrigue Core:一款功能强大的攻击面枚举引擎
关于Intrigue Core Intrigue Core是一款功能强大的开源攻击面枚举引擎,该工具可以帮助广大研究人员更好地管理应用程序的攻击面。 Intrigue Core集成了各种各样的安全数据源,可以将这些数据提取到标准化的对象模型中,并通过图形数据库跟踪关…...

【精品PPT】智慧路灯大数据平台整体建设实施方案(免费下载)
1、知识星球下载: 如需下载完整PPTX可编辑源文件,请前往星球获取:https://t.zsxq.com/19QeHVt8y 2、免费领取步骤: 【1】关注公众号 方案驿站 【2】私信发送 【智慧路灯大数据平台】 【3】获取本方案PDF下载链接,直…...
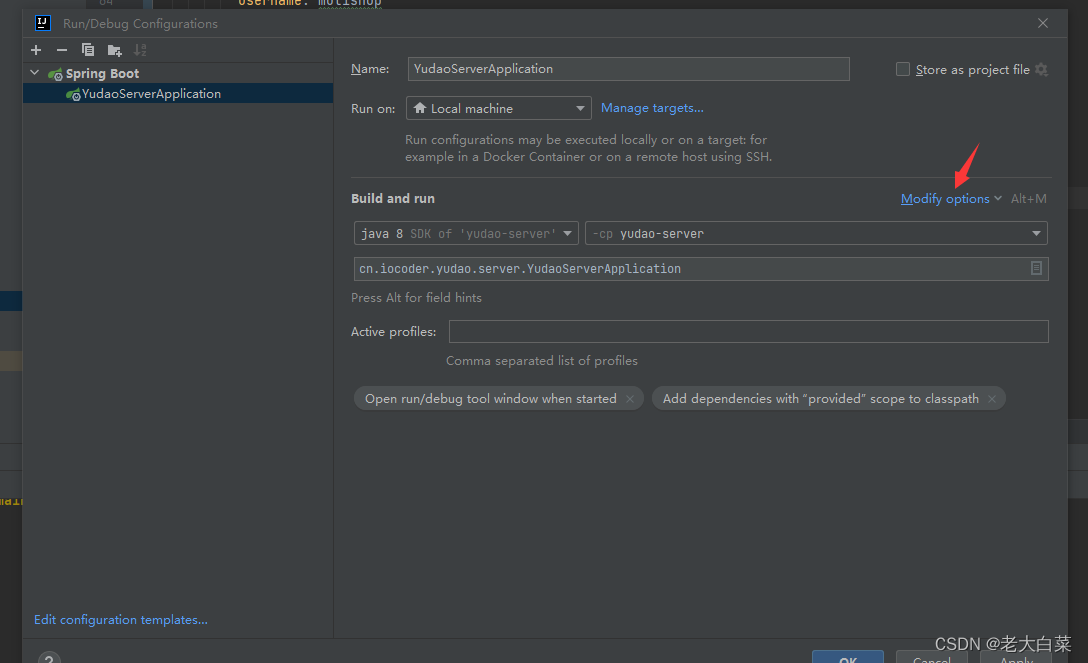
idea 中运行spring boot 项目报 Command line is too long的解决办法。
Command line is too long 在这里选择edit configures 选择shrten command line , 选择 jar manifest 运行即可。...

Windows终端添加git bash
环境:windows11 终端:windows terminal git bash默认的界面不太好看,添加到终端会比较好用 步骤 打开 windows terminal,在向下箭头 点击 设置左侧栏 点击 “添加新配置文件”,如下图配置,主要修改项&…...
【方法】PDF密码如何取消?
对于重要的PDF文件,很多人会设置密码保护,那后续不需要保护了,如何取消密码呢? 今天我们来看看,PDF的两种密码,即“限制密码”和“打开密码”,是如何取消的,以及忘记密码的情况要怎…...
怎么开发一个预约小程序_一键预约新体验
预约小程序,让生活更便捷——轻松掌握未来,一键预约新体验 在快节奏的现代生活中,我们总是在不断地奔波,为了工作、为了生活,不停地忙碌着。然而,在这繁忙的生活中,我们是否曾想过如何更加高效…...
JavaScript_注释数据类型
JavaScript_语法_注释&数据类型: 1.2注释: 1.单行注释://注释内容 2.多行注释:/*注释内容*/ 1.3数据类型: 1.原始数据类型(基本数据类型):(只有这五种) 1.number:数字…...

蓝桥杯2020年第十一届省赛 CC++ 研究生组2.0
约数个数 #include<iostream> #include<cmath> using namespace std; int main(){int n 78120, ans 0, sqr sqrt(n);for(int i 1; i < sqr; i){if(n % i 0){ans;//printf("%d,", i);if(i * i ! n) {ans;//printf("%d,", n / i);}}}//…...

SOCKS5代理、代理IP、跨界电商、游戏技术与网络安全的综合探讨
在全球经济一体化的大背景下,"出海"已成为许多企业尤其是电商和游戏行业的重要战略方向。然而,随着企业业务的扩展到海外市场,网络安全、数据隐私和内容访问等问题也随之而来。本文将深入探讨SOCKS5代理、代理IP在跨界电商和游戏行…...

关于HTTP1.0、1.1、1.x、2.0、3.0与HTTPS之间的理解
关于HTTP1.0、1.1、1.x、2.0、3.0与HTTPS之间的理解 HTTP的由来 HTTP是Hyper Text Transfer Protocol(超文本传输协议)的缩写。它的发展是万维网协会(World Wide Web Consortium)和Internet工作小组IETF(Internet Eng…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
