【LeetCode】单调栈类题目详解
所有题目均来自于LeetCode,刷题代码使用的Python3版本

单调栈
通常针对一维数组的问题,如果需要寻找一个元素右边或者左边第一个比自己大或者小的元素的位置,就可以使用单调栈,时间复杂度为O(n)
单调栈的本质是空间换时间, 遍历的过程中需要使用一个栈记录右边第一个比当前元素高的值。优点是整个数组只需要遍历一次。
使用单调栈需要明确的几点:
- 单调栈中存放的元素是什么?
- 单调栈里的元素是递增还是递减?
单调栈中的元素可以是递增的也可以是递减的,具体需要看题目的需求。
单调栈中存放的元素最好是下标,这样具有更好的泛型
练习题
739、每日温度
使用单调栈的方式从前往后进行遍历;
栈中的元素从栈底到栈顶对应下标的值是递减的,直到找到一个比栈顶元素大的值,然后出栈。
栈中存放的是元素的下标,如果出现一个新的元素比栈中元素都要大的时候,就对栈中元素进行循环遍历,将其对应的res值修改为当前元素的下标和栈中存放的值的差值,这就是最终结果,到最后一个元素的时候,因为初始化结果列表中元素值都是0,故不需要进行修改。
初始化答案res为全0的列表,这样可以防止后面的元素没有下一个更大的元素,当然这一点要根据题目的要求来,因为有些题目会赋值为-1。
class Solution:def dailyTemperatures(self, temperatures: List[int]) -> List[int]:res = [0] * len(temperatures)st = []# 从前往后进行遍历for index, temp in enumerate(temperatures):# st不为空且温度大于栈顶元素while st and temperatures[st[-1]] < temp:j = st.pop()# 题目中问的是下一个更高温度出现在几天之后 因此用下标之差表示即可res[j] = index - jst.append(index)return res

496、下一个更大元素I

直接寻找
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:res = [-1]*len(nums1)# 寻找下一个更大的元素for index,n1 in enumerate(nums1):startindex = nums2.index(n1)for n in nums2[startindex+1:]:if n>n1:res[index] = nbreakreturn res
使用单调栈
题目中有**【需要寻找最近一个比其大的元素】** 这样的字眼,就可以使用 【单调栈】
本题需要注意的是题目中存在两个数组,寻找第一个数组在第二个数组元素中下一个比对应元素大的元素。题目中说了两个数组中是没有重复元素的,可以采用单调栈+哈希表的方式进行解决。
单调栈解决的是nums2中每个元素对应的下一个比其大的元素
哈希表解决的是用来存储每个元素对应的下一个元素值,这样方便对nums1进行遍历时的查找
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:st = []res = [-1]*len(nums2)for index,num in enumerate(nums2):# print(index,num)while st and nums2[st[-1]]<num:j = st.pop()res[j] = numst.append(index)# 使用zip通过两个可迭代的对象构造字典myhash = dict(zip(nums2,res))ans = []for n1 in nums1:ans.append(myhash[n1])return ans
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:myhash = {}st = []res = []for index, n in enumerate(nums2):while st and nums2[st[-1]] < n:myhash[nums2[st.pop()]] = nst.append(index)for n1 in nums1:res.append(myhash.get(n1, -1))return res
503、下一个更大元素II

出现这种需要循环才能判断的情况,可以采用求余数的方法来多遍历一次。
类似的思路还有打家劫舍II中头尾不能同时偷的情况,就可以采用将数组(列表)进行拆分:0-n-1和1-n的情况
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:# 如何解决循环的问题?# 循环也就最多循环一轮到自己本身# 用求余来表示res = [-1] * len(nums)st = []for index, n in enumerate(nums * 2):while st and nums[st[-1]] < n:res[st.pop()] = nst.append(index % len(nums))return res
42、接雨水

在做本题之前,需要明确计算的方法是按照行进行计算还是按照列进行计算,这两个计算方法的不同会导致不同的做法。
按照行去计算的做法如下所示:逐行进行累加
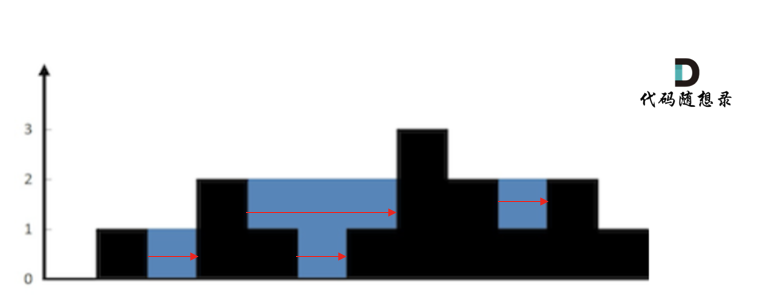
按照列去计算的做法如下所示:逐列进行累加
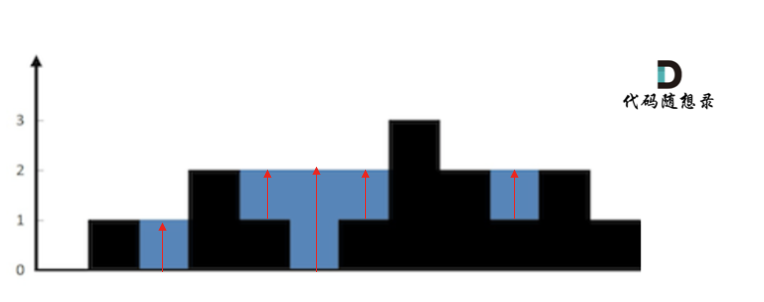
按照列去计算的时候可以假设每一列的宽度为1,只需要逐列去进行累加即可得到最终结果,这个思路也衍生了下面的暴力算法:
暴力算法的思路是一列一列的去记录能够装的雨水是多少,最终累加起来。
记录每个节点左边和右边的最大高度,然后用两个最大高度中的最小值减去当前高度,然后乘以宽度1,将这个值累加到res中。
s = (min(lHeight,rHeight)-height[i]) * 1
当遍历到第一个柱子和最后一个柱子的时候,不需要计算面积。对于其余的柱子,需要寻找其左边和右边的最高的柱子,然后取两者中的最小值,用最小值的高度减去height[i],得到差值就是可以装的雨水的高度,然后用这个高度再乘以宽度1,就是能装的雨水的体积。最后一直累加这个和,得到能装的最多的雨水。
lHeight = height[i]
rHeight = height[i]
for j in range(i + 1, len(height)):rHeight = max(rHeight, height[j])
for j in range(i - 1, -1, -1):lHeight = max(lHeight, height[j])
res += min(lHeight, rHeight) - height[i]
很不幸代码超时了。
class Solution:def trap(self, height: List[int]) -> int:# 暴力算法(从前往后进行遍历)记录当前位置左右的最高点res = 0for i in range(1, len(height) - 1):lHeight = height[i]rHeight = height[i]for j in range(i + 1, len(height)):rHeight = max(rHeight, height[j])for j in range(i - 1, -1, -1):lHeight = max(lHeight, height[j])res += min(lHeight, rHeight) - height[i]# print(i,lHeight,rHeight res += min(lHeight, rHeight) - height[i]return res
在暴力算法中,每轮循环都需要重复去寻找当前位置左右更高的高度,可以采用双指针的方法进行优化:
注意:双指针方法和暴力算法本质上都是逐列进行累加的。
通过两个单独的for循环,得到lHeight和rHeight数组(分别表示每个柱子左右两侧的最高的高度是多少),然后在通过一次循环,从1遍历到n-2位置的柱子,然后累加最终能够装的雨水的体积。
这里需要注意在循环的时候,需要进行赋初始值,例如找左侧最大值的时候,下标为0的地方赋初值height[0]不需要进行比较,然后从下标1到n-1进行遍历。具体的可以参考下图
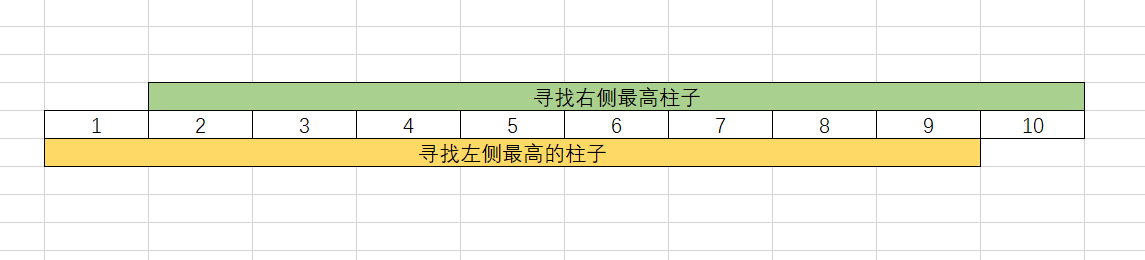
rHeight = [0] * n
lHeight = [0] * n
# 计算每个柱子左侧的最高高度
lHeight[0] = height[0]
for i in range(1, n - 1):lHeight[i] = max(lHeight[i - 1], height[i])
# print(lHeight)
rHeight[n - 1] = height[n - 1]
for i in range(n - 2, -1, -1):rHeight[i] = max(rHeight[i + 1], height[i])
找到左边和右边的最高值,计算一列可以装的水有多少
记录每个柱子左边的最高高度和右边的最高高度,然后高度就是min(左边最高高度,右边最高高度)-height[i],宽度就是1
class Solution:def trap(self, height: List[int]) -> int:# 双指针n = len(height)if n<=2:return 0res = 0lheight = [0]*nrheight = [0]*nlheight[0] = height[0] # 进行初始化for i in range(1,n-1):lheight[i] = max(lheight[i-1],height[i])rheight[n-1] = height[n-1] # 进行初始化for i in range(n-2,-1,-1):rheight[i] = max(rheight[i+1],height[i])# print(lheight,rheight)for i in range(1,n-1):res += min(lheight[i],rheight[i])-height[i]return res
单调栈的核心思路是逐行进行累加
单调栈的思路就是如果栈为空,则先第一个柱子入栈,紧接着如果第二个柱子的高度低于栈中柱子的高度,则继续入栈。也就是说此时栈中的元素从栈顶到栈底是从小到大的顺序。只有从小到大的顺序才能够再下一次遇到一个比栈顶元素高的柱子的时候形成一个凹槽,然后计算能够装的雨水的体积是多少。
如果遇到相同高度的柱子,这时我们需要保存的是最新的下标,这里需要将原来的栈顶元素pop弹出,然后将当前的下标i放到栈顶中。
如果出现一种情况是当前遍历的高度高于栈顶元素的高度,那么弹出栈顶元素,此时如果栈不为空,则开始计算雨水。此时的栈顶的元素的高度就是凹槽的高度,当前遍历的就是凹槽右边的高度,然后栈顶的下一个元素就是左侧的较高的柱子。right-left-1就是宽度,乘以min(left,right)-height[i]就是最终的面积。
这里详细解释一下面积计算的方法:长×高
长 = 当前遍历的下标位置 - 左侧最高高度下标位置 - 1
高 = min(左侧最高高度,右侧最高高度) - 当前柱子高度,具体体现为当前遍历元素为右侧最高高度,栈顶的元素为凹槽处的高度,栈顶的下一个元素为左侧最高高度。
例如下面这张图中,当我遍历到位置5的时候,其计算其长度应该5-1-1=3,然后高度为min(3,2)-1 = 1,所以面积就是3*1=3。可以看出来这一行的面积确实就是3,符合我们的计算公式。
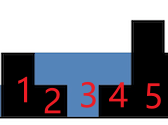
具体的分为下面三种情况:
- 当前遍历的柱子的高度低于栈顶元素的高度,则继续入栈;
- 当前遍历的柱子的高度等于栈顶元素的高度,则将栈顶元素弹出,更新最新柱子高度,将新的柱子下标入栈;
- 当前遍历的柱子的高度大于栈顶元素的高度,此时形成凹槽了,就计算雨水的面积了。
class Solution:def trap(self, height: List[int]) -> int:st = []res = 0for index, h in enumerate(height):while st and height[st[-1]] < h:j = st.pop()if st:res += (index - st[-1] - 1) * (min(h, height[st[-1]]) - height[j])if st and height[st[-1]] == h:st.pop()st.append(index)return res
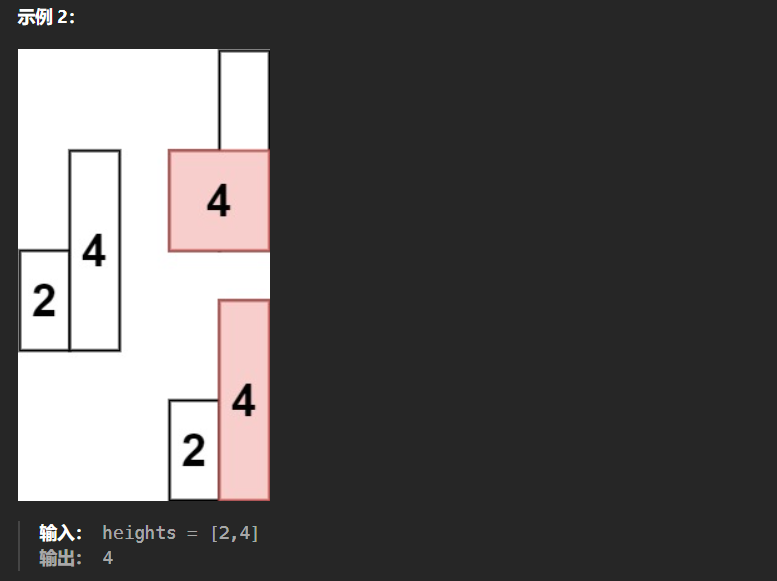
84、柱状图中最大的矩形


在暴力解法中,从每个下标i位置出发,找到左右两侧比其高的位置,但是一旦出现比其低的位置直接break,记录下左右下边left和right,然后用right-left-1作为底面宽度,height[i]作为高度,得到最终的面积。将这个面积与sum_进行比较,取两者中的最大值。
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:# 暴力解法sum_ = 0for i in range(len(heights)):left, right = i, iwhile left >= 0:if heights[left] < heights[i]:breakleft -= 1while right < len(heights):if heights[right] < heights[i]:breakright += 1sum_ = max(sum_, (right - left - 1) * heights[i])return sum_
记录每个柱子左边的第一个小于该柱子的下标,而不是记录左边第一个小于该柱子的高度
双指针的难点就在于如何去寻找当前位置i的左右两侧第一个比其低的柱子的下标
此部分的代码如下:
这里在寻找的时候需要进行初始化,不然的话while循环可能死循环。
注意这里如果minLeftIndex数组中元素值为-1或者minRightIndex数组中元素值为len(heights)表示该柱子左边或者右边没有比其更矮的柱子,此时就以这个柱子的高度乘以宽度即可。
minLeftIndex[0] = -1
for i in range(1,n):t = i-1while t>=0 and heights[t]>=heights[i]:t = minLeftIndex[t] # 左移minLeftIndex[i] = t
# print(minLeftIndex)
minRightIndex[n-1] = n
for i in range(n-2,-1,-1):t = i+1while t<=n-1 and heights[t]>=heights[i]:t = minRightIndex[t]minRightIndex[i] = t
完整代码如下:
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:# 双指针法n = len(heights)minLeftIndex = [0]*nminRightIndex = [0]*n# 寻找左边的小于他的下标minLeftIndex[0] = -1for i in range(1,n):t = i-1while t>=0 and heights[t]>=heights[i]:t = minLeftIndex[t] # 左移minLeftIndex[i] = t# print(minLeftIndex)minRightIndex[n-1] = nfor i in range(n-2,-1,-1):t = i+1while t<=n-1 and heights[t]>=heights[i]:t = minRightIndex[t]minRightIndex[i] = t# print(minRightIndex)res = 0for i in range(n):res = max(res,(minRightIndex[i]-minLeftIndex[i]-1)*heights[i])return res
在接雨水一题中,我们想要实现的效果是寻找到一个凹槽,即找到一个柱子左右两侧高于该柱子的柱子,然后逐行求面积。而本题所需要实现的效果是寻找一个柱子左右两侧低于该柱子的柱子。
单调栈中的顺序(从栈顶到栈底)应该是从大到小的。这样就方便找到每个节点的左边或者右边低于其高度的柱子。当遍历到下一个柱子的高度小于栈顶元素的时候,就可以进行弹出了。在弹出的时候计算高度即可得到最终的答案。
本质上这道题跟接雨水差不多,都可以分成如下三种情况:
- 情况1:当前遍历的元素
height[i]大于栈顶元素height[st[-1]],此时需要入栈 - 情况2:当前遍历的元素
height[i]等于栈顶元素height[st[-1]],此时需要将栈顶元素弹出,然后更新最新的柱子高度对应的下标 - 情况3:当前遍历的元素
height[i]小于栈顶元素height[st[-1]],此时可以进行面积的计算了
计算面积的时候,高度是中间的高度
本题还有一个需要注意的细节,就是需要再heights数组的开头和结尾加上一个0元素,这是因为:
如果数组原本就是一个升序的,如[1,2,3,4,5],进入栈中变成[5,4,3,2,1],就不会走情况3,进行面积的计算,所以需要在最后加上0,强制让其进行结果的计算
如果数组原本就是一个降序的,如[5,4,3,2,1],进入栈中,就会导致无法计算面积,因为目前栈中还是空的。
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:# 单调栈heights.insert(0,0)heights.append(0)stack = [0]res = 0for i in range(1,len(heights)):if heights[i]>heights[stack[-1]]:stack.append(i)elif heights[i]==heights[stack[-1]]:stack.pop()stack.append(i)else:while stack and heights[i] < heights[stack[-1]]:mid = stack.pop()if stack:left_index = stack[-1]right_index = iwidth = right_index - left_index - 1height = heights[mid]res = max(res,width*height)stack.append(i)return res
优化版本:
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:heights.append(0)heights.insert(0,0)st = []res = 0for index,h in enumerate(heights):while st and h<heights[st[-1]]:# 开始进行计算面积mid = st.pop()if st:left = st[-1]right = indexres = max(res,heights[mid]*(right-left-1))if st and heights[st[-1]]==h:st.pop()st.append(index)return res
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:heights.insert(0, 0)heights.append(0)# print(heights)st = []res = 0for index in range(len(heights)):while st and heights[st[-1]] > heights[index]:# 计算面积j = st.pop()if st:res = max(res, (index - st[-1] - 1) * heights[j])if st and heights[st[-1]] == heights[index]:st.pop()st.append(index)return res
1944、队列中可以看到的人数
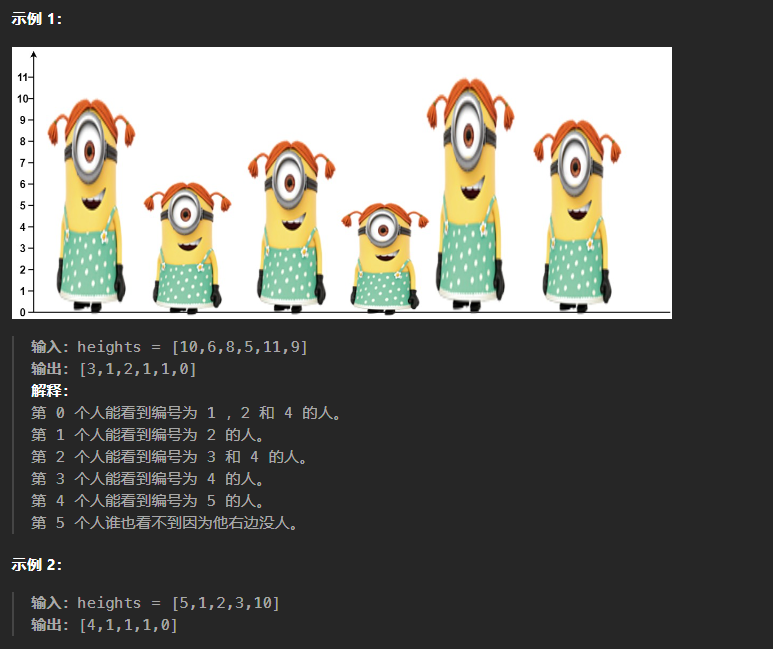

题目解析:本题需要计算一个人能看到其右边的人的人数,如果两个人中间还有其他人,并且前一个人的高度高于后一个人的高度,则后面这个人是无法被看见的。
单调栈的本质:及时去掉没有用的数据。
本题单调栈中存放的是人的高度,并且单调栈中的元素从栈顶到栈底是一个递增的顺序。
本题不是采取的从前往后进行遍历的方式,这样的遍历方式无法避免掉被阻挡掉的矮个子;因此需要从后往前进行遍历,如果当前人的高度比栈中的人的高度高,则栈中元素弹出,并且当前人可以看到的人数加1,同时如果栈不为空的情况,当前的人还可以看到一个人需要加1,然后将当前人的高度入栈。
class Solution:def canSeePersonsCount(self, heights: List[int]) -> List[int]:n = len(heights)ans = [0]*nst = []for i in range(n-1,-1,-1):while st and st[-1]<heights[i]:st.pop()ans[i]+=1if st:ans[i]+=1st.append(heights[i])return ans
相关文章:

【LeetCode】单调栈类题目详解
所有题目均来自于LeetCode,刷题代码使用的Python3版本 单调栈 通常针对一维数组的问题,如果需要寻找一个元素右边或者左边第一个比自己大或者小的元素的位置,就可以使用单调栈,时间复杂度为O(n) 单调栈的本质是空间换时间&#…...

Python上解决TypeError: not all arguments converted during string formatting错误
目录 背景尝试1: pymysql模块的escape_string方法尝试2: 修改pandas.read_excel引擎尝试3: 回退xlrd版本总结 背景 在Linux上部署的时候, 使用pandas模块读取Excel, 然后pymysql模块入库, 结果发生了错误 Traceback (most recent call last):File "/usr/local/lib64/pyth…...

ASUS华硕ROG幻16Air笔记本电脑GU605M原装出厂Win11系统工厂包下载,带有ASUSRecovery一键重置还原
适用型号:GU605MI、GU605MY、GU605MZ、GU605MV、GU605MU 链接:https://pan.baidu.com/s/1YBmZZbTKpIu883jYCS9KfA?pwd9jd4 提取码:9jd4 华硕原厂Windows11系统带有ASUS RECOVERY恢复功能、自带所有驱动、出厂主题壁纸、系统属性联机支持…...

【OpenVINO™】使用 OpenVINO™ C# API 部署 YOLOv9 目标检测和实例分割模型(上篇)
YOLOv9模型是YOLO系列实时目标检测算法中的最新版本,代表着该系列在准确性、速度和效率方面的又一次重大飞跃。它通过引入先进的深度学习技术和创新的架构设计,如通用ELAN(GELAN)和可编程梯度信息(PGI)&…...

代码随想录——二分查找(一)
模版 func BinarySearch(nums *int,target int){l,r:0,len(nums)-1for l<r{mid:l(r-l)/2if nums[mid]target{return mid}else if nums[mid]<target{lmid1}else{rmid-1}}return -1 }特点 查找条件可以在不与元素的两侧进行比较的情况下确定(或使用它周围的特…...
【NLP】多标签分类【下】
文章目录 简介个人博客与相关链接1 实验数据与任务说明2 模型介绍2.1 TransformerTransformer能做什么? 2.2 Hugging FaceHugging Face的Transformers库社区支持和资源预训练模型的应用 2.3 T5模型(Text-To-Text Transfer Transformer)T5的核…...

HWOD:密码强度等级
一、知识点 回车键的ASCII码是10 如果使用EOF,有些用例不通过 二、题目 1、描述 密码按如下规则进行计分,并根据不同的得分为密码进行安全等级划分。 一、密码长度: 5 分: 小于等于4 个字符 10 分: 5 到7 字符 25 分: 大于等于8 个字符 二、字母: 0…...

期货学习笔记-MACD指标学习2
MACD底背离把握买入多单的技巧 底背离的概念及特征 底背离指的是MACD指标与价格低点之间的对比关系,这里需要明白的是MACD指标的涨跌动能和价格形态衰竭形态之间的关系,如果市场价格创新低而出现衰竭形态同时也有底背离形态的出现,此时下跌…...

5G智慧港口简介(一)
引言 港口作为交通运输的枢纽,在促进国际贸易和地区发展中起着举足轻重的作用,全球贸易中约 90% 的贸易由海运业承载,作业效率对于港口至关重要。在“工业 4.0”、“互联网 +”大发展的时代背景下,港口也在进行数字化、全自动的转型升级。随着全球 5G 技术浪潮的到来,华为…...
订单中台架构:打造高效订单管理系统的关键
在现代商业环境下,订单管理对于企业来说是至关重要的一环。然而,随着业务规模的扩大和多渠道销售的普及,传统的订单管理方式往往面临着诸多挑战,如订单流程复杂、信息孤岛、数据不一致等问题。为了应对这些挑战并抓住订单管理的机…...
【算法】模拟
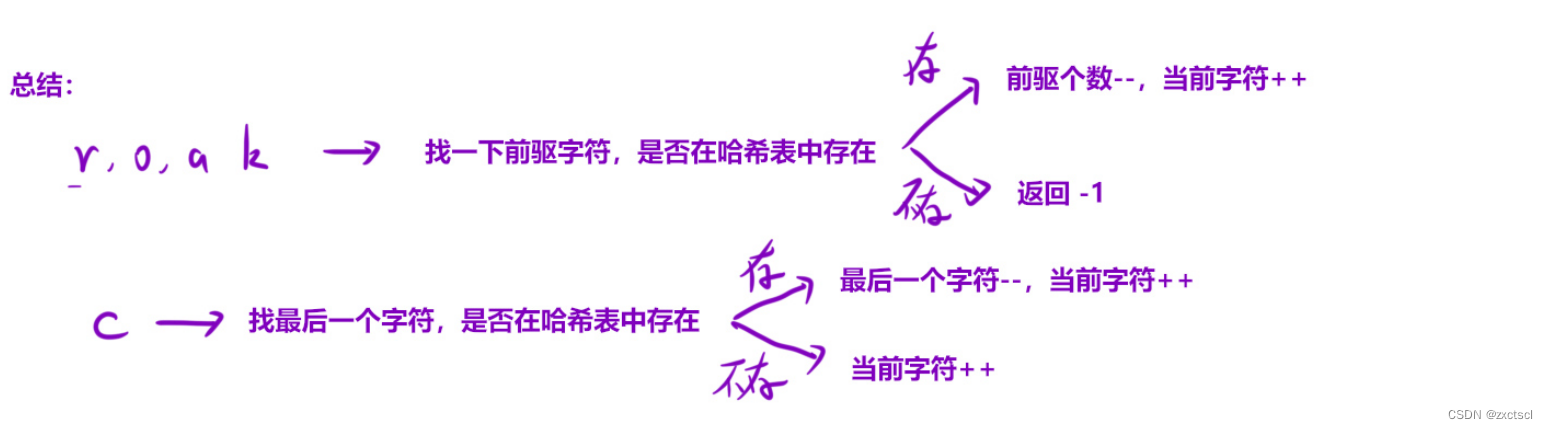
个人主页 : zxctscl 如有转载请先通知 题目 前言1. 1576. 替换所有的问号1.1 分析1.2 代码 2. 495. 提莫攻击2.1 分析2.2 代码 3. 6. Z 字形变换3.1 分析3.2 代码 4. 38. 外观数列4.1 分析4.2 代码 5. 1419. 数青蛙5.1 分析5.2 代码 前言 模拟算法就是根据题目所给…...

电力综合自动化系统对电力储能技术的影响有哪些?
电力综合自动化系统对电力储能技术的影响主要体现在以下几个方面: 提高能源利用效率:电力综合自动化系统通过优化调度和能量管理,可以实现储能设备的有效利用,提高能源利用效率。在电力系统中,储能设备可以有效地平抑风…...

Compose UI 之 Card 卡片组件
Card Card 是用于显示带有圆角和可选阴影的矩形内容容器。它通常用于构建用户界面,并可以包含标题、文本、图像、按钮等元素,表示界面上的可交互元素,我们称它是 “卡片”。 Card 使用的一些经典的场景: 列表数据,例如 新闻列表,产品列表等。信息提示框,使用 Card 组件…...
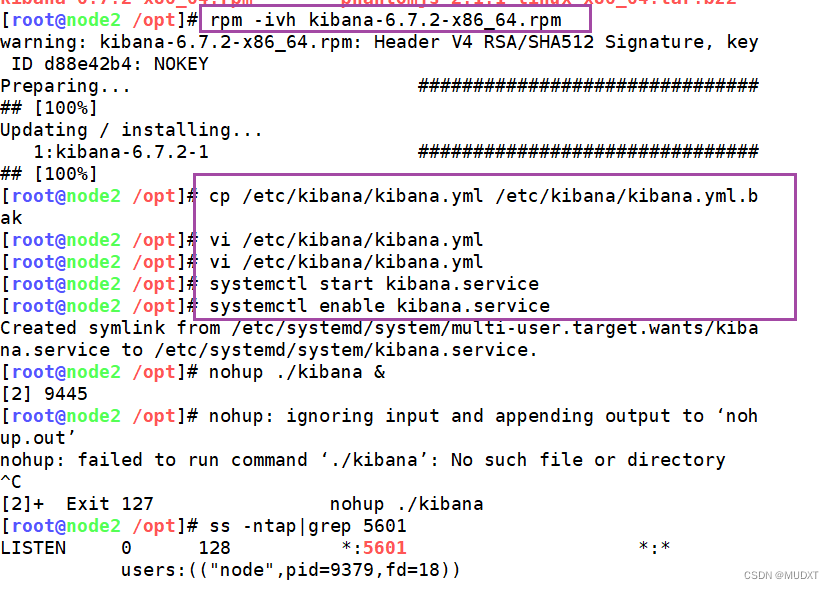
ELK日志
...

WPF Pack
在WPF中,Pack URI(Uniform Resource Identifier)是一种特殊格式的统一资源标识符,用于定位和访问应用程序内部或外部的各种资源,如XAML文件、图像、样式、字体等。这种机制允许开发者以标准化、平台无关的方式引用和打…...

计算两个时间段的差值
计算两个时间段的差值 运行效果: 代码实现: #include<stdio.h>typedef struct {int h; // 时int m; // 分int s; // 秒 }Time;void fun(Time T[2], Time& diff) {int sum_s[2] { 0 }; for (int i 0; i < 1; i) { // 统一为秒数sum_s[…...
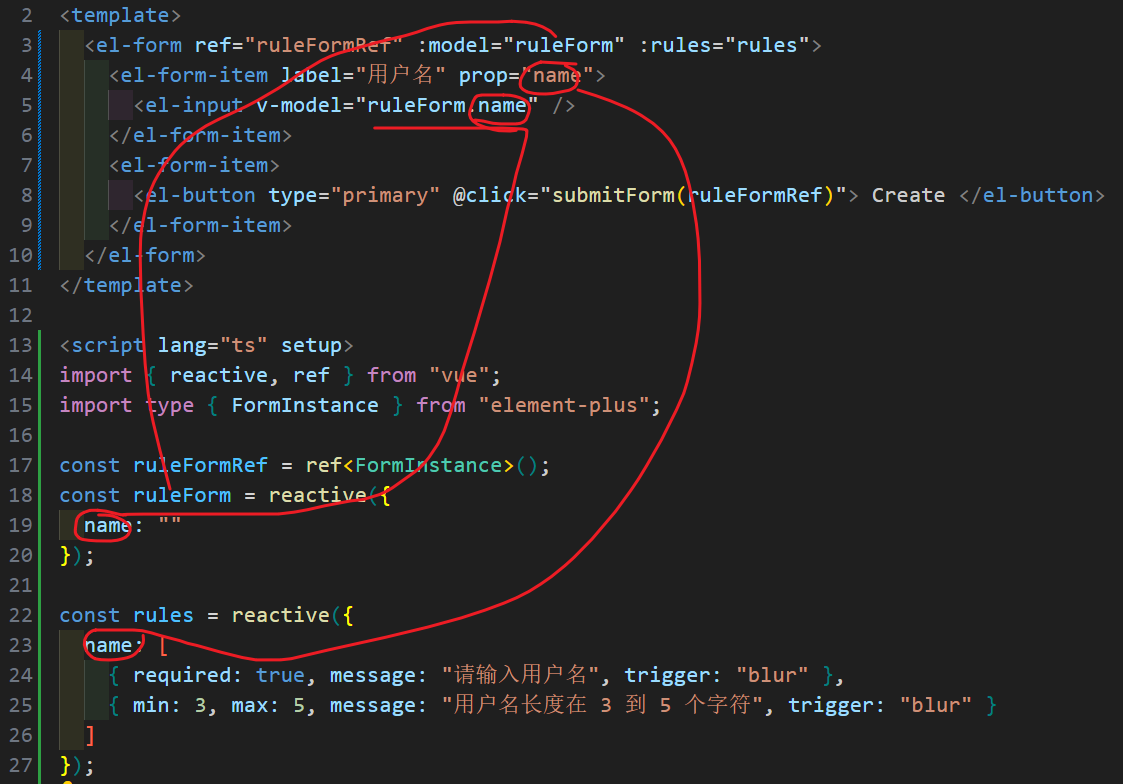
Element Plus 表单校验
原理 为 rules 属性传入约定的验证规则,并将 form-Item 的 prop 属性设置为需要验证的特殊键值:model和:rules中字段的名称需要一致 示例: <template><el-form ref"ruleFormRef" :model"ruleForm" :rules"rules&q…...
java实现TCP交互
服务器端 import java.io.IOException; import java.io.InputStream; import java.io.OutputStream; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Socket; import java.util.PriorityQueue; import java.util.Scanner;public class TCP_Serv…...

学习云计算HCIE选择誉天有什么优势?
誉天云计算课程优势实战性强 课程注重实践操作,通过实际案例和实验操作,让学员深入了解云计算的应用场景和实际操作技能。课程内容全面 涵盖所有云计算涉及的IT基础知识、服务器、存储、网络等方面的基础知识,开源操作系统Linux,开…...
python之文件操作与管理
1、文件操作 通过open()操作,来创建文件对象,下面是open()函数语法如下: open(file,mode r,buffering -1 , encoding None ,errors None , newline None,closefd True,opener …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
