(Java)数据结构——图(第七节)Folyd实现多源最短路径
前言
本博客是博主用于复习数据结构以及算法的博客,如果疏忽出现错误,还望各位指正。
Folyd实现原理
中心点的概念
感觉像是充当一个桥梁的作用
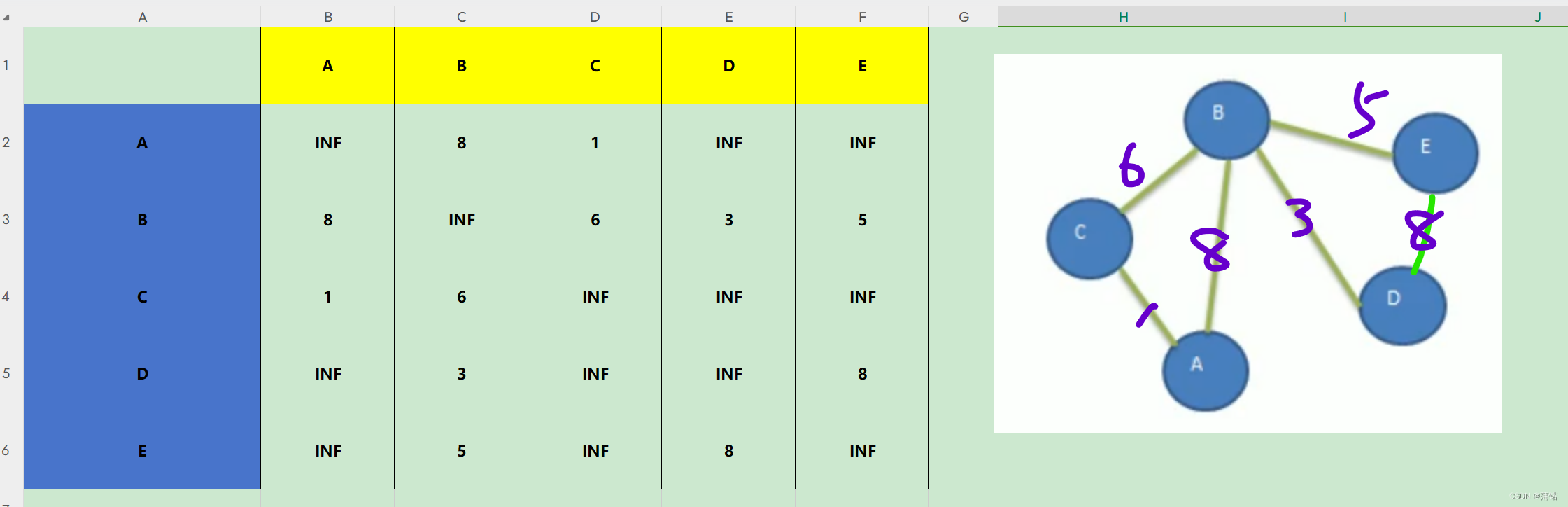
还是这个图
我们常在一些讲解视频中看到,就比如dist(-1),这是原始的邻接矩阵
dist(0),就是A充当中心点
这时候就是打比方,我D->E,A作为中心点之后,这一轮就是看D->A->E的距离相较之前是否最小,所以,A->A->B多次一举,所以pass,X->A->A也是多此一举,所以pass,对角线别动X->A->X又回到自己PASS。一来三个pass,差不多如图。我们只需要剩下的就可以。
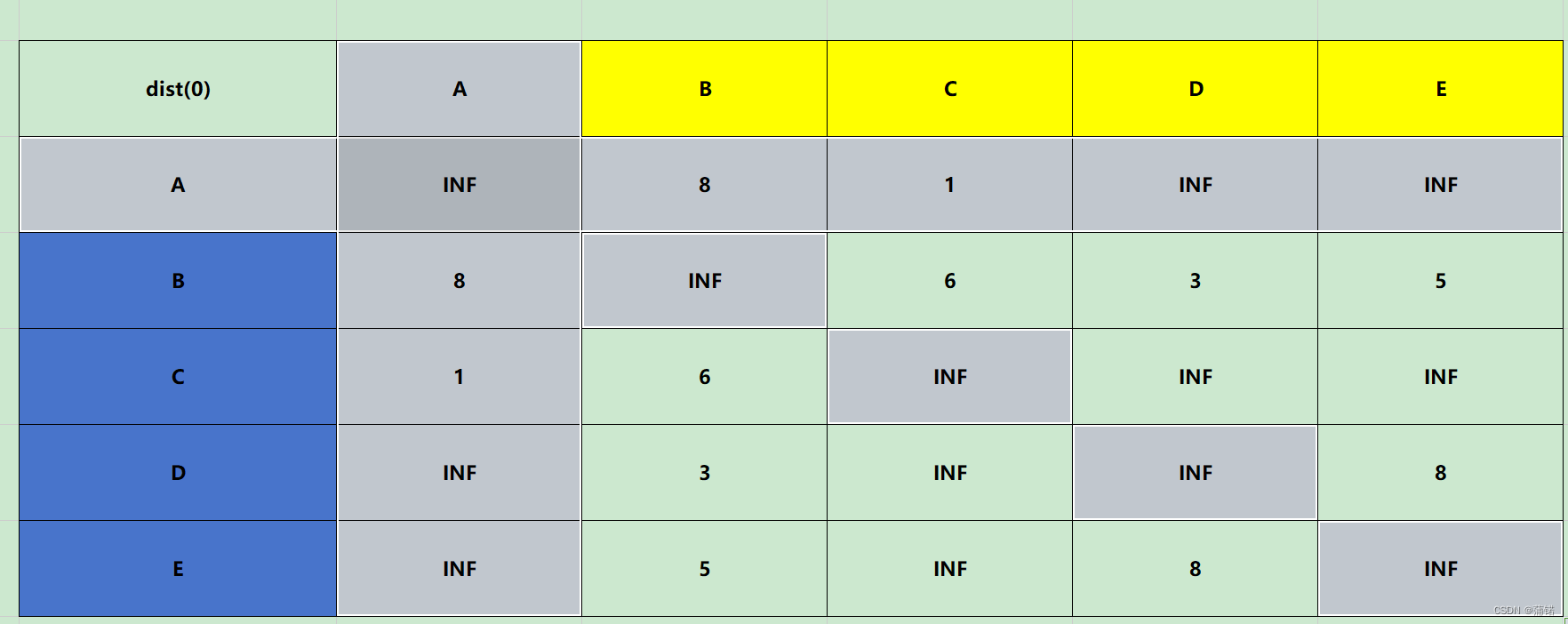
打比方B->C,那么加入A之后就是B->A->C=BA+AC=8+1=9,相比于之前的6,大了,所以不换不更新。
B->E,那么加入A之后就是B->A->E,BA+AE=8+INF,直接pass遇到不通的情况。
遍历完B,到C继续重复步骤更新……即可,脑力有限,就不多解释了。
这样我每个点都充当一次中心点下来,我的最短路径也出来了。
Folyd实现代码
Folyd的代码形式十分简单,如果比赛中看寻找最短路径,嫌Dijkstra算法麻烦的话,直接试试Folyd看看能不能过,不能再说单源的。以下是主要实现代码。
public int[][] Folyd(){int N = vertexList.size();int[][] edges = new int[N][N];//新开个二维数组,防止数据被动//edges[i] = this.edges[i],这样是不行的,因为java的引用for(int i = 0;i<N;i++){for(int j=0;j<N;j++){edges[i][j] = this.edges[i][j];}}//弗洛伊德算法就是要求整个的for(int k = 0;k<N;k++){//中心点for(int i = 0;i<N;i++){//哪个点//if(i==k) continue;for(int j = 0;j<N;j++){//到哪个点//if(j == k) continue;if(i == j) continue;if(edges[i][k] !=Integer.MAX_VALUE && edges[k][j] != Integer.MAX_VALUE){edges[i][j] = Math.min(edges[i][j], edges[i][k] + edges[k][j]);//当前的ij位置}}}}return edges;}三层循环,代码中注释//掉的if就是我原理里面pass的东西。
以下是完整的实现代码,以及与迪杰斯特拉算法结果的比对。
//package GraphTest.Demo;import java.util.*;public class Graph{//这是一个图类/***基础属性***/int[][] edges; //邻接矩阵存储边ArrayList<EData> to = new ArrayList<>(); //EData包含start,end,weight三个属性,相当于另一种存储方式,主要是为了实现kruskal算法定义的ArrayList<String> vertexList = new ArrayList<>(); //存储结点名称,当然你若想用Integer也可以,这个是我自己复习用的int numOfEdges; //边的个数boolean[] isVisited;//构造器Graph(int n){this.edges = new int[n][n];//为了方便,决定讲结点初始化为INF,这也方便后续某些操作int INF = Integer.MAX_VALUE;for(int i=0;i<n;i++){Arrays.fill(edges[i],INF);}this.numOfEdges = 0;this.isVisited = new boolean[n];}//插入点public void insertVertex(String vertex){//看自己个人喜好,我这边是一个一个在主方法里插入点的名称vertexList.add(vertex);}//点的个数public int getNumOfVertex(){return vertexList.size();}//获取第i个节点的名称public String getVertexByIndex(int i){return vertexList.get(i);}//获取该节点的下标public int getIndexOfVertex(String vertex){return vertexList.indexOf(vertex);}//插入边public void insertEdge(int v1,int v2,int weight){//注意,这里是无向图edges[v1][v2] = weight;edges[v2][v1] = weight;this.numOfEdges++;//如果要用Kruskal算法的话这里+to.add(new EData(v1,v2,weight)); //加入from to这种存储方式}//边的个数public int getNumOfEdge(){return this.numOfEdges;}//得到点到点的权值public int getWeight(int v1,int v2){//获取v1和v2边的权重return edges[v1][v2];}//打印图public void showGraph(){for(int[] line:edges){System.out.println(Arrays.toString(line));}}//获取index行 第一个邻接结点public int getFirstNeighbor(int index){for(int i = 0;i < vertexList.size();i++){if(edges[index][i] != Integer.MAX_VALUE){return i; //找到就返回邻接结点的坐标}}return -1; //没找到的话,返回-1}//获取row行 column列之后的第一个邻接结点public int getNextNeighbor(int row,int column){for(int i = column + 1;i < vertexList.size();i++){if(edges[row][i] != Integer.MAX_VALUE){return i; //找到就返回邻接结点的坐标}}return -1; //没找到的话,返回-1}//DFS实现,先定义一个isVisited布尔数组确认该点是否遍历过public void DFS(int index,boolean[] isVisited){System.out.print(getVertexByIndex(index)+" "); //打印当前结点isVisited[index] = true;//查找index的第一个邻接结点fint f = getFirstNeighbor(index);//while(f != -1){//说明有if(!isVisited[f]){//f没被访问过DFS(f,isVisited); //就进入该节点f进行遍历}//如果f已经被访问过,从当前 i 行的 f列 处往后找f = getNextNeighbor(index,f);}}//考虑到连通分量,需要对所有结点进行一次遍历,因为有Visited,所以不用考虑冲突情况public void DFS(){for(int i=0;i<vertexList.size();i++){if(!isVisited[i]){DFS(i,isVisited);}}}public void BFS(int index,boolean[] isVisited){//BFS是由队列实现的,所以我们先创建一个队列LinkedList<Integer> queue = new LinkedList<>();System.out.print(getVertexByIndex(index)+" "); //打印当前结点isVisited[index] =true; //遍历标志turequeue.addLast(index); //队尾加入元素int cur,neighbor; //队列头节点cur和邻接结点neighborwhile(!queue.isEmpty()){//如果队列不为空的话,就一直进行下去//取出队列头结点下标cur = queue.removeFirst(); //可以用作出队//得到第一个邻接结点的下标neighbor = getFirstNeighbor(cur);//之后遍历下一个while(neighbor != -1){//邻接结点存在//是否访问过if(!isVisited[neighbor]){System.out.print(getVertexByIndex(neighbor)+" ");isVisited[neighbor] = true;queue.addLast(neighbor);}//在cur行找neighbor列之后的下一个邻接结点neighbor = getNextNeighbor(cur,neighbor);}}}//考虑到连通分量,需要对所有结点进行一次遍历,因为有Visited,所以不用考虑冲突情况public void BFS(){for(int i=0;i<vertexList.size();i++){if(!isVisited[i]){BFS(i,isVisited);}}}public void prim(int begin){//Prim原理:从当前集合选出权重最小的邻接结点加入集合,构成新的集合,重复步骤,直到N-1条边int N = vertexList.size();//当前的集合 与其他邻接结点的最小值int[] lowcost = edges[begin];//记录该结点是从哪个邻接结点过来的int[] adjvex = new int[N];Arrays.fill(adjvex,begin);//表示已经遍历过了,isVisited置trueisVisited[begin] = true;for(int i =0;i<N-1;i++){//进行N-1次即可,因为只需要联通N-1条边//寻找当前集合最小权重邻接结点的操作int index = 0;int mincost = Integer.MAX_VALUE;for(int j = 0;j<N;j++){if(isVisited[j]) continue;if(lowcost[j] < mincost){//寻找当前松弛点mincost = lowcost[j];index = j;}}System.out.println("选择节点"+index+"权重为:"+mincost);isVisited[index] = true;System.out.println(index);//加入集合后更新的操作,看最小邻接结点是否更改for(int k = 0;k<N;k++){if(isVisited[k]) continue;//如果遍历过就跳过if(edges[index][k] < lowcost[k]){ //加入新的节点之后更新,检查原图的index节点,加入后,是否有更新的lowcost[k] = (edges[index][k]);adjvex[k] = index;}}}}//用于对之前定义的to进行排序public void toSort(){Collections.sort(this.to, new Comparator<EData>() {@Overridepublic int compare(EData o1, EData o2) {//顺序对就是升序,顺序不对就是降序,比如我现在是o1和o2传进来,比较时候o1在前就是升序,o1在后就是降序int result = Integer.compare(o1.weight,o2.weight);return result;}});}//并查集查找public int find(int x,int[] f){while(x!=f[x]){x = f[x];}return x;}//并查集合并public int union(int x,int y,int[] f){find(x,f);find(y,f);if(x!=y){f[x] = y;return y;}return -1; //如果一样的集合就返回-1}public ArrayList<Integer> kruskal(){//kruskal是对form to weight这种结构的类进行排序,然后选取最短的一条边,看是否形成回路,加入toSort(); //调用toSort进行排序//由于要判断是否形成回路,我们可以用DFS或者BFS,因为之前都写过,所以我们在这用并查集//初始化并查集int[] f = new int[vertexList.size()];for(int i = 0;i<vertexList.size();i++){f[i] = i;}ArrayList<Integer> res = new ArrayList<>();int count = 0;for(int i = 0;count != vertexList.size()-1 && i<this.to.size();i++){//之后就是开始取边了EData temp = this.to.get(i);if(union(temp.start,temp.end,f)!=-1){//如果查到不是一个集,就可以添加//这里都加进来是方便看哪个边res.add(temp.start);res.add(temp.end);count++;}}return res; //最后把集合返回去就行}public int[] Dijkstra(int begin){int N = vertexList.size();//到其他点的最短路径,动态更新,直到最后返回int[] dist = new int[N];for(int i=0;i<N;i++){ //进行一下拷贝,以免更改核心数据dist[i] = edges[begin][i];}//System.out.println(Arrays.toString(dist));isVisited[begin] = true; //该点已经遍历过int[] path = new int[N]; //记录这个点从哪来的,到时候在path里寻找就行//比如path 2 1 1 1 1,那么A就是从C来的,然后去C,C是从B来的,B是从B来的,OK结束,路径出来Arrays.fill(path,begin);for(int i = 0;i<N;i++){//几个点遍历多少次int min = Integer.MAX_VALUE;int index = 0;for(int j = 0;j<N;j++){//寻找当前的最短路径if(!isVisited[j]){if(dist[j] < min){min = dist[j];index = j;}}}isVisited[index] = true; //置为遍历过for(int k = 0;k<N;k++){//新加入点后,看min+edges[新加点的那一行],看是不是比以前的小,小就换了if(!isVisited[k] && edges[index][k]!=Integer.MAX_VALUE){//此处格外注意,因为Integer.MAX_VALUE再+就变成负的了,所以一定要注意if(dist[index]+edges[index][k] < dist[k]){dist[k] = dist[index]+edges[index][k];path[k] = index;}}}//找到了之后呢}//System.out.println(Arrays.toString(dist));//System.out.println(Arrays.toString(path));return dist; //返回的是到每个点的最小路径}public int[][] Folyd(){int N = vertexList.size();int[][] edges = new int[N][N];for(int i = 0;i<N;i++){for(int j = 0;j<N;j++){edges[i][j] = this.edges[i][j];}}//弗洛伊德算法就是要求整个的for(int k = 0;k<N;k++){//中心点for(int i = 0;i<N;i++){//哪个点//if(i==k) continue;for(int j = 0;j<N;j++){//到哪个点//if(j == k) continue;if(i == j) continue;if(edges[i][k] !=Integer.MAX_VALUE && edges[k][j] != Integer.MAX_VALUE){edges[i][j] = Math.min(edges[i][j], edges[i][k] + edges[k][j]);//当前的ij位置}}}}return edges;}public static void main(String[] args) {int n = 5;String[] Vertexs ={"A","B","C","D","E"};//创建图对象Graph graph = new Graph(n);for(String value:Vertexs){graph.insertVertex(value);}graph.insertEdge(0,1,8);graph.insertEdge(0,2,1);graph.insertEdge(1,2,6);graph.insertEdge(1,3,3);graph.insertEdge(1,4,5);graph.insertEdge(3,4,8);
// graph.showGraph();
//
// graph.DFS(1, graph.isVisited);
// System.out.println();
// graph.DFS();//再求求所有的,看有没有剩下的
// System.out.println();
// Arrays.fill(graph.isVisited,false);
// graph.BFS(1, graph.isVisited);
// System.out.println();
// Arrays.fill(graph.isVisited,false);
// graph.BFS();
// System.out.println();
// Arrays.fill(graph.isVisited,false);
// graph.prim(2);
// graph.toSort();
// for(EData i : graph.to){
// System.out.println(i.toString());
// }
// System.out.println(graph.kruskal().toString());;
// Arrays.fill(graph.isVisited,false);for(int i = 0;i<graph.getNumOfVertex();i++){//每个点的到其他点的最短路径只需要遍历一遍即可,时间复杂度On3Arrays.fill(graph.isVisited,false);System.out.println(Arrays.toString(graph.Dijkstra(i)));;}for(int[] i : graph.Folyd()){System.out.println(Arrays.toString(i));}}
}class EData{//当然,这是为了方便,直接记录结点下标,而不记录像"A"这种int start;int end;int weight;EData(int start,int end,int weight){this.start = start;this.end = end;this.weight = weight;}@Overridepublic String toString() {return "EData{" +"start=" + start +", end=" + end +", weight=" + weight +'}';}
}
相关文章:

(Java)数据结构——图(第七节)Folyd实现多源最短路径
前言 本博客是博主用于复习数据结构以及算法的博客,如果疏忽出现错误,还望各位指正。 Folyd实现原理 中心点的概念 感觉像是充当一个桥梁的作用 还是这个图 我们常在一些讲解视频中看到,就比如dist(-1)࿰…...

使用Python进行高效的多线程HTTP请求
在处理网络请求时,尤其是当需要大量请求相同或不同的URL时,采用多线程的方式可以显著提高效率。本文介绍了如何使用Python的concurrent.futures模块实现多线程HTTP请求。 为什么使用多线程? 多线程可以让CPU和网络资源得到更有效的利用。在…...

如何利用OceanBase v4.2的 外部表简化外部数据处理
为什么需要使用外表 在日常的业务场景中,经常遇到需要在数据库中处理外部数据的情况,这些数据可能来源于应用程序,或者是其他业务系统。一般来说,常是通过ETL工具将外部数据库的数据导入到数据库内部的表中,再进行分析…...
【灵境矩阵】零代码创建AI智能体之行业词句助手
欢迎来到《小5讲堂》 这是《灵境矩阵》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 目录 创建智能体选择创建方式零代码 基础配置头像名称简介指令开场白…...

springboot 防抖操作
大佬的代码:看这里 原理: 通过aop切面编程,在调用接口前缓存接口信息,将信息缓存到redis中,在规定时间内重复调用接口,会被拦截请求 有个地方感觉不太合理,在使用中我将其修改了 //前略 publi…...

Playwright录制脚本 —— web自动化测试!
简介: 在编写 web 自动化测试用例时,代码编写的速度是否快,会影响框架的使用体验。现在很多的框架都会提供一些辅助功能,帮助我们更快的去编写自动化测试代码,而录制功能是几乎所有的web自动化工具都会带的功能。在实际…...

什么是工业级物联网智能网关?如何远程控制PLC?
在数字化浪潮席卷全球的今天,工业物联网(IIoT)已经成为推动工业转型升级的关键力量。而在工业物联网的大家庭中,工业级物联网智能网关扮演着举足轻重的角色。那么,究竟什么是工业级物联网智能网关?又该如何…...
:2024.04.05-2024.04.10)
AI推介-大语言模型LLMs论文速览(arXiv方向):2024.04.05-2024.04.10
文章目录~ 1.Learn from Failure: Fine-Tuning LLMs with Trial-and-Error Data for Intuitionistic Propositional Logic Proving2.Continuous Language Model Interpolation for Dynamic and Controllable Text Generation3.Event Grounded Criminal Court View Generation w…...
、apply()、bind()的区别和使用)
javascript:call()、apply()、bind()的区别和使用
javascript:call()、apply()、bind()的区别和使用 1 前言 记录javascript的call、apply、bind方法绑定this的区别以及使用。 call、apply、bind的区别: 【相同点】:作用相同,都是动态修改this指向;都不会修改原先函…...

ubuntu系统安装systemc-2.3.4流程
背景:systemC编程在linux下的基础环境配置 1,下载安装包,并解压 (先下载了最新的3.0.0,安装时候显示sc_cmnhdr.h:115:5: error: #error **** SystemC requires a C compiler version of at least C17 **** ÿ…...

Java开发中的entity、vo和pojo
Java开发中的entity、vo和pojo 1.Entity实体2.vo3.pojo 1.Entity实体 定义: Entity 通常指的是与数据库表对应的对象。它包含了与数据库表字段相对应的属性和一些业务逻辑方法。Entity 通常用于数据的持久化操作,如增删改查。使用场景: 当需…...

通过IPV6+DDNS实现路由器远程管理和Win远程桌面控制
前期需要的准备: 软路由,什么系统都可以,要支持IPV6,能够自动添加解析 光猫的管理员账号,能够进入光猫修改配置,拨号上网账号 域名账号和DNS服务 主要步骤: 利用管理员账号,进入…...

数据湖/数据仓库
数据湖(Data Lake)和数据仓库(Data Warehouse)的主要区别在于它们的目的、存储的数据类型、数据处理方式、数据结构、数据安全性以及数据应用。以下是相关介绍: 目的。数据湖旨在作为一个集中的存储库,存储…...

万兆以太网MAC设计(2)MAC_RX模块
文章目录 前言一、模块功能二、代码三、仿真波形 前言 上文我们打通了了万兆以太网物理层和数据链路层,其实就是会使用IP核了,本文将正式开始MAC层设计第一篇,接收端设计。 一、模块功能 MAC_RX模块功能如下: 解析接收的报文&…...
D. Solve The Maze Codeforces Round 648 (Div. 2)
题目链接: Problem - 1365D - CodeforcesCodeforces. Programming competitions and contests, programming communityhttps://codeforces.com/problemset/problem/1365/D 题目大意: 有一张地图n行m列(地图外面全是墙),…...
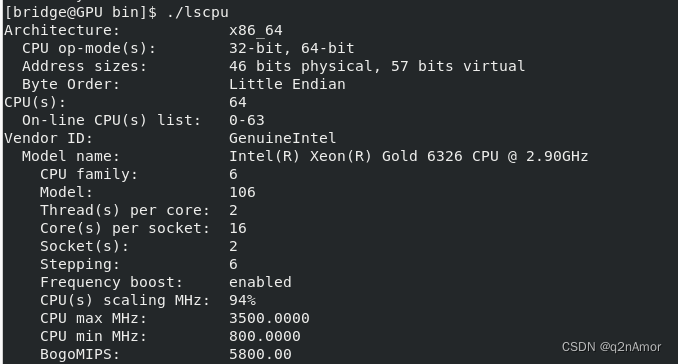
CPU核心数、线程数都是什么意思?
最早,每个物理 cpu 上只有一个核心,对操作系统而言,也就是同一时刻只能运行一个进程/线程。 为了提高性能,cpu 厂商开始在单个物理 cpu 上增加核心(实实在在的硬件存在),也就出现了多核 cpu&…...

每日一篇 4.12
misstep:失误 epic proportions.:史无前例 arguably:按理来说 assembly:组装 performed :执行 underpins:支撑 holds a monopoly:垄断了 shipped:发货 a market capitalizati…...

鸿蒙南向开发:【智能烟感】
样例简介 智能烟感系统通过实时监测环境中烟雾浓度,当烟雾浓度超标时,及时向用户发出警报。在连接网络后,配合数字管家应用,用户可以远程配置智能烟感系统的报警阈值,远程接收智能烟感系统报警信息。实现对危险及时报…...

【主题广|检索稳定】2024年生态工程与农业科技国际会议 (EEAT 2024)
2024年生态工程与农业科技国际会议 (EEAT 2024) 2024 International Conference on Ecological Engineering and Agricultural Technology 【会议简介】 2024年生态工程与农业科技国际会议即将在贵阳召开。本次会议将汇集全球生态工程与农业科技领域的专家学者,共…...

代码随想录算法训练营第三十八天|509. 斐波那契数、 70. 爬楼梯、746. 使用最小花费爬楼梯
509 题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
