一些优雅的算法(c++)
求最大公约数:辗转相除法
int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}
求最小公倍数:两整数之积除以最大公约数
int lcm(int a, int b){return a*b / gcd(a, b);
}
十进制转n进制:
char get(int x){if(x<=9){return x+'0';}else{return (x-10)+'A';}
}
string base(int x) // 十进制转 n进制
{string num;while(x){num += get(x % n), x /= n;}reverse(num.begin(),num.end());return num;
}
c语言输出
printf("%02d", a)
表示输出按俩位输出整形a,比如a=8,则输出08,a=24,输出24
printf("%.2f",a)
表示输出浮点数a小数点后俩位,比如a=8,则输出8.00,a=1.123,则输出a=1.12
最短路径问题

什么是链式前向星实现邻接表
链式前向星实现:设置三个数组,一个数组h用来存节点,一个数组e用来存值,一个数组ne用来存下一个节点。我们需要设置索引idx来实现ne的查找,不然没法链接起来
void add(int a,int b) {
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
例:
 我们遍历的话就是从h[1]开始遍历,此时h[1]=4,然后我们找下一个节点,下一个节点对应的索引就是3,再下一个节点对应的索引就是0,当索引为-1时结束。这个过程next实际上是向前走的,关系又是链式的,因此成为链式前向星
我们遍历的话就是从h[1]开始遍历,此时h[1]=4,然后我们找下一个节点,下一个节点对应的索引就是3,再下一个节点对应的索引就是0,当索引为-1时结束。这个过程next实际上是向前走的,关系又是链式的,因此成为链式前向星
为什么要用memset(dist,0x3f,sizeof dist)来初始化
回答::0x3f3f3f3f的十进制是1061109567,是1e9级别的(和0x7fffffff一个数量级,0x7fffffff代表了32-bit int的最大值),而一般场合下的数据都是小于1e9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。 另一方面,由于一般的数据都不会大于10^9,所以当我们把无穷大加上一个数据时,它并不会溢出(这就满足了“无穷大加一个有穷的数依然是无穷大”),事实上0x3f3f3f3f+0x3f3f3f3f=2122219134,这非常大但却没有超过32-bit int的表示范围,所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
floyd
E.路径(12届蓝桥杯c++B组第一场省赛)
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图中的最短路径。
小蓝的图由 2021 个结点组成,依次编号 1 至 2021。
对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。
例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为 75。
请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题。
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
const int N = 3000;
int n = 2021;
int g[N][N];
// 求最小公约数
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}void floyb() {for (int t = 1; t <= n; ++ t) {for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {g[i][j] = min(g[i][j], g[i][t] + g[t][j]);}}}
}
int main (){memset(g, 0x3f, sizeof g);for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {if (abs(i - j) <= 21) {// 最大公倍数求法g[i][j] = i * j / gcd(i, j);}}}floyb();cout << g[1][n] << endl;return 0;
}
并查集
小蓝要用七段码数码管来表示一种特殊的文字。

上图给出了七段码数码管的一个图示,数码管中一共有 7 段可以发光的二 极管,分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符 的表达时,要求所有发光的二极管是连成一片的。
例如: b 发光,其他二极管不发光可以用来表达一种字符。
例如: c 发光,其他二极管不发光可以用来表达一种字符。这种 方案与上 一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如: a, b, c, d, e 发光, f, g 不发光可以用来表达一种字符。
例如: b, f 发光,其他二极管不发光则不能用来表达一种字符,因为发光 的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include<bits/stdc++.h>
using namespace std;
const int N=10;
int e[N][N],use[N],ans=0,fa[N];
int find(int f){//查找父值 if(fa[f]==f){return f;}return find(fa[f]);
}
void dfs(int n){if(n>7){for(int i=1;i<=7;i++){fa[i]=i;//每个元素单独成一个集合 }for(int i=1;i<=7;i++){//遍历每条边 for(int j=1;j<=7;j++){if(e[i][j]&&use[i]&&use[j]){//如果ij连通且都已打开,使它们的父集相等 int fx=find(i),fy=find(j);if(fx!=fy){fa[fx]=fy;//合并集合:即让它们的父值相等 }}}}int k=0;for(int i=1;i<=7;i++){ if(fa[i]==i&&use[i]){//判断现有元素有几个集合 k++;}}if(k==1){//如果已使用的灯在一个集合内:即父集只有一个元素 ans++;}return ;}use[n]=1;dfs(n+1);use[n]=0;dfs(n+1);
}
int main(){e[1][2]=e[1][6]=1;e[2][3]=e[2][7]=1;e[3][4]=e[3][7]=1;e[4][5]=1;e[5][6]=e[5][7]=1;e[6][7]=1;dfs(1);cout<<ans<<endl;return 0;
}
getline()
接收一个字符串,可以接收空格并输出,读取缓冲区的回车然后舍弃
#include<iostream>
#include<string>
using namespace std;
main ()
{
string str;
getline(cin,str);
cout<<str<<endl;
}
输入:jkljkljkl
输出:jkljkljkl
输入:jkl jfksldfj jklsjfl
输出:jkl jfksldfj jklsjfl
push_back()
push_back() 在Vector最后添加一个元素(参数为要插入的值)
vector<int> vec;
vec.push_back(10);
//在容器中添加10
或者再string中最后插入一个字符;
string str;
str.push_back('d');
类似的:
pop_back() //移除最后一个元素
clear() //清空所有元素
empty() //判断vector是否为空,如果返回true为空
erase() // 删除指定元素
相关文章:

一些优雅的算法(c++)
求最大公约数:辗转相除法 int gcd(int a,int b){return b0?a:gcd(b,a%b); }求最小公倍数:两整数之积除以最大公约数 int lcm(int a, int b){return a*b / gcd(a, b); }十进制转n进制: char get(int x){if(x<9){return x0;}else{return…...
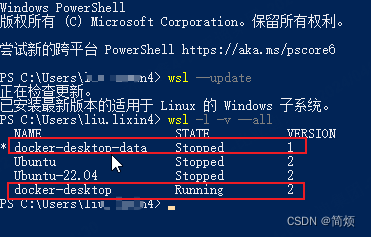
Docker Desktop修改镜像存储路径 Docker Desktop Start ... 卡死
1、CMD执行wsl -l -v --all 2、Clean / Purge data 3、导出wsl子系统镜像: wsl --export docker-desktop D:\docker\wsl\distro\docker-desktop.tar wsl --export docker-desktop-data D:\docker\wsl\data\docker-desktop-data.tar4、删除现有的wsl子系统: wsl -…...

小型企业网络安全指南
许多小型企业刚刚起步,没有大公司所拥有的相同资源来保护其数据。他们不仅可能没有资金来支持多样化的安全计划,而且也可能没有人力或时间。 网络犯罪分子知道小型企业缺乏这些资源,并利用这些资源来谋取利益。遭受网络攻击后,小…...
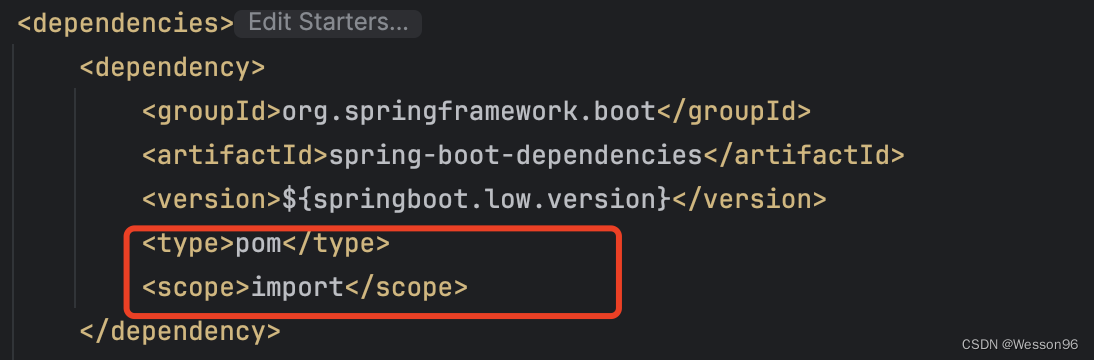
springboot相关报错解决
Caused by: java.lang.ClassNotFoundException: 目录 Caused by: java.lang.ClassNotFoundException: org.springframework.context.event.GenericApplicationListener spring-boot-dependencies:jar:2.1.9.RELEASE was not found org.springframework.context.event.Generi…...

python 中 from import, __name__, __all__, __init__.py 作用,python的模块和导入包
from import 即类似于其他语言一样,是为了将别人写好的 .py 文件引入,并用于自己使用 例如我在一个.py 文件中写了很多用于计数学计算的方法,当别人想要调用我写好的这一套方法时 就需要先 from 我写的文件或其他人写好的文件(py…...

Composer安装与配置详解
目录 第一章:Composer简介 1.1 什么是Composer? 1.2 Composer与传统的依赖管理工具的区别 1.3 Composer的发展历程 1.4 本章小结 第二章:Composer安装 2.1 全局安装与项目内安装 2.1.1 全局安装 安装步骤 2.1.2 项目内安装 安装步骤 2.2 不同操作系统下的安装方…...

A5 STM32_HAL库函数 之 CAN通用驱动程序所有函数的介绍及使用
A5 STM32_HAL库函数 之 CAN通用驱动程序所有函数的介绍及使用 1 CAN通用驱动程序所有函数预览1.1 HAL_CAN_Init1.2 HAL_CAN_ConfigFilter1.3 HAL_CAN_DeInit1.4 HAL_CAN_MspInit1.5 HAL_CAN_MspDeInit1.6 HAL_CAN_Transmit1.7 HAL_CAN_Transmit_IT1.8 HAL_CAN_Receive1.9 HAL_C…...

python如何判断图片为黑白还是彩色
基本原理 灰度图分两种情况: 单通道的图片 RGB 三通道的图片,但是每个通道的值相等 对于单通道的图片只需要判断图片的通道值是否为1 对于RGB模式的图片,情况稍稍复杂些。理论上只需判断RGB三个通道的值是否相等,但是现实中灰度…...
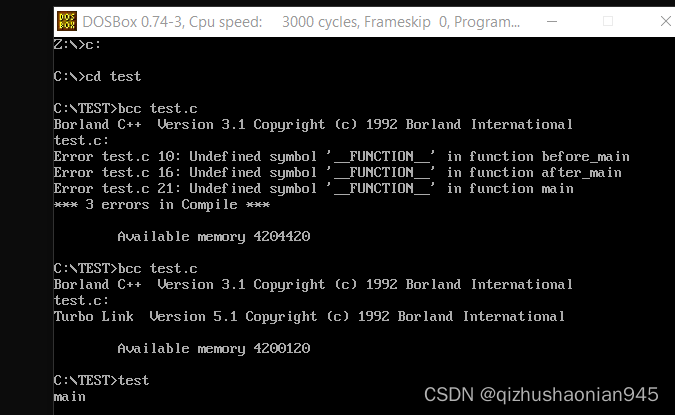
C语言进阶课程学习记录-main函数与命令行参数
C语言进阶课程学习记录-main函数与命令行参数 main函数验证以下4中定义是否正确实验-main的返回值cmd窗口 实验-main的输入参数cmd窗口 在main函数执其执行的函数实验-程序执行的第一个函数gcc编译器cmd窗口bcc编译器 小结 本文学习自狄泰软件学院 唐佐林老师的 C语言进阶课程&…...

Utilize webcam to capture photo with camera
1. Official Guide& my github Official course my github 2. Overcome Webcam js Error in Chrome: Could not access webcam link 直接把代码拷贝到本机的下述目录下 To ignore Chrome’s secure origin policy, follow these steps. Navigate to chrome://flags/#un…...
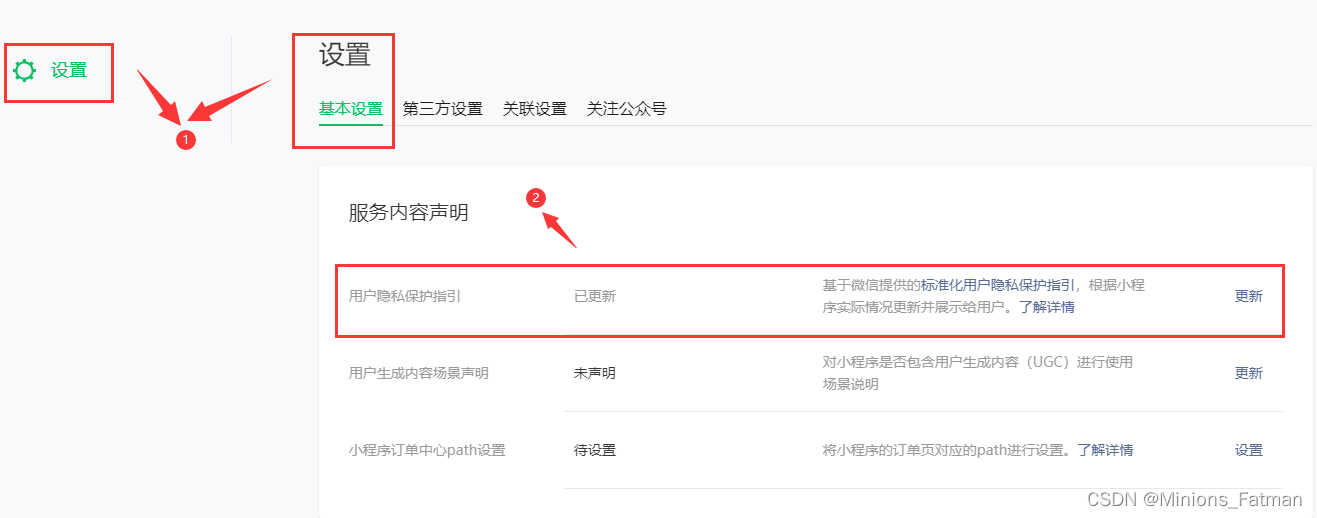
【uniapp】开发微信小程序 — 注意事项
底部导航栏 (tabBar) 图标的正确做法: 1、图片的标准尺寸为 81px * 81px,该尺寸在官方的文档中有明确的说明,可以参考微信小程序全局配置文档中对 iconPath 属性的说明。 2、为了保持良好的间距,图片的内容区域设置 60px* 比较好&…...
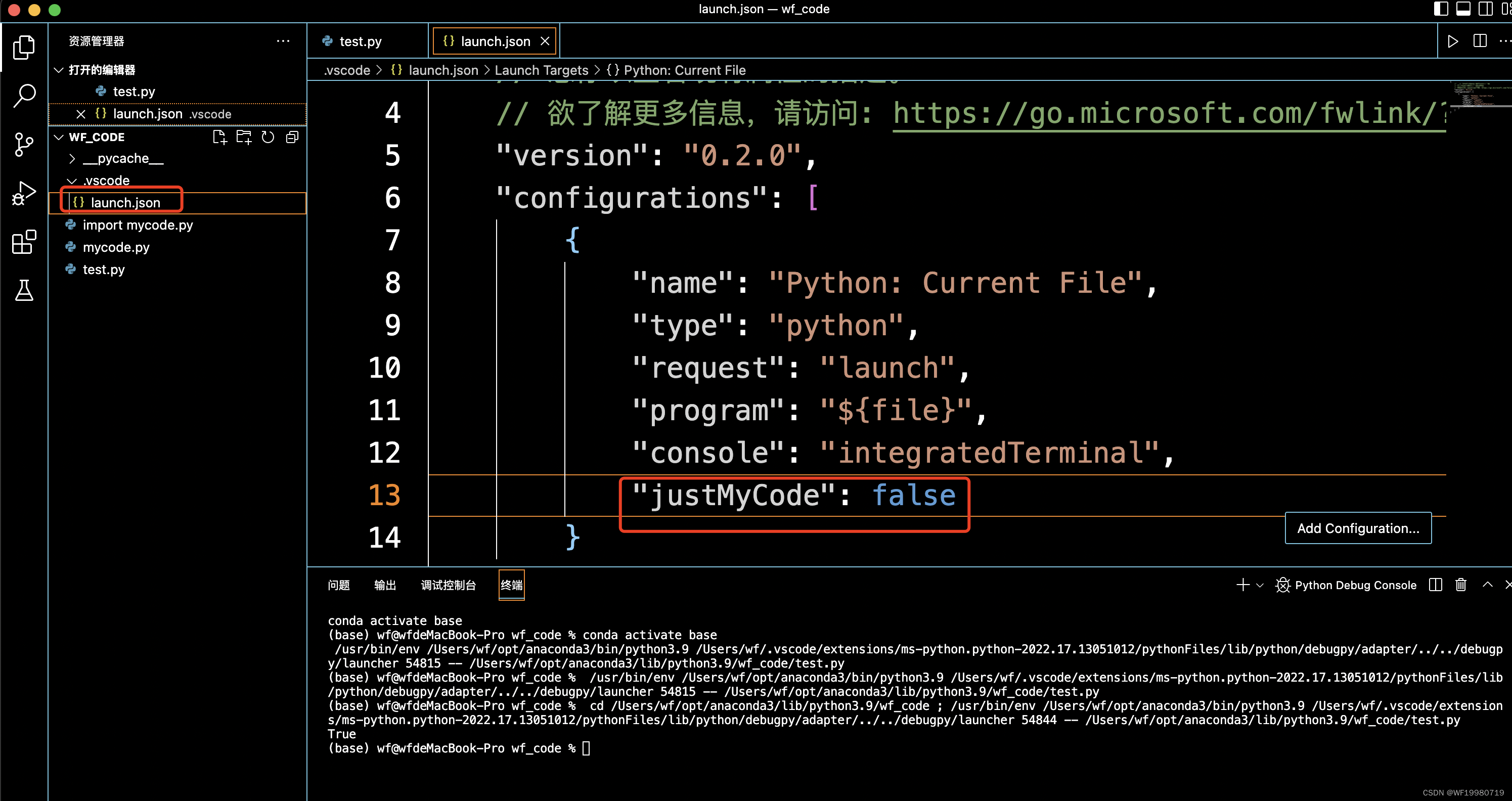
the python tutorial
Using the Python Interpreter Using Python as a Calculator To do floor division and get an integer result you can use the // operator Problem Solving with Algorithms and Data Structures using Python 首先将其拉到本地? 按照craft的方式走一遍&…...

AIoT人工智能物联网之AI 实战
1. jetson-inference 入门 jetson-inference是官方推出的体验套件,提供了三种最常见的AI应用于计算机视觉的类型,imagenet用于 图像辨识 ( Image Recognition )、detectNet用于对象辨识 ( Object Detection )、segNet用于语义分割 可以先使用windows下载 jetson-inference(因…...

Python 大麦抢票脚本
请注意,编写或使用抢票脚本可能违反相关网站的服务条款和法律法规。以下内容仅供学习和了解技术原理之用,不鼓励或支持任何违反规定的行为。 在Python中编写大麦网抢票脚本通常涉及以下几个步骤: ### 1. 分析网站结构 - 使用浏览器的开发者…...

前端开发攻略---用JavaScript打造炫酷数字变化动画效果:手写实现你的自定义动画函数!支持更改任意数字、动画速度
1、演示 2、介绍 这篇文章将向您展示如何使用JavaScript来创建一个自定义的动画函数,以实现数字变化效果。我们将深入了解前端动画的本质,并通过手写代码来实现这个炫酷的数字变化动画效果。您将学到如何利用JavaScript来操作DOM元素,控制动画…...

【学习】移动端兼容性测试有什么方法及重要性
随着移动互联网的快速发展,移动应用程序已经成为人们日常生活中不可或缺的一部分。然而,由于各种移动设备的硬件和软件差异,移动应用程序的兼容性问题也越来越突出。因此,移动端兼容性测试成为了一个重要的环节,它可以…...
记录linux从0部署java项目(宝塔)
目录 一、安装宝塔可视化界面 二、部署前端 三、部署后端 1、配置并连接Mysql数据库 2、配置并连接redis 3、安装jdk 这里先记录一个安装后遇到的问题 安装openJDK 四、检查 一、安装宝塔可视化界面 宝塔面板下载,免费全能的服务器运维软件 运行安装脚本 安…...

Python的时间和日期:探索datetime模块
🚀 个人主页:xmp65535 🚀 专栏:python技术专栏 目录 一、前言 二、datetime 模块简介 三、基本使用 1.日期和时间的创建 2.获取当前日期和时间 3.时间戳与日期时间之间的转换 4.时间运算 5.格式化日期和时间 6.解析字符串…...

代理与反向代理
Java项目的代理与反向代理 1. 代理 定位:为客户端服务通信方向:客户端->代理服务器->远程服务器好处:对客户端行为进行过滤和控制;隐藏客户端IP地址;审计流量;缓存资源加快访问速度; 2…...

长风破浪会有时,直挂云帆济沧海
仅以此篇记录生活琐事,因为自己在初中就天天写日记,到了大学自己写日记的次数逐渐少了下来。 最近心不在焉,不知道为啥,也许是因为压力吧。在我这个年龄阶段的压力也许不一样吧,过几天又要参加自考的考试,自…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
