【图论】Leetcode 200. 岛屿数量【中等】
岛屿数量
- 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
解题思路
- 1、使用深度优先搜索DFS来遍历二维网格,找到所有岛屿。(PS: 深度优先搜索(DFS)一般是使用递归来实现)
- 2、对于每个遍历到的陆地(‘1’),开始进行搜索,将其与相邻的陆地标记为已访问过,直到将整个岛屿搜索完成。
- 3、统计搜索过程中遇到的岛屿数量。
Java实现
public class NumberOfIslands {public int numIslands(char[][] grid) {if (grid == null || grid.length == 0 || grid[0].length == 0) {return 0;}int m = grid.length;int n = grid[0].length;int count = 0;
// {'1', '1', '0', '0', '0'},
// {'1', '1', '0', '0', '0'},
// {'0', '0', '1', '0', '0'},
// {'0', '0', '0', '1', '1'}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == '1') {// 当前位置为陆地,开始进行深度优先搜索// 直到grid[i][j]周边没有相连的陆地dfs(grid, i, j);// 每开始一次搜索,岛屿数量加一count++;}}}return count;}/*** 深度优先搜索函数* @param grid* @param i* @param j*/private void dfs(char[][] grid, int i, int j) {int m = grid.length;int n = grid[0].length;// 边界条件和递归终止条件if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {return;}grid[i][j] = '0'; //将当前单元格标记为已访问//继续搜索当前位置的上、下、左、右四个方向,探索相邻的单元格//直到没有相邻的岛屿(grid[i][j] == '0')dfs(grid, i + 1, j);dfs(grid, i - 1, j);dfs(grid, i, j + 1);dfs(grid, i, j - 1);}public static void main(String[] args) {NumberOfIslands islands = new NumberOfIslands();char[][] grid = {{'1', '1', '0', '0', '0'},{'1', '1', '0', '0', '0'},{'0', '0', '1', '0', '0'},{'0', '0', '0', '1', '1'}};System.out.println("Number of islands: " + islands.numIslands(grid));}
}时间空间复杂度
-
时间复杂度:O(m * n),其中 m 和 n 分别是二维网格的行数和列数,因为需要遍历整个二维网格。
-
空间复杂度:O(m * n),深度优先搜索的递归调用可能达到 O(m * n) 的深度,其中 m 和 n 分别是二维网格的行数和列数。
相关文章:

【图论】Leetcode 200. 岛屿数量【中等】
岛屿数量 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外,你可以…...

酒店大厅装水离子雾化壁炉前和装后对比
在酒店大厅装水离子雾化壁炉之前和之后,大厅的氛围和体验会有显著的对比: 装水离子雾化壁炉之前: 传统感:在壁炉安装之前,大厅可能会有传统的装饰或者简单的暖气设备,缺乏现代化的元素。这种传统感可能会…...
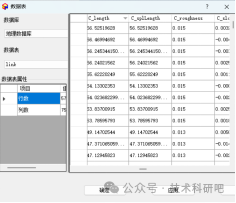
城市内涝与海绵城市规划设计中的水文水动力模拟
原文链接:城市内涝与海绵城市规划设计中的水文水动力模拟https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247601198&idx5&sn35b9e5e3961ea2f190f9742236a7217f&chksmfa820dc9cdf584df97633f64d19bdc3e5f7d1a5a85000c8f040e1953c51b9b39c87b5…...

C++项目实战与经验分享
在编程世界中,C++ 是一种功能强大且灵活的编程语言,广泛应用于系统级编程、游戏开发、嵌入式系统以及高性能计算等领域。本文将分享一个基于C++的图像处理系统项目实战经验,并深入探讨在开发过程中遇到的问题及解决方案。 一、项目概述 本次项目实战的目标是开发一个基于C…...

Day17_学点JavaEE_转发、重定向、Get、POST、乱码问题总结
1 转发 转发:一般查询了数据之后,转发到一个jsp页面进行展示 req.setAttribute("list", list); req.getRequestDispatcher("student_list.jsp").forward(req, resp);2 重定向 重定向:一般添加、删除、修改之后重定向到…...
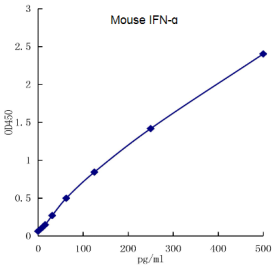
Mouse IFN-α ELISA kit (Quick Test)
干扰素α(IFN-α)是一类由免疫细胞分泌的内源性调节因子,也被称为白细胞干扰素,主要参与响应病毒感染的先天性免疫。 基于结构特征、受体、细胞来源和生物活性的不同,干扰素可被分为Ⅰ、Ⅱ、Ⅲ三种类型,其中…...
AMD Tensile 简介与示例
按照知其然,再知其所以然的认知次序进行 1,下载代码 git clone --recursive https://github.com/ROCm/Tensile.git 2,安装 Tensile cd Tensile mkdir build cd build ../Tensile/bin/Tensile ../Tensile/Configs/rocblas_dgemm_nn_asm_full…...
Rust语言
文章目录 Rust语言一,Rust语言是什么二,Rust语言能做什么?Rust语言的设计使其适用于许多不同的领域,包括但不限于以下几个方面:1. 传统命令行程序:2. Web 应用:3. 网络服务器:4. 嵌入…...

排序算法之冒泡排序
目录 一、简介二、代码实现三、应用场景 一、简介 算法平均时间复杂度最好时间复杂度最坏时间复杂度空间复杂度排序方式稳定性冒泡排序O(n^2 )O(n)O(n^2)O(1)In-place稳定 稳定:如果A原本在B前面,而AB,排序之后A仍然在B的前面; 不…...

js打印页面源码 ,打印选取的容器里的内容,打印指定内容
js打印页面源码 ,打印选取的容器里的内容,打印指定内容 效果 代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge&…...

算法练习第五十天|123.买卖股票的最佳时机III、188.买卖股票的最佳时机IV
123. 买卖股票的最佳时机 III 188. 买卖股票的最佳时机 IV 123.买卖股票的最佳时机III class Solution {public int maxProfit(int[] prices) {//dp[i][j] 第i天买卖股票获得的最大利润/**j0不操作j1第一次持有j2第一次不持有j3第二次持有j4第二次不持有dp[i][0] dp[i-1][0]d…...

细胞世界:4.细胞分化(划区域)与细胞衰老(设施磨损)
(1)细胞凋亡 1. 概念:细胞凋亡可以比作城市的规划者主动拆除某些建筑来更新城市或防止危险建筑对市民的潜在伤害。这是一个有序的过程,由城市(细胞内部)的特定规划(基因)所决定。 2. 特征:细…...
c语言:操作符
操作符 一.算术操作符: + - * % / 1.除了%操作符之外,其他的几个操作符可以作用与整数和浮点数,如:5%2.0//error. 2.对于操作符,如果两个操作数都为整数,执行整数除法而只要有浮点数执行的就是浮点数除法。 3.%操作符的两个操作数必须为整数。 二.移位操作符:<&…...

谷歌seo自然搜索排名怎么提升快?
要想在谷歌上排名快速上升,关键在于运用GPC爬虫池跟高低搭配的外链组合 首先你要做的,就是让谷歌的蜘蛛频繁来你的网站,网站需要被谷歌蜘蛛频繁抓取和索引,那这时候GPC爬虫池就能派上用场了,GPC爬虫池能够帮你大幅度提…...

Golang | Leetcode Golang题解之第13题罗马数字转整数
题目: 题解: var symbolValues map[byte]int{I: 1, V: 5, X: 10, L: 50, C: 100, D: 500, M: 1000}func romanToInt(s string) (ans int) {n : len(s)for i : range s {value : symbolValues[s[i]]if i < n-1 && value < symbolValues[s…...
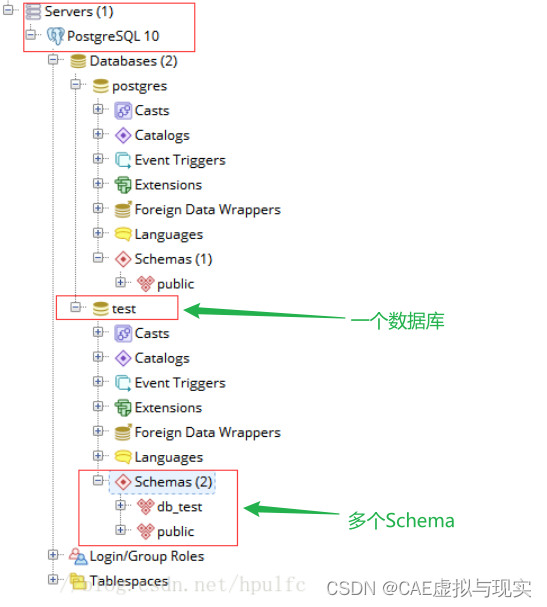
说说我理解的数据库中的Schema吧
一、SQL标准对schema如何定义? ISO/IEC 9075-1 SQL标准中将schema定义为描述符的持久命名集合(a persistent, named collection of descriptors)。 大部分的网上资料定义Schema如下: schema是用来组织和管理数据的一种方式。它…...

nginx 如何对用户屏蔽网站首页但是对蜘蛛开放
使用 Nginx 的 if 指令结合 $http_user_agent 变量来实现条件判断。不过,请注意,Nginx 官方文档通常建议避免在配置中过度使用 if 指令,因为它可能会导致不可预测的行为,尤其是在复杂的配置中。然而,对于简单的用例&am…...

【vue】ref 和 reactive 对比
ref:存储单个数据,如数值,字符串reactive:存储复杂数据,如对象,数组 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"vie…...

爬虫现在还有那么吃香嘛?
Python 作为一种广泛应用的编程语言,在 Web 开发、大数据开发、人工智能开发和嵌入式开发等领域都有着重要的应用。 Python 的易学性、清晰性和可移植性等特点使它得到很多技术人士的喜爱。对于数据科学和机器学习领域的程序员来说,Python 提供了强大的…...
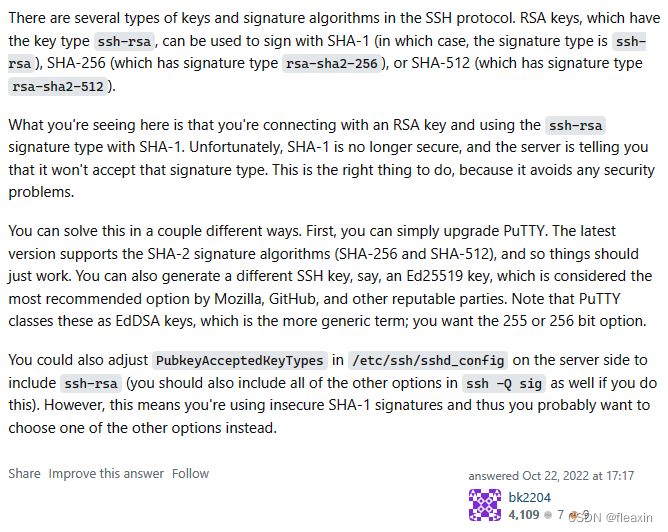
MobaXterm无法登陆oracle cloud的问题
问题 我在oracle cloud上创建实例的时候,只能使用密钥的方式登陆,当时下载了私钥文件。实例创建好以后,在mobaxterm上使用这个私钥文件无法登陆 排查 尝试使用mobaxterm的keygen,把私钥文件转成ppk格式,还是不行。…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
