当前位置： 首页 > news >正文

Golang | Leetcode Golang题解之第13题罗马数字转整数

news 2026/3/27 14:44:28

题目：

题解：

var symbolValues = map[byte]int{'I': 1, 'V': 5, 'X': 10, 'L': 50, 'C': 100, 'D': 500, 'M': 1000}func romanToInt(s string) (ans int) {n := len(s)for i := range s {value := symbolValues[s[i]]if i < n-1 && value < symbolValues[s[i+1]] {ans -= value} else {ans += value}}return
}

相关文章：

Golang | Leetcode Golang题解之第13题罗马数字转整数

题目&#xff1a; 题解&#xff1a; var symbolValues map[byte]int{I: 1, V: 5, X: 10, L: 50, C: 100, D: 500, M: 1000}func romanToInt(s string) (ans int) {n : len(s)for i : range s {value : symbolValues[s[i]]if i < n-1 && value < symbolValues[s…...

编程日记 2024/4/12 20:16:33

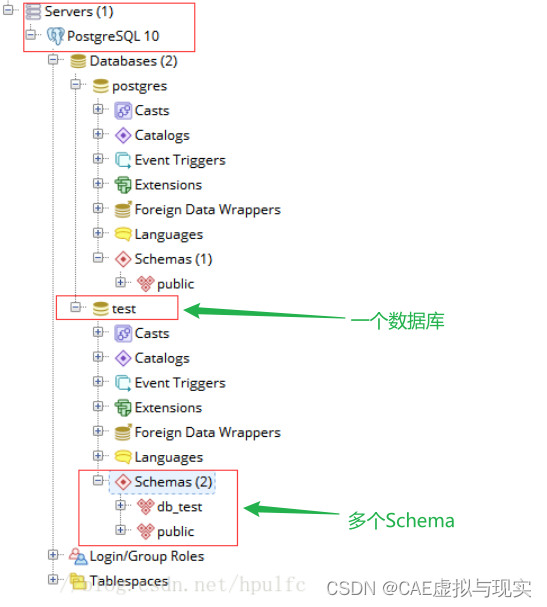
说说我理解的数据库中的Schema吧

一、SQL标准对schema如何定义&#xff1f; ISO/IEC 9075-1 SQL标准中将schema定义为描述符的持久命名集合&#xff08;a persistent, named collection of descriptors&#xff09;。 大部分的网上资料定义Schema如下&#xff1a; schema是用来组织和管理数据的一种方式。它…...

编程日记 2024/4/12 20:14:31

nginx 如何对用户屏蔽网站首页但是对蜘蛛开放

使用 Nginx 的 if 指令结合 $http_user_agent 变量来实现条件判断。不过&#xff0c;请注意&#xff0c;Nginx 官方文档通常建议避免在配置中过度使用 if 指令&#xff0c;因为它可能会导致不可预测的行为&#xff0c;尤其是在复杂的配置中。然而&#xff0c;对于简单的用例&am…...

编程日记 2024/4/12 20:13:30

【vue】ref 和 reactive 对比

ref&#xff1a;存储单个数据&#xff0c;如数值&#xff0c;字符串reactive&#xff1a;存储复杂数据&#xff0c;如对象&#xff0c;数组 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"vie…...

编程日记 2024/4/12 20:11:26

爬虫现在还有那么吃香嘛？

Python 作为一种广泛应用的编程语言&#xff0c;在 Web 开发、大数据开发、人工智能开发和嵌入式开发等领域都有着重要的应用。 Python 的易学性、清晰性和可移植性等特点使它得到很多技术人士的喜爱。对于数据科学和机器学习领域的程序员来说&#xff0c;Python 提供了强大的…...

编程日记 2024/4/12 20:10:23

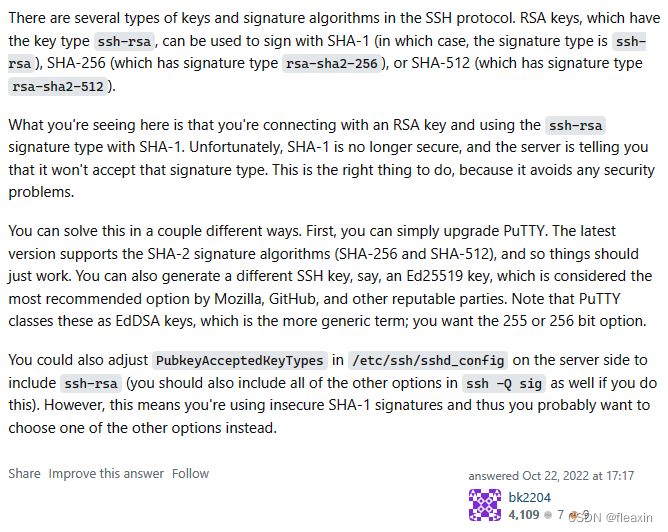
MobaXterm无法登陆oracle cloud的问题

问题 我在oracle cloud上创建实例的时候&#xff0c;只能使用密钥的方式登陆&#xff0c;当时下载了私钥文件。实例创建好以后&#xff0c;在mobaxterm上使用这个私钥文件无法登陆 排查 尝试使用mobaxterm的keygen&#xff0c;把私钥文件转成ppk格式&#xff0c;还是不行。…...

编程日记 2024/4/12 20:09:22

VLL: a lock manager redesign for main memory database systems阅读

为何要有VLL&#xff1f;VLL旨在解决什么问题&#xff1f; 在数据库系统中&#xff0c;锁是广泛使用的并发控制机制。然而对于内存数据库系统&#xff0c;锁管理器却成为了性能瓶颈所在。 一项研究说明内存数据库中有16%&#xff5e;25%的时间用于与锁管理器的交互 在传统的锁…...

编程日记 2024/4/12 20:08:21

REST API实战演练之JavaScript使用Rest API

咱们前面讲了一下如何创建REST API 假期别闲着&#xff1a;REST API实战演练之创建Rest API-CSDN博客 又讲了java客户端如何使用REST API 假期别闲着&#xff1a;REST API实战演练之客户端使用Rest API-CSDN博客 接下来咱们看看JavaScript怎么使用REST API。 一、新建一个…...

编程日记 2024/4/12 20:07:19

期货量化交易软件：MQL5 中的范畴论 (第 15 部分)函子与图论

概述 在上一篇文章中&#xff0c;我们目睹了前期文章中涵盖的概念&#xff08;如线性序&#xff09;如何视作范畴&#xff0c;以及为什么它们的“态射”在与其它范畴相关时即构成函子。在本文中&#xff0c;我们赫兹量化软件将阐述来自前期文章中的概括&#xff0c;即通过查看…...

编程日记 2024/4/12 20:05:17

2024妈妈杯数学建模B题思路-甲骨文智能识别中原始拓片单字自动分割与识别研究

# 1 赛题 B 题 甲骨文智能识别中原始拓片单字自动分割与识别研究 甲骨文是我国目前已知的最早成熟的文字系统&#xff0c;它是一种刻在龟甲或 兽骨上的古老文字。甲骨文具有极其重要的研究价值&#xff0c;不仅对中国文明的 起源具有重要意义&#xff0c;也对世界文明的研究有着…...

编程日记 2024/4/12 20:04:16

sql 之 索引

索引是对数据库表中一列或多列的值进行排序的一种结构&#xff0c;使用索引可快速访问数据库表中的特定信息。 1. 什么是索引 官方上面说索引是帮助MySQL高效获取数据的数据结构&#xff0c;通俗点来说&#xff0c;数据库索引就像是是一本书的目录&#xff0c;可以直接根据页码…...

编程日记 2024/4/12 20:02:14

创建基于Node的WebSocket服务

一：安装nodejs与npm apt-get install nodejs npm 但这种方法安装的版本可能偏低，影响后续的 npm install ws wscat。 按照 How to Install Node.js and npm on Ubuntu 18.04 | Linuxize里的步骤安装： 1、curl -sL https://deb.nodesource.com/setup_12.x | sudo -E bash …...

编程日记 2024/4/12 20:01:13

Flask快速搭建文件上传服务与接口

说明&#xff1a;仅供学习使用&#xff0c;请勿用于非法用途&#xff0c;若有侵权&#xff0c;请联系博主删除 作者&#xff1a;zhu6201976 一、需求背景 前端通过浏览器&#xff0c;访问后端服务器地址&#xff0c;将目标文件进行上传。 访问地址&#xff1a;http://127.0.0…...

编程日记 2024/4/12 19:56:08

AI算力报告：算力大时代，AI算力产业链全景梳理

今天分享的是AI算力专题系列深度研究报告&#xff1a;《算力大时代&#xff0c;AI算力产业链全景梳理》。 &#xff08;报告出品方&#xff1a;中信建投证券&#xff09; 报告共计&#xff1a;98页 核心观点 生成式 AI取得突破&#xff0c;我们对生成式 A 带来的算力需求做…...

编程日记 2024/4/12 19:53:06

点击上传文件

一、页面样式&#xff1a; &#xff08;1&#xff09;点击前&#xff1a; &#xff08;2&#xff09;点击后&#xff1a; 设计&#xff1a;①自定义elementPlus图标&#xff1b;②使用Tooltip实现鼠标悬浮按钮上出现文字提示&#xff1b;③上传与更换的切换样式&#xff1b;…...

编程日记 2024/4/12 19:52:04

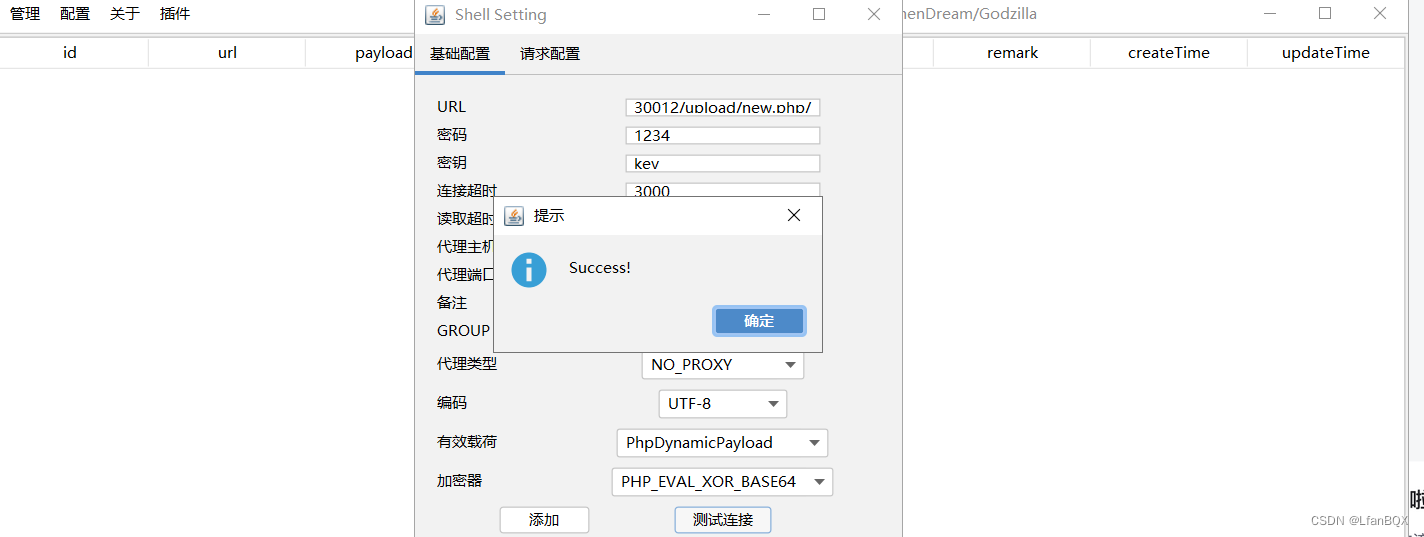
文件上传【2】--靶场通关

1.前端禁用js绕过 上传文件&#xff0c;进行抓包&#xff0c;没有抓到&#xff0c;说明这里的验证是前端js验证跳出的弹窗 禁用js后&#xff0c;php文件上传成功。 2.文件上传.htaccess 上传png木马后连接不上 代码中存在.htaccess&#xff0c;判断此时应该就是需要用到.htac…...

编程日记 2024/4/12 19:51:00

uniapp请求后端接口

新建文件夹utils const request (config) > {// 拼接完整的接口路径config.url http://mm.test.cn config.url;//这里拼接的是访问后端接口的地址&#xff0c;http://mm.test.cn/prod-api/testconsole.log(config.url)//判断是都携带参数if(!config.data){config.data …...

编程日记 2024/4/12 19:48:58

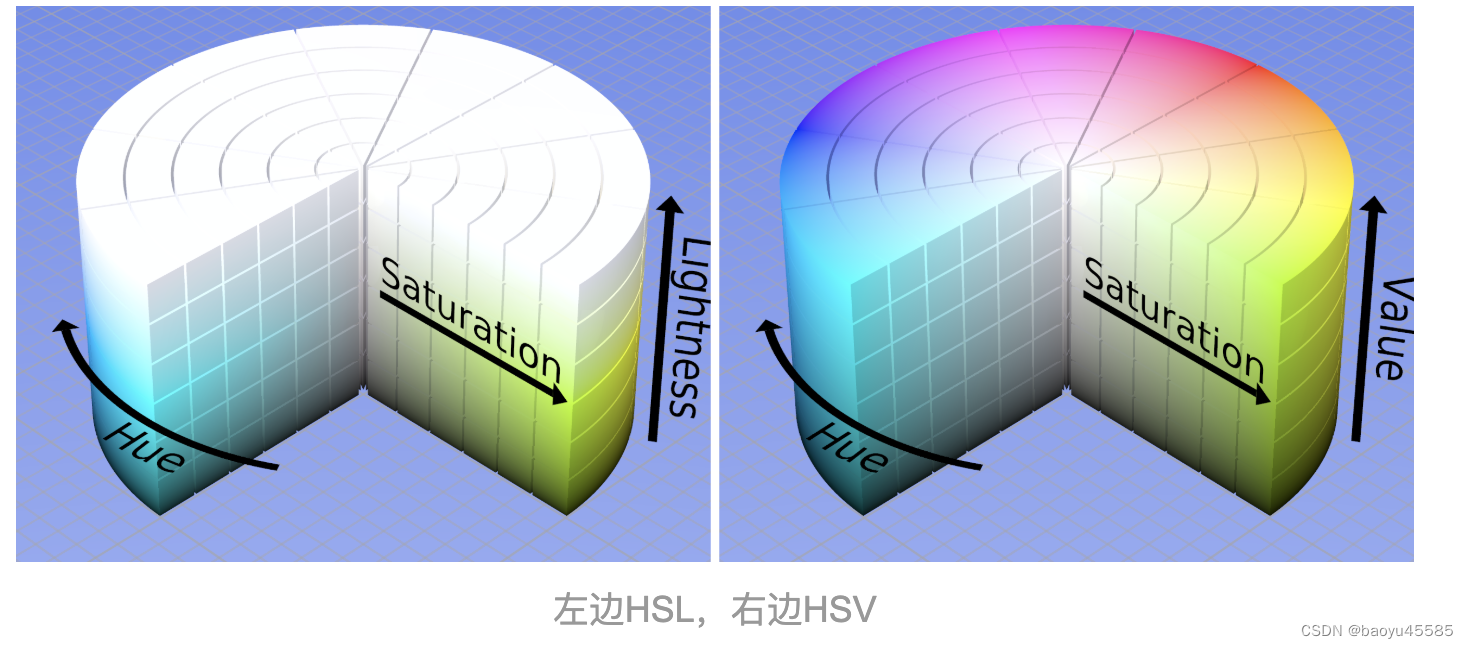
第十三章 OpenGL ES-RGB、HSV、HSL模型介绍

第十三章 OpenGL ES-RGB、HSV、HSL模型详细介绍 第一章 OpenGL ES 基础-屏幕、纹理、顶点坐标 第二章 OpenGL ES 基础-GLSL语法简单总结 第三章 OpenGL ES 基础-GLSL渲染纹理 第四章 OpenGL ES 基础-位移、缩放、旋转原理 第五章 OpenGL ES 基础-透视投影矩阵与正交投影矩阵…...

编程日记 2024/4/12 19:47:57

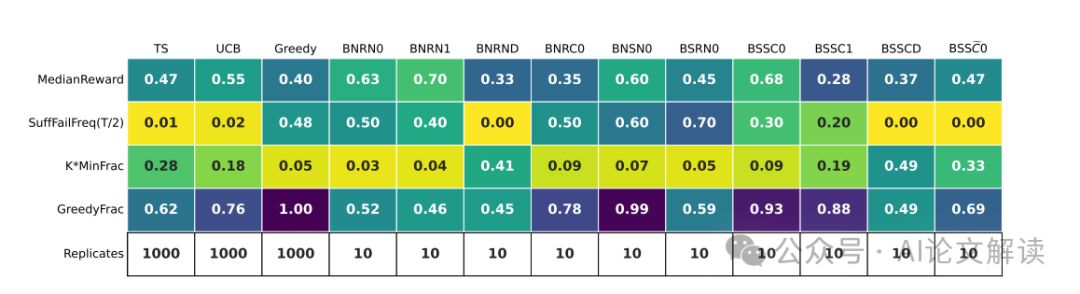
微软卡内基梅隆大学：无外部干预，GPT4等大语言模型难以自主探索

目录 引言&#xff1a;LLMs在强化学习中的探索能力探究 研究背景&#xff1a;LLMs的在情境中学习能力及其重要性 实验设计&#xff1a;多臂老虎机环境中的LLMs探索行为 实验结果概览&#xff1a;LLMs在探索任务中的普遍失败 成功案例分析&#xff1a;Gpt-4在特定配置下的探…...

编程日记 2024/4/12 19:46:56

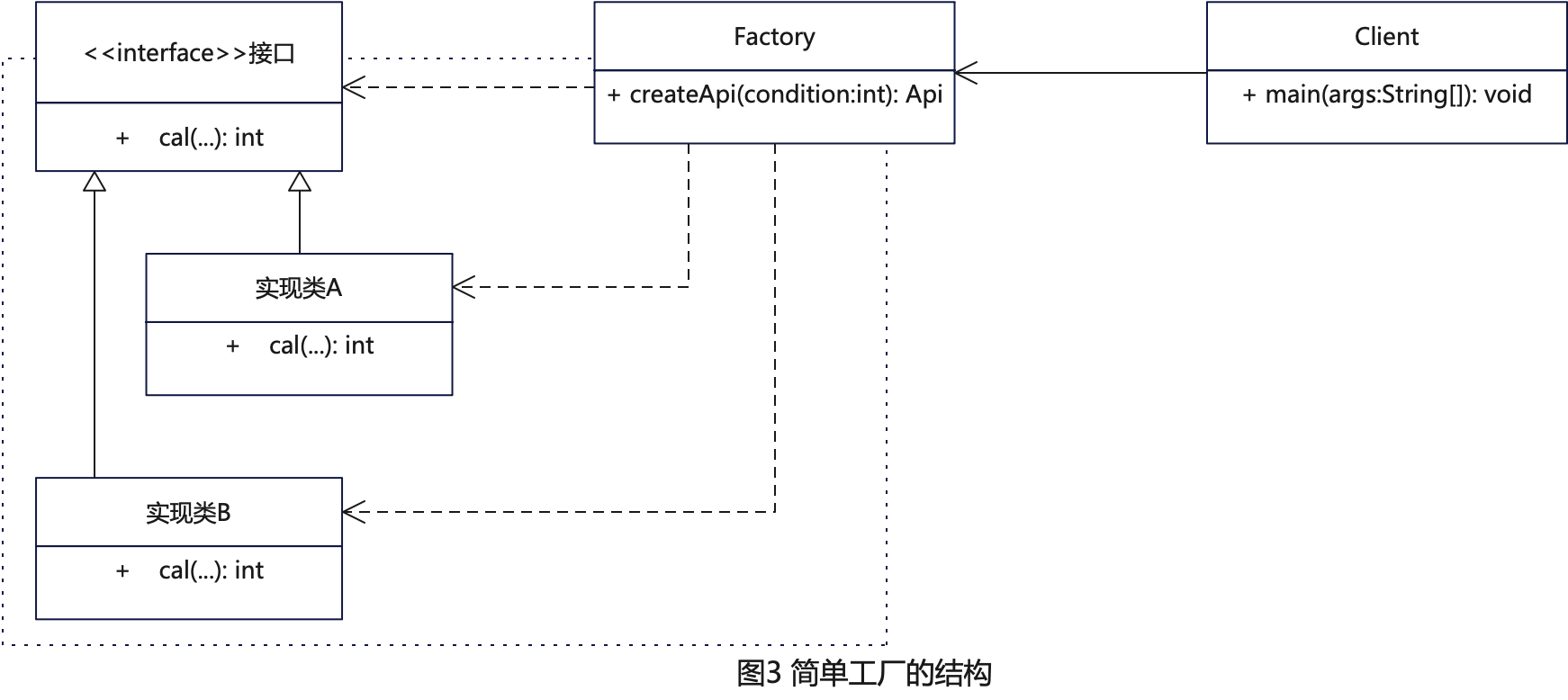
探索设计模式的魅力：简单工厂模式

个人主页: danci_ &#x1f525;系列专栏&#xff1a;《设计模式》《MYSQL应用》 &#x1f4aa;&#x1f3fb; 制定明确可量化的目标&#xff0c;坚持默默的做事。 &#x1f680; 转载自热榜文章&#xff1a;探索设计模式的魅力&#xff1a;简单工厂模式 简单工厂模式&#x…...

编程日记 2024/4/12 19:44:54

OpenClaw自动化测试：百川2-13B量化模型多场景准确率评估

OpenClaw自动化测试&#xff1a;百川2-13B量化模型多场景准确率评估 1. 测试背景与目标 去年冬天&#xff0c;我在为团队寻找一个能处理本地自动化任务的AI助手时&#xff0c;偶然发现了OpenClaw这个开源框架。当时最让我头疼的是&#xff0c;市面上的大模型要么太贵&#xf…...

编程新知 2026/3/27 14:24:25

当欧姆龙NX1P2遇上丰田PC10G：一次EIP实例ID通信的“踩坑”与“填坑”实录

当欧姆龙NX1P2遇上丰田PC10G&#xff1a;EIP实例ID通信的实战解析 在工业自动化领域&#xff0c;不同品牌设备间的通信集成往往充满挑战。最近一次非标设备联调项目中&#xff0c;我们遇到了欧姆龙NX1P2控制器与丰田PC10G设备通过EtherNet/IP&#xff08;EIP&#xff09;协议通…...

编程新知 2026/3/27 13:31:09

DeepSeek-OCR开源镜像多场景实践：跨境电商多语言产品说明书自动本地化预处理

DeepSeek-OCR开源镜像多场景实践&#xff1a;跨境电商多语言产品说明书自动本地化预处理 1. 项目背景与价值 跨境电商企业在全球化运营中面临着一个共同挑战&#xff1a;产品说明书的多语言本地化。传统方式需要人工翻译、重新排版设计&#xff0c;整个过程耗时耗力且成本高昂…...

编程新知 2026/3/27 12:52:53

5倍效率提升：GIMP批量图像处理插件BIMP全攻略

5倍效率提升&#xff1a;GIMP批量图像处理插件BIMP全攻略 【免费下载链接】gimp-plugin-bimp 项目地址: https://gitcode.com/gh_mirrors/gi/gimp-plugin-bimp 在数字内容创作领域&#xff0c;批量图像处理是提升效率的关键环节。GIMP作为免费开源的图像编辑软件&#…...

编程新知 2026/3/27 12:50:50

Obsidian插件本地化全攻略：从英文界面到中文体验的完整实施路径

Obsidian插件本地化全攻略&#xff1a;从英文界面到中文体验的完整实施路径 【免费下载链接】obsidian-i18n 项目地址: https://gitcode.com/gh_mirrors/ob/obsidian-i18n 在全球化协作与知识管理的场景中&#xff0c;Obsidian插件的英文界面常成为用户高效使用的障碍。…...

编程新知 2026/3/27 12:16:27

跨平台终端工具cmatrix：打造震撼的数字雨可视化效果

跨平台终端工具cmatrix&#xff1a;打造震撼的数字雨可视化效果 【免费下载链接】cmatrix Terminal based "The Matrix" like implementation 项目地址: https://gitcode.com/gh_mirrors/cm/cmatrix 你是否曾幻想过在自己的终端中重现《黑客帝国》里令人着迷的…...

编程新知 2026/3/27 11:27:59

OpenClaw更换stepfun/step-3.5-flash模型报错：Unknown model 解决（核心：漏加前缀）

OpenClaw更换stepfun/step-3.5-flash模型报错&#xff1a;Unknown model 解决&#xff08;核心&#xff1a;漏加前缀&#xff09; 摘要&#xff1a;本文聚焦OpenClaw更换stepfun/step-3.5-flash:free模型时&#xff0c;高频报错「Unknown model」的核心解决方法——忘记给主模…...

编程新知 2026/3/27 10:57:51

DeepSeek-OCR-2开发者案例：集成至RAG系统实现图文混合检索增强

DeepSeek-OCR-2开发者案例&#xff1a;集成至RAG系统实现图文混合检索增强 1. 项目背景与需求 最近在做一个智能文档问答系统&#xff0c;客户的需求很明确&#xff1a;他们有很多PDF文档&#xff0c;里面既有文字又有图片&#xff0c;用户提问时&#xff0c;系统要能同时理解…...

编程新知 2026/3/27 9:53:19

终极指南：如何让2007年旧Mac运行最新macOS系统

终极指南&#xff1a;如何让2007年旧Mac运行最新macOS系统 【免费下载链接】OpenCore-Legacy-Patcher 体验与之前一样的macOS 项目地址: https://gitcode.com/GitHub_Trending/op/OpenCore-Legacy-Patcher 还在为那台陪伴多年的老Mac无法升级最新系统而烦恼吗&#xff1…...

编程新知 2026/3/27 9:35:04

nli-distilroberta-base企业应用：HR简历筛选中‘要求’与‘经历’逻辑匹配系统

nli-distilroberta-base企业应用&#xff1a;HR简历筛选中要求与经历逻辑匹配系统 1. 项目背景与价值 在人力资源招聘流程中&#xff0c;简历筛选是最耗时的工作环节之一。传统的人工筛选方式面临两大核心痛点&#xff1a; 效率低下&#xff1a;HR需要逐份阅读简历&#xff…...

编程新知 2026/3/27 9:16:51