期货量化交易软件:MQL5 中的范畴论 (第 15 部分)函子与图论
概述
在上一篇文章中,我们目睹了前期文章中涵盖的概念(如线性序)如何视作范畴,以及为什么它们的“态射”在与其它范畴相关时即构成函子。在本文中,我们赫兹量化软件将阐述来自前期文章中的概括,即通过查看图论如何具有与上一篇文章中查看的线性序类似的用途。为了使用图论,我们赫兹量化将 MQL5 日历数据重构为图形,由此作为一个范畴。这将是一个关键焦点。本文的目的仍然会像我们之前的一篇,寻求明示在两个范畴之间函子的波动性预测潜力。不过,在这种情况下,我们的域范畴是一个图形,而协域将在预排序时间序列中显示标准普尔 500 指数波动率值(并非 VIX)。
MQL5 日历灌注数据重构为图形
当我们把范畴论与数据库制程联系起来时,MQL5 财经日历已被涵盖,故此在此重新涉及它与交易者的相关性并不适宜。为了将其表示为图形,即一连串的边线和节点,首先需要预先选择我们将包含在范畴中的新闻项目的子集。从财经日历网站上可以明显看出,有很多项目可供选择,不过,如果我们决定基于一个松散的假设只选择四个项目,并将它们连接起来,如下图所示:

添加图片注释,不超过 140 字(可选)
那么我们的假设会颇具争议,零售销售数字是制造业采购经理人指数(PMI)数据的函数,其派生自 CPI,而 CPI 又是由国债竞售业绩的结果而来,而国债竞售业绩也基于零售销售数字。因此,这是一个简单的循环,其准确性不是本文的主题,而更多意味着从财经日历数据勾勒可能的图形构图。
图论通过创建两个直截了当的表格,一个是顶点的配对表,另一个用作顶点的索引,来简化复杂的互连系统。图形可以被视为一个范畴,因为顶点可以被视为对象(域),这意味着边线当作态射。作为旁注,这与上一篇文章中看到的线性序有何不同,顾名思义,是线性。图论倾向于容纳更复杂的连接,其中对象/域可以连接到多个对象。
故此,我们不会像上一篇文章中关于线性序那样,将该范畴中的单个对象与标普波动率范畴中的对象配对,而是将顶点对的行数与标普范畴配对。这意味着它不能同构,由于鉴于标普是基于时间的,故多行被捆绑,并与标普中的单个对象(数据点)配对。这也意味着我们的域对象将构成四个元素(循环中四个项目的各自最后数值)。
范畴论和函子回顾
正如本文中已经提到的,范畴论已有许多应用,但大多数公开参考文献在代数拓扑方面倾向于零,这可能是因为该主题的原始作者,这就是为什么将 MQL5 应用于交易看似很新颖的原因。事实上,大多数熟悉 MQL5 的交易者倾向于使用神经网络来开发他们的前沿系统,或许是因为与范相比,它们经历的研究更久,这不应该阻止探索范畴,因为底线是大多数交易者都在寻求前沿,如果一个系统或方法太常见,那么能找到一个的几率就会降低。
函子,正如我们在上一篇文章中曾提过的,实际上是范畴之间的态射。这些“态射”不仅将两个范畴中的对象连接起来,而且还将范畴之间的同态连接起来。
在上一篇文章中,我们测试了两个场景,一个是使用两个范畴之间的对象连接,另一个是考虑相同范畴之间的态射连接。函子是两者的对数,出于我们的意图,尽管我们一次取一个来探索两者之间的差异,并为每个提供策略测试报告,这些突显出预测纳斯达克波动率的相对重要性。鉴于 2020年 1 月 1 日至 2020年 3 月 15 日的测试窗口较短,无法得出哪种映射更佳的结论,但结果当中的差异表明具有高度敏感性,因此需要强调一个盖过其它。
创建标准普尔 500 指数波动率范畴
SP500 波动率数据的收集和处理很简单,类似于我们在上一篇文章中衡量纳斯达克波动率的方式。VIX 是我们将在这里研究的单独指标,读者注意这一点很重要。故此,当前的波动率读数将在以下清单之后在每根新柱线上重新计算:
double _float_value=0.0; //where R is an instance of MqlRates... _float_value=(R.high-R.low)/Point();
如前所述,标普将形成我们的协域,对象捕获的波动率值作为一个对象的集合,以及它们之间的态射捕获波动率读数之间的相对变化。此范畴的初始化可以按如下方式处理:
正如我们在上一篇文章中所见,如果我们能将一个带有滞后的域映射到这个协域,我们就具备对标普 500 指数的波动性进行一些预测的能力。与上一篇文章一样,我们将在相同的信号和资金管理设置上分别测试对象和态射函子,从而衡量灵敏度。
从财经日历到标普 500 指数的函子
我们将使用以下清单构建财经日历数据的范畴:
该域中的每个对象都有两个顶点,它们是成对的日历值,其中至少有一个顶点位于协域中波动率值的时间范围内。由于这些财经数据大约每隔一个月发布一次,我们将在月度时间帧内进行测试。与上一篇文章一样,我们的函子映射将含有对象中每个数据点的系数。此处的区别在于,我们面临着多个对象映射到协域中同一波动性的可能性。理想情况下,我们需要分别从每个对象获取系数(对于线性映射),并在预测中使用它们。这意味着它们捆绑后必然会在态射映射提供的预测之上造成相互冲突的预测。这就是为什么出于本文目的,我们可以权衡从日历数据到标普范畴的每个函子映射,并将所有值的点积总和映射到波动率值。
相关文章:

期货量化交易软件:MQL5 中的范畴论 (第 15 部分)函子与图论
概述 在上一篇文章中,我们目睹了前期文章中涵盖的概念(如线性序)如何视作范畴,以及为什么它们的“态射”在与其它范畴相关时即构成函子。在本文中,我们赫兹量化软件将阐述来自前期文章中的概括,即通过查看…...

2024妈妈杯数学建模B题思路-甲骨文智能识别中原始拓片单字自动分割与识别研究
# 1 赛题 B 题 甲骨文智能识别中原始拓片单字自动分割与识别研究 甲骨文是我国目前已知的最早成熟的文字系统,它是一种刻在龟甲或 兽骨上的古老文字。甲骨文具有极其重要的研究价值,不仅对中国文明的 起源具有重要意义,也对世界文明的研究有着…...

sql 之 索引
索引是对数据库表中一列或多列的值进行排序的一种结构,使用索引可快速访问数据库表中的特定信息。 1. 什么是索引 官方上面说索引是帮助MySQL高效获取数据的数据结构,通俗点来说,数据库索引就像是是一本书的目录,可以直接根据页码…...

创建基于Node的WebSocket服务
一:安装nodejs与npm apt-get install nodejs npm 但这种方法安装的版本可能偏低,影响后续的 npm install ws wscat。 按照 How to Install Node.js and npm on Ubuntu 18.04 | Linuxize里的步骤安装: 1、curl -sL https://deb.nodesource.com/setup_12.x | sudo -E bash …...

Flask快速搭建文件上传服务与接口
说明:仅供学习使用,请勿用于非法用途,若有侵权,请联系博主删除 作者:zhu6201976 一、需求背景 前端通过浏览器,访问后端服务器地址,将目标文件进行上传。 访问地址:http://127.0.0…...

AI算力报告:算力大时代,AI算力产业链全景梳理
今天分享的是AI算力专题系列深度研究报告:《算力大时代,AI算力产业链全景梳理》。 (报告出品方:中信建投证券) 报告共计:98页 核心观点 生成式 AI取得突破,我们对生成式 A 带来的算力需求做…...
点击上传文件
一、页面样式: (1)点击前: (2)点击后: 设计:①自定义elementPlus图标;②使用Tooltip实现鼠标悬浮按钮上出现文字提示;③上传与更换的切换样式;…...
文件上传【2】--靶场通关
1.前端禁用js绕过 上传文件,进行抓包,没有抓到,说明这里的验证是前端js验证跳出的弹窗 禁用js后,php文件上传成功。 2.文件上传.htaccess 上传png木马后连接不上 代码中存在.htaccess,判断此时应该就是需要用到.htac…...

uniapp请求后端接口
新建文件夹utils const request (config) > {// 拼接完整的接口路径config.url http://mm.test.cn config.url;//这里拼接的是访问后端接口的地址,http://mm.test.cn/prod-api/testconsole.log(config.url)//判断是都携带参数if(!config.data){config.data …...
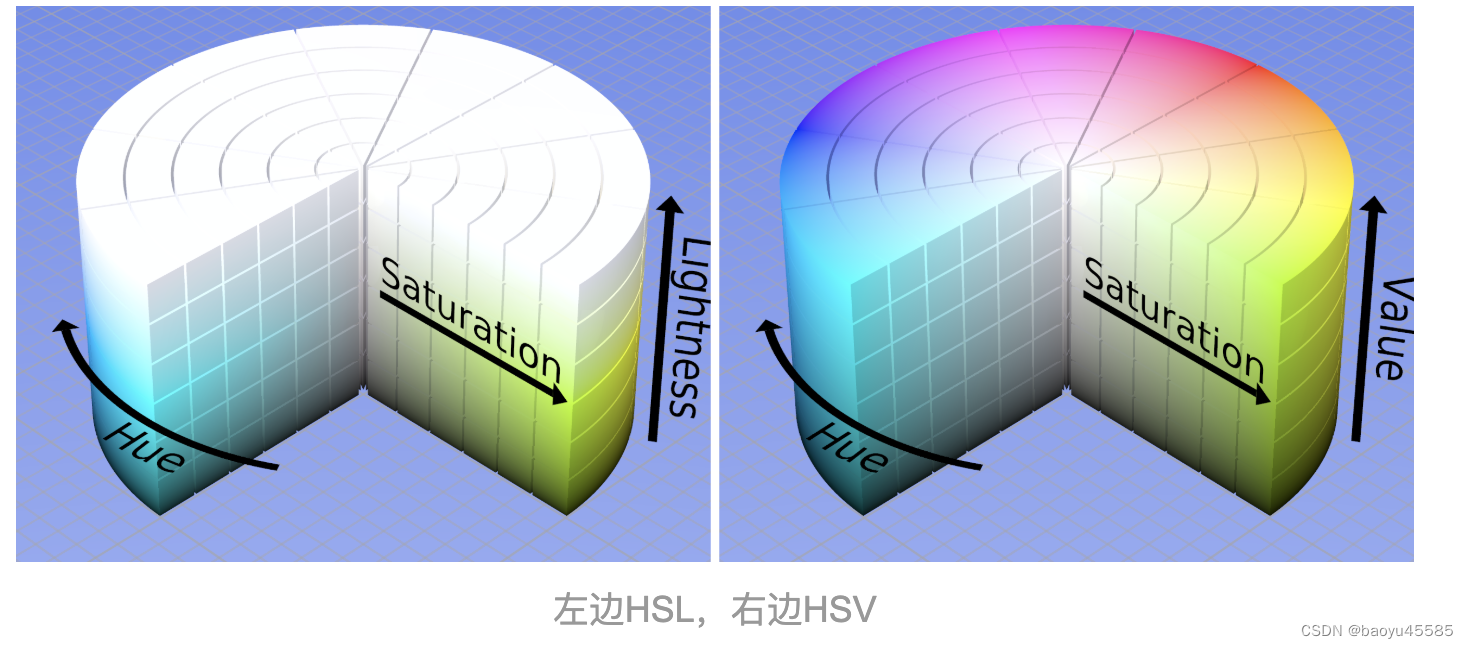
第十三章 OpenGL ES-RGB、HSV、HSL模型介绍
第十三章 OpenGL ES-RGB、HSV、HSL模型详细介绍 第一章 OpenGL ES 基础-屏幕、纹理、顶点坐标 第二章 OpenGL ES 基础-GLSL语法简单总结 第三章 OpenGL ES 基础-GLSL渲染纹理 第四章 OpenGL ES 基础-位移、缩放、旋转原理 第五章 OpenGL ES 基础-透视投影矩阵与正交投影矩阵…...
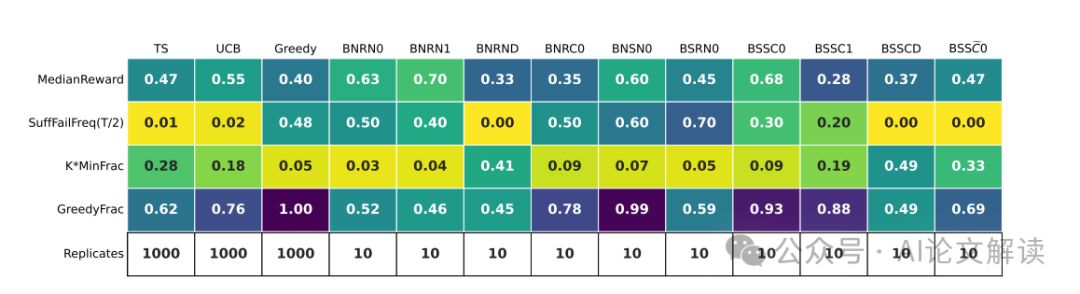
微软卡内基梅隆大学:无外部干预,GPT4等大语言模型难以自主探索
目录 引言:LLMs在强化学习中的探索能力探究 研究背景:LLMs的在情境中学习能力及其重要性 实验设计:多臂老虎机环境中的LLMs探索行为 实验结果概览:LLMs在探索任务中的普遍失败 成功案例分析:Gpt-4在特定配置下的探…...
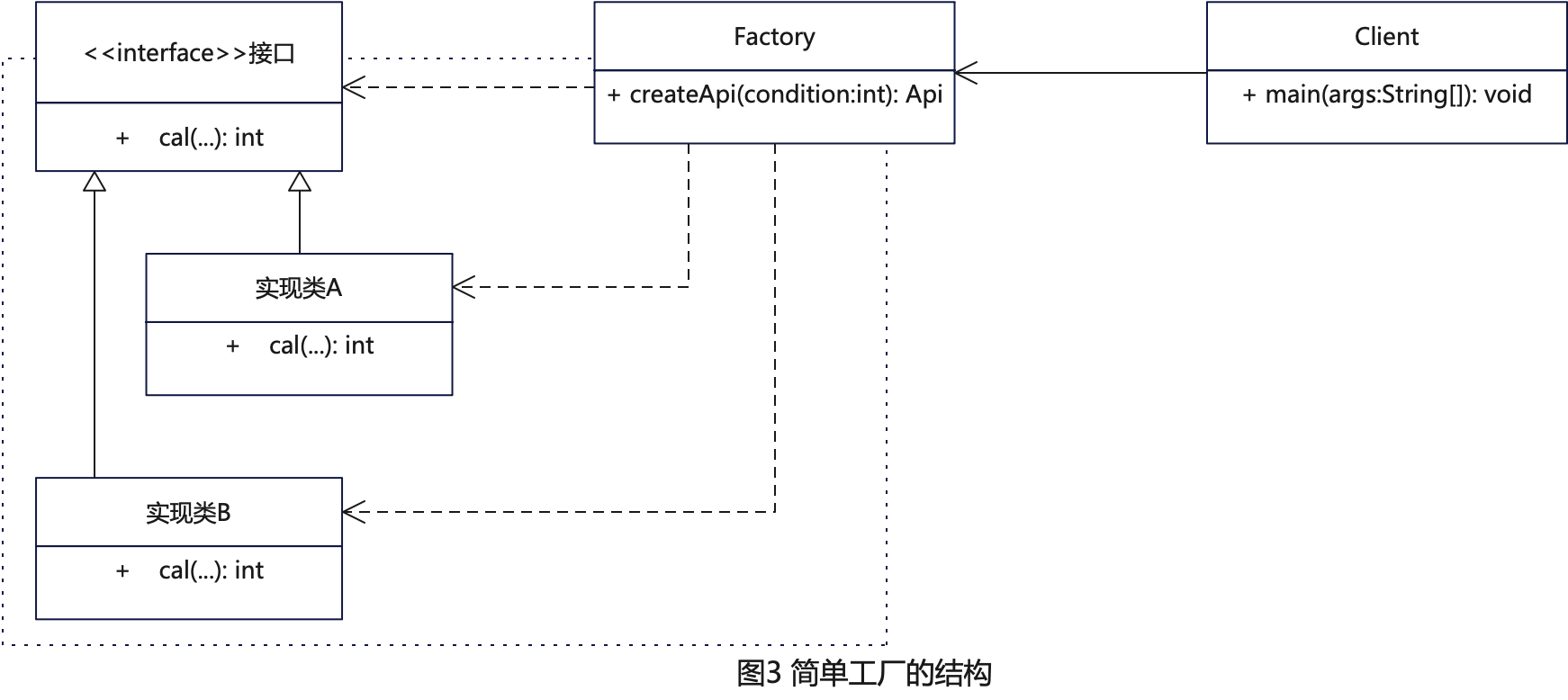
探索设计模式的魅力:简单工厂模式
个人主页: danci_ 🔥系列专栏:《设计模式》《MYSQL应用》 💪🏻 制定明确可量化的目标,坚持默默的做事。 🚀 转载自热榜文章:探索设计模式的魅力:简单工厂模式 简单工厂模式&#x…...

【数据结构】-----双链表(小白必看!!!)
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...
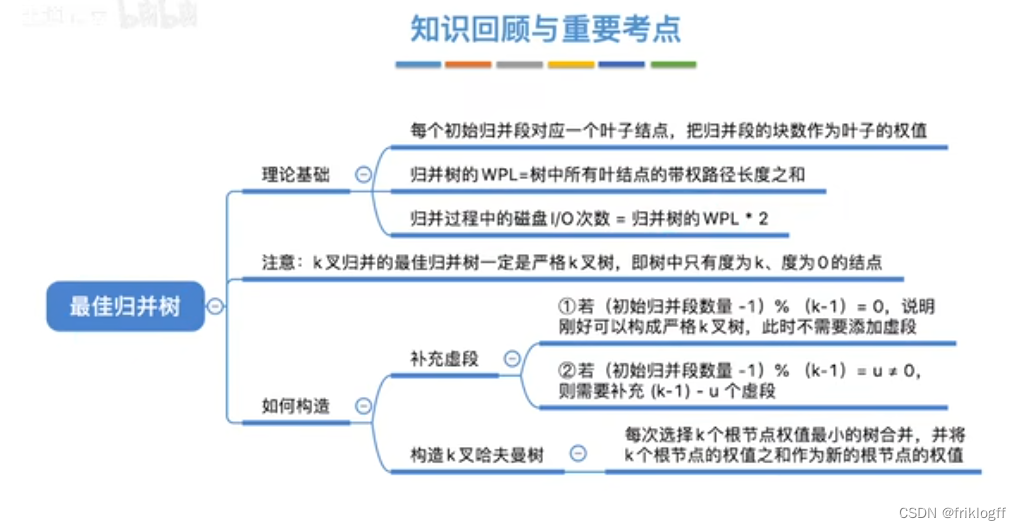
【数据结构】考研真题攻克与重点知识点剖析 - 第 8 篇:排序
前言 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图与王道考研课程,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术…...

数字乡村可视化大数据-DIY拖拽式设计
DIY拖拽式大数据自由设计万村乐可视化大数据V1.0 随着万村乐数字乡村系统的广泛使用,我们也接收到了客户的真实反馈,最终在公司的决定下,我们推出了全新的可视化大数据平台V1.0版本,全新的可视化平台是一个通过拖拽配置生成可视化…...

数据集学习
1,CIFAR-10数据集 CIFAR-10数据集由10个类的60000个32x32彩色图像组成,每个类有6000个图像。有50000个训练图像和10000个测试图像。 数据集分为五个训练批次和一个测试批次,每个批次有10000个图像。测试批次包含来自每个类别的恰好1000个随机…...
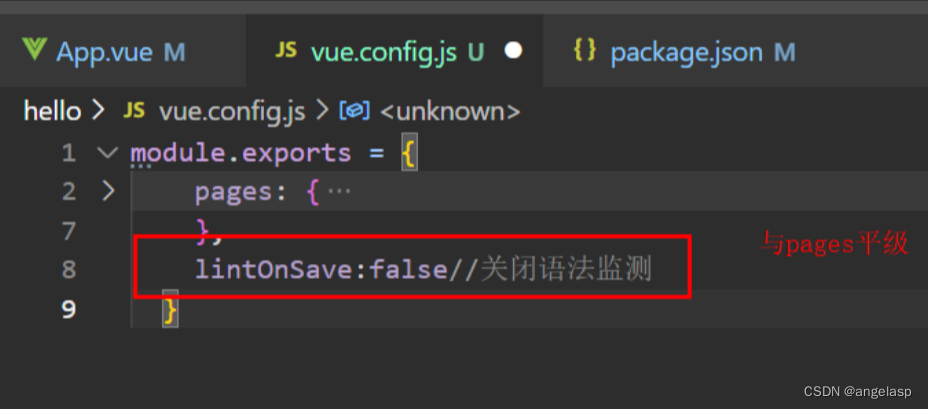
【解决】npm run dev Syntax Error: TypeError: eslint.CLIEngine is not a constructor
问题: 由于代码语法不符合eslint而照成此错误,可以参照eslint规则修改语法,或者将eslint停掉 以下为停掉eslint的方法。 You may use special comments to disable some warnings. Use // eslint-disable-next-line to ignore the ne…...

Android 如何通过屏幕大小来适配不同大小的图片
可以使用Android中的dp(密度无关像素)单位来设置不同屏幕密度下的图片大小。dp是Android中的一种尺寸单位,它与屏幕密度无关,只与字体大小有关。在开发过程中,可以使用dp来设置布局和控件的大小,以便在不同的屏幕密度下保持一致的…...

【面试题】细说mysql中的各种锁
前言 作为一名IT从业人员,无论你是开发,测试还是运维,在面试的过程中,我们经常会被数据库,数据库中最经常被问到就是MySql。当面试官问MySql的时候经常会问道一个问题,”MySQL中有哪些锁?“当我…...
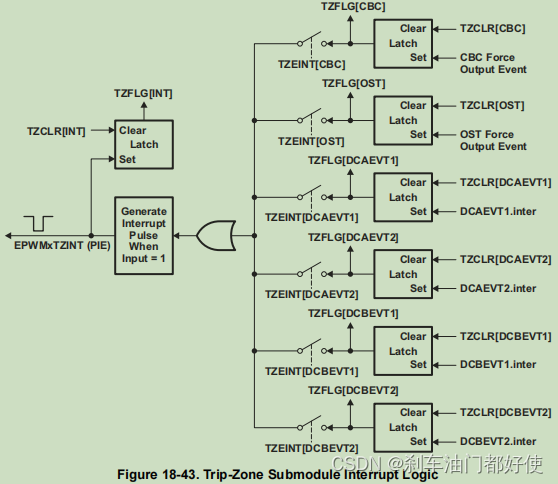
TMS320F280049 EPWM模块--TZ子模块(6)
下图是TZ子模块在epwm中的位置,可以看到TZ子模块接收内外部多种信号,经过处理后生成最终epwm波形,然后通过gpio向外发出。 TZ的动作有4个:拉高/拉低/高阻/不变。 TZ的内部框图见下图,可以看出: 1…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
