数学建模-最优包衣厚度终点判别法(主成分分析)
💞💞 前言
hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:viperrrrrrr的博客
💥 欢迎学习数学建模算法、大数据、前端等知识,让我们一起向目标进发!
基于近红外光谱的肠溶片最优包衣厚度终点判别法
包衣是将片剂的外表面均匀地包裹上一层衣膜的过程,旨在控制药物在胃肠道中的释放部位和速度,遮盖苦味或不良气味,防潮、避光,改善外观等。然而,包衣膜太薄或太厚都不利于药效,并且包衣终点的判断方法目前存在一定的难度。近红外光谱技术(NIRS)是一种高效、无需试剂、无污染的分析方法,通过近红外光谱仪、化学计量学软件和应用模型,能快速、简便地实现多组分检测。为实现包衣终点的准确判断,对数据进行分析并完成以下问题:
问题一:对药品在不同包衣时间段包衣片剂的近红外光谱进行特征峰提取,选择具有有效信息的波长片段,即波长选择。
问题二:分析药品包衣厚度分类规律,建立合适的模型对药品包衣不同厚度进行划分,给出方法及结果,并进行灵敏度分析。
问题三:对于不同的包衣厚度,通过建立模型分析包衣之间的关联性,判别出最优的包衣厚度。
我们本次主要解决问题一
问题一
包衣是将片剂均匀地包裹衣膜,用于控制药物释放、遮盖苦味等。然而,包衣膜太薄或太厚都不利于药效,并且包衣终点的判断方法目前存在一定的难度。而近红外光谱技术是一种无污染、快速、多组分检测的分析方法,它适用于包衣终点的确定。本文基于一批现有的红外光谱相关数据,建立主成分分析、聚类分析、Bayes判别等模型和梯度下降算法,实现了片剂包衣最佳终点的判断。建立了主成分分析模型进行特征峰选取,利用主成分分析中广泛使用的降维技术,通过线性变换将高维数据集转化为低维数据集,同时保留数据集中的主要信息。由于不同的特征会有不同的量纲,这可能会影响到模型的性能,因此在应用PCA之前,通常需要对数据进行数据预处理。列出协方差矩阵反映数据集中各特征之间相关性的矩阵。通过求解协方差矩阵的特征向量和特征值,可以得到数据集的主成分。这些主成分是原始特征空间中的线性变换,它们是新的、相互独立的、能够捕捉到数据变动的最大方差的向量。
首先,通过滑动平均滤波法对附件数据进行平滑处理,即滤波。基于附件数据,由图(1)可见原始波长噪音数据较多,会影响最终数据结果[1]。使用5倍滑动滤波进行降噪处理后,由图(2)可见,成功过滤了部分噪声数据,使光谱变得更加平滑。
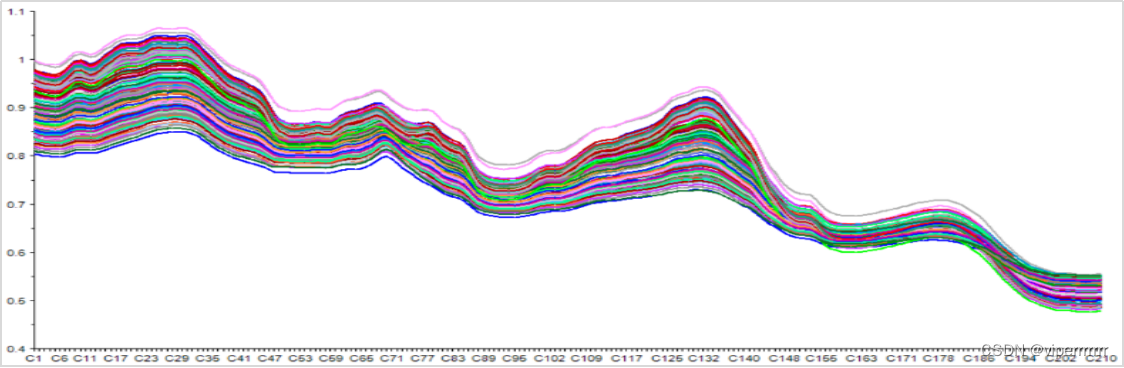
图1 原始数据图
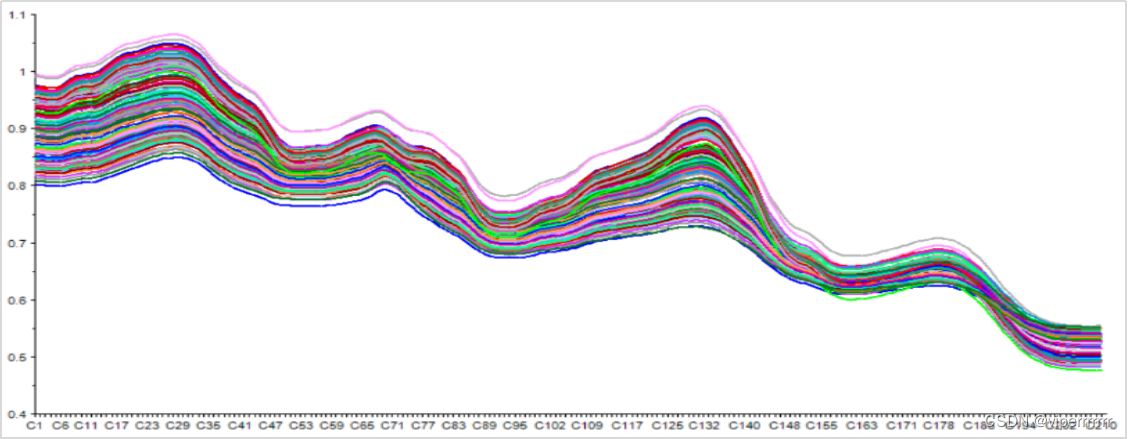
图2 5倍滑动滤波处理后数据图
5.1.2主成分分析模型
根据问题一的分析,我们建立了主成分分析模型进行了对不同包衣时间段包衣片剂的近红外光谱的特征峰选取。首先,将波长定义为X轴,在不同包衣时间下的片剂包衣、素片为Y 轴,在此基础上进行主成分分析,在进行特征根选取时,发现有两种情况可以选择,第一种情况是选取特征根大于1的成分,可以选取出2个主成分,第二种情况是按照公式(1)算取方差贡献率以选取特征根,可以选取出3个主成分。再算取累计方差贡献率以验证特征峰选取的合理性[2]。
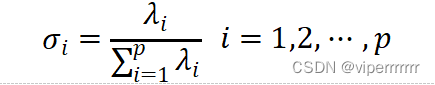 | (1) |
通过minitab(见附录)从中提取的2个主成分的特征值,对第一种情况进行分析,见图3,可知其得分向量(具体见附录)和特征根为:

,方差累计贡献率。说明选取的这两个主成分可以解释99.785%的原数据,具有较强的代表性。再对第二种情况进行分析,可以得到特征根和方差贡献率,方差累计贡献率
。
说明选取的这三个主成分可以解释99.897%的原数据,具有更强的代表性。但是对比第一种情况,代表性并提升幅度过小,综合考虑后,最终在问题一中选取第一种情况,即两个主成分为最终解。
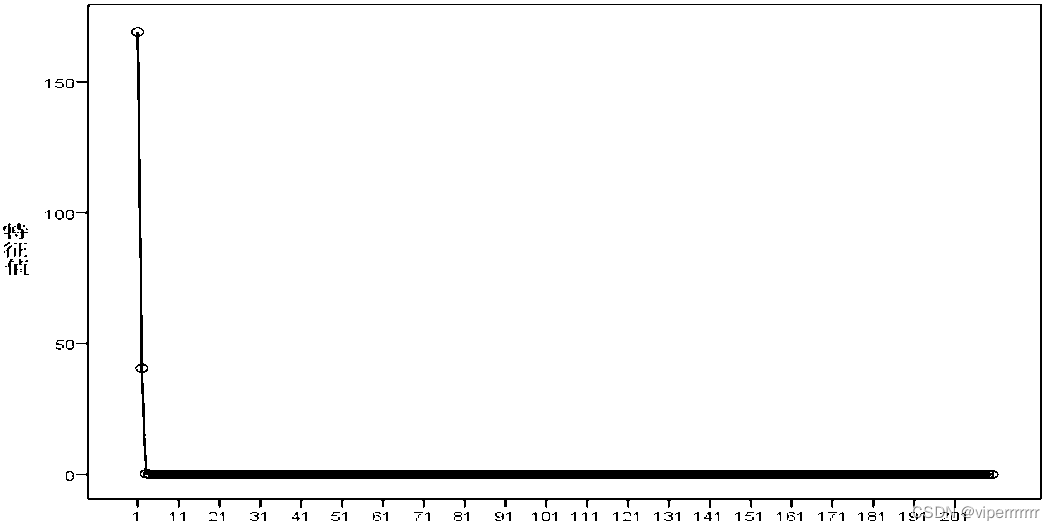
图3 主成分分析碎石图
相关文章:

数学建模-最优包衣厚度终点判别法(主成分分析)
💞💞 前言 hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页ÿ…...

Mysql内存表及使用场景(12/16)
内存表(Memory引擎) InnoDB引擎使用B树作为主键索引,数据按照索引顺序存储,称为索引组织表(Index Organized Table)。 Memory引擎的数据和索引分开存储,数据以数组形式存放,主键索…...
Django交易商场
Hello,我是小恒不会java 最近学习django,写了一个demo,学到了不少东西。 我在GitHub上开源了,提示‘自行查看代码,维护,运行’。 最近有事,先发布代码了,我就随缘维护更新吧 介绍: 定…...

华为校园公开课走入上海交大,鸿蒙成为专业核心课程
4月12日,华为校园公开课在中国上海交通大学成功举办,吸引了来自计算机等相关专业的150余名学生参加。据了解,由吴帆、陈贵海、过敏意、吴晨涛、刘生钟等教授在中国上海交通大学面向计算机系本科生开设的《操作系统》课程,是该系学…...

【会员单位】泰州玉安环境工程有限公司
中华环保联合会理事单位 水环境治理专业委员会副主任委员单位 我会为会员单位提供服务: 1、企业宣传与技术项目对接; 2、企业标准、行业标准制定; 3、院士专家指导与人才培训 4、国际与国内会议交流 5、专精特新、小巨人等申报认证 6…...
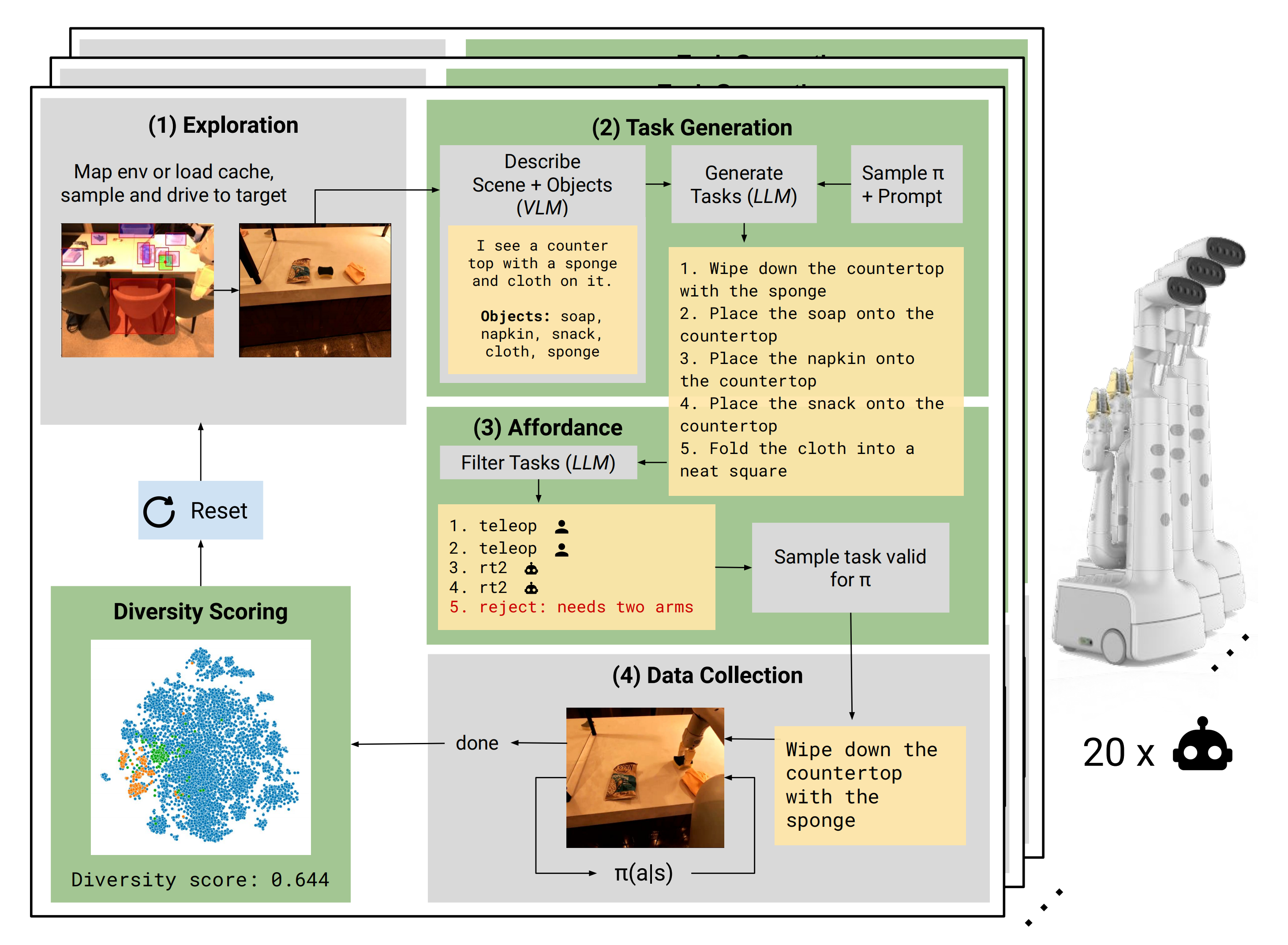
Google视觉机器人超级汇总:从RT、RT-2到AutoRT/SARA-RT/RT-Trajectory、RT-H
前言 随着对视觉语言机器人研究的深入,发现Google的工作很值得深挖,比如RT-2 想到很多工作都是站在Google的肩上做产品和应用,Google真是科技进步的核心推动力,做了大量大模型的基础设施,服(推荐重点关注下Googl…...
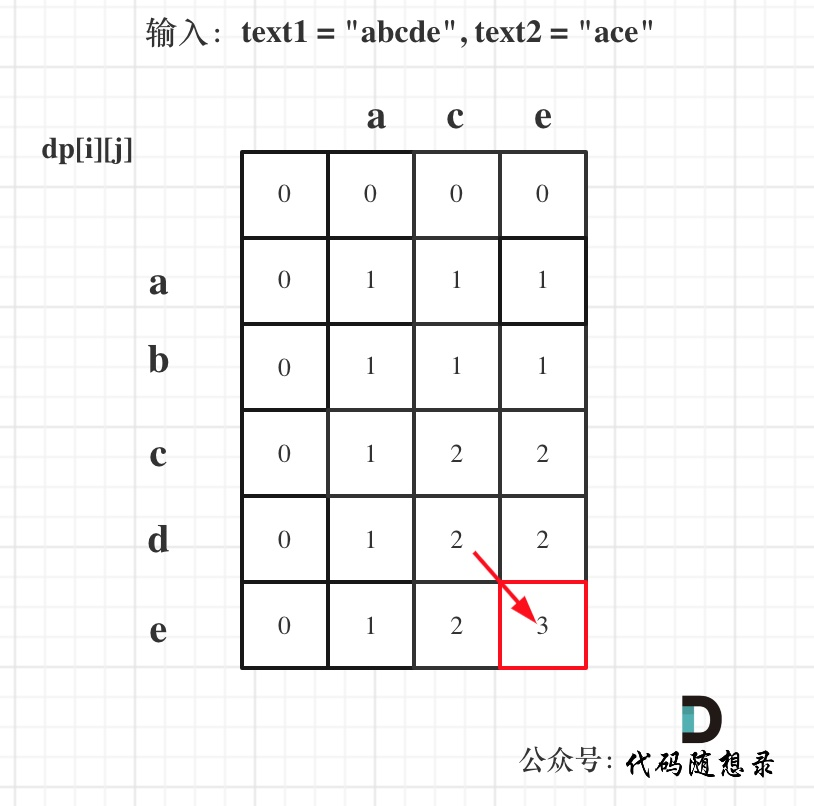
LeetCode-1143. 最长公共子序列【字符串 动态规划】
LeetCode-1143. 最长公共子序列【字符串 动态规划】 题目描述:解题思路一:动规五部曲解题思路二:1维DP解题思路三:0 题目描述: 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。…...
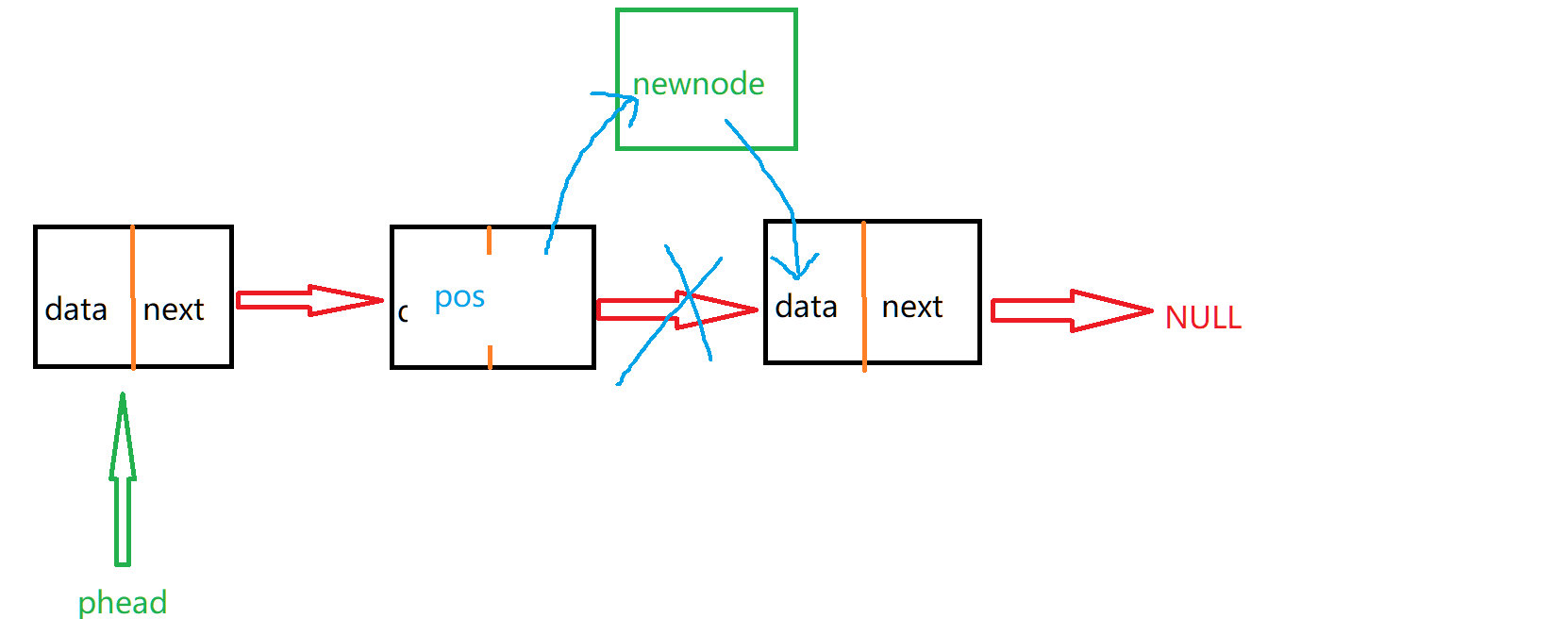
从0开始创建单链表
前言 这次我来为大家讲解链表,首先我们来理解一下什么是单链表,我们可以将单链表想象成火车 每一节车厢装着货物和连接下一个车厢的链子,单链表也是如此,它是将一个又一个的数据封装到节点上,节点里不仅包含着数据&…...

STC89C52学习笔记(十)
STC89C52学习笔记(十) 综述:本文介绍了DS18B20和单总线协议,以及讲述了如何使用DS18B20测量温度。 一、单总线协议 1.只有一根通讯线:DQ (常见的运用单总线的两种设备:DS18B20和DHT11&#…...
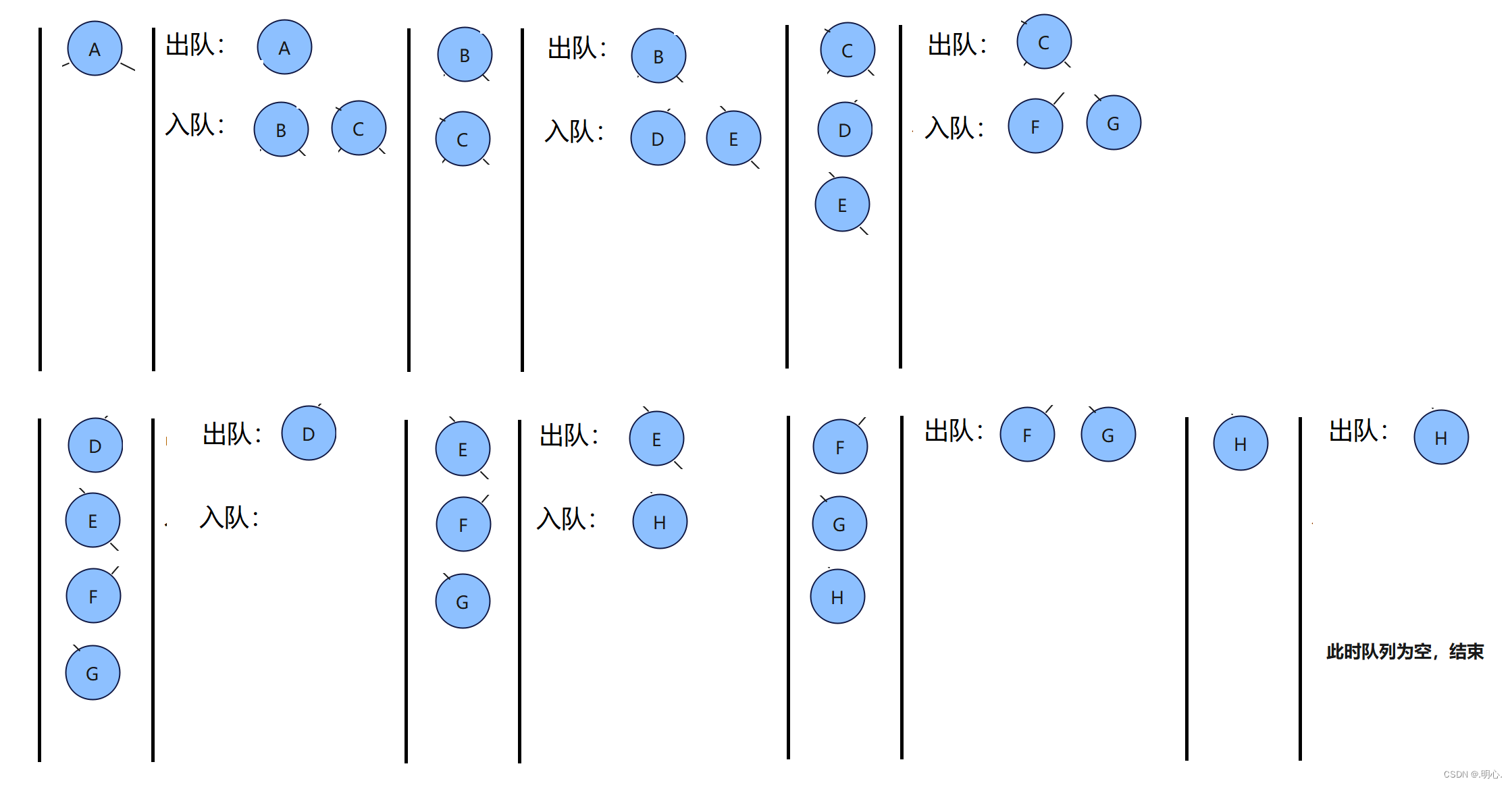
初识二叉树和二叉树的基本操作
目录 一、树 1.什么是树 2. 与树相关的概念 二、二叉树 1.什么是二叉树 2.二叉树特点 3.满二叉树与完全二叉树 4.二叉树性质 相关题目: 5.二叉树的存储 6.二叉树的遍历和基本操作 二叉树的遍历 二叉树的基本操作 一、树 1.什么是树 子树是不相交的;…...

如何开辟动态二维数组(C语言)
1. 开辟动态二维数组 C语言标准库中并没有可以直接开辟动态二维数组的函数,但我们可以通过动态一维数组来模拟动态二维数组。 二维数组其实可以看作是一个存着"DataType []"类型数据的一维数组,也就是存放着一维数组地址的一维数组。 所以&…...
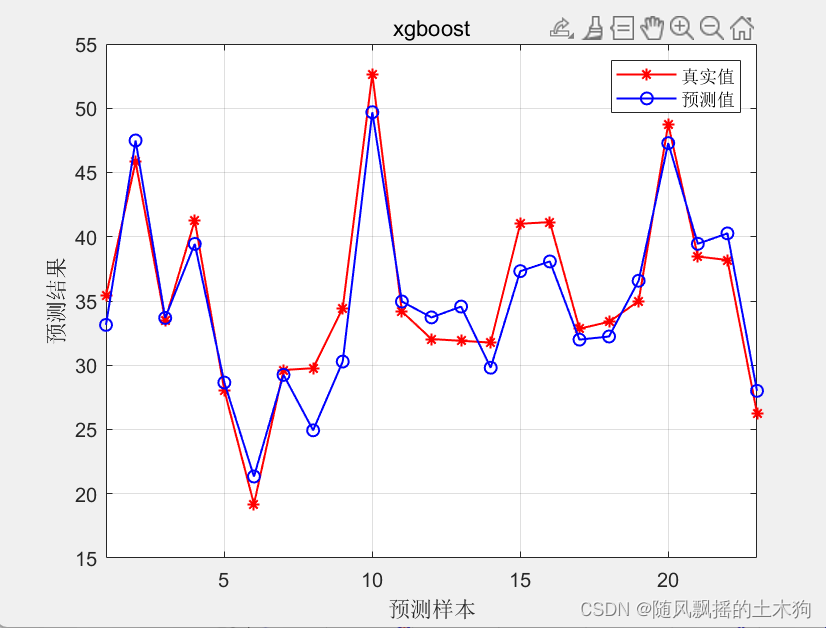
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型)
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型) 因matlab的xgboost训练模型不含敏感性分析算法,本文通过使用single算法,即单特征因素对输出影响进行分析,得出不同…...

C语言程序与设计——工程项目开发
之前我们已经了解了C语言的基础知识部分,掌握这些之后,基本就可以开发一些小程序了。在开发时,就会出现合作的情况,C语言是如何协作开发的呢,将在这一篇文章进行演示。 工程项目开发 在开发过程中,你接到…...

【Java核心技术】第6章 接口
1 接口 接口不是类,而是对希望符合这个接口的类的一组需求 1.1 Comparable 接口 要对对象进行比较,就要实现(implement)比较(comparable)接口 注意: implements Comparable<Manager> Comparable接口是泛型接口 class Manager exten…...

【Java探索之旅】从输入输出到猜数字游戏
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java编程秘籍 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、输入输出1.1 输出到控制台1.2 从键盘输入 二、猜数字游戏2.1 所需知识:…...

【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II
【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II 解法 ---------------🎈🎈题目链接🎈🎈------------------- 解法 😒: 我的代码实现> 动规五部曲 ✒️确定dp数组以及下标的含义 dp[j]表示容量为…...

2023 年上海市大学生程序设计竞赛 - 四月赛
A. 宝石划分 A. 宝石划分 - 2023 年上海市大学生程序设计竞赛 - 四月赛 - ECNU Online Judge 找距离N最近的M的因数q,输出M/q 如果是暴力所的话,会超时 #include <bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(false)…...

别让这6个UI设计雷区毁了你的APP!
一款成功的APP不仅仅取决于其功能性,更取决于用户体验,这其中,UI设计又至关重要。优秀的UI设计能够为用户带来直观、愉悦的交互体验,甚至让用户“一见钟情”,从而大大提高产品吸引力。 然而,有很多设计师在…...

继承【C/C++复习版】
目录 一、什么是继承?怎么定义继承? 二、继承关系和访问限定符? 三、基类和派生类对象可以赋值转换吗? 四、什么是隐藏?隐藏vs重载? 五、派生类的默认成员函数? 1)派生类构造函…...

题目 2694: 蓝桥杯2022年第十三届决赛真题-最大数字【暴力解法】
最大数字 原题链接 🥰提交结果 思路 对于每一位,我我们都要尽力到达 9 所以我们去遍历每一位, 如果是 9 直接跳过这一位 如果可以上调到 9 我们将这一位上调到 9 ,并且在a 中减去对应的次数 同样的,如果可以下调到 9,我…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
