纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录
- 数学
- 质因数分解
- 辗转相除法求最大公约数
- 最小公倍数:
- 快速幂
- 乘法逆元
- 费马小定理
- 逆元
- 乘法逆元
- 素数判定与埃式筛法
- 朴素素数判定法
- 埃式筛法
- 图论
- 并查集T3:真题--合根植物
- Dijkstra
- Floyd
- 基础算法
- 递归,循环,前缀和,差分
- STL
数学
质因数分解
int reduce(int prime[],int pn,int n,int rest[]){int i,k=0;for(i=0;i<pn;i++){if (n==1) break;if (prime[i]*prime[i]>n) {rest[k++]=n;break;}while(n%prime[i]==0){n/=prime[i];rest[k++]=prime[i];}}return k;}
解析:
这段代码是一个名为reduce的函数,它接受四个参数:一个整数数组prime[],一个整数pn表示数组的长度,一个整数n和一个整数数组rest[]。函数的目的是将整数n分解为质因数,并将这些质因数存储在rest[]数组中。
函数首先初始化两个变量i和k,其中i用于循环遍历prime[]数组,k用于记录rest[]数组的索引。
接下来,函数使用一个for循环遍历prime[]数组。在每次迭代中,它首先检查n是否等于1,如果是,则跳出循环。然后,它检查当前质数的平方是否大于n,如果是,则将n添加到rest[]数组中,并跳出循环。
如果当前质数的平方不大于n,则进入一个while循环。在这个循环中,只要n能被当前质数整除,就将n除以当前质数,并将当前质数添加到rest[]数组中。这个过程会一直重复,直到n不能被当前质数整除为止。
最后,函数返回k,即rest[]数组中的元素个数。
#include<bits/stdc++.h>
using namespace std;int main()
{int n,i;cin>>n;cout<<n<<"=";for(i=2;i<=n;i++){while(n!=i){if(n%i==0){cout<<i<<"*";n=n/i;}elsebreak;}}cout<<n<<endl;return 0;
}
辗转相除法求最大公约数
inline int gcd(int a,int b)
{if(a%b==0)return b;elsereturn (gcd(b,a%b));
}
- 简单写法:
int gcb(int a,int b){return b==0 ? a:gcb(b,a%b);}
最小公倍数:
int lcm(int a,int b){return a/gcd(a,b)*b;//防溢出 , 很妙啊 ,大家可以记一下
}
快速幂

- 模板
int qmi(int a,int b,int p)//对p取模
{int res=1;while(b)//只要b不为0,就一直迭代下去 {if(b&1)res=res*a%p;//b为奇数,乘一个a到答案里a=a*a%p,b>>=1;//底数平方,指数除以2 }return res; }
- 例题:数的幂次–1181
#include<bits/stdc++.h>
using namespace std;using ll =long long;ll qmi(ll a,ll b,ll p)//对p取模
{ll res=1;while(b)//只要b不为0,就一直迭代下去 {if(b&1)res=res*a%p;//b为奇数,乘一个a到答案里a=(ll)a*a%p,b>>=1;//底数平方,指数除以2 }return res; } int main(){int t;cin>>t;while(t--){ll n,m,p;cin>>n>>m>>p;cout<<qmi(n,m,p)<<endl;}return 0;}
乘法逆元
费马小定理

逆元

乘法逆元
- 例题1:求乘法逆元
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
int t,n;
ll p=1e9+7;
ll qsm(ll a,ll b)
{ll res=1;while(b){if(b&1) res=res*a%p;a=a*a%p;b>>=1;}return res%p;
}
ll inv(ll x)
{return qsm(x,p-2);
}
int main()
{cin>>t;while(t--){cin>>n;cout<<inv(n)<<endl;}return 0;
}- 例题2:获胜的概率–3932
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=1e9+7;
ll kmi(ll a,ll b)
{ll res=1;while(b){if(b&1) res=res*a%p;a=a*a%p;b>>=1;}return res%p;}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);ll n,k;cin>>n>>k;if(k==0){cout<<1<<endl;for(int i=2;i<=n;i++) cout<<0<<endl;}else if(k&1){for(int i=1;i<=n;i++){if(i&1) cout<<0<<endl;else cout<<kmi(n/2,p-2)<<endl;}}else{for(int i=1;i<=n;i++){if(i&1) cout<<kmi((n+1)/2,p-2)<<endl;else cout<<0<<endl;}}return 0;}素数判定与埃式筛法
朴素素数判定法

- 例题:疑似素数-3334
#include<bits/stdc++.h>
using namespace std;
//求和
int f(int x)
{int res=0;while(x)res+=x%10,x/=10;return res;}
bool isPrime(int n)
{if(n<2)return false;for(int i=2;i<=n/i;i++){if(n%i==0)return false;}return true;}
int main()
{int n;cin>>n;int ans=0;for(int i=1;i<=n;i++){if(isPrime(f(i)))ans++;}cout<<ans<<endl;
}
埃式筛法
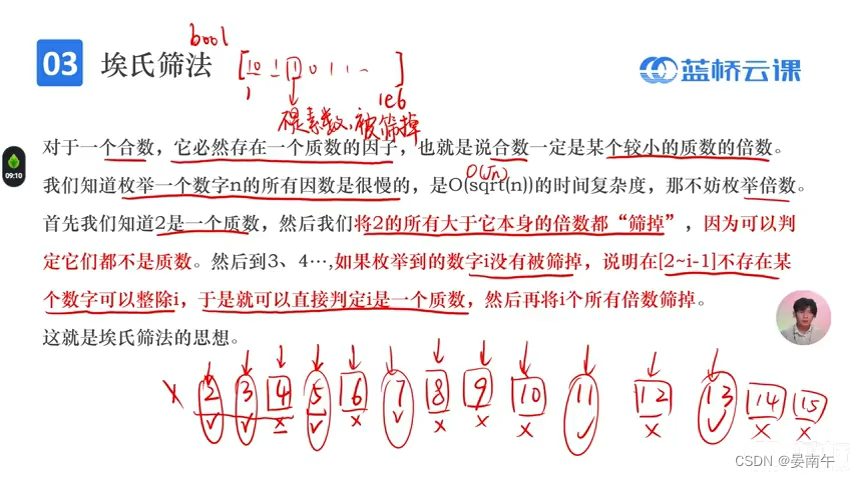
bool vis[N];
vis[0]=vis[1]=true;//被筛掉了
for(int i=2;i<=n;i++)
{if(!vis[i])//如果i没有被筛掉,那么进行枚举for(int j=2*i;j<=n;j+=i)//枚举倍数 ,每次j变成i的倍数vis[j]=ture; }
- 例题2:小明的素数对–3205
#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
bool shai[N];vector<int> vec;//将素数筛中杂乱的质数变成排列有序的一个集合,用vector
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,ans=0;cin>>n;shai[0]=shai[1]=1;for(int i=2;i<=n;i++){if(!shai[i]){vec.push_back(i);for(int j=2*i;j<=n;j+=i) shai[j]=1;}}for(int i=0;i<vec.size();i++)for(int j=i+1;j<vec.size();j++){if(!shai[vec[j]-vec[i]]) ans++;}cout<<ans;return 0;}图论
并查集T3:真题–合根植物
- 并查集模版题:
- 注意:不要调用string库。
- 什么是并查集:处理不相交集合的合并问题。
- 用途:求连通子图,求最小生成树的Kruskal算法和求最近公共祖先等。
- 操作:
-
初始化:

-
查询与合并:

-
查询时对路径进行压缩:
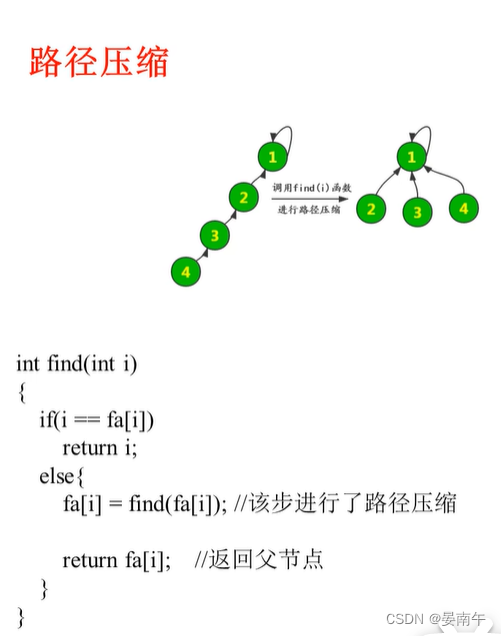
-
例题

-
#include<cstdio>
#include<cstdlib>
using namespace std;
// 开始的时候定义数组
#define MAXN 20001
int fa[MAXN];
//最好不要这样定义// 初始化
void init(int n)
{for(int i=0;i<=n;i++)fa[i]=i;}
// 查询 int find(int x){
// 递归出口if(x==fa[x])return x;else{fa[x]==find(fa[x]);return fa[x];}}
// 合并
void unionn(int i,int j)
{int i_fa=find(i);// 找到i的祖先 int j_fa=find(j);// 找到j的祖先 fa[i_fa]=j_fa ;//i的祖先指向j的祖先 }
// 写主函数
int main()
{int m,n,x,y,q;scanf("%d",&n);init(n);// 初始化这个数组scanf("%d",&m); //有m行for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);unionn(x,y);} scanf("%d",&q);// 输入q行 for(int i=1;i<=q;i++){scanf("%d%d",&x,&y);if(find(x)==find(y))printf("YES\n");elseprintf("NO\n");}return 0; }
- 合根植物题解:这道题只有一个返回值,所以查询的时候注意不要增加一个返回值了。
#include<stdio.h>
int fa[1000005];
//初始化void init(int n){for (int i=1;i<=n;i++)fa[i] = i;}// 查询
int find(int x)
{if (fa[x] != x){int sx = find(fa[x]);fa[x] = sx;}return fa[x];
}// 合并void unionn(int i,int j){int i_fa=find(i);int j_fa=find(j);fa[i_fa]=j_fa;}
int main(void)
{int m,n,q;scanf("%d%d%d",&m,&n,&q);init(m*n); int x,y;for(int i=0;i<q;i++){scanf("%d%d",&x,&y);unionn(x,y);}//计数器的设置int ans=0;for(int i=1;i<=m*n;i++){if(i==fa[i]){//一个数等于链条的祖先ans++; } }printf("%d\n",ans);return 0;
}
Dijkstra


Floyd

基础算法
递归,循环,前缀和,差分
添加链接描述
STL
添加链接描述

相关文章:

纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录 数学质因数分解辗转相除法求最大公约数最小公倍数:快速幂乘法逆元费马小定理 逆元乘法逆元素数判定与埃式筛法朴素素数判定法埃式筛法 图论并查集T3:真题--合根植物DijkstraFloyd 基础算法递归,循环,前缀和,差分STL 数学…...

python 最简单的网页爬虫
import requests url"https://news.ifeng.com/c/8OZc7eV01sM" rrequests.get(url) print(r.status_code) print(r.iter_lines()) # 获取响应的内容 content r.text# 打印网页内容 print(content) # responser.json() # print(response) 爬虫知识讲解: …...

二叉树-数据结构
二叉树-数据结构 二叉树是属性结构的一个重要类型。 如下图二叉树形状 二叉树特征如下: 1.二叉树由 n(n > 0) 个节点组成 2.如果 n 为 0,则为空树 3.如果 n 1,则只有一个节点称为根节点(root) 4.每个节点最多有两个节点,节…...

ansible使用shell模块的环境变量问题
在本机写了一个shell脚本,关于操作mysql的,在本机执行脚本可以正常操作数据库,脚本运行正常。 但是使用ansible ansible -i ./hosts test_teledb -m copy -a "src/etc/ansible/scripts/check.sh dest/tmp"ansible -i ./hosts test…...

ChatGPT论文写作指南:写出引人注目的论文
ChatGPT无限次数:点击直达 ChatGPT论文写作指南:写出引人注目的论文 作为一名有着10年经验的专业CSDN网站原创文章优质创作者,在当今的信息爆炸时代,论文写作的重要性愈发显现。如何能够写出引人注目的论文,吸引读者的眼球并获得…...
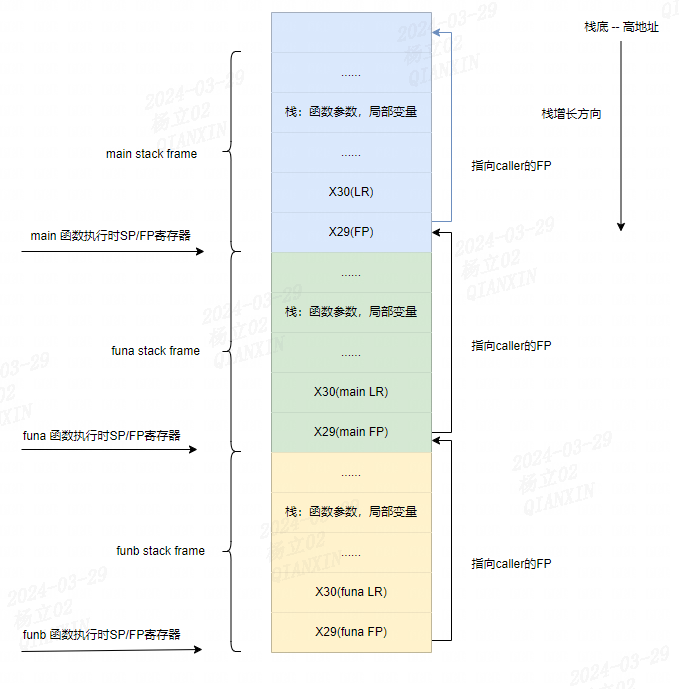
ARM64架构栈帧回溯
文章目录 前言一、栈帧简介二、demo演示 前言 请参考:ARM64架构栈帧以及帧指针FP 一、栈帧简介 假设下列函数调用: funb() {func() }funa() {funb() }main() {funa() }main函数,funa函数,funb函数都不是叶子函数,其…...
-- 基础知识)
LangChain:大型语言模型(LLMs)-- 基础知识
1、LangChain的调用大型语言模型模块的介绍 LangChain是一个强大的框架,旨在通过调用大型语言模型(LLM)来开发各种语言驱动的应用程序。在LangChain中,LLM不仅仅是一个简单的模型调用,而是一个复杂链条中的关键部分。…...

总分410+专业130+国防科技大学831信号与系统考研经验国防科大电子信息与通信工程,真题,大纲,参考书。
好几个学弟催着,总结一下我自己的复习经历,希望大家复习少走弯路,投入的复习正比换回分数。我专业课831信号与系统130(感觉比估分要低,后面找Jenny老师讨论了自己拿不准的地方也没有错误,心里最近也这经常回…...

chatgpt Team 4.0共享合租账号的新方式
为了更好地满足工作需求,我订阅了GPT PLUS会员,但我发现,4.0每三小时问答40次经常吃灰,而且每月近200元的费用让我感到有点肉痛。 于是,我开始寻找有没有什么替代品。在逛某论坛的时候,发现了一个共享Team…...

类和对象二
一、运算符重载 为了使自定义类型可以使用加减等运算符,CPP提供了一个功能叫运算符重载。 关键字:operator操作符 运算符重载最好定义在类对象里,这也可以避免访问不到私有成员的问题。 代码演示: 在类里定义之后,…...

GD32 HID键盘矩阵键盘发送数据时,一直发送数据问题处理
这个问题找了两三天,开始并不认为是示例程序的问题,只是感觉是自己代码问题。 这个解决流程大概是: 先调好矩阵键盘=> 调用发送函数。 就是因为调用时,一直发送数据,我也在按键抬起做了操作,始终不行。 最后,发现时示例代码中有个 空闲中断 引起的。 udev->reg…...

小程序地理位置权限申请+uniapp调用uni.getLocation
文章目录 一、小程序地理位置权限申请二、uniapp调用uni.getLocation 一、小程序地理位置权限申请 需要确保小程序类目已经填写 点击左侧导航栏找到最后的“设置”——“基本设置”——“前往填写” 在开发管理——接口设置——地理位置中可以看到: 即可点击想要申…...

后台权限控制及动态路由
需求 后台系统需要能实现不同的用户权限可以看到不同的功能。 用户只能使用他的权限所允许使用的功能。 功能设计 之前在我的SpringSecurity的课程中就介绍过RBAC权限模型。没有学习过的可以去看下 RBAC权限模型 。这里我们就是在RBAC权限模型的基础上去实现这个功能。 表分…...

云计算:Linux 部署 OVS 集群(控制端)实现OpenFlow
目录 一、实验 1.环境 2.Linux 部署 OVS 集群(控制端) 3.控制端对接服务端OVS网元 4.服务端OVS添加流表 5.服务端删除OVS 二、问题 1. ODL如何查找已安装插件 2.查看流表显示不全 3.如何删除OVS流表 一、实验 1.环境 (1) 主机 表1 宿主机 主…...

使用/api/put保存数据到OpenTSDB,报204错误
错误信息 HttpResponseProxy{HTTP/1.1 204 No Content [Content-Type: application/json; charsetUTF-8, Content-Length: 0]} 错误原因 在OpenTSDB中,使用/api/put保执行写入操作,得到204响应,表示已经成功写入数据库。...
)
Open3D kmeans聚类(马氏距离,Python版本)
文章目录 一、简介二、算法步骤三、代码实现四、实现效果参考资料一、简介 在诸多的聚类方法中,K-Means聚类方法是属于“基于原型的聚类”(也称为原型聚类)的方法,此类方法均是假设聚类结构能通过一组原型刻画,在现实聚类中极为常用。通常情况下,该类算法会先对原型进行初始…...

python抠图程序
import cv2 import numpy as np def color_threshold(image, lower, upper): hsv_image cv2.cvtColor(image, cv2.COLOR_BGR2HSV) mask cv2.inRange(hsv_image, lower, upper) result cv2.bitwise_and(image, image, maskmask) return result # 读取图片…...
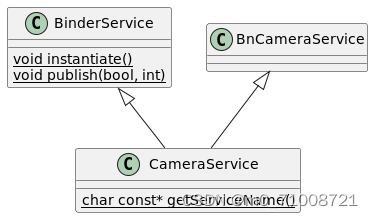
Android13 CameraServer启动流程
代码入口 frameworks/av/camera/cameraserver 里面包含了四个文件 我们先来看看Android.bp的内容 package {// See: http://go/android-license-faq// A large-scale-change added default_applicable_licenses to import// all of the license_kinds from "frameworks_a…...

如何升级node.js版本
升级Node.js可以通过多种方式来完成,以下是四种常见的方法: 方法一:使用Node.js官方安装程序 访问Node.js的官方网站,下载对应你操作系统的最新版本安装程序。通常,你可以 https://nodejs.org/en/download 找到你需…...
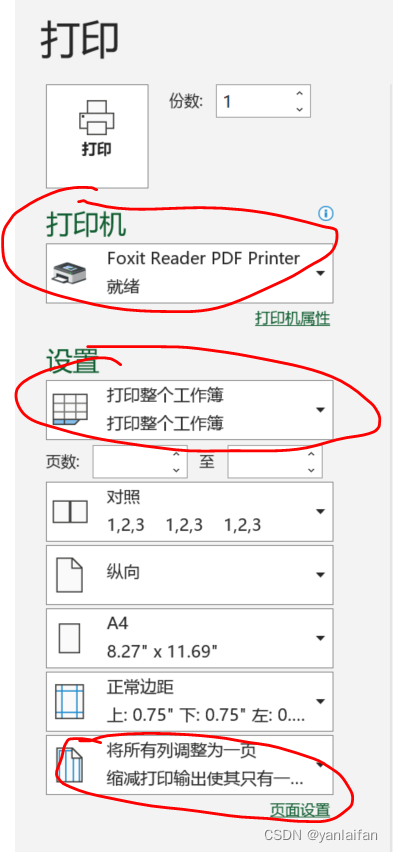
Excel---一个工作簿中的多个sheet合并成一个PDF
0 Preface/Foreword 1 操作方法 1.1 方法一 文件》 导出 》创建PDF/XPS 》 选项 》发布内容 》“整个工作簿” 1.2 方法二 文件》 打印》 打印机选项中,选择一种PDF阅读器 》设置选项中,选择打印整个工作簿。...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
