遍历列举俄罗斯方块的所有形状
以前玩俄罗斯方块的时候,就想过一个问题,为什么俄罗斯方块就这7种形状,还有没有别的形状?自己也在纸上画过,比划来比划去,确实就这几种形状。
继续思考一下,那假如是3个块组合的形状,有几种有效组合形式?
这个似乎不是太难,在纸上比划几下,应该能得出结果。
但是,如果是5个块组合起来,又有多少种有效的组合形式?
这就比较麻烦了,排列组合的可能性大增,不那么容易比划清楚。
从程序员的角度,这其实是一个遍历穷举的过程,所以有了这一篇文章。
首先也不搞太复杂的,先从3个块的组合开始尝试。
3个块的组合,考虑所有可能性,就是在3x3的一个区域里面,任意取点。然后添加一些限制条件,例如:
1,区域内点位不重复;
2,每个点都至少需要有一个相邻点;
3,平移不重复;
4,旋转不重复;
这4个条件是否充足了?
反正我开始时就是这么想的,认为充足了。当然,到后面遇到了问题,才又添加了个限制条件。
为了能方便的判断结果是否正确,将有效结果展示出来,是有必要的。
需要界面展示,这里选择了是要QT,毕竟有可移植性,在windows下开发,以后要移植到linux下也可以。
看一下,基本的布局界面是这样的:

左上角,是那个画出方块组合形状的区域。在遍历过程中,遇到有效的方块组合,就在下面区域中以一半的宽高比例画出来。
这里由于涉及到了方块组合的不同大小的展示,以及还有平移动作,就需要考虑方块的点坐标,不能存储实际的宽高值(例如:0,20,40),而是更抽象的基础比例(例如:0,1,2)。
下面是简要介绍实现过程,具体实现可从文末的下载地址去获取。
先定义方块的类:
class Block
{
public:QPoint leftUp;//左上角的坐标int width;//宽度int height;//高度QColor penColor;//铅笔的颜色QColor brushColor;//画刷的颜色
}再定义一个方块组合的类:
class BlockGroup
{
public:BlockGroup(int num);int blockNum;//方块的数目Block block[BLOCK_NUM];//方块的数组int flagValid;//有效标志
};一个穷举遍历的主要过程如下:
int pos[5];int pointTotal=pow(curBlock.blockNum,2);//一个点可以选择的位置int tryNum = pow(pointTotal,curBlock.blockNum);//每一个点,都有这么多种可能的位置,总的可能点位选择while(tickNum<tryNum){//遍历所有的可能性for(int i=0;i<curBlock.blockNum;i++){//将一个大数,分解为几个部分,每部分给一个方块使用,用作坐标赋值int pointLevel=pow(pointTotal,curBlock.blockNum-1-i);pos[i]=(tickNum/pointLevel)%pointTotal;}//计算,寻找有效的方块组合for(int j=0;j<curBlock.blockNum;j++){curBlock.block[j].leftUp.setX((x+pos[j]/curBlock.blockNum)*w);curBlock.block[j].leftUp.setY((y+pos[j]%curBlock.blockNum)*h);curBlock.block[j].width = w;curBlock.block[j].height = h;curBlock.block[j].penColor = Qt::black;curBlock.block[j].brushColor = Qt::yellow;}if(checkPosValid(&curBlock)!=1){//内部有点位重复,此种组合无效,跳过tickNum+=1;continue;}if(checkAdjacent(&curBlock)!=1){//检测每点都有相邻点,若不是,跳过tickNum+=1;continue;}if(checkConnectivity(&curBlock)!=1){//检测组块内部的连通性,若不是,跳过tickNum+=1;continue;}//规范坐标adjustCoordinates(&curBlock);int flagRepeat=0;for(auto it=blockGroupList.begin();it!=blockGroupList.end();it++){if(checkTranslationRepeatability(&(*it),&curBlock)){//发现是平移重复的flagRepeat=1;break;}if(checkRotaltionalRepeatability(&(*it),&curBlock)){//发现是旋转重复的flagRepeat=1;break;}}if(flagRepeat==1){tickNum+=1;continue;}//新的有效方块组合,存入结果链表中blockGroupList.push_back(curBlock);//写文件writeBlockInfo(&curBlock);//设置标志,通知画出 flagFlush=1;update();break; }下面逐个展示循环里面调用的方法。
检查方块组合中的点位是否重复:
//检测块内点位是否有效(不能重复)
int BlockDialog::checkPosValid(BlockGroup *blockInfo){for(int k=0;k<blockInfo->blockNum-1;k++){for(int i=k+1;i<blockInfo->blockNum;i++){if(blockInfo->block[k].leftUp==blockInfo->block[i].leftUp){return 0;}}}return 1;
}检查不是孤立点位:
//检测两点是否相邻
int BlockDialog::checkNearPoint(QPoint *point1,QPoint *point2,int w,int h){QPoint pointRight=QPoint(w,0);QPoint pointDown=QPoint(0,h);if(*point1+pointRight == *point2){//右邻return 1;}if(*point1 == *point2+pointRight){//左邻return 1;}if(*point1+pointDown == *point2){//下邻return 1;}if(*point1 == *point2+pointDown){//上邻return 1;}return 0;//不相邻
}
//检测有相邻块
int BlockDialog::checkAdjacent(BlockGroup *blockInfo){int isNearNum=0;for(int i=0;i<blockInfo->blockNum;i++){isNearNum=0;for(int k=0;k<blockInfo->blockNum;k++){if(k!=i){if(1==checkNearPoint(&blockInfo->block[k].leftUp, &blockInfo->block[i].leftUp,blockInfo->block[i].width,blockInfo->block[i].height)){isNearNum++;}}}if(isNearNum==0){//没有相邻点return 0;}}return 1;
}已经检查过不是孤立点了,为什么还要检查点的连通性(checkConnectivity)?
这就是前面说过的那个添加的限制条件。为什么呢?
前面列举了4个限制条件,在应用到3个方块组合时没有遇到问题,但是在穷举4个方块的组合的时候就遇到了问题,例如下面这种方块组合,竟然是满足条件的:

然而,这并不是我期望的形状,我希望所有方块都是相连通的。没有孤立方块,这个条件没有包含所有方块连通的要求,所以,还需要增加一个限制条件:
5,要保证所有方块是连通起来的。
如下代码是检测方法:
//检测块内连通性
int BlockDialog::checkConnectivity(BlockGroup *blockInfo){int isNearNum=0;//将块组各点位信息赋值到节点中Node *nodeArray=new Node[blockInfo->blockNum];for(int i=0;i<blockInfo->blockNum;i++){nodeArray[i].point = blockInfo->block[i].leftUp;}//设置相邻节点for(int i=0;i<blockInfo->blockNum;i++){for(int j=0;j<blockInfo->blockNum;j++){if(i!=j){setNearNode(&nodeArray[i],&nodeArray[j]);}}}//从节点0开始,进行遍历DepthFirstSearch(&nodeArray[0]);//检查是否有未遍历到的结点for(int i=0;i<blockInfo->blockNum;i++){if(1==nodeArray[i].isChecked){isNearNum++;} else {break;//有未走到的点,即组块有未连通部分}}delete[] nodeArray;if(isNearNum==blockInfo->blockNum){//完成遍历,即方块组是连通的return 1;}return 0;
}这里调用了一个函数 DepthFirstSearch() ,是深度优先搜索算法。
这里涉及到图的连通性,参考这个链接,讲得比较清楚:
https://blog.csdn.net/weixin_44122303/article/details/122924246
//深度优先搜索--遍历相邻节点
void DepthFirstSearch(Node *node){if(node==NULL){return;}//递归调用,注意避免无限循环!if(node->isChecked==1){//已经检查过的,不要再进行检查了,避免无限循环!return;}//设置检查标志node->isChecked=1;//递归调用,检查相邻点DepthFirstSearch(node->up);DepthFirstSearch(node->down);DepthFirstSearch(node->left);DepthFirstSearch(node->right);return ;
}这里还有一个规范坐标的函数 adjustCoordinates(&curBlock); 为什么需要它?
也是在遇到问题之后才知道的。
在平移比较方块组合是否是重复的情况时,发现明明是一样的形状,却判断为不重复。
细细分析之后,发现是顺序不同,例如如下情况:
(0,1,2)与(0,2,1)
都是3个直线相邻的方块,但是由于顺序不同,直接按逐点比较的话,属于不同的组合。所以,添加一个规范点位顺序的方法:
//规范坐标
//1,左上平移;
//2,按顺序存放:从左上角开始,先第一排,从左往右;然后第二排
int BlockDialog::adjustCoordinates(BlockGroup *blockInfo){//定位左上角方块的坐标QPoint leftTopPoint1(0,0);QPoint leftTopPoint2=getLeftTopBoundary(blockInfo);//1,对整个方块组进行平移int leftShift = leftTopPoint2.x()-leftTopPoint1.x();int upShift = leftTopPoint2.y()-leftTopPoint1.y();QPoint pointShift(leftShift,upShift);Block blockTmp=Block();list<Block> listBlock={};for(int i=0;i<blockInfo->blockNum;i++){blockTmp.leftUp=blockInfo->block[i].leftUp-pointShift;blockTmp.penColor=blockInfo->block[i].penColor;//进行块组的赋值,注意不能遗漏颜色属性blockTmp.brushColor=blockInfo->block[i].brushColor;listBlock.push_back(blockTmp);}//2,排序 -- 按什么顺序排列的?//重载Block的比较操作符: 顺序定义:从左上角开始,先第一排,从左往右;然后第二排listBlock.sort();int blockPos=0;for(auto it=listBlock.begin();it!=listBlock.end();it++){blockInfo->block[blockPos]=*it;blockPos++;}return 0;
}这里的排序方法,依赖的是比较操作,先比较点位的纵坐标y,再比较横坐标x:
bool operator<(const Block& block1) const{if(this->leftUp.y()<block1.leftUp.y()){return true;} else if(this->leftUp.y()==block1.leftUp.y()){if(this->leftUp.x()<block1.leftUp.x()){return true;}}return false;}再就是平移重复检测:
//检测平移重复性
int BlockDialog::checkTranslationRepeatability(BlockGroup *blockInfo1,BlockGroup *blockInfo2)
{//逐点进行坐标比较for(int i=0;i<blockInfo2->blockNum;i++){if(blockInfo1->block[i].leftUp!=blockInfo2->block[i].leftUp){//坐标不同return 0;}}return 1;//重复
}最后是旋转重复检查,比平移重复检测复杂一点的是,有3次旋转(90度、180度、270度)。还有一点是旋转后的坐标如何确定,好在我在坐标系上比划了一下,旋转90度,就是(x,y) -> (y,-x),还是比较简单的:
//将方块组进行顺时针旋转90度
int BlockDialog::RotateBlockGroup(BlockGroup *blockInfo){//1,对整个方块组进行顺时针旋转90度Block blockTmp=Block();list<Block> listBlock={};for(int i=0;i<blockInfo->blockNum;i++){//旋转90度,就是(x,y) -> (y,-x)blockTmp.leftUp.setX(blockInfo->block[i].leftUp.y());blockTmp.leftUp.setY(0-blockInfo->block[i].leftUp.x());blockTmp.penColor=blockInfo->block[i].penColor;//进行块组的赋值,注意不能遗漏颜色属性blockTmp.brushColor=blockInfo->block[i].brushColor;listBlock.push_back(blockTmp);}//2,排序 -- 按什么顺序排列的?//重载Block的比较操作符: 顺序定义:从左上角开始,先第一排,从左往右;然后第二排listBlock.sort();//重新赋值int blockPos=0;for(auto it=listBlock.begin();it!=listBlock.end();it++){blockInfo->block[blockPos]=*it;blockPos++;}adjustCoordinates(blockInfo);//调整坐标,避免有负值坐标出现return 0;
}
//检测旋转重复性
int BlockDialog::checkRotaltionalRepeatability(BlockGroup *blockInfo1,BlockGroup *blockInfo2)
{for(int i=0;i<3;i++){//每次旋转90度,检查3次,加之前的一次平移检查,即完成了360度的检查//1,对方块组旋转90度,就是(x,y) -> (y,-x)RotateBlockGroup(blockInfo2);//2,先进行平移检测if(1==checkTranslationRepeatability(blockInfo1,blockInfo2)){return 1;}}return 0;
}至此,就实现了循环遍历所有方块组合的主体功能。
然后,将相关信息写入文件即可。
完整的代码可在如下链接地址获取:
修改代码中方块组合中方块的个数:
#define BLOCK_NUM 5 //4 //3 方块组内包含的方块个数可以遍历获取不同个方块的组合类型。
相关文章:

遍历列举俄罗斯方块的所有形状
以前玩俄罗斯方块的时候,就想过一个问题,为什么俄罗斯方块就这7种形状,还有没有别的形状?自己也在纸上画过,比划来比划去,确实就这几种形状。 继续思考一下,那假如是3个块组合的形状࿰…...
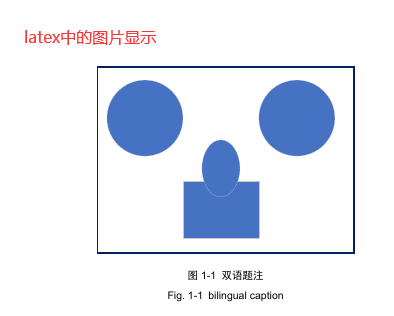
将Visio绘图导出PDF文件,使其自适应大小,并去掉导入Latex的边框显示
问题描述 将Visio绘图导成pdf文件,首先在Visio绘图如下: 如果直接导出或者另存为pdf文件,则会发现pdf文件是整个页面大小,而不是图片大小。而且在导入latex等排版工具现实时,会显示边框。 问题解决 1.调整Visio中的页…...
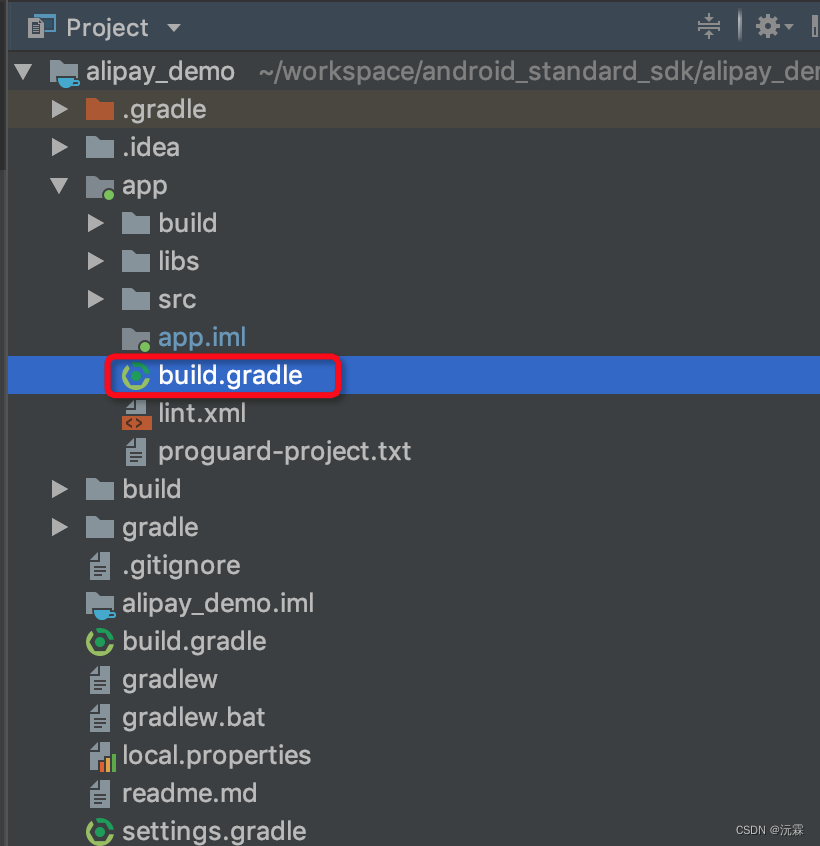
android支付宝接入流程
接入前准备 接入APP支付能力前,开发者需要完成以下前置步骤。 本文档展示了如何从零开始,使用支付宝开放平台服务端 SDK 快速接入App支付产品,完成与支付宝对接的部分。 第一步:创建应用并获取APPID 要在您的应用中接入支付宝…...

Mac 下 Python+Selenium 自动上传西瓜视频
背景 研究下 PythonSelenium 自动化测试框架,简单实现 Mac 下自动化批量上传视频西瓜视频并发布,分享给需要的同学(未做过多的异常处理)。 脚本实现 首先通过手工手机号登录,保存西瓜视频网站的 cookie 文件 之后加载…...
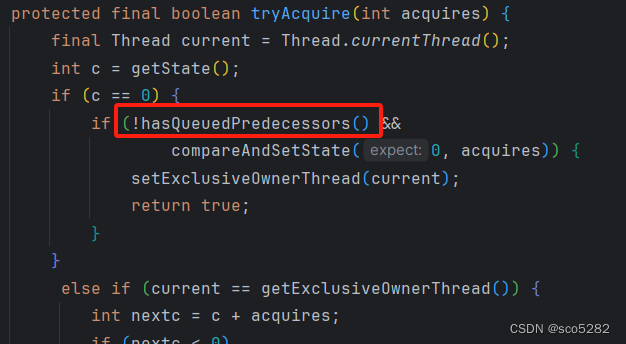
六:ReentrantLock —— 可重入锁
目录 1、ReentrantLock 入门2、ReentrantLock 源码解析2.1、构造方法:默认为非公平锁2.2、三大内部类2.2、lock():加锁【不可中断锁】2.2.1、acquire() 方法 —— AQS【模板方法】2.2.2.1 tryAcquire() 方法 —— AQS,由子类去实现2.2.2.2. a…...
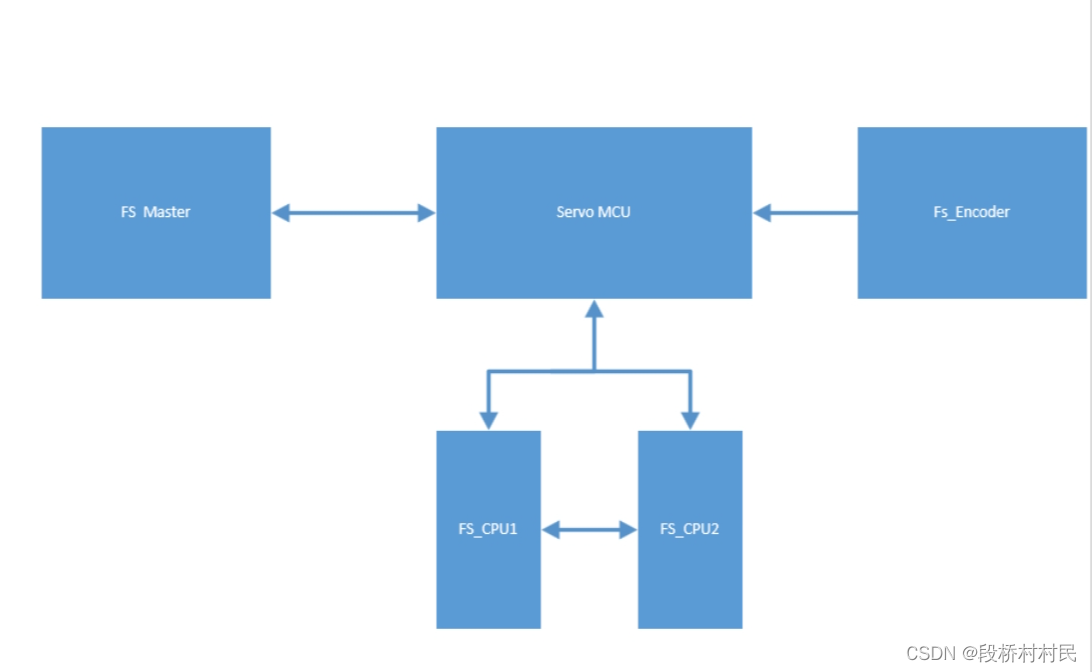
一种驱动器的功能安全架构介绍
下图提供了驱动器实现安全功能的架构 具有如下特点: 1.通用基于总线或者非总线的架构。可以实现ethercat的FSOE,profinet的profisafe,或者伺服本体安全DIO现实安全功能。 2.基于1oo2D架构,安全等级可以达到sil3。 3.高可用性。单…...

紫光展锐T610平台_4G安卓核心板方案定制开发
紫光展锐T610核心板配备Android 11操作系统,采用12nm制程工艺。该处理器CPU由2颗基于Cortex-A75架构的大核心和6颗基于Cortex-A55架构的小核心组成,最高主频为1.8GHz。GPU采用的是614.4MHz的Mali G52,可以流畅播放2400*1080分辨率视频&#x…...
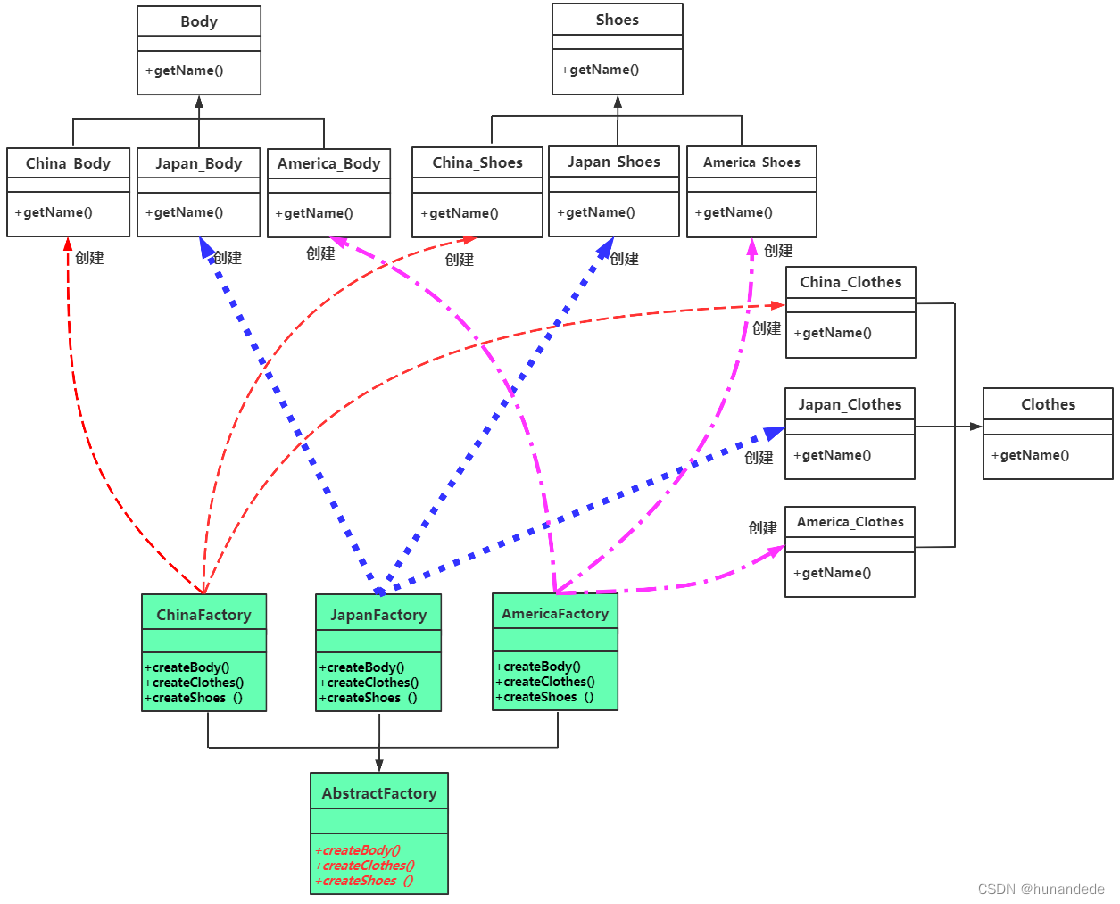
C++11 设计模式4. 抽象工厂(Abstract Factory)模式
问题的提出 从前面我们已经使用了工厂方法模式 解决了一些问题。 现在 策划又提出了新的需求:对于各个怪物,在不同的场景下,怪物的面板数值会发生变化, //怪物分类:亡灵类,元素类,机械类 …...

第8周 Python面向对象编程刷题
单击题目,直接跳转到页面刷题,一周后公布答案。加入QQ群701657573,随时答疑交流。 218:类对象属性219:坐标对象相加220:计算周长221:学生分数总和222:车辆类中创建引擎类对象223&am…...
【学习心得】神经网络知识中的符号解释②
我在上篇文章中初步介绍了一些神经网络中的符号,只有统一符号及其对应的含义才能使我自己在后续的深度学习中有着一脉相承的体系。如果对我之前的文章感兴趣可以点击链接看看哦: 【学习心得】神经网络知识中的符号解释①http://t.csdnimg.cn/f6PeJ 一、…...

Igh related:Small Bug And Notes Record.
Write at the top My computer got some silly problem with the typing software that my Chinese IM does’t work again. So I’ll try to record the things happened in English. If any error,DM me plz. BUGs BUG1 Undefined symbol Identifier “CLOCK_MONOTONIC”…...
)
【QT入门】Qt自定义控件与样式设计之qss介绍(Qt style sheet)
往期回顾: 【QT入门】 无边框窗口设计之实现圆角窗口-CSDN博客【QT入门】 无边框窗口设计综合运用之自定义标题栏带圆角阴影的窗口-CSDN博客 【QT入门】 无边框窗口设计之综合运用,实现WPS的tab页面-CSDN博客 【QT入门】Qt自定义控件与样式设计之qss介绍…...
-第49题:字母异位词分组)
[ LeetCode ] 题刷刷(Python)-第49题:字母异位词分组
题目描述 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词是由重新排列源单词的所有字母得到的一个新单词。 即将含有相同字符但排列顺序不同的字符串放入同一个组中。 示例 示例 1: 输入: strs ["eat", &qu…...

冒泡排序算法实现步骤
算法实现的过程: 1. 定义问题: - 算法是用来解决某一特定计算问题的方法步骤。例如,对于排序问题,我们需要一个算法对一组无序的整数进行排序。 2. 设计算法: - 冒泡排序是一种基础的排序算法。它的设计思路是…...

js实现webp转png/jpg
网上保存的图片是webp类型的,但是我把它嵌入flac格式的音频里后导致网页中无法播放 wps要会员,真麻烦。 完整代码: <!DOCTYPE html> <html lang"zh-CN"> <head> <meta charset"UTF-8">…...

DVWA -File Upload-通关教程-完结
DVWA -File Upload-通关教程-完结 文章目录 DVWA -File Upload-通关教程-完结页面功能LowMediumHighImpossible 页面功能 此页面的功能为选择某个图片文件点击Upload按钮上传,上传成功后得知文件上传路径为DVWA\hackable\uploads。 Low 源码审计 这段 PHP 代码…...

中介者模式:简化对象间通信的协调者
在面向对象的软件开发中,中介者模式是一种重要的行为型设计模式,用于降低多个对象间通信的复杂性。通过提供一个中心化的对象来处理不同组件之间的交互,中介者模式使得组件间不必显式引用彼此,从而使其松散耦合、更易于维护。本文…...

【Python系列】pydantic版本问题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
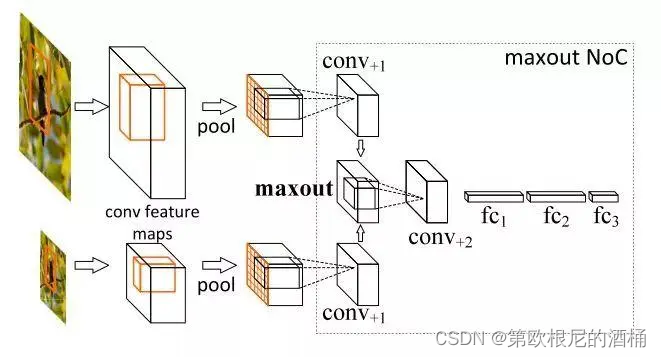
深度学习-多尺度训练的介绍与应用
一、引言 在当今快速发展的人工智能领域,多尺度训练已经成为了一种至关重要的技术,特别是在处理具有复杂结构和不同尺度特征的数据时。这种技术在许多应用中发挥着关键作用,例如图像识别、自然语言处理和视频分析等。 多尺度训练的定义 多尺…...

详解单文件组件
当你创建 Vue 单文件组件时,通常会包含三个部分:<template>、<script> 和 <style>。这三个部分分别用于定义组件的模板、逻辑和样式。让我更详细地解释一下它们的作用和用法: <template> <template> 标签用于…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
