计算机组成原理【CO】Ch2 数据的表示和应用
文章目录
- 大纲
- 2.1 数制与编码
- 2.2 运算方法和运算电路
- 2.3 浮点数的表示和运算
- 【※】带标志加法器
- OF
- SF
- ZF
- CF
- 计算机怎么区分有符号数无符号数?
- 【※】存储排列和数据类型转换
- 数据类型大小
- 数据类型转换
- 进位计数制
- 进制转换
- 2的次幂
- 各种码的基本特性
- 无符号整数的表示和运算
- 带符号整数的表示和运算
- 码之间的转换
- 移位运算
- 算数移位【针对有符号数】
- 逻辑移位【针对无符号数】
- 循环移位
- 乘除运算
- 无符号整数
- 有符号数
- 【※】IEEE754
- IEEE754浮点数与真值相互转化
- 由浮点数确定真值(阶码不是全0、也不是全1) :
- 浮点数的加减运算
- C强制类型转换
- 浮点数的规格化
大纲
2.1 数制与编码
- 王道书和大学教材讲到原码、补码时,使用了数学化的语言来讲解,不用过于深究,不是重点。计组这门课在考试中只考察应用,不考数学原理。对补码的数学原理感兴趣的同学,可以研究《数论》。
- 这个小节学起来难,但做起题来不算难。不建议反复死磕视频和王道书,可以先学一遍,然后直接做题,用“做题驱动复习”。
2.2 运算方法和运算电路
- 本节内容较多,一天的时间可能学不完。建议大家按照“伴学营打卡表”推荐的顺序做题,学一部分,做几道题。不建议一口气全部看完再去做题,那样一定消化不了。
- 对于没学过《数字电路》的同学,串行加法器、并行加法器的底层原理一定很难理解。不过没关系,考试不可能考太底层的电路设计。
- 带标志位的加法器是考试重点,也是经常结合第四章考察的重点,需要认真理解。OF、SF、ZF、CF 标志位的生成和作用一定要掌握。
- 乘法、除法的原理细节不容易理解,但考察频率较低,第一次学如果觉得难,也不建议花太多时间。只需要先建立起这个认知:在计算机硬件层面,无论是乘法还是除法,都是通过 加法、减法、移位运算 来实现的。
- C语言中各种数据类型的存储和相互转换、数据的存储和排列,这两部分内容很重要,经常结合大题考察,需认真理解。
2.3 浮点数的表示和运算
- 本节又是一块硬骨头,没什么好说的,学吧。第一次学难免让人怀疑人生,保持平常心尽力去学尽力去做题就好。第一次学习不建议死磕细节,得配合做题来体会这个部分怎么考,用“做题驱动复习”。
- 但很多同学的反馈是:“第一次学感觉很复杂,但第二轮回来复习感觉也没那么难”。原因是,本节内容虽难,但在经过做题训练之后,大家都会更清晰的认识到 “哪些地方是考试重点”、““哪些地方应该是我重点关注的”。
【※】带标志加法器
OF
- 有符号数的加减运算是否发生了溢出。
- OF=1时,说明发生了溢出
- OF=最高位产生的进位 ⊕ 次高位产生的进位
- OF位对无符号数的加减法无意义
SF
- 有符号数加减运算结果的正负性。
- SF=0表示运算结果为正数,SF=1表示运算结果为负数
- SF = 最高位的本位和(也是结果的最高位)
- SF位对无符号数的加减法无意义
ZF
- 表示运算结果是否为0。
- ZF=1表示运算结果为0,ZF=0表示运算结果非0
- 两个数的运算结果为n bit,只有n bit全为0时,ZF =1
- 对有符号、无符号都有意义
CF
-
进位、借位标志
-
表示无符号数的加减法是否发生了进位或借位
-
当CF=1时,说明无符号数的加减法发生了进位或借位,即发生了溢出
-
CF=最高位产生的进位⊕sub
- sub=1,表示减法
- sub=0,表示加法
-
CF位对有符号数的加减法无意义
-
有符号数的加减运算是否发生了溢出。
-
OF=1时,说明发生了溢出
-
OF=最高位产生的进位 ⊕ 次高位产生的进位
-
OF位对无符号数的加减法无意义

计算机怎么区分有符号数无符号数?
- 标志位会保存在PSW,ALU无法区分有符号数和无符号数,但由于计算机分为无符号加法和有符号加法。指令不同,执行时安排的微操作不同,从而区分有符号数和无符号数。
【※】存储排列和数据类型转换
数据类型大小
- char:1B
- short:2B
- int:4B
- float:4B
- long:4B
- double:8B
Tips:
- C语言中定点整数是用补码存储的
数据类型转换
整数之间转换(带符号和无符号之间)
- 长度相同
- 机器数不变,解释方式改变
- 短变长
- 先扩展:
- 无符号数补0
- 有符号数补符号
- 再解释
- 先扩展:
- 长变短
- 直接截断,只留下低位
- 再解释
整数与浮点数之间的转换
- 整数转浮点数:
- 先转换为2进制,写出科学记数法1.xxxx,再转为浮点数,截断尾部采用0舍1入的原则
- ⚠️可能精度丢失
- 浮点数转整数:
- 写出二进制小数,去掉小数部分,整数部分保留更低的位数
- ⚠️可能溢出、精度丢失
进位计数制
进制转换
- 二进制 <-> 八进制:每3个二进制位对应一个八进制位
- 二进制 <-> 十六进制:每4个二进制位对应一个十六进制位
- 【PS:整数部分前面补0,小数部分后面补0】
- 十进制 -> 进制
- 整数部分:除基取余法,先取得的“余”是整数的低位
- 小数部分:乘基取整法,先取得的“整”是小数的高位
2的次幂
| 次幂 | 2的次幂 |
|---|---|
| -4 | 0.0625 |
| -3 | 0.125 |
| -2 | 0.25 |
| -1 | 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
各种码的基本特性
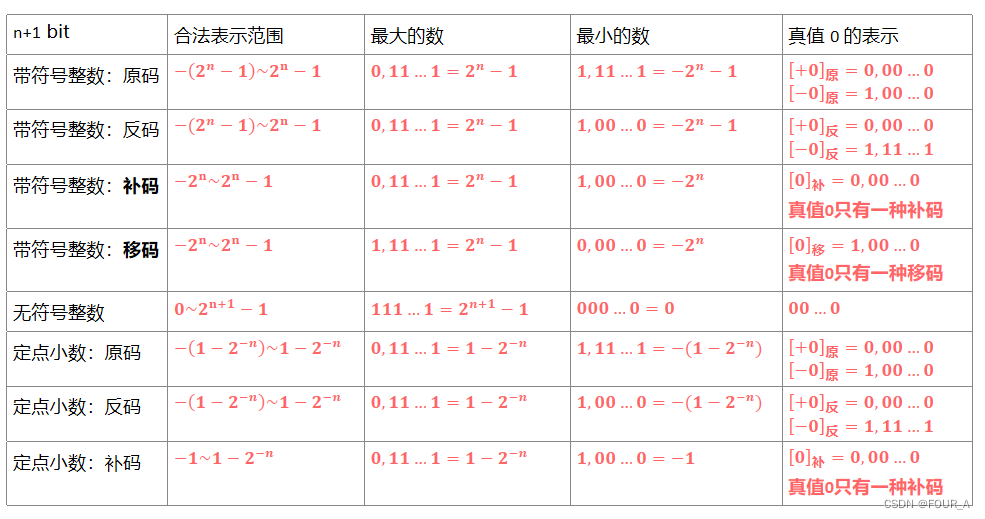
无符号整数的表示和运算
• 加法
• 全部位按位相加
• 减法
• x − y = x + [ − y ] x-y=x+[-y] x−y=x+[−y]
• [ − y [−y [−y]是 [ y ] [y] [y]从右往左第一个1的左边全部取反
• 溢出
• 手算:判断加减法的结果是否超出无符号数合法表示范围
• 机算: C F = 最高位进位 ⊕ S u b CF = 最高位进位 ⊕ Sub CF=最高位进位⊕Sub
带符号整数的表示和运算
Tips:
• 计算机内部,所有带符号整数的加减法都要先转换为补码
计算机硬件如何做带符号数补码的加法:
• 从最低位开始,所有位按位相加(符号位参与运算),并往更高位进位
计算机硬件如何做带符号数补码的减法:
• "被减数”不变,“减数”从右往左找到第一个1,这个1左边的全部位按位取反减法变加法
有符号数:
• 加法
• 按位相加
• 减法
• [ x ] 补 − [ y ] 补 = [ x ] 补 + [ − y ] 补 [x]_补 - [y]_补 = [x]_补 + [−y]_补 [x]补−[y]补=[x]补+[−y]补
• [ − y ] 补 是 [ y ] 补 [−y]_补 是 [y]_补 [−y]补是[y]补 从右往左第一个1的左边全部位按位取反
• 溢出
• 手算:判断加减法的结果是否超出有符号数合法表示范围
• 机算: O F = 最高位进位 ⊕ 次高位进位 OF = 最高位进位 ⊕ 次高位进位 OF=最高位进位⊕次高位进位
码之间的转换
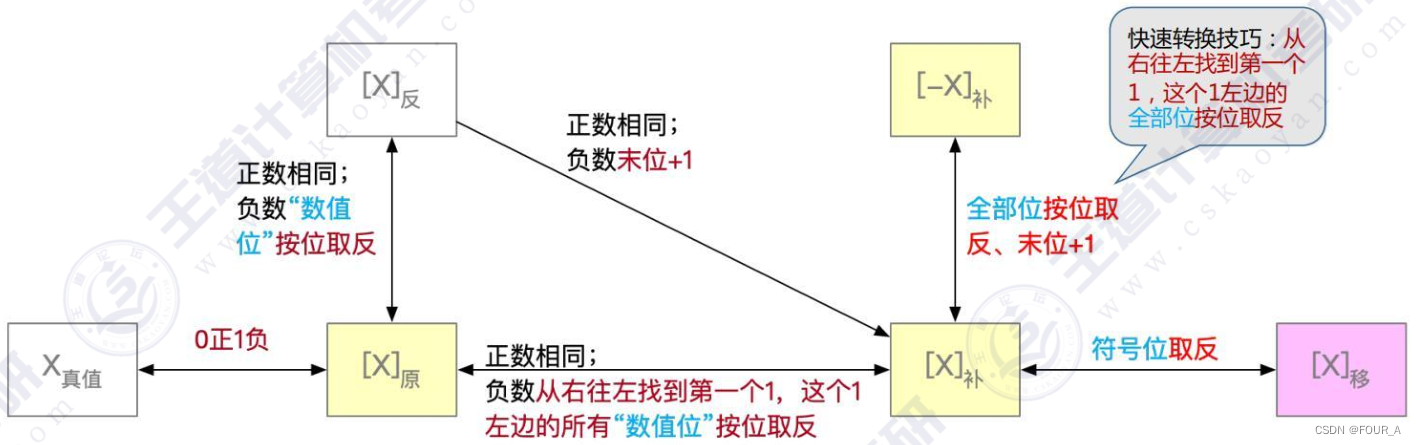
- [x]_移→[−x]_移:全部位按位取反,末位+1
- 使用补码表示时,若符号位相同,则数值位越大,码值越大
[ x ] 原 → [ x ] 反 ? [x]_原→[x]_反? [x]原→[x]反?
• 正数:不变
• 负数:符号位不变,数值位按位取反
[ x ] 原 ↔ [ x ] 补 ? [x]_原↔[x]_补? [x]原↔[x]补?
• 正数:不变
• 负数:符号位不变,从右往左找到第一个“1”,这个1左边的所有“数值位”按位取反
[ x ] 补 ↔ [ − x ] 补 ? [x]_补↔[−x]_补? [x]补↔[−x]补?
• 从右往左找到第一个“1”,这个1左边的全部位按位取反
[ x ] 补 ↔ [ x ] 移 ? [x]_补↔[x]_移? [x]补↔[x]移?
• 符号位取反
如何用补码快速计算真值:
- 直接在补码前面加上负号,再计算值
○ Eg: [ 1110 ] 补 = − 2 3 + 2 2 + 2 = − 2 [1110]_补 = −2^3 + 2^2 + 2 = −2 [1110]补=−23+22+2=−2
- 遇到一大串的1,将其看作符号位,直接化为最简,再用上述方法
○ Eg: [ 11111110 ] 补 = [ 10 ] 补 = − 2 [11111110]_补 = [10]_补 = −2 [11111110]补=[10]补=−2
如何快速求真值的补码:
eg: − 8190 = − 8192 + 2 = [ 1110 , 0000 , 0000 , 0010 ] 补 = E 002 H −8190 = −8192 + 2 = [1110,0000,0000,0010]_补 = E002H −8190=−8192+2=[1110,0000,0000,0010]补=E002H
移位运算
算数移位【针对有符号数】
- 左移1位相当于乘基数;右移1位相当于除基数,但由于位数有限,所以有时候算数移位并不能完全等效于乘除运算。
- 是针对有符号数:符号位保持不变。
- 正数:原码、反码、补码,无论左移还是右移都是补0
- 负数:
- 原码左移、右移都补0
- 反码左移和右移都补1
- 补码左移补0,右移补1
- 若采用双符号位来表示数,则最高符号位永远是真正的符号位,因此在算术移位时只有高符号位保留不变,低符号位要参与移位
逻辑移位【针对无符号数】
- 针对无符号数。符号位参与,左移、右移都补0,移出的位舍弃
循环移位
- 不带进位位
- 用移出的位补上空缺
- 带进位位
- 移出的位放到进位位,原进位位补上空缺
乘除运算
无符号整数
- 逻辑左移代替*2
- 溢出判断:
- n位乘n位,若用2n位保存乘积,则不会溢出
- n位乘n位,若用2n位保存中间结果,最后截取末尾n位作为最终的乘积,则可能溢出
- 当且仅当2n的前n位都是0时才不会溢出
有符号数
- 算术左移代替*2
- 溢出判断:
- n位乘n位,若用2n位保存乘积,则不会溢出
- n位乘n位,若用2n位保存中间结果,最后截取末尾n位作为最终的乘积,则可能溢出
- 当且仅当2n的前n+1位是全0或全1时才不会溢出
【※】IEEE754

IEEE754浮点数与真值相互转化
由浮点数确定真值(阶码不是全0、也不是全1) :
- 划分“某浮点数”,确定数符、阶码、尾数的分布
- 确定尾数1.M(注意补充最高的隐含位1)
- 确定 阶码的真值 = 移码 − 偏置值 阶码的真值 = 移码-偏置值 阶码的真值=移码−偏置值 (可将移码看作无符号数,用无符号数的值减去偏置值)
- ( − 1 ) s × 1. M × 2 ( E − 偏置值 ) (-1)^s × 1.M × 2^{(E - 偏置值)} (−1)s×1.M×2(E−偏置值)
浮点数的加减运算
对阶
- 目的:使两个操作数的小数点位置对齐
- 对阶操作只把较小的阶码调整到较大的阶码【所以不会引起阶码的上溢或下溢】
- 阶码增大,尾数右移
- 无阶码减小的情况【因为只用小阶向大阶对齐】
尾数求和
- 原码定点数的加减法
规格化
- 尾数规格化为1.xxxx的形式
舍入
- 舍入是浮点数概念,定点数无舍入
- 浮点数舍入的情况:对阶或者右规格化
- 舍入不一定产生误差(后几位为0时不产生误差)
溢出
- 尾数右规,阶码上溢,发生溢出异常
- 尾数左规,阶码下溢,当机器0处理
- 如果双符号位为01或10时,则溢出【第一个符号是真的符号】
- 10:正溢
- 01:负溢
- 尾数舍入可能引起阶码的上溢
- 尾数溢出时,结果不一定溢出

C强制类型转换
- 无损:
- char→int→long→double
- float→double
- 有损:
- int→float【可能会损失精度,float 的尾数数值位只有1+23位】
- float→int 【可能会溢出,也可能会损失精度,如小数转整数】
浮点数的规格化
- 规格化:规定尾数的最高数位必须是一个有效值(1)【即,基数为2时,要求尾数: 1 / 2 ≤ ∣ M ∣ < 1 1/2≤|M|<1 1/2≤∣M∣<1】
- 采用规格化浮点数的目的是为了增加数据的表示精度
- 负数补码的最高数值位是0,就是一个规定,不用纠结为什么
- 补码表示的最高位与尾数的符号位不同时,表示规格化了
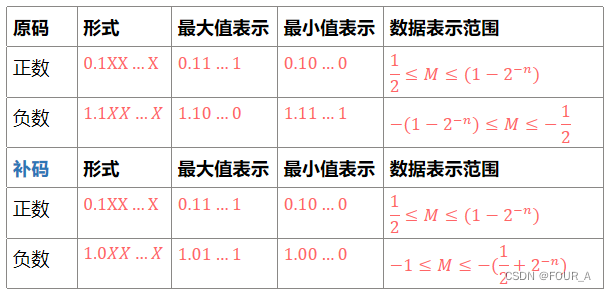
相关文章:

计算机组成原理【CO】Ch2 数据的表示和应用
文章目录 大纲2.1 数制与编码2.2 运算方法和运算电路2.3 浮点数的表示和运算 【※】带标志加法器OFSFZFCF计算机怎么区分有符号数无符号数? 【※】存储排列和数据类型转换数据类型大小数据类型转换 进位计数制进制转换2的次幂 各种码的基本特性无符号整数的表示和运算带符号整…...

dfs回溯 -- Leetcode46. 全排列
题目链接:46. 全排列 题目描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示…...
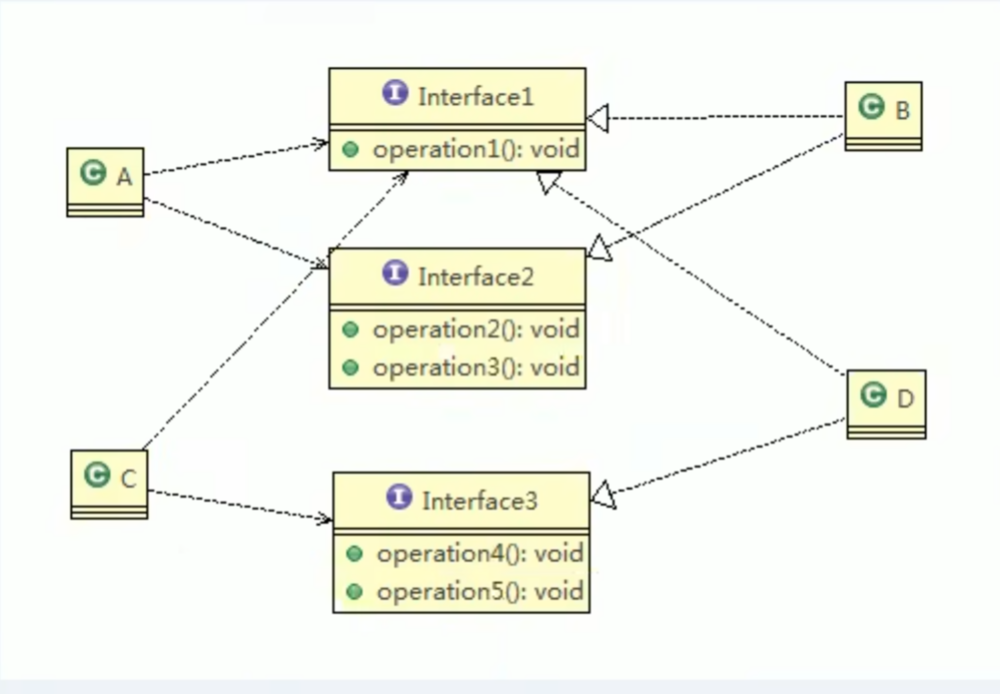
设计模式-接口隔离原则
基本介绍 客户端不应该依赖它不需要的接口,即一个类对另一个类的依赖应该建立在最小的接口上先看一张图: 类A通过接口Interface1 依赖类B,类C通过接口Interface1 依赖类D,如果接口Interface1对于类A和类C来说不是最小接口,那么类…...
BD202311夏日漫步(最少步数,BFS或者 Dijstra)
本题链接:码蹄集 题目: 夏日夜晚,小度看着庭院中长长的走廊,萌发出想要在上面散步的欲望,小度注意到月光透过树荫落在地砖上,并且由于树荫的遮蔽度不通,所以月光的亮度不同,为了直…...

React - 你知道props和state之间深层次的区别吗
难度级别:初级及以上 提问概率:60% 如果把React组件看做一个函数的话,props更像是外部传入的参数,而state更像是函数内部定义的变量。那么他们还有哪些更深层次的区别呢,我们来看一下。 首先说props,他是组件外部传入的参数,我们知道…...
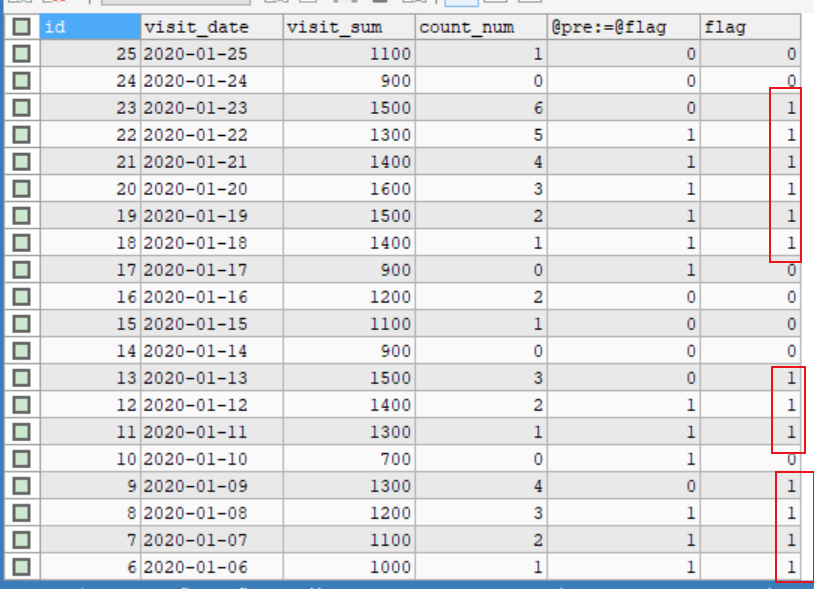
mysql 查询实战-变量方式-解答
对mysql 查询实战-变量方式-题目,进行一个解答。(先看题,先做,再看解答) 1、查询表中⾄少连续三次的数字 1,处理思路 要计算连续出现的数字,加个前置变量,记录上一个的值,…...

SpringBoot3配置SpringSecurity6
访问1:localhost:8080/security,返回:需要先认证才能访问(说明没有权限) 访问2:localhost:8080/anonymous,返回:anonymous(说明正常访问) 相关文件如下&…...
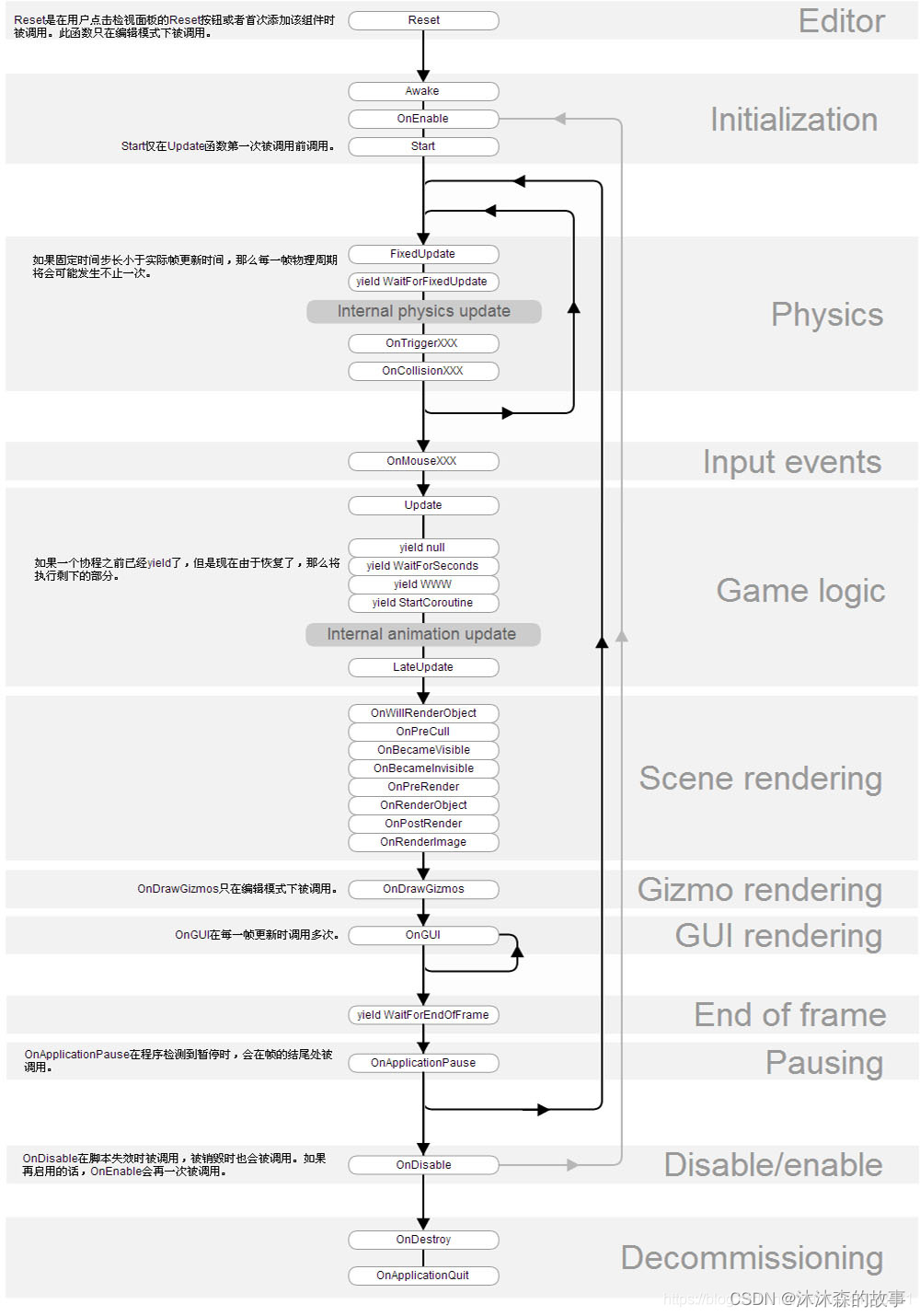
Unity之Unity面试题(三)
内容将会持续更新,有错误的地方欢迎指正,谢谢! Unity之Unity面试题(三) TechX 坚持将创新的科技带给世界! 拥有更好的学习体验 —— 不断努力,不断进步,不断探索 TechX —— 心探索、心进取…...
)
Linux命令-dos2unix命令(将DOS格式文本文件转换成Unix格式)
说明 dos2unix命令 用来将DOS格式的文本文件转换成UNIX格式的(DOS/MAC to UNIX text file format converter)。DOS下的文本文件是以 \r\n 作为断行标志的,表示成十六进制就是0D0A。而Unix下的文本文件是以\n作为断行标志的,表示成…...

企业怎么做数据分析
数据分析在当今信息化时代扮演着至关重要的角色。能够准确地收集、分析和利用数据,对企业的决策和发展都具有重要意义。数聚将介绍企业如何合理地利用数据分析,如何协助企业在竞争激烈的市场中取得优势。 一、建立完善的数据收集系统 在进行数据分析之…...

1111111111
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...
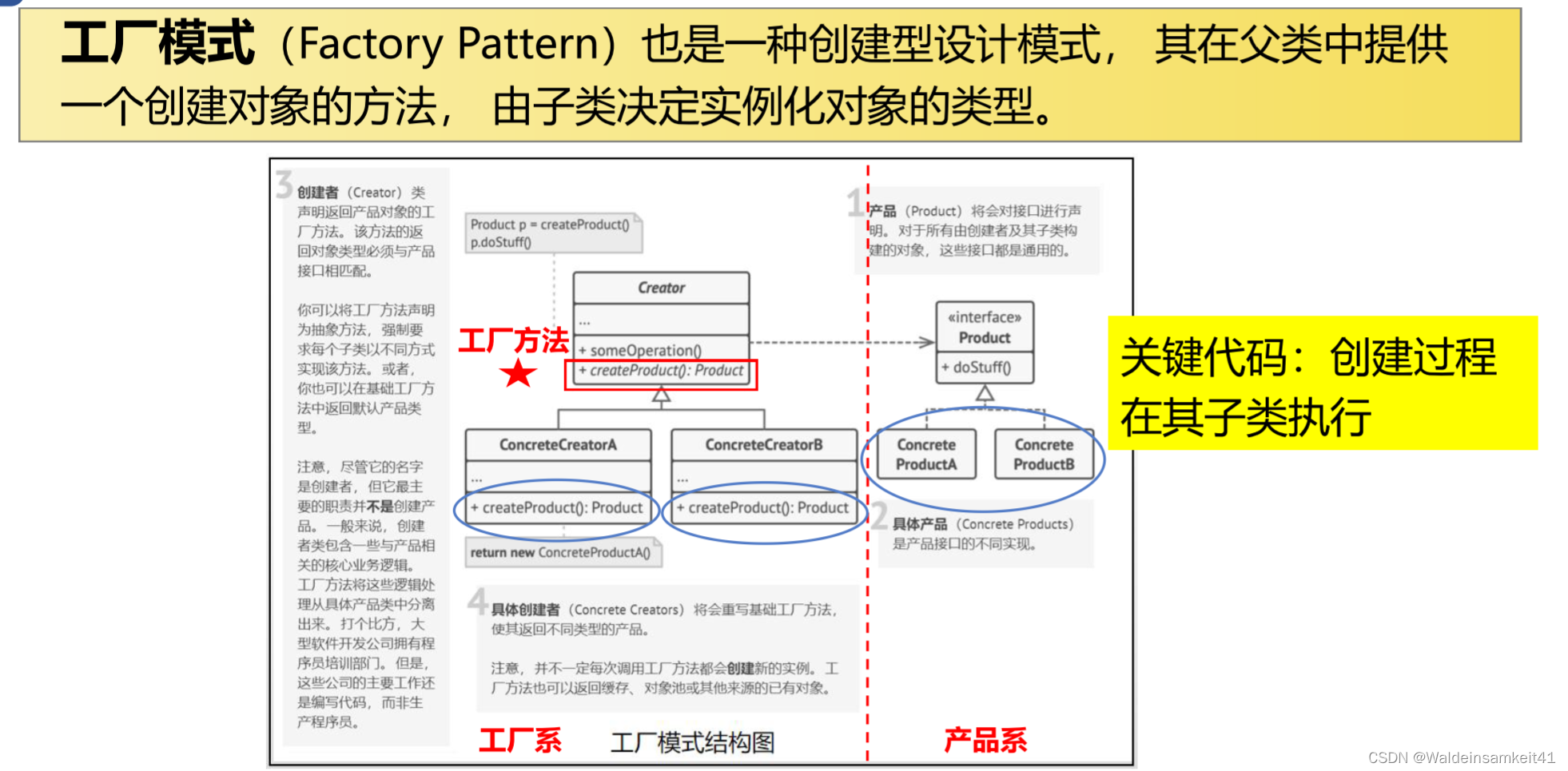
[面向对象] 单例模式与工厂模式
单例模式 是一种创建模式,保证一个类只有一个实例,且提供访问实例的全局节点。 工厂模式 面向对象其中的三大原则: 单一职责:一个类只有一个职责(Game类负责什么时候创建英雄机,而不需要知道创建英雄机要…...
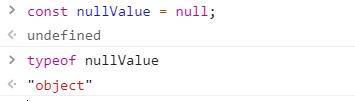
《前端防坑》- JS基础 - 你觉得typeof nullValue === null 么?
问题 JS原始类型有6种Undefined, Null, Number, String, Boolean, Symbol共6种。 在对原始类型使用typeof进行判断时, typeof stringValue string typeof numberValue number 如果一个变量(nullValue)的值为null,那么typeof nullValue "?" const u …...
【项目实战经验】DataKit迁移MySQL到openGauss(下)
上一篇我们分享了安装、设置、链接、启动等步骤,本篇我们将继续分享迁移、启动~ 目录 9. 离线迁移 9.1. 迁移插件安装 中断安装,比如 kill 掉java进程(安装失败也要等待300s) 下载安装包准备上传 缺少mysqlclient lib包 mysq…...
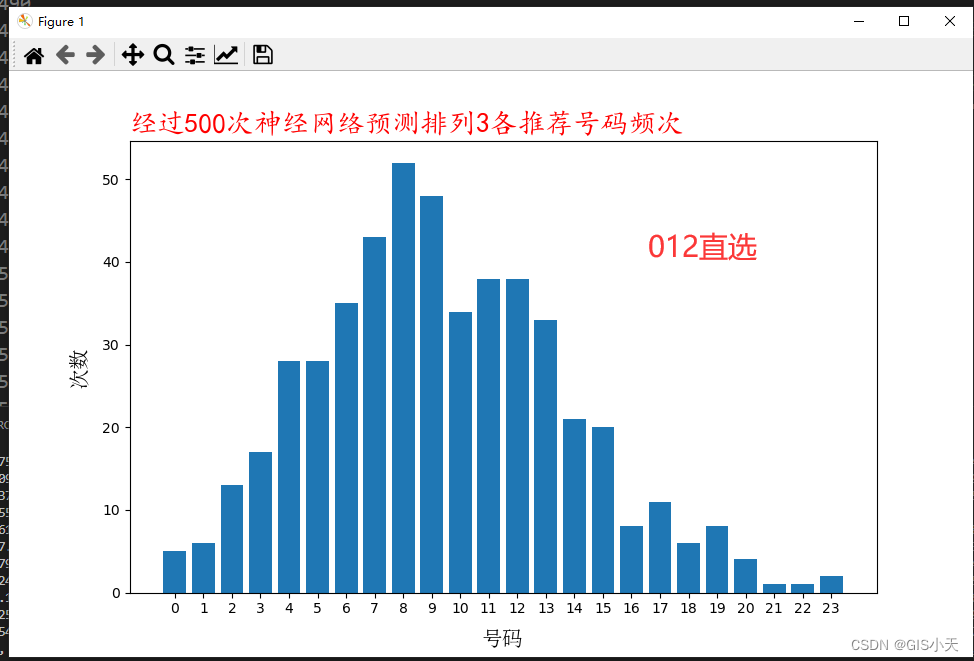
AI预测体彩排3第2弹【2024年4月13日预测--第1套算法开始计算第2次测试】
各位小伙伴,今天实在抱歉,周末回了趟老家,回来比较晚了,数据今天上午跑完后就回老家了,晚上8点多才回来,赶紧把预测结果发出来吧,虽然有点晚了,但是咱们前面说过了,目前的…...
2024年4月串讲题组一)
【13137】质量管理(一)2024年4月串讲题组一
目录 1.选择题 2.多选题 3.简答题 4.论述题 5.计算题 6.论述题 【13137】质量管理-速 记 宝 典【全国通用】</...

Go语言中工作负载类型对并发的影响
在实际工作开发中我们需要根据工作负载是CPU密集型还是I/O密集型,使用不同的方式来解决问题。下面我们先来看这些概念,然后再讨论其影响。 在程序执行时,工作负载的执行时间会受以下因素限制: CPU的速度--例如,运行归并排序算法。工作负载被称为CPU密集型。I/O速度--例如…...

常用的Python内置函数
目录 1. getattr() 函数: 2. setattr() 函数: 3. id():返回对象的唯一标识符(内存地址)。 4. type():返回对象的类型。 5. isinstance(obj, classinfo):判断对象是否是某种类型或其子类的实例。 6. issubclass(class1, class2):判断一个类是否是另一个类的子类。 …...

MAC(M1芯片)编译Java项目慢且发热严重问题解决方案
目录 一、背景二、排查三、解决四、效果以及结果展示五、总结 一、背景 使用idea编译项目等操作,经常性发热严重,并且时间慢。直到昨天编译一个项目用时30分钟,电脑温度很高,并且有烧灼的味道,于是有了此篇文章。 二、…...

如何循环pandas格式的数据
如何循环pandas格式的数据 要循环处理 Pandas 格式的数据,可以使用 iterrows() 方法或者 iteritems() 方法。 iterrows() 方法: import pandas as pd# 假设 df 是你的 Pandas DataFrame for index, row in df.iterrows():# 在这里处理每一行的数据&am…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
