二叉树练习day.9
669.修剪二叉搜索树
链接:. - 力扣(LeetCode)
题目描述:
给你二叉搜索树的根节点
root,同时给定最小边界low和最大边界high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]示例 2:
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]提示:
- 树中节点数在范围
[1, 104]内0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
思路:
与删除二叉树节点的思路一样,遍历二叉树,当前节点如果小于我们需要的区间,则删除该节点的左子树,并且去遍历当前节点的右子树,因为遍历的是二叉树搜索树,因此右子树的值肯定是大于根节点的,不确定右子树的所有元素都在我们需要的区间内,因此需要去遍历,当前节点如果大于我们需要的区间,则删除该节点的右子树,并且去遍历当前节点的左子树,查看是否所有的节点都满足我们的区间
递归实现:
1.确定函数参数和返回值,函数的参数一个为要修剪的二叉树,以及我们的区间范围,返回值应该是修剪后的二叉树
2.确定终止条件,如果当前节点为空,则返回上一个节点,否则查看当前节点的值是否满足我们的条件
3.确定单层递归逻辑,遍历左右子树
代码实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ struct TreeNode* trimBST(struct TreeNode* root, int low, int high) {if(!root)return NULL;if(root->val < low){struct TreeNode *tem = root->right;//遍历该节点的右子树,因为右子树比该节点大,但是不一定都在范围内tem = trimBST(root->right, low, high);free(root);return tem;}else if(root->val > high){//遍历该节点的左子树,因为左子树比该节点小,但是不一定都在范围内struct TreeNode *tem = root->left;tem = trimBST(root->left, low, high);free(root);return tem;}root->left = trimBST(root->left,low,high);root->right = trimBST(root->right,low,high);return root; }
108.将有序数组转换为二叉搜索树
链接:. - 力扣(LeetCode)
题目描述:
给你一个整数数组
nums,其中元素已经按 升序 排列,请你将其转换为一棵平衡
二叉搜索树。
示例 1:
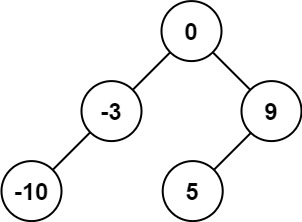
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
思路:
与构建二叉树的思路一样,对有序数组进行区间分割,先找到数组中间元素的位置,将其作为根节点,因为数组是递增的,且要构建搜索二叉树,如何按照区间分割的思路来实现
递归实现
1.确定函数的参数和返回值,函数参数应该为有序数组,以及我们要分割的左右区间
2.确定递归终止条件,如果我们数组的左右区间不符合正常情况,则返回空
3.确定单层递归逻辑,找到根节点位置,进行区间的分割,依次创建左右子树
代码实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ struct TreeNode *found(int *nums, int left, int right) {if(left > right)return NULL;struct TreeNode *node = (struct TreeNode*)malloc(sizeof(struct TreeNode));int mid = (left + right) / 2;node->val = nums[mid];node->left = found(nums,left,mid-1);node->right = found(nums,mid+1,right);return node; }struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {return found(nums,0,numsSize-1); }
538.把二叉搜索树转化为累加树
链接:. - 力扣(LeetCode)
题目描述:
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点
node的新值等于原树中大于或等于node.val的值之和。提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: . - 力扣(LeetCode) 相同
示例 1:
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]示例 2:
输入:root = [0,null,1] 输出:[1,null,1]示例 3:
输入:root = [1,0,2] 输出:[3,3,2]示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]提示:
- 树中的节点数介于
0和104之间。- 每个节点的值介于
-104和104之间。- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
思路:
根据二叉搜索树的性质,我们可以知道中序遍历(左中右)得到的是一个递增的数组,因为题目要求我们要得到累加树,因此我们就要从右子树开始访问再依次累加,因此我们的递归顺序就变为了右中左,在实现累加操作时,我们需要使用双指针的思路,一个记录当前节点,另一个记录前一个节点的值,用来实现累加
递归实现:
1.确定函数的参数和返回值,因为我们只是要对树每个节点的值进行操作,因此不需要返回值,传入的参数应该是二叉树
2.确定递归的终止条件,当我们二叉树遍历完成时,递归终止
3.确定单层递归逻辑,先去更新右子树,再去处理根节点,最后出来左子树
代码实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ int pre = 0; void fc(struct TreeNode *root) {if(root == NULL)return ;fc(root->right);root->val += pre;pre = root->val;fc(root->left); } struct TreeNode* convertBST(struct TreeNode* root) {pre = 0;fc(root);return root; }
相关文章:

二叉树练习day.9
669.修剪二叉搜索树 链接:. - 力扣(LeetCode) 题目描述: 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变…...

2024年第十七届“认证杯”数学中国数学建模网络挑战赛B题思路
B题 神经外科手术的定位与导航 人的大脑结构非常复杂,内部交织密布着神经和血管,所以在大脑内做手术具有非常高的精细和复杂程度。例如神经外科的肿瘤切除手术或血肿清除手术,通常需要将颅骨打开一个(或几个)圆形窗口,将病变部位暴露在术野中。但当病变部位较深时,就必…...
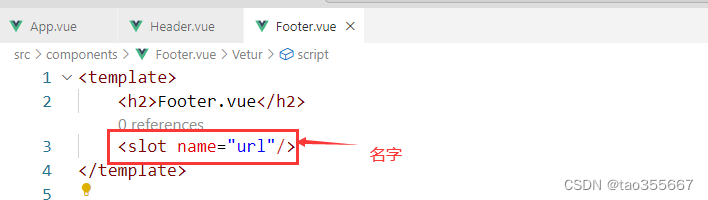
【vue】slot 匿名插槽 / 具名插槽
slot父组件向子组件传递数据 匿名插槽–直接写 具名插槽–指定名称 父组件中 子组件中: 代码 App.vue <template><h2>App.vue</h2><!-- 匿名插槽 --><Header><a href"1234567890.com">1234567890</a>&…...

FFmpeg: 自实现ijkplayer播放器-02环境搭建
文章目录 安装环境项目工程配置库文件 安装环境 IDE: Qt5.12 库: ffmpeg-4.2.1-win32SDL 项目工程配置 pro文件 TEMPLATE app TARGET SimpleIJKPlayer DESTDIR bin QT core gui widgets #CONFIG debug #DEFINES _UNICODE WIN64 QT_WIDGETS_LIBwin32 { LIBS -L$$PW…...
Redis从入门到精通(十七)多级缓存(二)Lua语言入门、OpenResty集群的安装与使用
文章目录 前言6.4 Lua语法入门6.4.1 初识Lua6.4.2 Hello World6.4.3 变量6.4.3.1 Lua的数据类型6.4.3.2 声明变量 6.4.4 循环6.4.5 函数6.4.6 条件控制 6.5 实现多级缓存6.5.1 安装和启动OpenResty6.5.2 实现ajax请求反向代理至OpenResty集群6.5.2.1 反向代理配置6.5.2.2 OpenR…...

pytest常用钩子函数
1、什么叫钩子函数 在Pytest框架中,钩子函数是一种允许用户扩展或者自定义测试执行过程的机制。钩子函数允许用户在测试的不同阶段插入自定义的代码,以实现特定的行为,操作或处理。这种插入式的机制使得Pytest具有高度的灵活性和扩展性。 如…...

.Net <% %>
<% %> 语法 : <% import namespace"system.data"%> 用来导入后台命名空间 指令用于指定当页和用户控件编译器处理 ASP.NET Web 窗体页 (.aspx) 和用户控件 (.ascx) 文件时所使用的设置。<% %> 语法 : <% name %> <% getstr() %&g…...

【C语言__编译和链接__复习篇2】
目录 前言 一、翻译环境和运行环境 二、翻译环境 2.1 预处理 2.1 编译 2.1.1 词法分析 2.1.2 语法分析 2.1.3 语义分析 2.2 汇编 2.3 链接 三、运行环境 四、简答主线问题 前言 本篇主要讨论以下问题: 主线问题: 1. 源文件(.c)如何转换成(.exe)文件…...

Jmeter —— 自动录制脚本
1、Jmeter配置 1.1新增一个线程组 1.2Jmeter中添加HTTP代理 1.3配置HTTP代理服务器 修改端口 修改Target Cintroller(目标控制器) 修改Grouping(分组) 编辑录制中的包含和排除 在“URL Patterns to include包含模式”中填入.*(123456).*用以过滤请求地址中不包含123456的请求…...

使用python互相转换AVI、MP4、GIF格式视频文件
一、AVI文件转MP4文件 要将AVI格式的视频转换为 MP4,你可以使用 Python的 moviepy 库。以下是一个示例代码,用于将 AVI 文件转换为 MP4 文件: from moviepy.editor import VideoFileClip# 读取 AVI 文件 clip VideoFileClip("input.a…...

11 Php学习:函数
PHP 内建函数Array 函数 PHP Array 函数是 PHP 核心的组成部分。无需安装即可使用这些函数。 创建 PHP 函数 当您需要在 PHP 中封装一段可重复使用的代码块时,可以使用函数。下面详细解释如何创建 PHP 函数并举例说明。 创建 PHP 函数的语法 PHP 函数的基…...

查询电脑用户名和组信息
在命令行里查看电脑名: c:\>hostname 在命令行里,查看组信息: # 显示本地所有的用户组 c:\>net localgroup #显示administrators组包含的用户信息 c:\>net localgroup administrators # 比如我的显示信息: C:\>ne…...
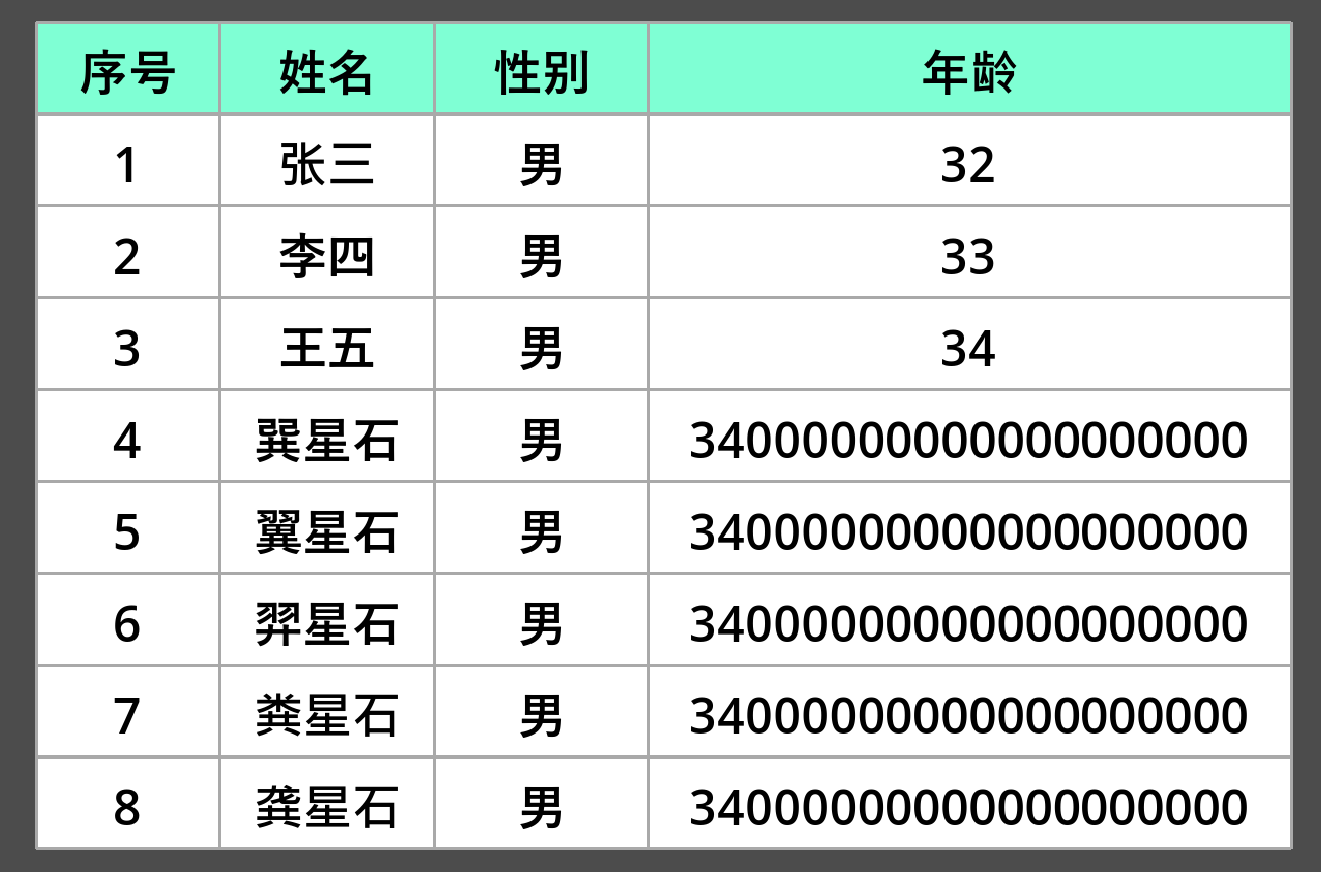
【Godot4.2】CanvasItem绘图函数全解析 - 9.绘制表格
概述 之前介绍TextLine和TextParagraph的时候,提到了用制表符和设定列宽形式来绘制简易表格,但是很明显,单纯使用此种方式很难获得对表格的精确控制。 所以对于表格绘制问题,我决定单独开坑,单独深入研究。 目前比较…...
部署HDFS集群(完全分布式模式、hadoop用户控制集群、hadoop-3.3.4+安装包)
目录 前置 一、上传&解压 (一 )上传 (二)解压 二、修改配置文件 (一)配置workers文件 (二)配置hadoop-env.sh文件 (三)配置core-site.xml文件 &…...

TCP协议简单总结
TCP:传输控制协议 特点:面向连接、可靠通信 TCP的最终目的:要保证在不可靠的信道上实现可靠的传输 TCP主要有三个步骤实现可靠传输:三次握手建立连接,传输数据进行确认,四次挥手断开连接 三次握手建立可靠…...

【Qt 实现录音】
Qt 实现录音源代码: #include <QAudioInput> #include <QAudioDeviceInfo> #include <QAudioRecorder> #include <QFile> #include...

python:算法竞赛入门之一
计算 斐波那契数列(Fibonacci sequence),不受长整型位数限制。 编写 fibonacci.py 如下 # -*- coding: utf-8 -*- """ 计算 斐波那契数列(Fibonacci sequence)""" import sys from …...
【大数据与云计算】虚拟机安装Linux
前言:使用Linux系统对大数据学习必不可少,本文主要介绍虚拟机安装linux的流程 文章目录 一、 下载VMware二、下载Linux三、安装Linux 一、 下载VMware 官网链接 下载VMware-player,一直下一步安装即可。 二、下载Linux 点击链接直接下载&…...

从零开始编写一个cmake构建脚本
简介 本文档介绍cmake构建脚本编写,包含的一些主要元素和命名规范。 cmake构建脚本编写步骤 cmake构建工具版本要明确 # 命令名字要小写,这条语句要求构建工具至少需要版本为3.12或以上 cmake_minimum_required (VERSION 3.12)工程名及库的版本号明确…...
pringboot2集成swagger2出现guava的FluentIterable方法不存在
错误信息 Description: An attempt was made to call a method that does not exist. The attempt was made from the following location: springfox.documentation.spring.web.scanners.ApiListingScanner.scan(ApiListingScanner.java:117) The following method did not ex…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...