蓝桥杯备考随手记: 常见的二维数组问题
在Java中,二维数组是一种可以存储多个元素的数据结构。它由多个一维数组组成,这些一维数组可以看作是行和列的组合,形成了一个矩阵。
1. 二维数组旋转问题
二维数组的旋转是指将数组中的元素按照一定规则进行旋转。通常有两种常见的旋转方式:顺时针旋转和逆时针旋转。
对于一个二维数组, 旋转操作可以分为以下几个步骤:
- 先将二维数组转置(即行列互换)
- 然后将每一行(顺时针)或每一列(逆时针)逆序
下面以顺时针旋转进行演示:
如果原始数组为:
1 2 3
4 5 6
7 8 9
转置后的数组为:
1 4 7
2 5 8
3 6 9
逆序每一行后的数组为:
7 4 1
8 5 2
9 6 3
这两个操作结合起来就实现了二维数组的旋转操作。
下面使用代码分别实现顺时针与逆时针旋转二维数组的操作:
顺时针旋转
public static void rotate(int[][] matrix) {int n = matrix.length; // 获取二维数组的大小,即行数或列数// Step 1: 转置操作for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]的值int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// Step 2: 行逆序操作for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n - 1 - j]的值int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}}
}
逆时针旋转
public static void antiRotate(int[][] matrix) {int n = matrix.length; // 获取二维数组的大小,即行数或列数// Step 1: 转置操作for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]的值int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// Step 2: 列逆序操作for (int i = 0; i < n / 2; i++) {for (int j = 0; j < n; j++) {// 交换matrix[i][j]和matrix[n - 1 - i][j]的值int temp = matrix[i][j];matrix[i][j] = matrix[n - 1 - i][j];matrix[n - 1 - i][j] = temp;}}
}
2. 二维数组找规律问题
二维数组数据的找规律是通过观察数组中的元素,寻找其中的规律或者模式。
以下是一些常见的二维数组数据找规律的方法和技巧:
-
观察元素的位置关系:通常情况下,二维数组中的元素有着特定的位置关系,如递增或递减的行索引或列索引、对角线上的元素等。通过观察这些位置关系,可以发现其中的规律。
-
分析元素的数值变化:观察数组中元素的数值变化可以帮助我们找到其中的规律。例如,数组中的元素可能按照一定的规则进行递增或递减,或者存在某种数值变化的模式。
-
观察特定区域的数值规律:有时候,二维数组中的特定区域可能存在一些数值规律。通过观察这些区域中元素的数值变化,可以发现其中的规律,并将其应用到其他区域。
-
利用数学公式或算法:对于一些特殊的二维数组,可能存在一些数学公式或算法来描述其中的规律。通过应用这些公式或算法,可以更容易地找到数据的规律。
下面是一些常见的二维数组数据找规律的示例:
最值相关:
- 找最大值和最小值:遍历整个二维数组,比较每个元素的大小,找出其中的最大值和最小值。
// 找到二维数组中的最大值和最小值 int max = array[0][0]; // 初始化最大值为数组第一个元素 int min = array[0][0]; // 初始化最小值为数组第一个元素// 遍历整个二维数组,比较每个元素的大小,更新最大值和最小值 for (int row = 0; row < array.length; row++) {for (int col = 0; col < array[row].length; col++) {if (array[row][col] > max) {max = array[row][col]; // 更新最大值}if (array[row][col] < min) {min = array[row][col]; // 更新最小值}} }// 输出最大值和最小值 System.out.println("最大值:" + max); System.out.println("最小值:" + min); - 判断是否存在特定的元素:遍历整个二维数组,通过比较元素的值,判断是否存在特定的元素。
// 判断二维数组中是否存在特定的元素 int targetElement = 5; // 要查找的目标元素 boolean elementExists = false; // 初始化是否存在目标元素的标志为false// 遍历整个二维数组,通过比较元素的值,判断是否存在目标元素 for (int row = 0; row < array.length; row++) {for (int col = 0; col < array[row].length; col++) {if (array[row][col] == targetElement) {elementExists = true; // 标记目标元素存在break; // 跳出内层循环}}if (elementExists) {break; // 跳出外层循环} }// 输出是否存在目标元素 System.out.println("是否存在元素 " + targetElement + ":" + elementExists);
和相关:
- 找每行的和:遍历二维数组的每一行,将该行的所有元素相加求和。
// 找到每行的和 for (int i = 0; i < array.length; i++) {int sum = 0;for (int j = 0; j < array[i].length; j++) {sum += array[i][j];}System.out.println("第 " + (i + 1) + " 行的和:" + sum); } - 找每列的和:遍历二维数组的每一列,将该列的所有元素相加求和。
// 找到每列的和 for (int j = 0; j < array[0].length; j++) {int sum = 0;for (int i = 0; i < array.length; i++) {sum += array[i][j];}System.out.println("第 " + (j + 1) + " 列的和:" + sum); } - 求行或列的和:遍历整个二维数组,将每行或者每列的元素进行累加求和。
// 求二维数组中指定行和指定列的和 int rowSum = 0; // 保存指定行的和 int colSum = 0; // 保存指定列的和 int targetRow = 2; // 指定行索引 int targetCol = 1; // 指定列索引// 遍历整个二维数组,累加指定行和指定列的元素 for (int i = 0; i < array.length; i++) {rowSum += array[targetRow][i]; colSum += array[i][targetCol]; }// 输出指定行和指定列的和 System.out.println("第 " + targetRow + " 行的和:" + rowSum); System.out.println("第 " + targetCol + " 列的和:" + colSum); - 找对角线的和:对角线分为主对角线和副对角线。主对角线从左上角到右下角,副对角线从右上角到左下角。分别求出对角线上的元素和。
// 找到对角线的和 int mainSum = 0; int antiSum = 0; for (int i = 0; i < array.length; i++) {mainSum += array[i][i];antiSum += array[i][array.length - 1 - i]; }System.out.println("主对角线的和:" + mainSum); System.out.println("副对角线的和:" + antiSum);
遍历相关:
- 螺旋顺序遍历:对于一个二维数组,按照顺时针螺旋的顺序遍历元素。我们可以使用四个变量来表示当前螺旋的上界、下界、左界、右界,然后按照顺时针方向不断缩小边界。
// 按顺时针螺旋顺序遍历二维数组元素 int top = 0; int bottom = array.length - 1; int left = 0; int right = array[0].length - 1;while (top <= bottom && left <= right) {// 从左到右for (int i = left; i <= right; i++) {System.out.println(array[top][i]);}top++;// 从上到下for (int i = top; i <= bottom; i++) {System.out.println(array[i][right]);}right--;// 从右到左if (top <= bottom) {for (int i = right; i >= left; i--) {System.out.println(array[bottom][i]);}bottom--;}// 从下到上if (left <= right) {for (int i = bottom; i >= top; i--) {System.out.println(array[i][left]);}left++;} } - 遍历特定条件的元素集合:对于一个二维数组,找出特定元素的集合。我们可以使用一个循环遍历数组,然后判断当前元素是否满足特定条件。
// 找出二维数组中特定元素的集合 List<Integer> resultList = new ArrayList<>(); int targetValue = 5; // 要查找的目标值for (int i = 0; i < array.length; i++) {for (int j = 0; j < array[i].length; j++) {if (array[i][j] == targetValue) {resultList.add(array[i][j]); // 将满足条件的元素添加到结果集合中}} }System.out.println(resultList); - 寻找对角线元素:对于一个正方形的二维数组,从左上角到右下角(或者从右上角到左下角)的对角线上的元素具有一些规律。
// 输出正方形二维数组的对角线元素 int n = array.length; // 假设是一个 n x n 的二维数组 // 输出左上角到右下角的对角线 for (int i = 0; i < n; i++) {System.out.println(array[i][i]); } // 输出右上角到左下角的对角线 for (int i = 0; i < n; i++) {System.out.println(array[i][n - 1 - i]); } - 寻找螺旋形元素:可以按照顺时针或者逆时针的方向,以螺旋状从外向内输出二维数组的元素。
// 按顺时针方向输出二维数组的元素 int m = array.length; // 行数 int n = array[0].length; // 列数 int rowStart = 0; int rowEnd = m - 1; int colStart = 0; int colEnd = n - 1;while (rowStart <= rowEnd && colStart <= colEnd) {// 输出上边界for (int i = colStart; i <= colEnd; i++) {System.out.println(array[rowStart][i]);}rowStart++;// 输出右边界for (int i = rowStart; i <= rowEnd; i++) {System.out.println(array[i][colEnd]);}colEnd--;// 输出下边界if (rowStart <= rowEnd) {for (int i = colEnd; i >= colStart; i--) {System.out.println(array[rowEnd][i]);}rowEnd--;}// 输出左边界if (colStart <= colEnd) {for (int i = rowEnd; i >= rowStart; i--) {System.out.println(array[i][colStart]);}colStart++;} } - 搜索特定元素的位置:可以使用遍历整个二维数组的方法来搜索特定元素的位置。
// 找到二维数组中特定值的位置(行和列索引) int targetValue = 5; // 要查找的目标值 int targetRowIndex = -1; // 初始化目标值的行索引为-1 int targetColIndex = -1; // 初始化目标值的列索引为-1// 遍历整个二维数组,找到目标值的位置 for (int row = 0; row < array.length; row++) {for (int col = 0; col < array[row].length; col++) {if (array[row][col] == targetValue) {targetRowIndex = row; // 更新目标值的行索引targetColIndex = col; // 更新目标值的列索引break; // 找到目标值后跳出内层循环}}if (targetRowIndex != -1 && targetColIndex != -1) {break; // 如果已找到目标值的位置,跳出外层循环} }// 输出目标值的位置 System.out.println("元素 " + targetValue + " 的位置:(" + targetRowIndex + ", " + targetColIndex + ")");
差值相关:
- 找相邻元素的差值:遍历二维数组,找到相邻元素之间的差值。
// 找到相邻元素的差值 for (int i = 0; i < array.length; i++) { // 遍历二维数组的行for (int j = 0; j < array[i].length - 1; j++) { // 遍历当前行的元素(除最后一个元素)int diff = array[i][j + 1] - array[i][j]; // 计算相邻两列元素的差值System.out.println("第 " + (i + 1) + " 行第 " + (j + 1) + " 列和第 " + (j + 2) + " 列的差值:" + diff); // 输出差值信息} }
元素翻转相关:
- 数组元素翻转:将二维数组的元素按指定规律进行翻转,例如将每一列的元素倒序排列。
// 对二维数组的每一行进行翻转(倒序排列) for (int i = 0; i < arr.length; i++) { // 遍历二维数组的行int start = 0; // 起始位置int end = arr[i].length - 1; // 结束位置while (start < end) { // 反转当前行的元素int temp = arr[i][start]; // 临时变量存储起始位置的值arr[i][start] = arr[i][end]; // 将结束位置的值赋给起始位置arr[i][end] = temp; // 将临时变量的值赋给结束位置start++; // 起始位置右移end--; // 结束位置左移} }
统计相关:
- 查找特定值的出现次数:统计二维数组中特定值的出现次数。
// 统计二维数组中特定值的出现次数 int target = 5; // 目标值 int count = 0; // 计数器,用于统计目标值出现的次数 for (int row = 0; row < arr.length; row++) { // 遍历二维数组的行for (int col = 0; col < arr[row].length; col++) { // 遍历二维数组的列if (arr[row][col] == target) { // 如果当前元素等于目标值count++; // 增加计数}} } System.out.println("元素 " + target + " 出现的次数:" + count); // 输出目标值出现的次数
3. 杨辉三角
杨辉三角,也称为帕斯卡三角形,是一个数学上的图形,它由数字构成的三角形。
杨辉三角的第一行只有一个数字 1,从第二行开始,每个数字都是它上方两个数字的和。具体来说,对于第n行第m个数字,它的值等于第n-1行第m-1个数字加上第n-1行第m个数字。
杨辉三角的特点是每个数字等于它上方两个数字之和,并且每一行的数字依次递增。它的结构非常规则,可以形成一个三角形的形状。
杨辉三角一些基本性质:
- 第n行有n个元素。
- 第n行的元素可以通过组合数公式计算得到,第n行的第k个元素(从0开始)等于C(n, k),其中C(n, k)表示从n个元素中选择k个元素的组合数。
- 杨辉三角中的每一行都是对称的。
可以利用二维数组的行与列的关系来实现杨辉三角:
public class YanghuiTriangle {public static void main(String[] args) {int numRows = 5; // 杨辉三角的行数int[][] yanghuiTriangle = new int[numRows][]; // 用于存储三角形的二维数组// 填充杨辉三角的值for (int row = 0; row < numRows; row++) {yanghuiTriangle[row] = new int[row + 1];yanghuiTriangle[row][0] = 1; // 每行的第一个元素为1yanghuiTriangle[row][row] = 1; // 每行的最后一个元素为1// 计算每行其余元素的值for (int col = 1; col < row; col++) {// 当前行和列的元素值等于上一行同列元素和上一行同列前一个元素的和yanghuiTriangle[row][col] = yanghuiTriangle[row-1][col-1] + yanghuiTriangle[row-1][col];}}// 输出杨辉三角for (int i = 0; i < yanghuiTriangle.length; i++) {for (int j = 0; j < yanghuiTriangle[i].length; j++) {System.out.print(yanghuiTriangle[i][j] + " ");}System.out.println();}}
}
以上代码输出的结果为:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1 相关文章:

蓝桥杯备考随手记: 常见的二维数组问题
在Java中,二维数组是一种可以存储多个元素的数据结构。它由多个一维数组组成,这些一维数组可以看作是行和列的组合,形成了一个矩阵。 1. 二维数组旋转问题 二维数组的旋转是指将数组中的元素按照一定规则进行旋转。通常有两种常见的旋转方式…...

Java | Leetcode Java题解之第28题找出字符串中第一个匹配项的下标
题目: 题解: class Solution {public int strStr(String haystack, String needle) {int n haystack.length(), m needle.length();if (m 0) {return 0;}int[] pi new int[m];for (int i 1, j 0; i < m; i) {while (j > 0 && needl…...
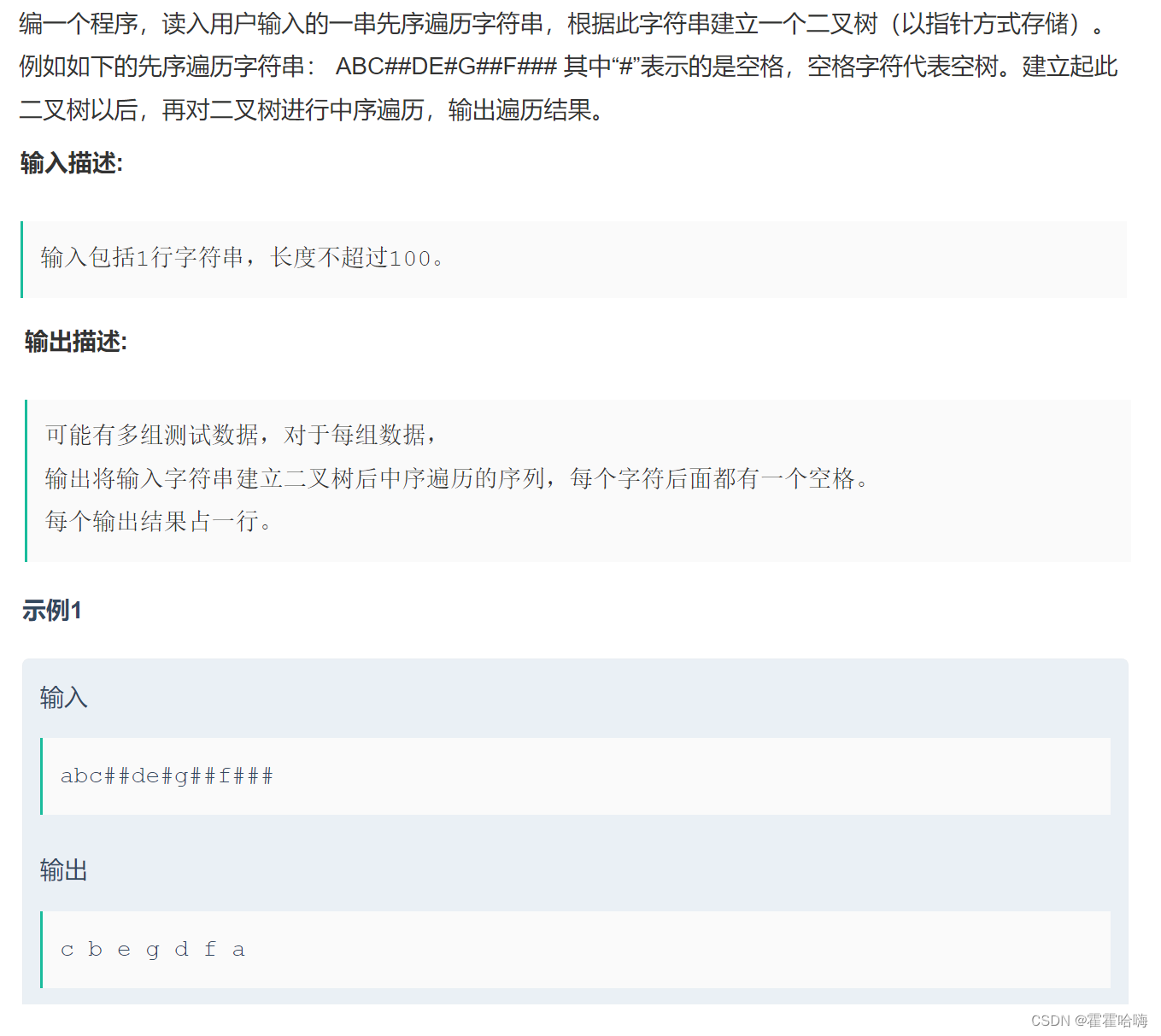
【数据结构与算法】:二叉树经典OJ
目录 1. 二叉树的前序遍历 (中,后序类似)2. 二叉树的最大深度3. 平衡二叉树4. 二叉树遍历 1. 二叉树的前序遍历 (中,后序类似) 这道题的意思是对二叉树进行前序遍历,把每个结点的值都存入一个数组中,并且返回这个数组。 思路&…...

uniapp——长按识别二维码
说明 转变思路,长按图片,进入预览图片,这时候再长按就可以了。 <view class"codeMain"><view class"codeWhite" longpress"handleLongPress(i.image(qrcode))"><image :src"i.image(qrc…...
云服务器环境web环境搭建之JDK、redis、mysql
一、Linux安装jdk,手动配置环境 链接: https://pan.baidu.com/s/1LRgRC5ih7B9fkc588uEQ1whttps://pan.baidu.com/s/1LRgRC5ih7B9fkc588uEQ1w 提取码: 0413 tar -xvf 压缩包名 修改配置文件/etc/profile 二、安装redis环境 方案一: Linux下安装配置r…...

第1章 计算机网络体系结构
王道学习 【考纲内容】 (一)计算机网络概述 计算机网络的概念、组成与功能;计算机网络的分类; 计算机网络的性能指标 (二)计算机网络体系结构与参考模型 计算机网络分层结…...
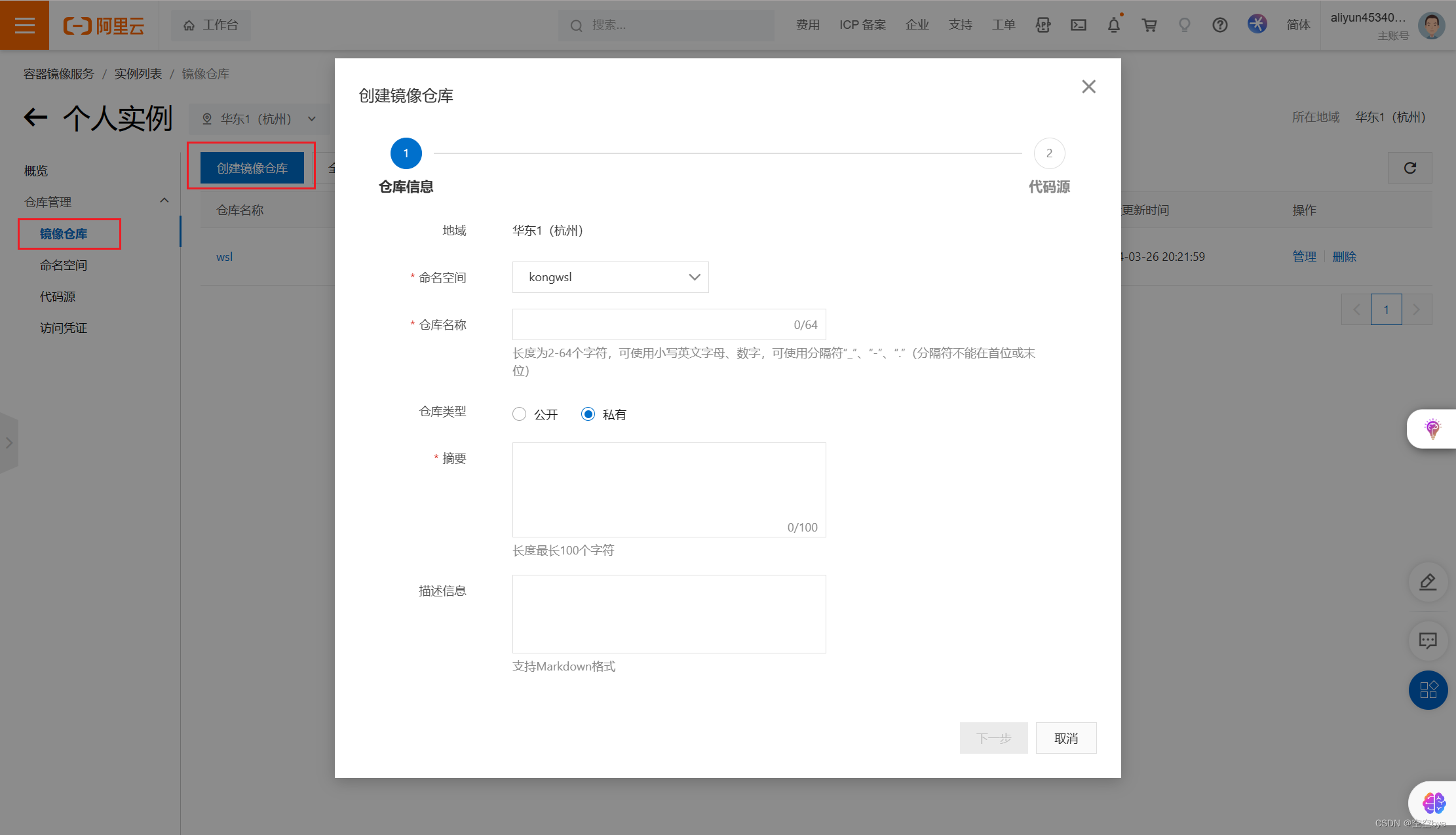
Docker之自定义镜像上传至阿里云
一、Alpine介绍 Alpine Linux是一个轻量级的Linux发行版,专注于安全、简单和高效。它采用了一个小巧的内核和基于musl libc的C库,使得它具有出色的性能和资源利用率。 Alpine Linux的主要特点包括: 小巧轻量:Alpine Linux的安装…...
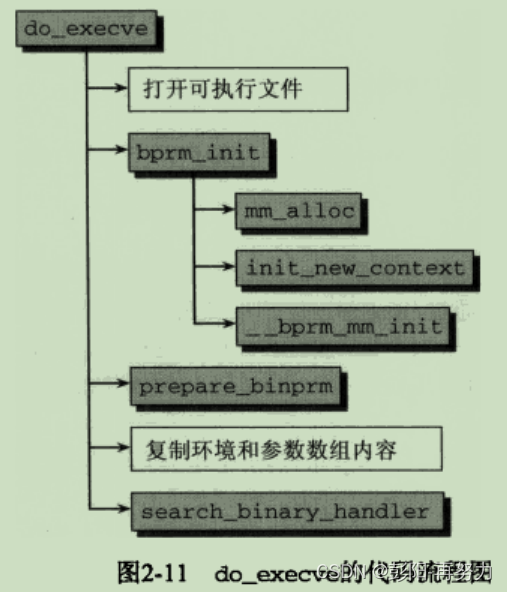
《深入Linux内核架构》第2章 进程管理和调度 (2)
目录 2.4 进程管理相关的系统调用 2.4.1 进程复制 2.4.2 内核线程 2.4.3 启动新程序 2.4.4 退出进程 本专栏文章将有70篇左右,欢迎关注,订阅后续文章。 2.4 进程管理相关的系统调用 2.4.1 进程复制 1. _do_fork函数 fork vfork clone都最终调用_…...
PostgreSQL的psql命令)
(四)PostgreSQL的psql命令
PostgreSQL的psql命令 基础信息 OS版本:Red Hat Enterprise Linux Server release 7.9 (Maipo) DB版本:16.2 pg软件目录:/home/pg16/soft pg数据目录:/home/pg16/data 端口:5777psql 是 PostgreSQL 数据库的命令行界面…...

前端使用minio传输文件
minio官方文档 minio-js可以支持ts。 安装完可能会出现 Can‘t import the named export ‘xxx‘ from non EcmaScript module (only default export is available)可以尝试降低minio的版本 npm install minio7.0.18 --save代码: 初始化 const Minio require(…...

[大模型] BlueLM-7B-Chat WebDemo 部署
BlueLM-7B-Chat WebDemo 部署 模型介绍 BlueLM-7B 是由 vivo AI 全球研究院自主研发的大规模预训练语言模型,参数规模为 70 亿。BlueLM-7B 在 C-Eval 和 CMMLU 上均取得领先结果,对比同尺寸开源模型中具有较强的竞争力(截止11月1号)。本次发布共包含 7…...

一文了解ERC404协议
一、ERC404基础讲解 1、什么是ERC404协议 ERC404协议是一种实验性的、混合的ERC20/ERC721实现的,具有原生流动性和碎片化的协议。即该协议可让NFT像代币一样进行拆分交易。是一个图币的互换协议。具有原生流动性和碎片化的协议。 这意味着通过 ERC404 协议…...

iOS cocoapods pod FrozenError and RuntimeError
0x00 报错日志 /Library/Ruby/Gems/2.6.0/gems/cocoapods-1.12.0/lib/cocoapods/user_interface/error_report.rb:34:in force_encoding: cant modify frozen String (FrozenError)from /Library/Ruby/Gems/2.6.0/gems/cocoapods-1.12.0/lib/cocoapods/user_interface/error_r…...
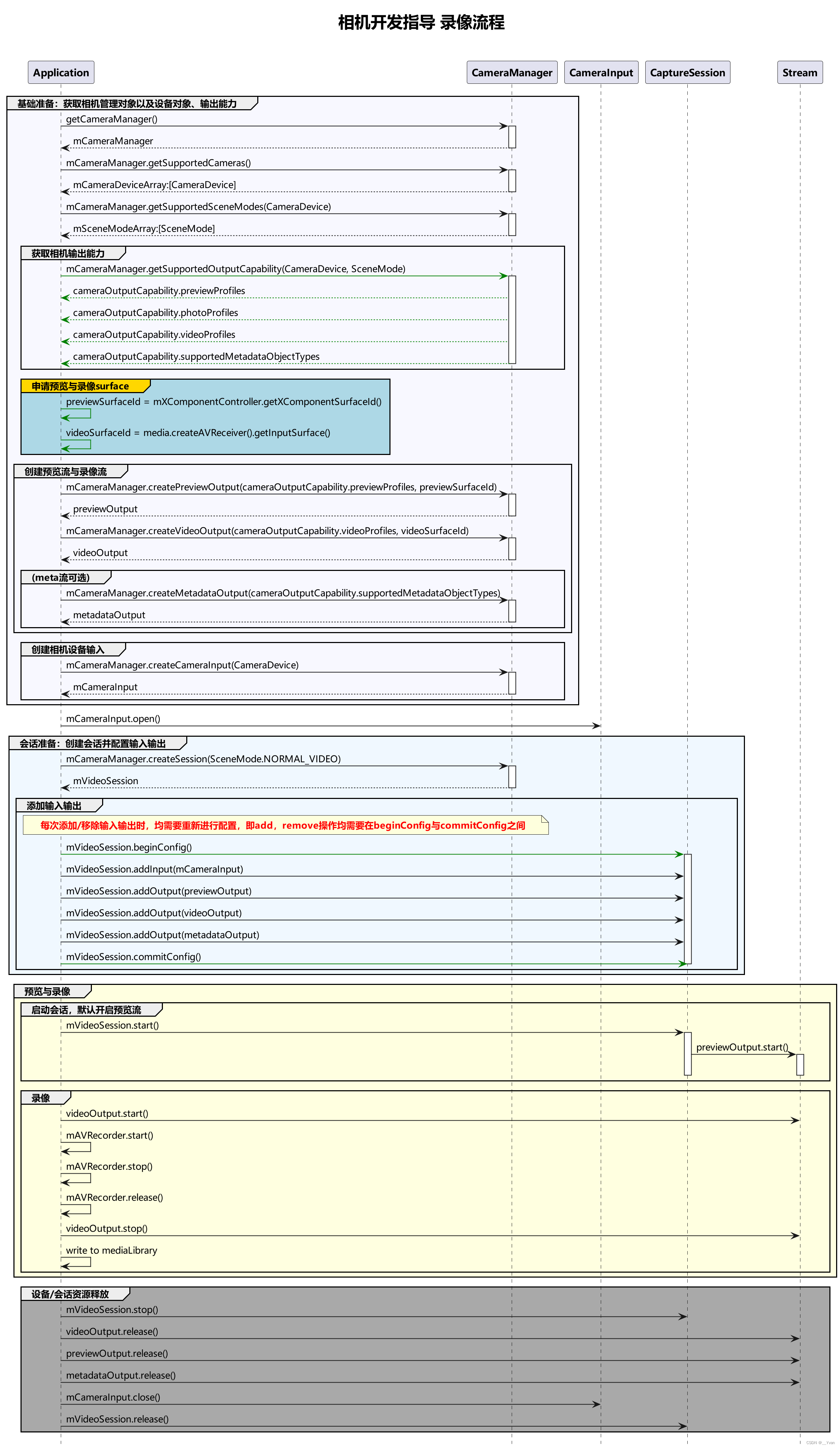
【鸿蒙开发】第二十章 Camera相机服务
1 简介 开发者通过调用Camera Kit(相机服务)提供的接口可以开发相机应用,应用通过访问和操作相机硬件,实现基础操作,如预览、拍照和录像;还可以通过接口组合完成更多操作,如控制闪光灯和曝光时间、对焦或调焦等。 2 …...

JS阅读笔记
myweb3.html <video id"video" width"400" height"300" autoplay></video> <button id"capture-btn">拍摄图片</button> <canvas id"canvas" width"400" height"300">&…...

基于spring boot的留守儿童爱心管理系统
基于spring boot的留守儿童爱心管理系统设计与实现 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开…...

python输入某年某月某日判断这一天是这一年的第几天
如何使用python实现输入某年某月某日判断这一天是这一年的第几天 from datetime import datetime #引入日期类 def is_leap_year(year):"""判断是否为闰年"""return (year % 4 0 and year % 100 ! 0) or (year % 400 0)# 根据年份和月份返回当…...
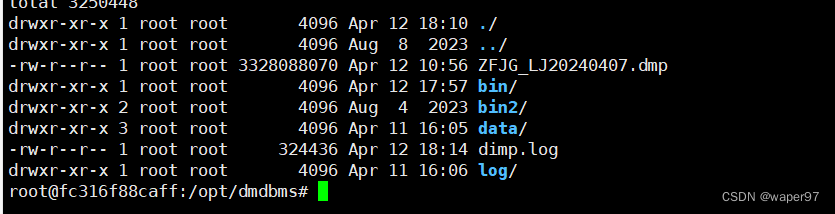
docker 上达梦导入dump文件报错:本地编码:PG GBK,导入女件编码:PGGB18030
解决方案: 第一步进入达梦数据容器内部 docker exec -it fc316f88caff /bin/bash 第二步:在容器中 /opt/dmdbms/bin目录下 执行命令 cd /opt/dmdbms/bin./dimp USERIDSYSDBA/SYSDBA001 FILE/opt/dmdbms/ZFJG_LJ20240407.dmp SCHEMASZFJG_LJUSERIDSYSD…...
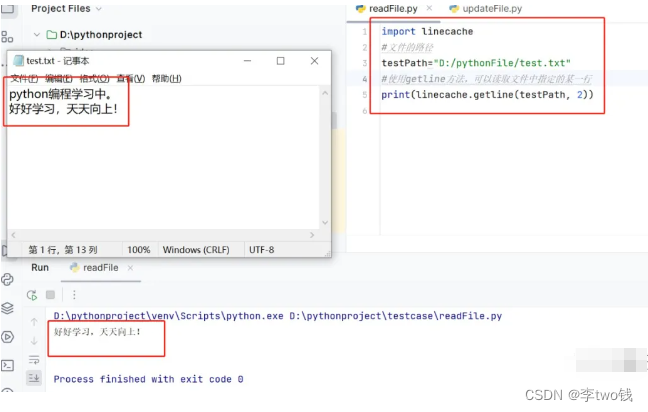
一起学习python——基础篇(19)
今天来说一下python的如何修改文件名称、获取文件大小、读取文中指定的某一行内容。 1、修改文件名称: import os testPath"D:/pythonFile/test.txt" testPath2"D:/pythonFile/test2.txt" #修改文件名称使用rename方法, #第一个参…...
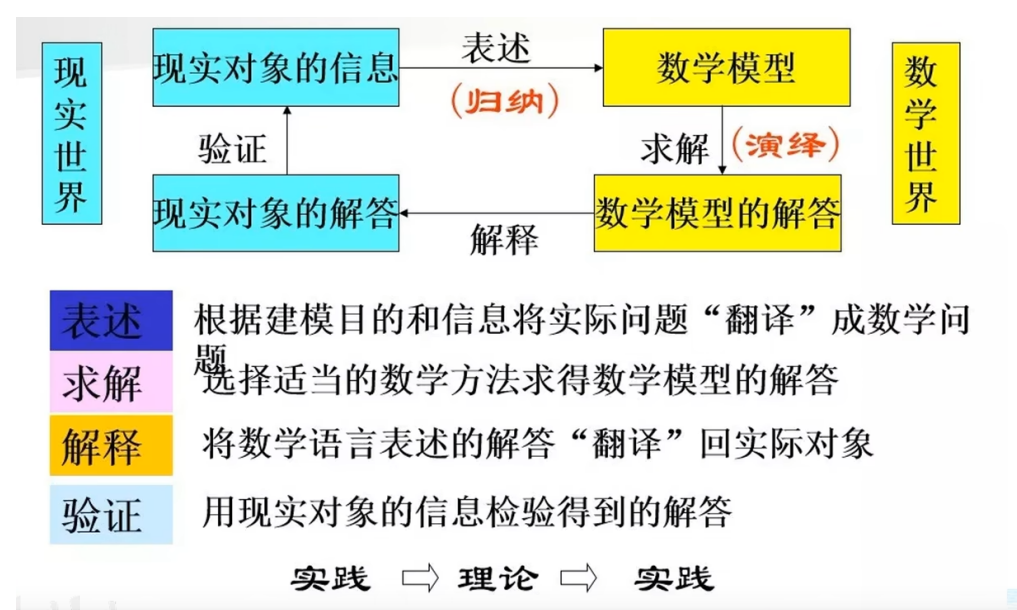
数模 初见数建
文章目录 初见数学建模1.1 数学建模是什么1.2 数学建模的概述1.3 如何学习数学建模---分模块化1.4 数学建模前提了解1.5 数学建模的六个步骤1.6 如何备战建模比赛1.7 数学建模赛题类型1.8 数学建模算法体系概述 初见数学建模 1.1 数学建模是什么 1.原型与模型 原型ÿ…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
