【机器学习】一文掌握机器学习十大分类算法(上)。
十大分类算法
- 1、引言
- 2、分类算法总结
- 2.1 逻辑回归
- 2.1.1 核心原理
- 2.1.2 算法公式
- 2.1.3 代码实例
- 2.2 决策树
- 2.2.1 核心原理
- 2.2. 代码实例
- 2.3 随机森林
- 2.3.1 核心原理
- 2.3.2 代码实例
- 2.4 支持向量机
- 2.4.1 核心原理
- 2.4.2 算法公式
- 2.4.3 代码实例
- 2.5 朴素贝叶斯
- 2.5.1 核心原理
- 2.5.2 算法公式
- 2.5.3 代码实例
- 3、总结
1、引言
小屌丝:鱼哥,分类算法都有哪些?
小鱼:也就那几种了
小屌丝:哪几种啊?
小鱼:逻辑归回、决策树、随机森林、支持向量机…你问这个干嘛
小屌丝:我想捋一捋,哪些是分类算法
小鱼:我在【机器学习&深度学习】专栏已经写过了啊
小屌丝:那不是一篇只能学习一个技能嘛
小鱼:那你想咋的?
小屌丝:我想一篇学习多个技能。
小鱼:我… 的乖乖, 你真是个…~~

小屌丝: 别这么夸,我会不好意思的
小鱼:… 算了,我还是整理一下思路,写文章吧
小屌丝:可以可以。
2、分类算法总结
2.1 逻辑回归
2.1.1 核心原理
逻辑回归是用于二分类问题的统计方法,它通过将数据输入的线性组合通过逻辑函数(通常是Sigmoid函数)映射到0和1之间,从而预测概率。
2.1.2 算法公式
逻辑回归的核心公式为 P ( Y = 1 ) = 1 1 + e − ( β 0 + β 1 X 1 + . . . + β n X n ) P(Y=1) = \frac{1}{1 + e^{-(\beta_0 + \beta_1X_1 + ... + \beta_nX_n)}} P(Y=1)=1+e−(β0+β1X1+...+βnXn)1,
其中 P ( Y = 1 ) P(Y=1) P(Y=1)是给定X时Y=1的概率。
敲黑板:
详细内容可以参照小鱼的专篇:
- 《【机器学习】有监督学习算法之:逻辑回归》
- 《【机器学习】一文掌握逻辑回归全部核心点(上)。》
- 《【机器学习】一文掌握逻辑回归全部核心点(下)。》
2.1.3 代码实例
代码实例
# -*- coding:utf-8 -*-
# @Time : 2024-04-03
# @Author : Carl_DJfrom sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 创建逻辑回归模型并训练
model = LogisticRegression(max_iter=200)
model.fit(X_train, y_train)# 进行预测
predictions = model.predict(X_test)
print(predictions)
2.2 决策树
2.2.1 核心原理
决策树通过递归地选择最优特征,并根据该特征的不同取值对数据进行分割,每个分割为一个树的分支,直到满足停止条件。
敲黑板:
详细内容可以参照小鱼的专篇:
- 《【机器学习】监督学习算法之:决策树》
2.2. 代码实例
代码实例
# -*- coding:utf-8 -*-
# @Time : 2024-04-03
# @Author : Carl_DJfrom sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 创建决策树模型并训练
model = DecisionTreeClassifier()
model.fit(X_train, y_train)# 进行预测
predictions = model.predict(X_test)
print(predictions)
2.3 随机森林
2.3.1 核心原理
随机森林是一种集成学习方法,它构建多个决策树并将它们的预测结果进行投票或平均,以提高预测的准确性和稳定性。
敲黑板:
详细内容可以参照小鱼的专篇:
- 《【机器学习】必会算法之:随机森林》
2.3.2 代码实例
代码实例
# -*- coding:utf-8 -*-
# @Time : 2024-04-03
# @Author : Carl_DJfrom sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 创建随机森林模型并训练
model = RandomForestClassifier()
model.fit(X_train, y_train)# 进行预测
predictions = model.predict(X_test)
print(predictions)
2.4 支持向量机
2.4.1 核心原理
SVM通过找到一个超平面来最大化不同类别之间的边界距离,以达到分类目的。
对于线性不可分的数据,SVM使用核技巧映射到更高维度空间中实现分离。
敲黑板:
详细内容可以参照小鱼的专篇:
- 《【机器学习】有监督学习算法之:支持向量机》
2.4.2 算法公式
SVM的目标是最小化 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i ||w||^2 + C\sum_{i=1}^{n}\xi_i ∣∣w∣∣2+C∑i=1nξi,其中C是正则化参数, ξ i \xi_i ξi是松弛变量。
2.4.3 代码实例
代码实例
# -*- coding:utf-8 -*-
# @Time : 2024-04-03
# @Author : Carl_DJfrom sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 创建SVM模型并训练
model = SVC()
model.fit(X_train, y_train)# 进行预测
predictions = model.predict(X_test)
print(predictions)
2.5 朴素贝叶斯
2.5.1 核心原理
朴素贝叶斯基于贝叶斯定理,假设特征之间相互独立。
它通过计算给定特征下每个类别的条件概率来进行分类。
2.5.2 算法公式
P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) P ( X ) P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)P(Y),其中 P ( Y ∣ X ) P(Y|X) P(Y∣X)是给定特征X下类别Y的条件概率。
2.5.3 代码实例
# -*- coding:utf-8 -*-
# @Time : 2024-01-21
# @Author : Carl_DJfrom sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 创建朴素贝叶斯模型并训练
model = GaussianNB()
model.fit(X_train, y_train)# 进行预测
predictions = model.predict(X_test)
print(predictions)
3、总结
以上介绍的五种机器学习分类算法各有特点和应用场景,如:
- 逻辑回归和朴素贝叶斯适用于小规模数据集,
- 决策树和随机森林适用于处理复杂的非线性关系,
- SVM适用于高维数据的分类问题。
选择合适的算法取决于具体问题、数据集的特性以及预期的性能要求。
掌握这些算法的原理和使用方法,可以有效提升机器学习项目的开发效率和效果。
敲黑板:
另一篇,则点击文字即可到达:《【机器学习】一文掌握机器学习十大分类算法(下)。》
我是小鱼:
- CSDN 博客专家;
- 阿里云 专家博主;
- 51CTO博客专家;
- 企业认证金牌面试官;
- 多个名企认证&特邀讲师等;
- 名企签约职场面试培训、职场规划师;
- 多个国内主流技术社区的认证专家博主;
- 多款主流产品(阿里云等)测评一、二等奖获得者;
关注小鱼,学习【机器学习】&【深度学习】领域的知识。
相关文章:

【机器学习】一文掌握机器学习十大分类算法(上)。
十大分类算法 1、引言2、分类算法总结2.1 逻辑回归2.1.1 核心原理2.1.2 算法公式2.1.3 代码实例 2.2 决策树2.2.1 核心原理2.2. 代码实例 2.3 随机森林2.3.1 核心原理2.3.2 代码实例 2.4 支持向量机2.4.1 核心原理2.4.2 算法公式2.4.3 代码实例 2.5 朴素贝叶斯2.5.1 核心原理2.…...

策略模式(知识点)——设计模式学习笔记
文章目录 0 概念1 使用场景2 优缺点2.1 优点2.2 缺点 3 实现方式4 和其他模式的区别5 具体例子实现5.1 实现代码 0 概念 定义:定义一个算法族,并分别封装起来。策略让算法的变化独立于它的客户(这样就可在不修改上下文代码或其他策略的情况下…...

Python学习从0开始——专栏汇总
Python学习从0开始——000参考 一、推荐二、基础三、项目一 一、推荐 Hello World in Python - 这个项目列出了用Python实现的各种"Hello World"程序。 Python Tricks - 这个项目包含了Python中的高级技巧和技术。 Think Python - 这是一本教授Python的在线书籍&…...

【iOS ARKit】Web 网页中嵌入 AR Quick Look
在支持 ARKit 的设备上,iOS 12 及以上版本系统中的 Safari浏览器支持 AR Quick Look, 因此可以通过浏览器直接使用3D/AR 的方式展示 Web 页面中的模型文件,目前 Web 版本的AR Quick Look 支持USDZ 格式文件。苹果公司有一个自建的3D模型示例库…...
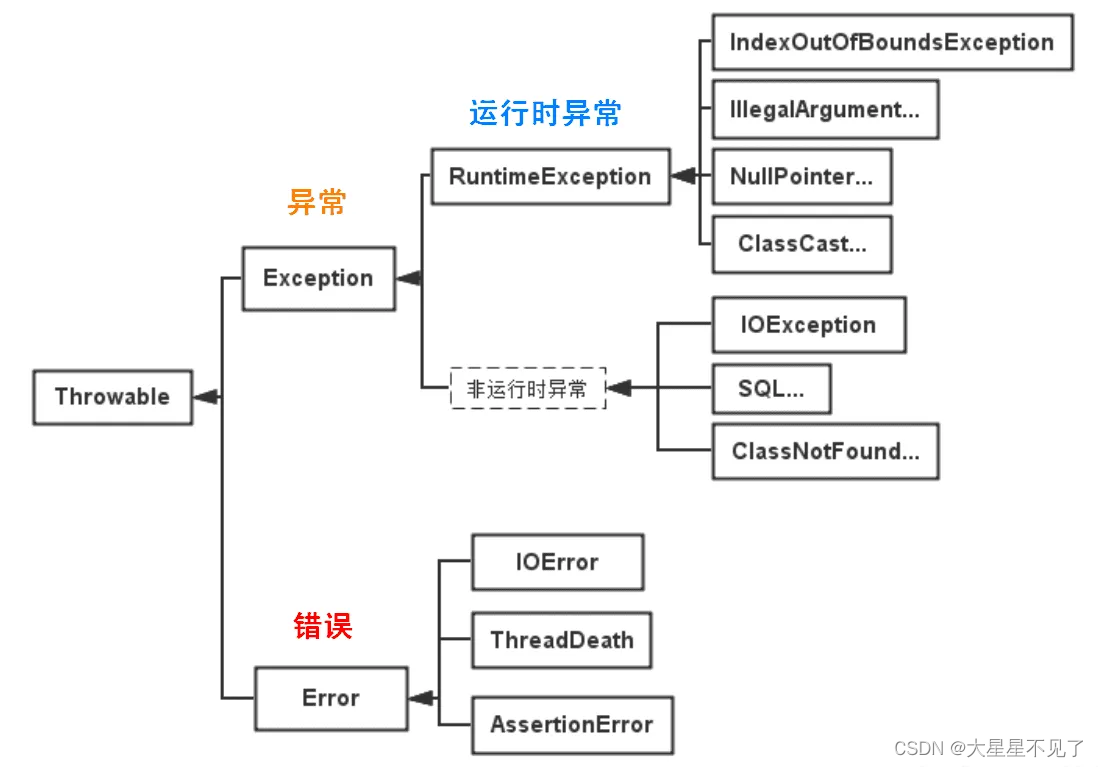
Java基础-知识点03(面试|学习)
Java基础-知识点03 String类String类的作用及特性String不可以改变的原因及好处String、StringBuilder、StringBuffer的区别String中的replace和replaceAll的区别字符串拼接使用还是使用StringbuilderString中的equal()与Object方法中equals()区别String a new String("a…...

【GIS学习笔记】ArcGIS/QGIS如何修改字段名称、调整字段顺序?
在先前的ArcGIS学习中,了解到字段名称是不能修改的,只能用新建一个字段赋值过去再删除原字段这种方法实现,字段顺序的调整如果通过拖拽也是不能持久的,需要用导出一个新数据这种方法进行保存,可参考以下链接࿱…...

Study Pyhton
PyCharm PyCharm是一个写python代码的软件,用PyCharm写代码比较方便。 PyCharm快捷键ctrl alt s打开软件设置ctrl d复制当前行代码 shift alt 上\下将当前行代码上移或下移crtl shift f10运行当前代码文件shiftf6重命名文件 ctrl a全选ctrl c\v\x复制、粘贴、…...

【MySQL】:深入解析多表查询(下)
🎥 屿小夏 : 个人主页 🔥个人专栏 : MySQL从入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一. 自连接1.1 自连接查询1.2 联合查询 二. 子查询2.1 概述2.2 分类2.3 标量子查…...

图像入门处理4(How to get the scaling ratio between different kinds of images)
just prepare for images fusion and registration ! attachments for some people who need link1 图像处理入门 3...

【项目精讲】Swagger接口文档以及使用方式
Swagger 介绍 Swagger 是一个规范和完整的框架,用于生成、描述、调用和可视化 RESTful 风格的 Web 服务(https://swagger.io/) 前后端分离开发,有利于团队合作接口的文档在线自动生成,降低后端开发人员编写接口文档的负担功能测试 如何使…...
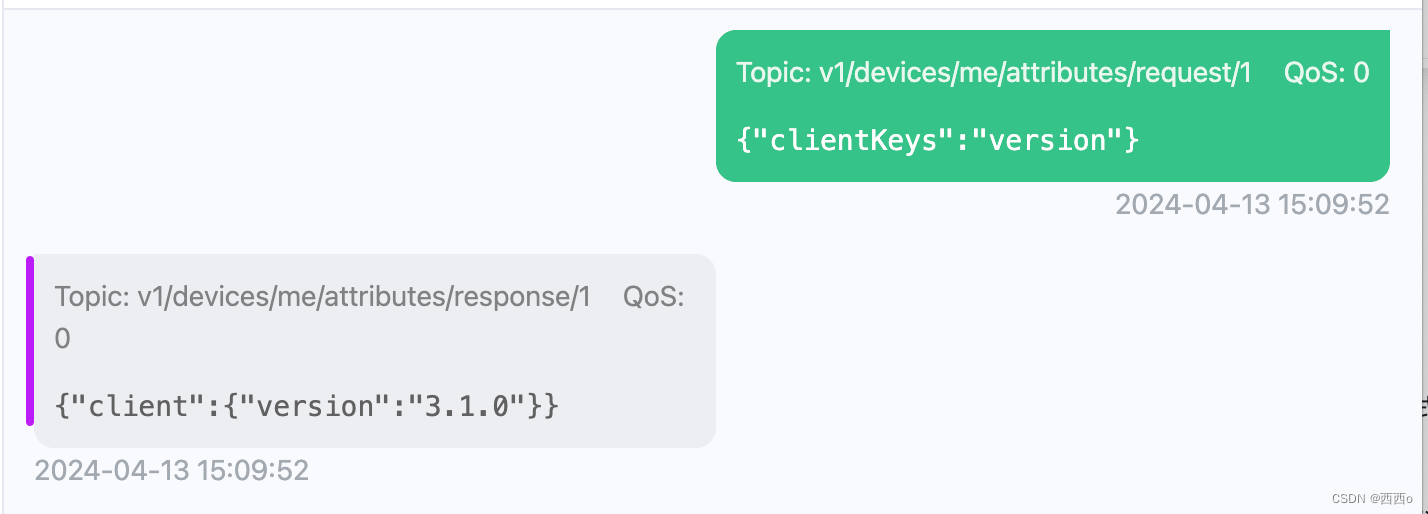
ThingsBoard通过服务端获取客户端属性或者共享属性
MQTT基础 客户端 MQTT连接 通过服务端获取属性值 案例 1、首先需要创建整个设备的信息,并复制访问令牌 2、通过工具MQTTX连接上对应的Topic 3、测试链接是否成功 4、通过服务端获取属性值 5、在客户端查看对应的客户端属性或者共享属性的key 6、查看整个…...
删除有序数组中的重复项(79)排序矩阵查找)
(78)删除有序数组中的重复项(79)排序矩阵查找
文章目录 1. 每日一言2. 题目(78)删除有序数组中的重复项2.1 解题思路2.2 代码 3. 题目(79)排序矩阵查找3.1 解题思路3.1.1 暴力查找暴力查找代码 3.1.2 二分查找二分查找代码 3.1.3 贪心贪心代码 4. 结语 1. 每日一言 水晶帘动微风起,满架蔷薇一院香。 —高骈- 2.…...
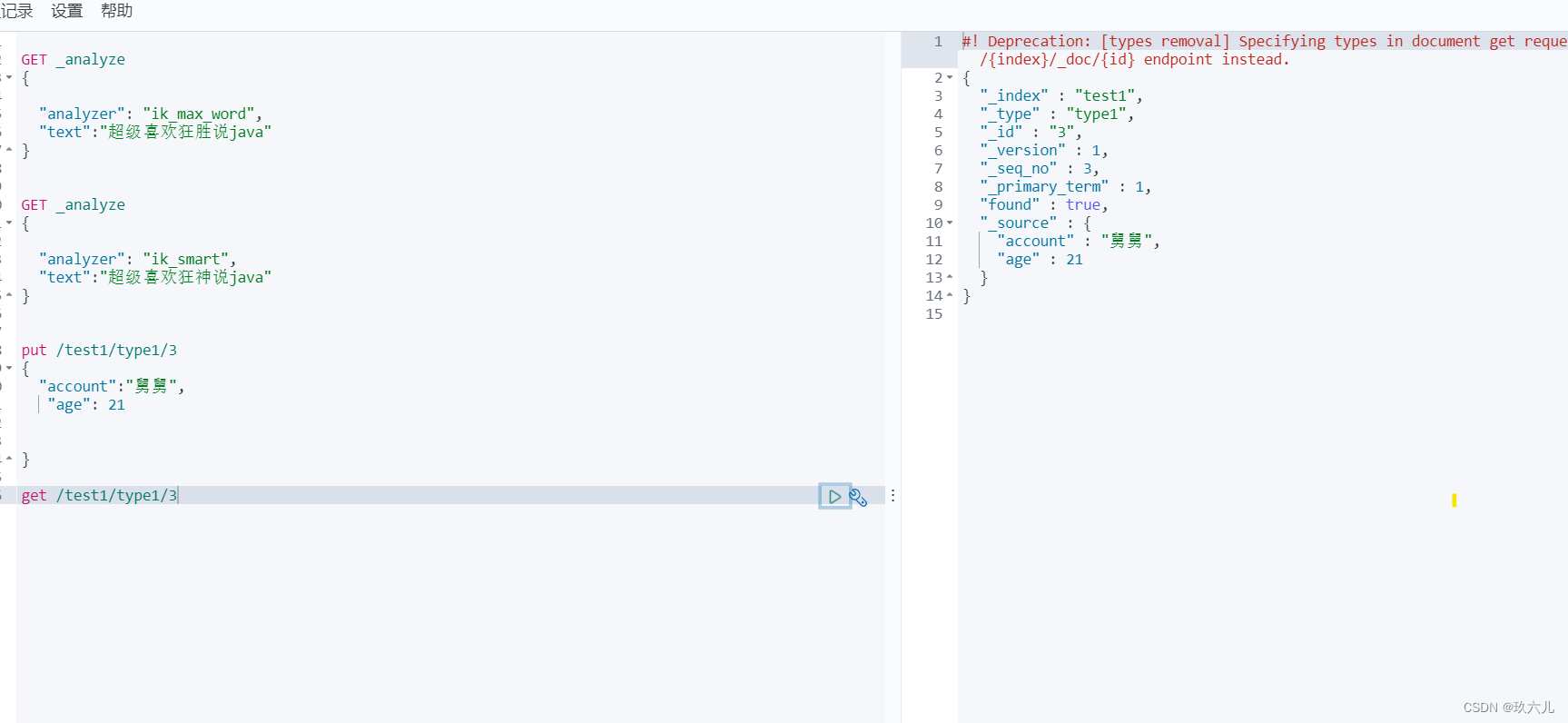
elasticSearch从零整合springboot项目实操
type会被弃用 ,就是说之后的elasticSearch中只会存在 索引(indices) 和 一行(document) 和字段(fields) elasticSearch 和solr的区别最大的就是 es对应的 是 json的格式 。 solr有xml和josn等…...

【Linux实践室】Linux高级用户管理实战指南:用户所属组变更操作详解
🌈个人主页:聆风吟_ 🔥系列专栏:Linux实践室、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. ⛳️任务描述二. ⛳️相关知识2.1 🔔Linux查看用户所属组2.1.1 👻使…...

C语言: 字符串函数(下)
片头 在上一篇中,我们介绍了字符串函数。在这一篇章中,我们将继续学习字符串函数,准备好了吗?开始咯! 1.strncpy函数 1.1 strncpy函数的用法 strncpy是C语言中的一个字符串处理函数,它用于将一个字符串的一部分内容…...

WPF 数据绑定类属性 和数据更新
WPF中数据绑定是一个非常强大的功能,不仅可以绑定后台数据,还可以进行实时更新。 数据绑定实例 : 在后台创建模型类,然后在标签页面进行导入并绑定。 第一步: // 在后台创建模型类 public class MyData {public string Name { get; set; }…...
使用云服务器搭建CentOS操作系统
云服务器搭建CentOS操作系统 前言一、购买云服务器腾讯云阿里云华为云 二、使用 XShell 远程登陆到 Linux关于 Linux 桌面下载 XShell安装XShell查看 Linux 主机 ip使用 XShell 登陆主机 三、无法使用密码登陆的解决办法 前言 CentOS是一种基于Red Hat Enterprise Linux&#…...

unity的引用传递和数组的联系
引用传递 //引用传递 static void SetY(out int x,out int y ){x 0;y 0;x 1000;}static void Main(string[] args){int x 0;int y 10;SetY(out x, out y);Console.WriteLine($"x{x},y{y}");} 结果是:x1000,y0 数组的引用传递 数组值…...

Android bug Unresolved reference: BR
新建项目后 导入viewBinding 编译后提示 Unresolved reference: BR 解决办法 app 目录下 build.gradle 中 plugins 节点 添加 id kotlin-kapt参考 https://stackoverflow.com/questions/77409050/could-not-find-androidx-corecore-ktx1-8-10...
 ECS机制与概述)
Unity DOTS1.0 入门(1) ECS机制与概述
ECS机制与概述 Entity:实体 由一个一个的Component组合在一起,是连续的内存布局。通过EnitityManager来负责高效的分配和释放相关entity. World:世界 一个entity的集合,在当前世界里面,每个Entity都有唯一不同的entityld;运行时Unity会自动创建一个D…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
