代码随想录 二叉树—二叉搜索树中的搜索
思路:当节点为空或者等于目标值,直接返回。由于是二叉搜索树,特点是左子树的值都小于根节点值,右子树的值均大于根节点,那么,左右子树的构建可以通过值的判断来递归调用。
c++题解:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if(root==NULL||root->val==val) return root;TreeNode* result=NULL;if(root->val>val) result=searchBST(root->left,val);if(root->val<val) result=searchBST(root->right,val);return result;}
};相关文章:

代码随想录 二叉树—二叉搜索树中的搜索
思路:当节点为空或者等于目标值,直接返回。由于是二叉搜索树,特点是左子树的值都小于根节点值,右子树的值均大于根节点,那么,左右子树的构建可以通过值的判断来递归调用。 c题解: /*** Defini…...
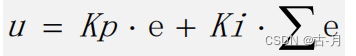
⑤-1 学习PID--什么是PID
PID 算法可以用于温度控制、水位控制、飞行姿态控制等领域。后面我们通过PID 控制电机进行说明。 自动控制系统 在直流有刷电机的基础驱动中,如果电机负载不变,我们只要设置固定的占空比(电压),电机的速度就会稳定在…...
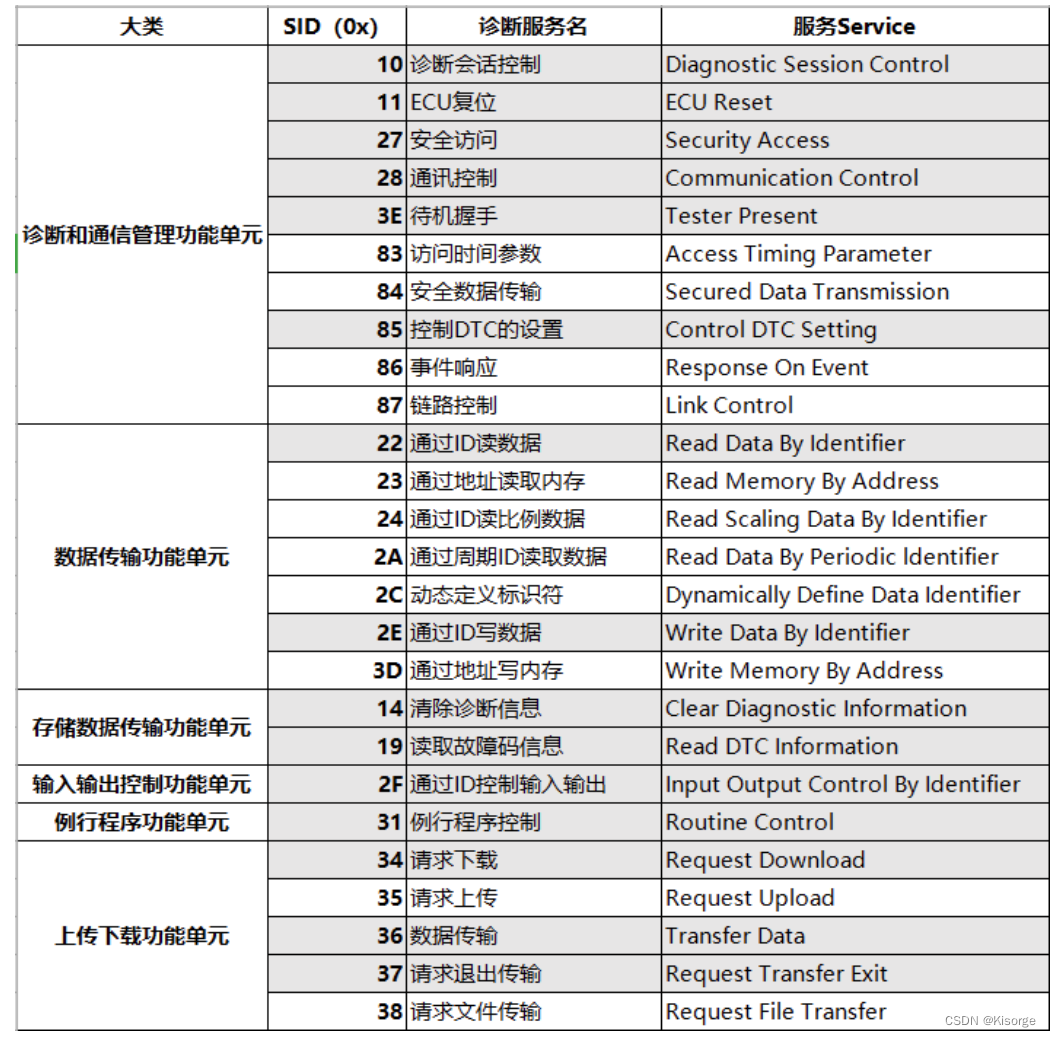
【OTA】STM32-OTA升级——持续更新
【OTA】STM32-OTA升级——持续更新 文章目录 前言一、ymodem串口协议1、Ymodem 协议2、PC3、蓝牙4、WIFI云平台 二、UDS车载协议1.UDS协议 总结 前言 提示:以下是本篇文章正文内容,下面案例可供参考 一、ymodem串口协议 1、Ymodem 协议 STM32 Ymodem …...
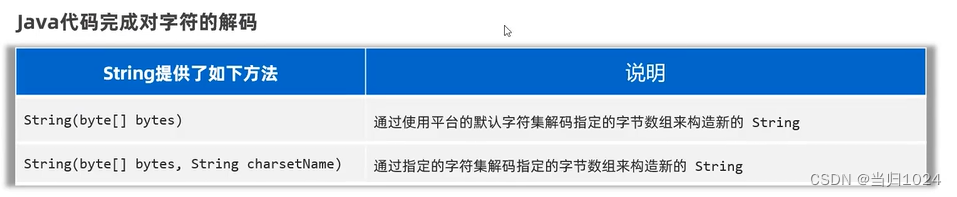
java 字符集
ASCII 与 GBK ASCII:英文专用GBK:中文专用 万国码 unicode想要统一这个世界上所有的语言,所以创造了UTF-32但是使用32位,也就是4个字节,对于很多语言来说,过于奢侈,也会造成通信效率和存储效率变低 UTF-8 unicode 创造…...

Alibaba --- 如何写好 Prompt ?
如何写好 Prompt 提示工程(Prompt Engineering)是一项通过优化提示词(Prompt)和生成策略,从而获得更好的模型返回结果的工程技术。总体而言,其实现逻辑如下: (注:示例图…...
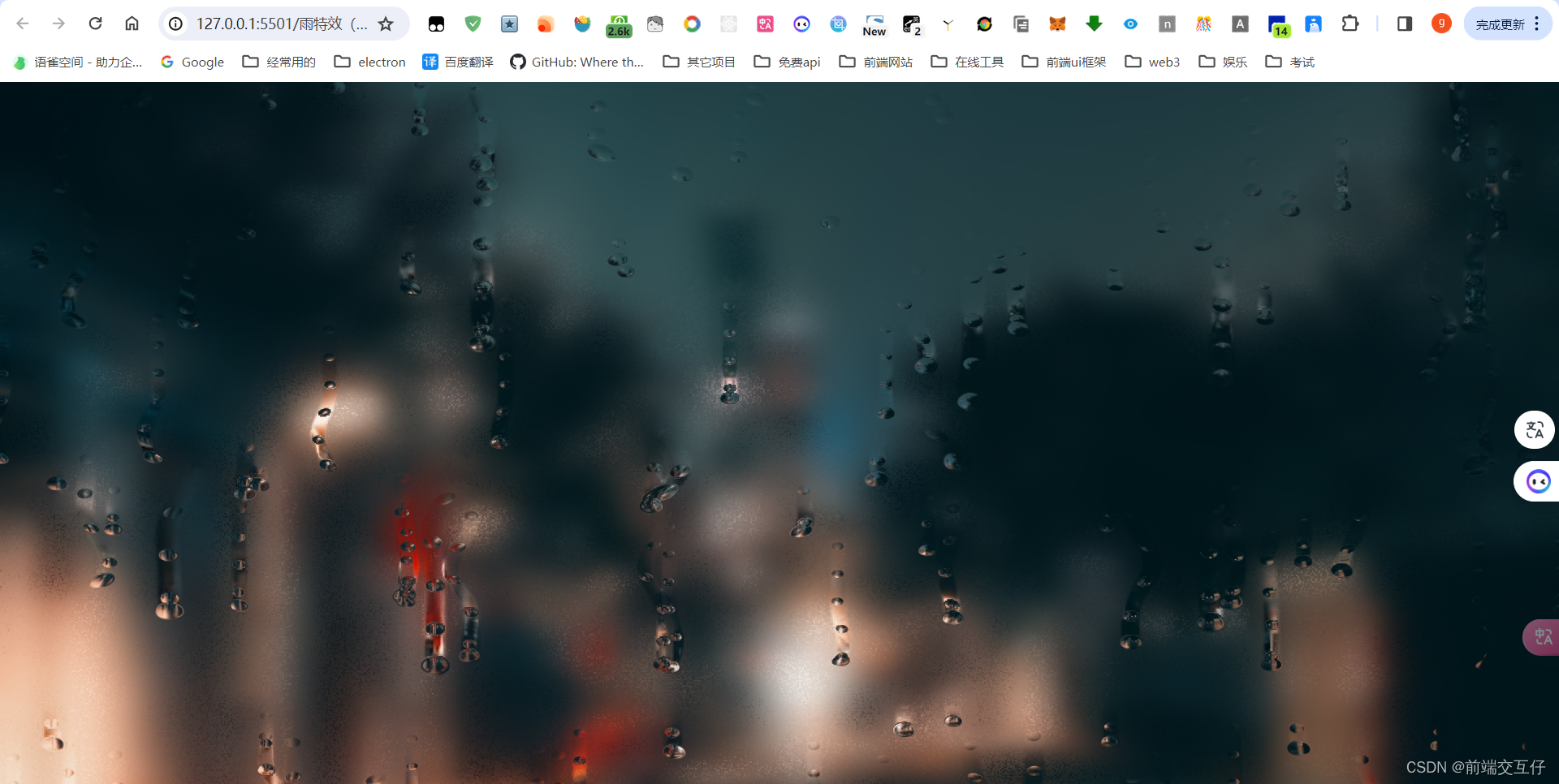
用html写一个雨的特效
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>雨特效</title><link rel"stylesheet" href"./style.css"> </head> <body> <div id"wrap-textu…...
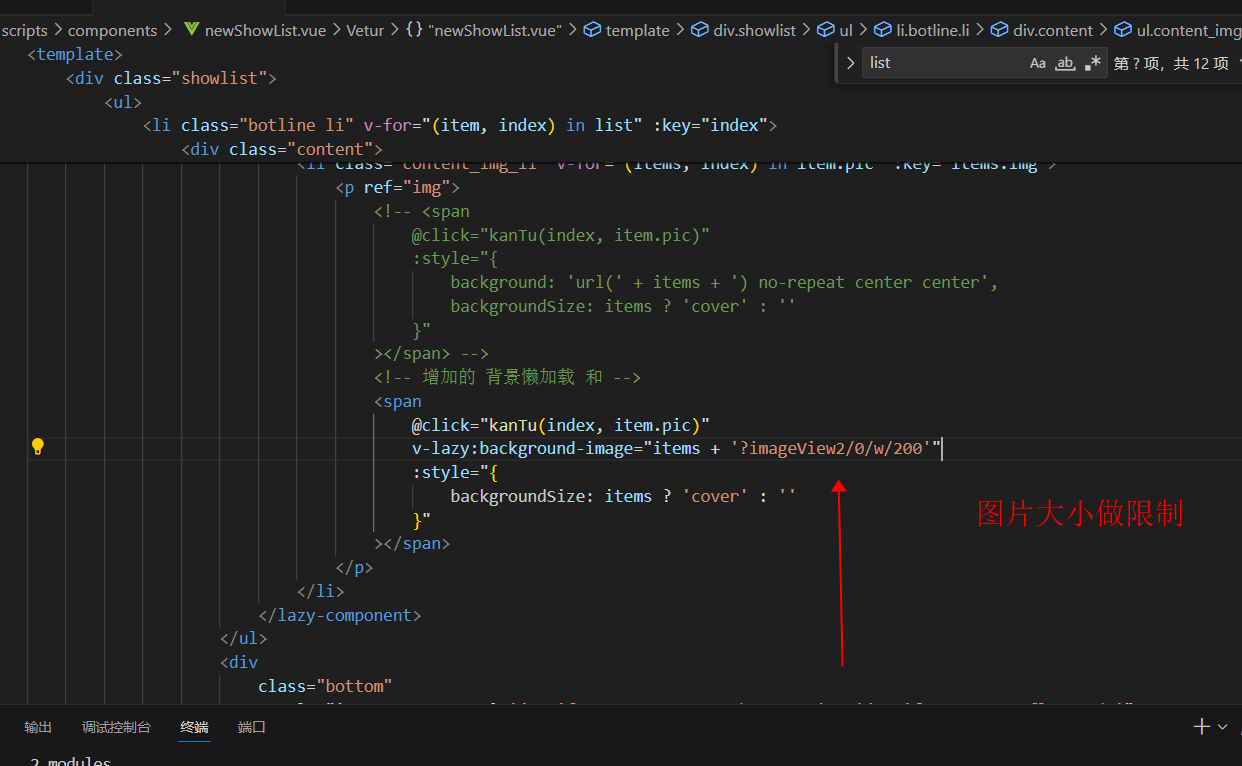
前端 接口返回来的照片太大 加载慢如何解决
现象 解决 1. 添加图片懒加载 背景图懒加载 对背景图懒加载做的解释 和图片懒加载不同,背景图懒加载需要使用 v-lazy:background-image,值设置为背景图片的地址,需要注意的是必须声明容器高度。 <div v-for"img in imageList&quo…...

003 传参
文章目录 传参http 状态码传参方式(1)URL请求参数 key 与 方法中的形参名一致(2)URL请求参数 key与RequestParam("id") 中的别名一致(3) 形参是POJO类,URL 参数 key 与pojo类的 set方…...
)
QT写Windows按键输出(外挂)
一、前言 玩游戏的时候遇到些枯燥无味反反复复的按鼠标键盘的情况时,就想写个外挂自动释放。刚好在学qt所以试验了下QT能不能对外输出按键与鼠标。 二、思路 qt中的按键鼠标全是输入,没有直接对外输出键盘鼠标指令的类,但是我们换个思路&…...

Stable Diffusion之文生图模型训练
1、数据准备 提前准备好一组相关的照片。 在线的图片处理网站 BIRME - Bulk Image Resizing Made Easy 2.0 (Online & Free) 将图片转成统一大小,支持批量处理,效率高 2、生成提示词 进入stable diffusion webui页面 旧版直接使用 train/proproc…...
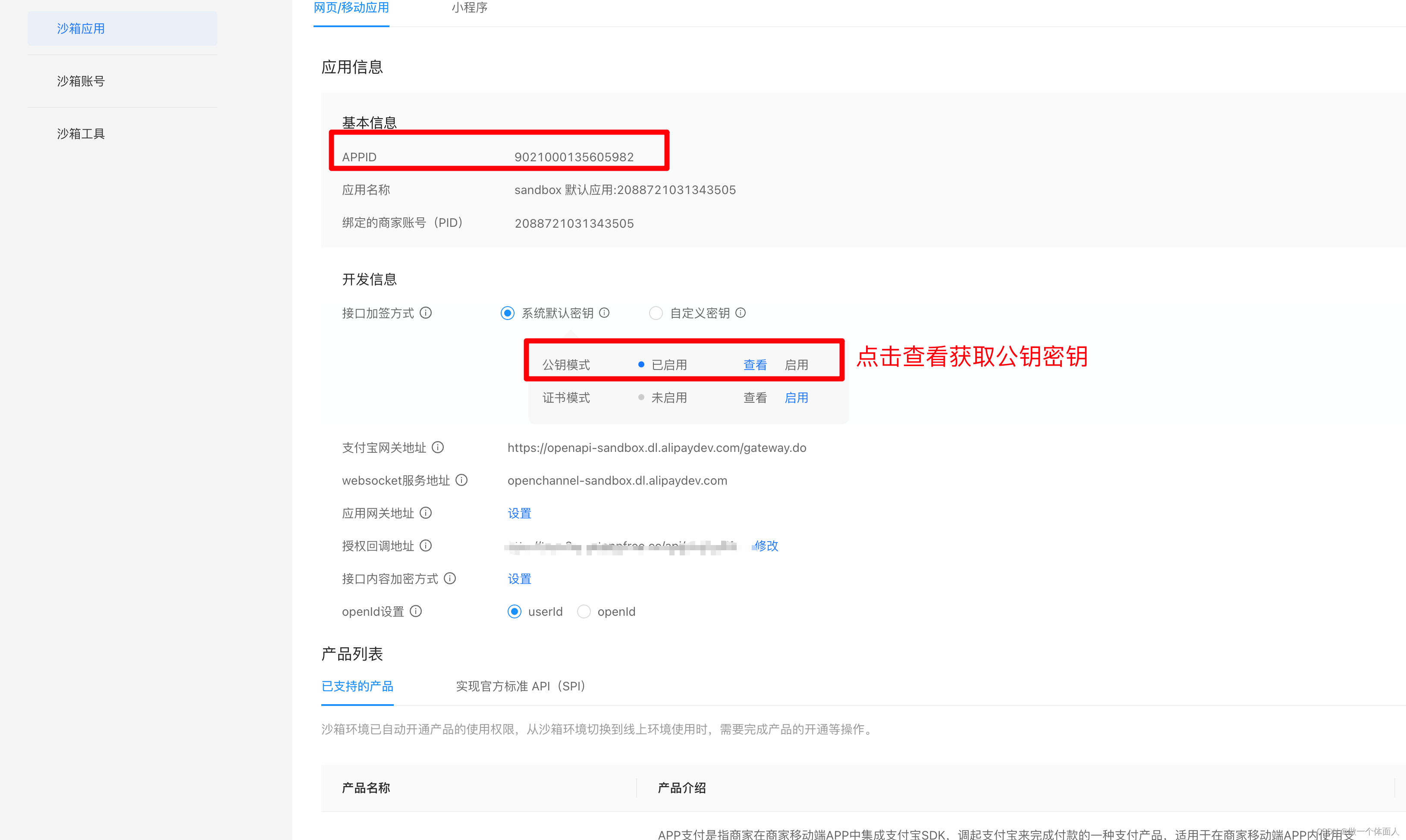
SpringBoot整合支付宝沙箱支付
环境说明:SpringBoot3.0.2 支付宝沙箱地址:沙箱地址 获取配置信息 因支付需要回调地址,回调地址必须是公网,如果有公网的话,那直接在下面配置文件填写自己的公网,没有的话,就需要我们借助第三…...

探索进程控制第一弹(进程终止、进程等待)
文章目录 进程创建初识fork函数fork函数返回值fork常规用法fork调用失败的原因 写时拷贝进程终止进程终止是在做什么?进程终止的情况代码跑完,结果正确/不正确代码异常终止 如何终止 进程等待概述进程等待方法wait方法waitpid 进程创建 初识fork函数 在…...

在mac环境下使用shell脚本实现tree命令
文章目录 使用ls实现tree使用find实现tree 使用ls实现tree 实现思路 使用ls -F 打印文件类型,如果是目录后面跟/,如果是可执行文件后面跟*;使用grep -v /$ 筛选文件排除目录,-v为反向筛选;使用grep /$ 仅筛选目录&am…...

递归时间复杂度分析方法:Master 定理
编写算法时,可能因为对自己代码的复杂度的不清晰而导致错失良机,对于普通的递推或者说循环的代码,仅用简单的调和级数或者等差数列和等比数列即可分析,但是对于递归的代码,简单的递归树法并不方便,理解并记…...

实例名不规范导致mds创建失败
概述 在部署ceph集群时,规划主机名、关闭防火墙、配置免密、关闭selinux,配置hosts文件这几步同样重要,都是初期部署一次麻烦,方便后续运维的动作。遇到过很多前期稀里糊涂部署,后续运维和配置时候各种坑。 近期遇到…...

OpenGL中的纹理过滤GL_NEAREST和GL_LINEAR
一、GL_NEAREST(最近邻插值) 1.1 原理 当需要从纹理中采样颜色时,GL_NEAREST模式会选择离采样点最近的纹理像素(通常是最接近采样点的纹理元素的中心),并直接使用该像素的颜色值作为输出。这种模式不进行任…...

vue 性能优化
data 层级不要太深 data 层级太深会增加响应式监听的计算,导致页面初次渲染时卡顿。 合理使用 v-show 和 v-if 频繁切换时,使用 v-show无需频繁切换时,使用 v-if 合理使用 computed computed 有缓存,data 不变时不会重新计算&…...
互联网大厂ssp面经(操作系统:part1)
1. 什么是进程和线程?它们之间有什么区别? a. 进程是操作系统中运行的一个程序实例。它拥有独立的地址空间和资源,可以独立执行。 b. 线程是进程内的一个执行单元,一个进程可以包含多个线程。 c. 线程共享进程的资源,…...

Android Activity 启动涉及几个进程
Zygote进程: Zygote进程在Android系统启动时被初始创建,并且初始化了虚拟机(Dalvik或ART),预加载了Android系统的核心类库。所有的Android应用进程都是通过fork()从Zygote进程派生出来的,这允许应用快速启动࿰…...

说说你对链表的理解?常见的操作有哪些?
一、是什么 链表(Linked List)是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的,由一系列结点(链表中每一个元素称为结点)组成 每个结点包括两个部分&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 )
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
