蓝桥杯 — —灵能传输
灵能传输
友情链接:灵能传输
题目:


输入样例:
3 3 5 -2 3 4 0 0 0 0 3 1 2 3输出样例:
3 0 3
思路:
题目大意:给出一个数组,每次选择数组中的一个数(要求不能是第一个数与最后一个数),如果这个数是一个正数,就将这个数减去自身两次,并且将相邻的两个数分别加上这个数一次,如果这个数是负数,就将这个数减去自身两次,并且将相邻的数加上这个负数两次,(本质上第二种情况与第一种情况一样,因为减去负数相当于加上这个负数的绝对值),使用公式表述为: a i − 1 + = a i a i + 1 + = a i a i − = 2 a i a_{i - 1} += a_i ~~~~~~~~ a_{i + 1} += a_i~~~~~~~~a_i -= 2a_i ai−1+=ai ai+1+=ai ai−=2ai,并且记住选择的i不能是第一个数或最后一个数。
具体思路:
通过尝试可知,公式与每一个数的前缀和有极大的关系,举例:对于数组5 -2 3 4而言,其前缀和为5 3 6 10,如果选择的是-2,那么原数组的值会变为:3 2 1 4,变化后的数组前缀和为:3 5 6 10,相当于将原数组的前缀和中的第一个位置与第二个位置进行了交换,再看还是对于数组5 -2 3 4而言,如果选择的是3,那么原数组的值会变为5 1 -3 7,对应的前缀和为5 6 3 10,相当于对原数组的前缀和数组的第二个位置与第三个位置进行了交换。下图为更直观的理解:
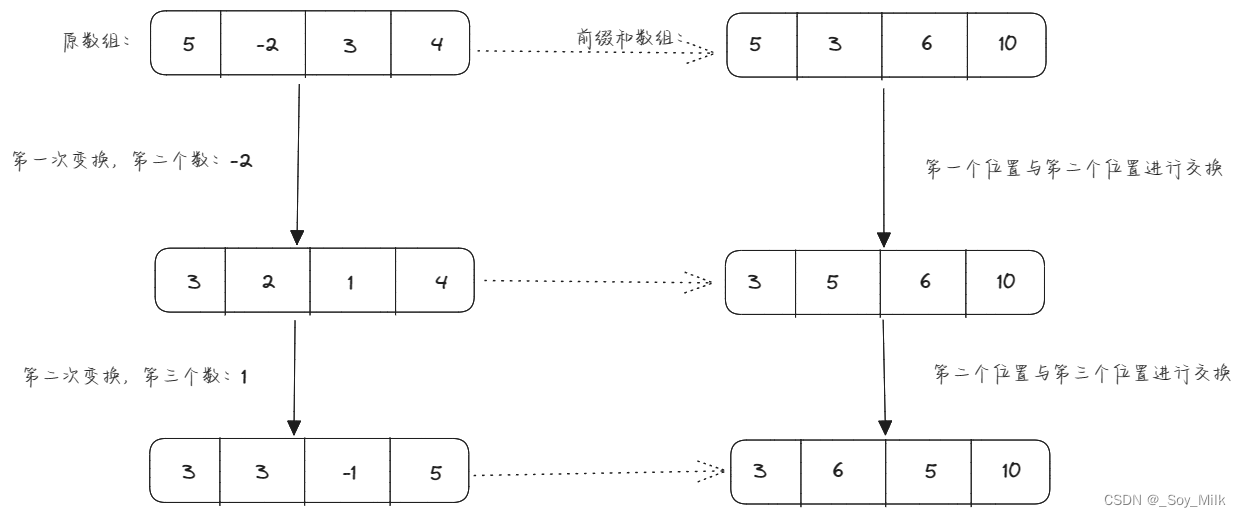
由此我们可以得出一个规律:如果对某一个位置i进行操作,相当于对前缀和数组中i与i - 1位置的值进行交换。其中:1 < i < n。
这样我们就可以得出一个简单的解决方案了,题目要求的是使原数组中数值的绝对值的最大值最小化,一个简单的思路是对前缀和数组进行排序,因为这样可以保证相邻两个前缀和数值的差值最小,这样就保证了原数组中的数值的最大值最小化。
但是题目还有一个条件,就是不能对第一个位置和最后一个位置进行操作,如果直接对前缀和数组(前缀和数组表示为: S S S)进行排序(包含了 S 0 S_0 S0和 S n S_n Sn),那么就违反了题目的要求。我们这样思考:如果对 a 1 a_1 a1(原数组用 a a a表示)进行操作,那么对应的前缀和变化是交换 S 0 S_0 S0和 S 1 S_1 S1(其中 S 0 = 0 S_0 = 0 S0=0 ),如果对 a n a_n an进行操作,那么对应的前缀和数组的变化是交换 S n S_n Sn和 S n − 1 S_{n - 1} Sn−1,为了不使 S 0 S_0 S0和 S n S_n Sn移动,我们这两个数进行移动,我们需要让起点仍然是因为 S 0 S_0 S0和 S n S_n Sn,但为了使相邻两个值之间的差值最小,我们需要使用一些策略:如从 S 0 S_0 S0的位置进行步长为2向前进行取值正序填充到一个新的数组中去并且进行标记,在 S n S_n Sn的位置也进行步长为2向后进行取值,逆序(即:从新数组的最后一个位置开始进行填充)填充到一个新的数组中去并且进行标记,最后从头开始遍历排序后的前缀和数组,将还未标记的值按顺序一次填充到新的数组的空余位置。
还有一个问题: S 0 S_0 S0如果大于 S n S_n Sn该如何解决?
对于这种情况:我们只需要在查找 S 0 S_0 S0和 S n S_n Sn的位置的时候将 S 0 S_0 S0和 S n S_n Sn的位置进行交换即可,这样就变为了 S n S_n Sn向前进行步长为2的取值, S 0 S_0 S0向后进行步长为2的移动。下图为一个直观的理解:

记得要使用long long数据类型,因为int类型的数据最大在 1 0 9 10^9 109左右,而题目要求的 a i a_i ai的值小于等于 1 0 9 10^9 109,其前缀和数组的值可能会超过int的存储容量。
代码:
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
void solve(){int n; cin>>n;vector<ll> A(n + 1, 0);vector<ll> S(n + 1, 0);for(int i = 1;i <= n;i ++){cin>>A[i];S[i] += S[i - 1] + A[i];}// 记录S中的第一个位置与最后一个位置ll front = S[0];ll end = S[n];if(front > end) swap(front, end);// 对前缀和数组进行顺序排序sort(S.begin(), S.end()); // 排序的时候包含了第0个位置的数 // 找到原来S数组的第一个位置和最后一个位置的数在排序后的数组中的下标for(int i = 0;i <= n;i ++){if(S[i] == front){front = i;break;}}for(int i = n;i >= 0;i --){ // 这里遍历也可以从0开始到n结束if(S[i] == end){end = i;break;}}vector<ll> ans(n + 1, 0);// 设定标记数组vector<ll> cnt(n + 1, 0);ll frontidx = 0;ll endidx = n; // 从idxf向前进行找for(int i = front;i >= 0;i -= 2){ans[frontidx++] = S[i];cnt[i] = 1;}// 从idxe向后进行找 for(int i = end;i <=n ;i += 2){ans[endidx --] = S[i];cnt[i] = 1;}// 将剩下的数进行填充 for(int i = 0;i <= n;i ++){if(!cnt[i]){ans[frontidx++] = S[i];}}// 从ans数组中找到相邻两个数之间的最小的值ll tans = 0;for(int i = 1;i <= n;i ++){tans = max(tans, abs(ans[i] - ans[i - 1]));}cout<<tans<<endl;return ;
} signed main(){ios::sync_with_stdio(0);cin.tie(0);int t = 1; cin>>t; // t组询问 while(t--){solve();}return 0;
}
相关文章:

蓝桥杯 — —灵能传输
灵能传输 友情链接:灵能传输 题目: 输入样例: 3 3 5 -2 3 4 0 0 0 0 3 1 2 3输出样例: 3 0 3思路: 题目大意:给出一个数组,每次选择数组中的一个数(要求不能是第一个数与最后一个…...
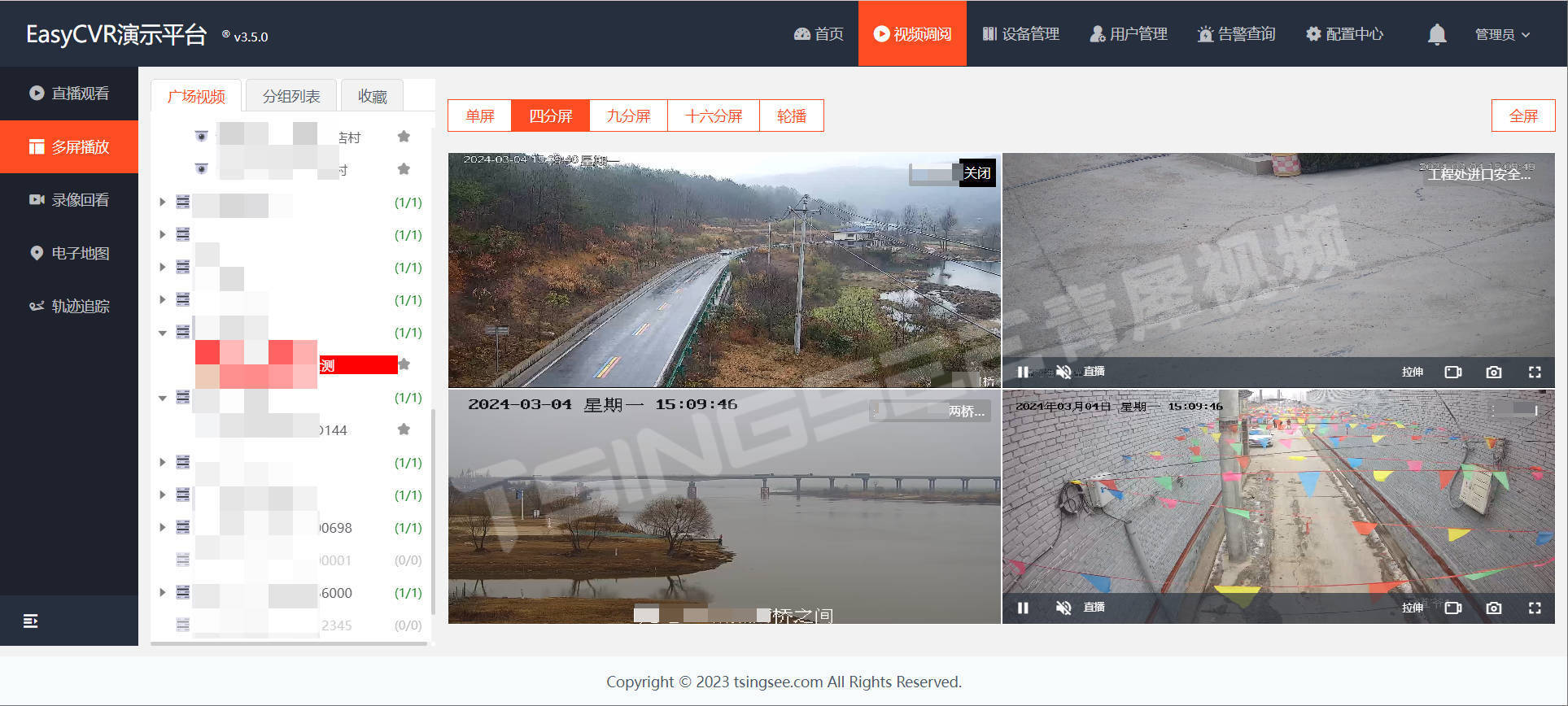
智慧安防系统EasyCVR视频汇聚平台接入大华设备无法语音对讲的原因排查与解决
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台支持7*24小时实时高清视频监控,能同时播放多路监控视频流,视频画面1、4、9、16个可选,支持自定义视频轮播。EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标…...

基于Pytorch框架的CNN-LSTM模型在CWRU轴承故障诊断的应用
目录 1. 简介 2. 方法 2.1数据集 2.2模型架构 1. 简介 CWRU轴承故障诊断是工业领域一个重要的问题,及早发现轴承故障可以有效地减少设备停机时间和维修成本,提高生产效率和设备可靠性。传统的基于信号处理和特征提取的方法通常需要手工设计特征&…...

QQ 邮箱使用 SMTP 发送邮件报错:550 The From header is missing or invalid
文章目录 场景描述问题排查根据提示查看原因查看封装的 message 个人简介 场景描述 QQ 邮箱使用 SMTP 发送邮件报错:550 The From header is missing or invalid: 失败原因:(550, bThe "From" header is missing or invalid. Ple…...

mysql中的视图
1、什么是视图? view:站在不同的角度去看待同一份数据。 2、怎么创建视图对象?怎么删除视图对象? 表复制: mysql> create table dept2 as select * from dept; 创建视图对象: create view dept2_v…...
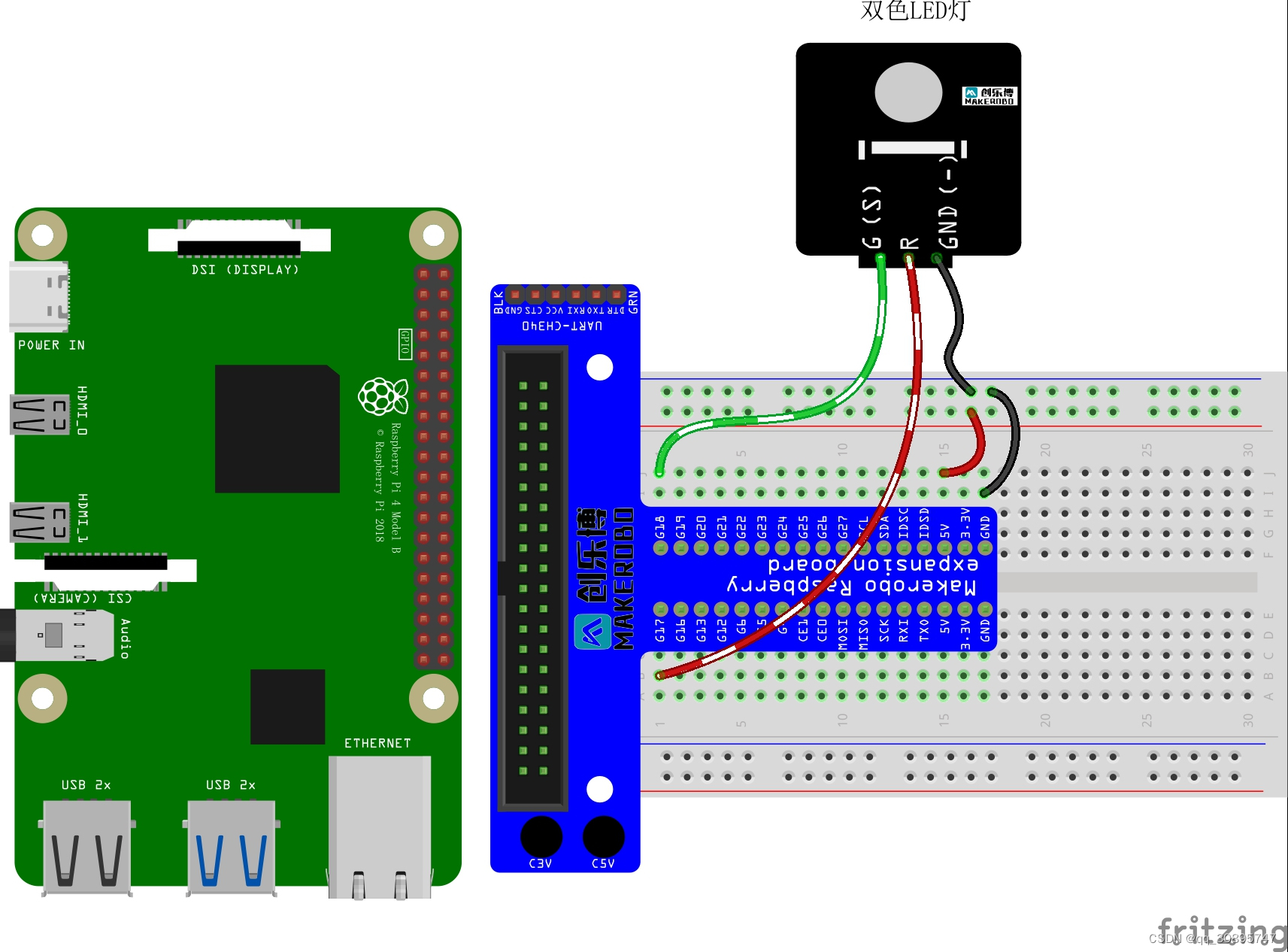
树莓派点亮双色LED
双色LED灯准确来说叫双基色LED灯,是指模块只能显示2种颜色,一般是红色和绿色,可以有三种状态 :灭,颜色1亮,颜色2亮,根据颜色组合的不同,分为红蓝双色,黄蓝双色,红绿双色等等。 接线:将引脚S(绿色)和中间引脚(红色)连接到Raspberry Pi的GPIO接口上,对Raspberry…...

DAY27| 39. 组合总和 ,40.组合总和II ,131.分割回文串
文章目录 39.组合总和40.组合总和II131.分割回文串 39.组合总和 文字讲解:组合总和 视频讲解:组合总和 状态: 此题ok 思路: 代码: class Solution {int sum;public List<List<Integer>> combinationSum(int[] candi…...
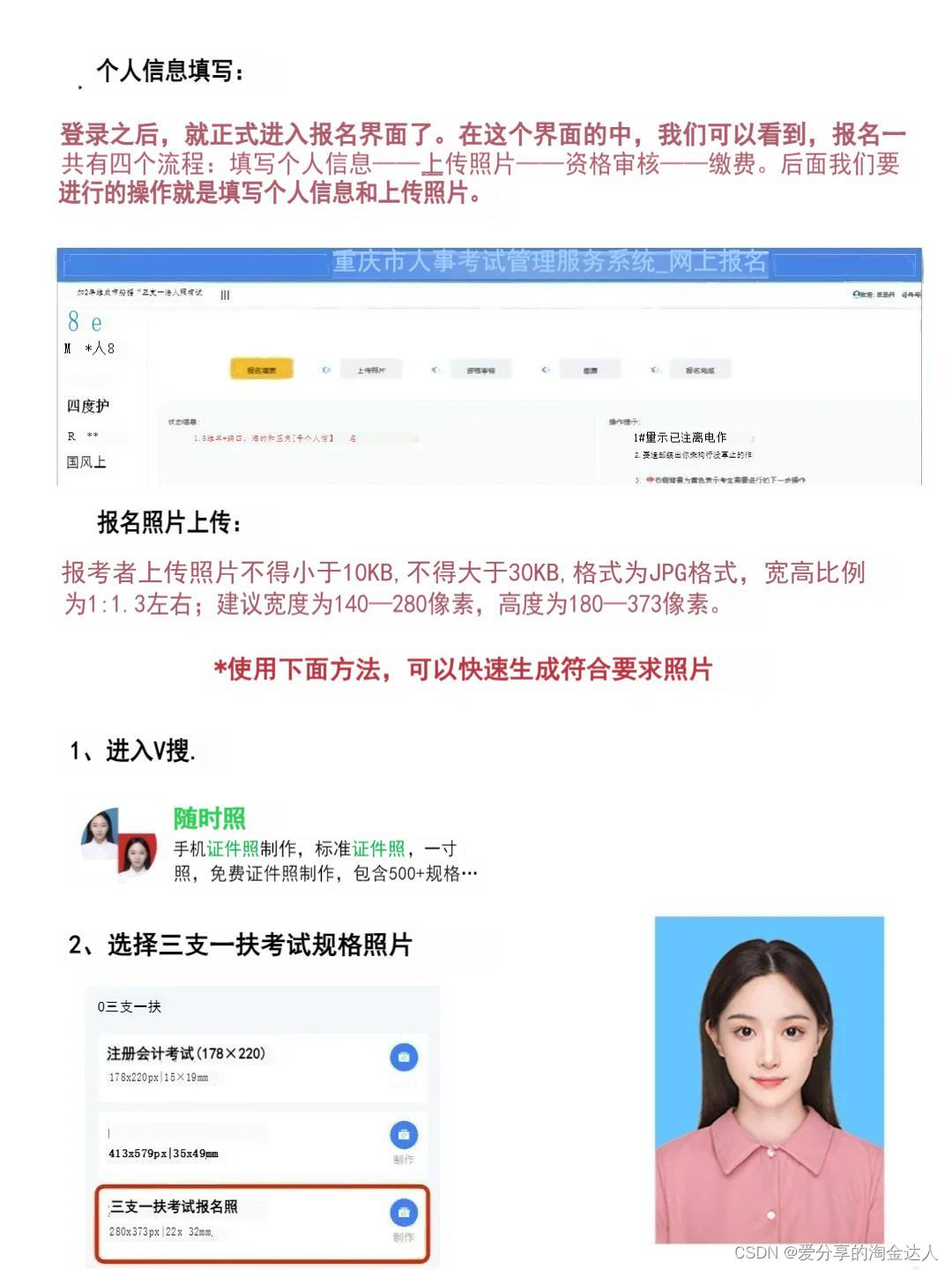
24年重庆三支一扶报名照不通过怎么处理?
24年重庆三支一扶报名照不通过怎么处理?...
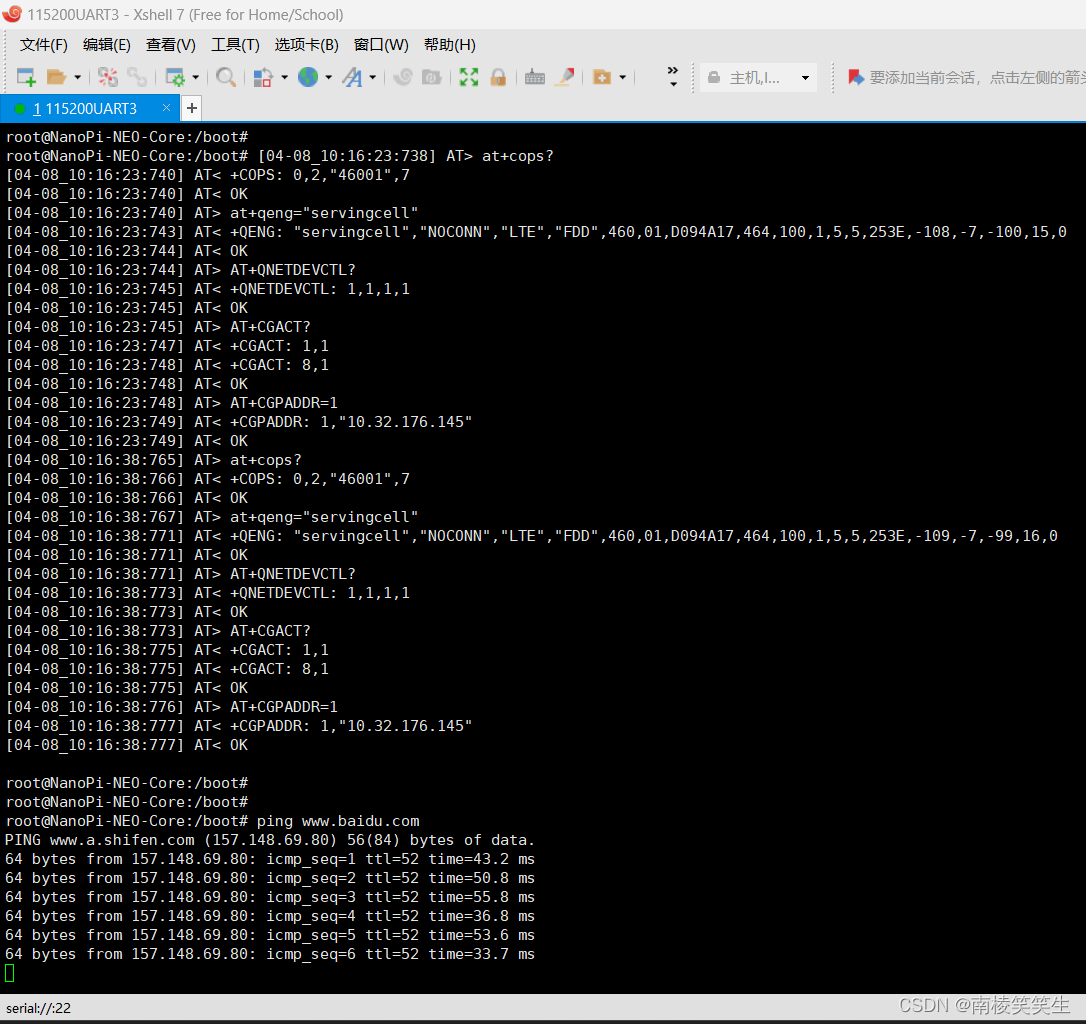
20240409在全志H3平台的Nano Pi NEO CORE开发板上运行Ubuntu Core16.04时跑通4G模块EC200A-CN【PPP模式】
20240409在全志H3平台的Nano Pi NEO CORE开发板上运行Ubuntu Core16.04时跑通4G模块EC200A-CN【PPP模式】 2024/4/9 14:25 【不建议使用ppp模式,功耗大,貌似更过分的!网速还低!】 【唯一的优点:ppp模式下是通过脚本配置…...

【示例】MySQL-不同case下索引的使用分析
前言 本文主要讲述不同SQL语句下,索引的生效情况。 关于索引的前置知识,本文不再讲述。 SQL语句性能分析方法 查看不同类型SQL语句的执行频率 SHOW GLOBAL STATUS LIKE COM_______;慢查询日志 该日志记录了SQL执行时间超过指定参数的所有SQL语句。…...

MySQL表空间管理与优化(8/16)
表空间管理和优化 innodb_file_per_table参数(此参数在分区表章节中还会出现): 这个参数决定了InnoDB表数据的存储方式。当参数设置为ON时,每个InnoDB表的数据会单独存储在一个以.ibd为后缀的文件中,这有利于管理和回收…...

杂货铺 | Linux虚拟机Ubuntu操作系统下设置共享文件夹(以及找不到hgfs文件夹怎么办)
文章目录 📚步骤一:配置共享文件夹📚步骤二:配置挂载环境📚步骤三:解决权限问题📚步骤四:解决重启失效问题 📚步骤一:配置共享文件夹 建立本地共享文件夹&…...

《HF经理》:二认知误区
一、管理者掌握重要权力: 二、全力来自管理者的职位: 三、管理者必须控制自己的直接下属: 对策:展示自己的品质,能力和影响力 四、管理者必须建立良好的个人关系: 五、管理这必须确保一切运行正常&…...
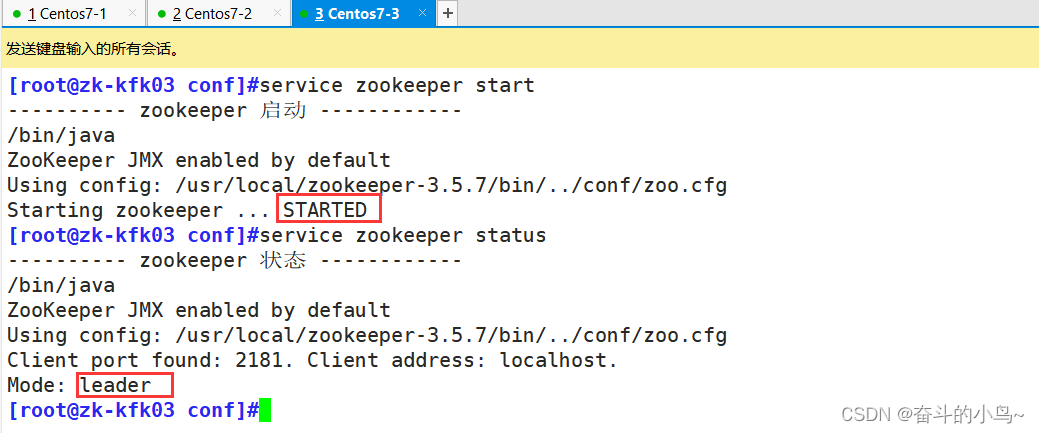
ELK日志分析系统之Zookeeper
一、Zookeeper简介 ZooKeeper是一种为分布式应用所设计的高可用、高性能且一致的开源协调服务,它提供了一项基本服务:分布式锁服务。分布式应用可以基于它实现更高级的服务,实现诸如同步服务、配置维护和集群管理或者命名的服务。 Zookeepe…...
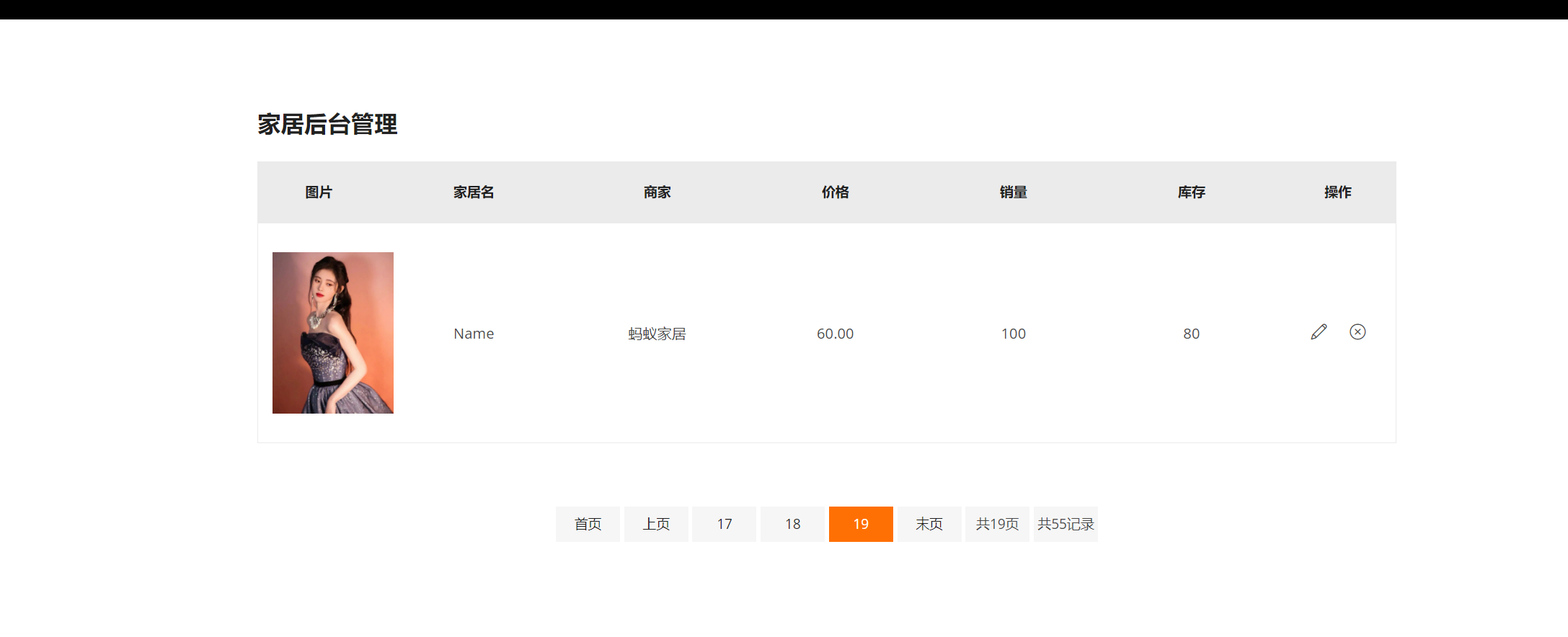
家居网购项目(Ajax验证用户名+上传图片)
文章目录 1.Ajax验证用户名1.程序框架图2.修改MemberServlet3.修改login.jsp4.结果展示 2.Ajax判断验证码是否输入正确1.修改MemberServlet2.修改login.jsp3.结果展示 3.Ajax添加购物车1.程序框架图2.修改CartServlet2.修改index.jsp3.解决问题—未登录直接添加购物车ÿ…...

09 Php学习:超级全局变量
超级全局变量 PHP中预定义了几个超级全局变量(superglobals) ,这意味着它们在一个脚本的全部作用域中都可用。 PHP 超级全局变量列表: $GLOBALS$_SERVER$_REQUEST$_POST$_GET$_FILES$_ENV$_COOKIE$_SESSION $GLOBALS $GLOBALS 是 PHP 中的…...
【Java】SpringBoot快速整合mongoDB
目录 1.什么是mongoDB? 2.Docker安装mongoDB 3.SpringBoot整合mongoDB步骤 4.验证 1.什么是mongoDB? MongoDB是一种非关系型数据库,被广泛用于大型数据存储和分布式系统的构建。MongoDB支持的数据模型比传统的关系型数据库更加灵活&#x…...

UI设计的未来发展
UI 设计的未来发展,实际上是互联网行业未来发展的折射。毕竟,UI 设计始终是互联网行业的一部分,因此在互联网行业未来发展的可能性来看,UI 设计同样会跟随着互联网的部分稳步前进。曾经,在最初的图形化界面出现的时候&…...

推荐系统学习记录——连续的嵌入空间
连续嵌入空间 推荐系统通常会将用户和项目(或商品)表示为向量或嵌入(embeddings),这些向量被映射到一个称为嵌入空间(embedding space)的数学空间中。在这个空间中,相似的用户或项目…...

【Entity Framework】你要知道EF中功能序列与值转换
【Entity Framework】你要知道EF中功能序列与值转换 文章目录 【Entity Framework】你要知道EF中功能序列与值转换一、序列1.1 基本用法1.2 配置序列设置 二、值转换2.1 配置值转换器2.2 批量配置值转换器2.3 预定义的转换2.4 ValueConverter类2.5 内置转换器 三、应用3.1 简单…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
