LeetCode 59.螺旋矩阵II
LeetCode 59.螺旋矩阵II
1、题目
力扣题目链接:59. 螺旋矩阵 II - 力扣(LeetCode)
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入: n = 3
输出: [[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入: n = 1
输出: [[1]]
提示:
1 <= n <= 20
2、模拟
思路
这道题的目的是生成一个按照螺旋顺序填充的二维矩阵。给定一个整数n,它创建一个 n x n 的矩阵,并从左上角开始,按照顺时针方向螺旋填充数字,从1开始,直到填充完整个矩阵(n^2)。
我们可以通过模拟法来顺时针画出螺旋矩阵:
- 填充上边界:从左到右
- 填充右边界:从上到下
- 填充下边界:从右到左
- 填充左边界:从下到上
由外而内填充矩阵。
在这里要注意边界条件,否则很容易蒙圈。
每一圈,我们都要画四条边,每条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
下面按照左闭右开的原则,来画一圈,大家看一下:
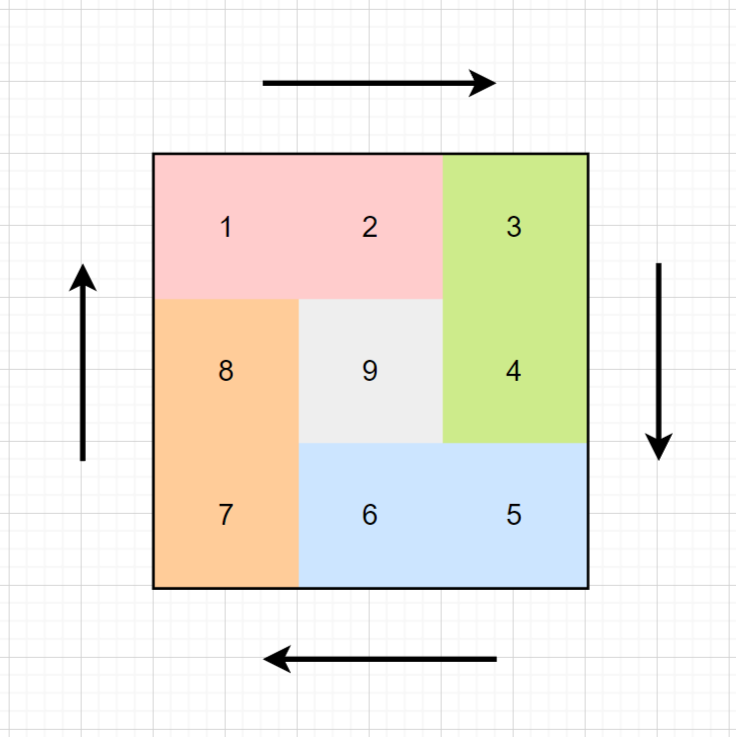
这里每一种颜色,都代表一条边,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。这也是坚持了每条边左闭右开的原则。
代码
class Solution {
public:vector<vector<int>> generateMatrix(int n) {// 初始化一个n x n的二维数组,所有元素初始化为0vector<vector<int>> res(n, vector<int>(n, 0));// 定义螺旋矩阵的起始位置 (startx, starty),也可以理解为横纵坐标int startx = 0, starty = 0;// 循环的次数,n 为奇数时,中间会有一个单独的元素需要单独处理,所以除以2int loop = n / 2;// n为奇数时,中间元素的坐标,例如:n为3, 中间的位置就是(1,1)int mid = n / 2; // 定义当前填充的数字,从 1 开始int count = 1; // 定义每次圈数增加时的偏移量,每次循环右边界收缩一位int offset = 1;int i,j;// 开始螺旋填充,每填充完一圈,loop 减 1while (loop --) {// 当前圈的起始横坐标和纵坐标i = startx;j = starty;// 下面开始的四个for就是模拟转了一圈// 从左到右填充上边界(左闭右开)for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}// 从上到下填充右边界(左闭右开)for (i = startx; i < n - offset; i++) {res[i][j] = count++;}// 从右到左填充下边界(左闭右开)for (; j > starty; j--) {res[i][j] = count++;}// 从下到上填充左边界(左闭右开)for (; i > startx; i--) {res[i][j] = count++;}// 更新下一圈的起始位置,例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)startx++;starty++;// offset 控制每一圈里每一条边遍历的长度offset += 1;}// 如果 n 是奇数,则填充中心位置if (n % 2) {res[mid][mid] = count;}// 返回填充好的螺旋矩阵return res;}
};
复杂度分析
- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
相关文章:

LeetCode 59.螺旋矩阵II
LeetCode 59.螺旋矩阵II 1、题目 力扣题目链接:59. 螺旋矩阵 II - 力扣(LeetCode) 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 示例 1࿱…...

03-JAVA设计模式-适配器模式
适配器模式 设么是适配器模式 它属于结构型模式,主要用于将一个类的接口转换成客户端所期望的另一种接口,从而使得原本由于接口不兼容而无法协同工作的类能够一起工作。 适配器模式主要解决的是不兼容接口的问题。在软件开发中,经常会有这…...
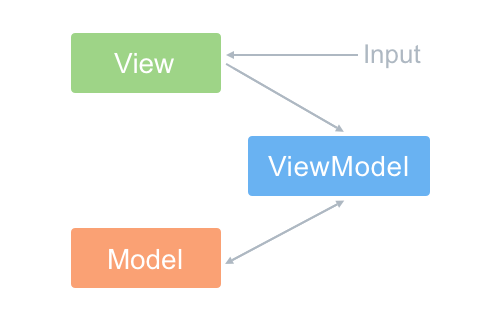
MVVM架构模式
目录 MVVM 数据绑定方式 实现方式 Model View ViewModel 数据绑定方式 vue:: 数据劫持和发布-订阅模式: Object.defineProperty() 方法来劫持(监控)各属性的 getter 、setter ,并在数据(对…...

leetcode2924--找到冠军II
1. 题意 给定一个有向无环图,方向表示胜负关系;求最后胜出的人。 2. 题解 将所有人标记为胜者,统计出度去掉对应胜者标记; 最后统计胜者数目,是否大于1,若大于1,则没有胜者,否则…...
嵌入式|蓝桥杯STM32G431(HAL库开发)——CT117E学习笔记13:RTC实时时钟
系列文章目录 嵌入式|蓝桥杯STM32G431(HAL库开发)——CT117E学习笔记01:赛事介绍与硬件平台 嵌入式|蓝桥杯STM32G431(HAL库开发)——CT117E学习笔记02:开发环境安装 嵌入式|蓝桥杯STM32G431(…...

统一用安卓Studio修改项目包名
可以逃跑,可以哭泣,但不可以放弃 --《鬼灭之刃》 修改项目包名 1)选中项目中药修改的包名: 2)目结构显示方式,取消 Compact Middle Packages 选项; 3)右键要修改的包名,选择 Refactor —— Re…...

Spring Cloud Gateway详细介绍以及实现动态路由
一. 简介 Spring Cloud Gateway This project provides a libraries for building an API Gateway on top of Spring WebFlux or Spring WebMVC. Spring Cloud Gateway aims to provide a simple, yet effective way to route to APIs and provide cross cutting concerns to …...
—— 微调预训练模型)
transformer上手(6)—— 微调预训练模型
1 加载数据集 以同义句判断任务为例(每次输入两个句子,判断它们是否为同义句),构建我们的第一个 Transformers 模型。我们选择蚂蚁金融语义相似度数据集 AFQMC 作为语料,它提供了官方的数据划分,训练集 / …...
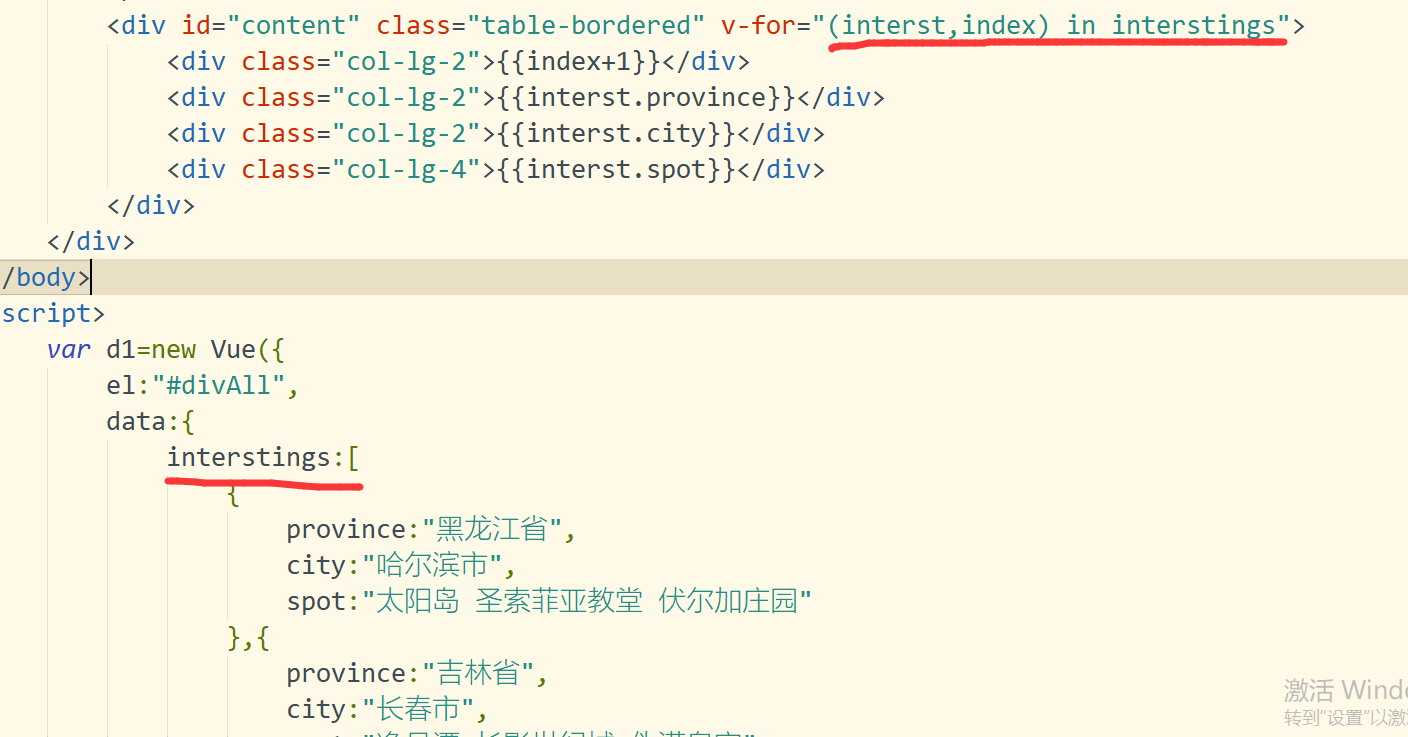
web前端框架设计第四课-条件判断与列表渲染
web前端框架设计第四课-条件判断与列表渲染 一.预习笔记 1.条件判断 1-1:v-if指令:根据表达式的值来判断是否输出DOM元素 1-2:template中使用v-if 1-3:v-else 1-4:v-else-if 1-5:v-show(不支…...
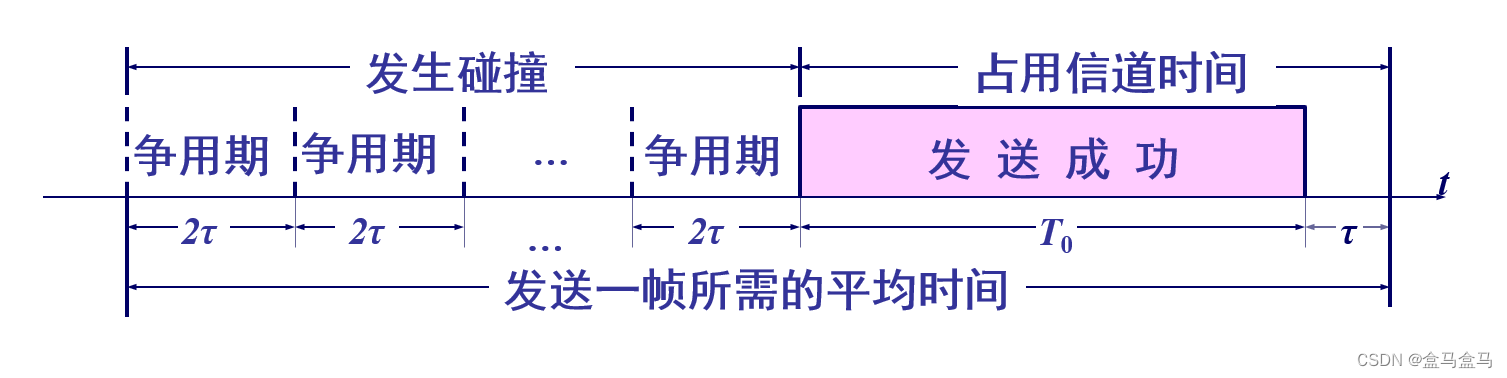
计算机网络:数据链路层 - CSMA/CD协议
计算机网络:数据链路层 - CSMA/CD协议 媒体接入控制CSMA/CD协议截断二进制指数退避算法帧长与帧间间隔信道利用率 媒体接入控制 如图所示,这是一根同轴电缆,有多台主机连接到这根同轴电缆上,他们共享这根传输媒体,形成…...

力扣LeetCode138. 复制带随机指针的链表 两种解法(C语言实现)
目录 题目链接 题目分析 题目定位: 解题思路 解题思路1(粗暴但是复杂度高) 解题思路2(巧妙并且复杂度低) 题目链接 138. 复制带随机指针的链表https://leetcode-cn.com/problems/copy-list-with-random-pointer/ …...

强大的压缩和解压缩工具 Keka for Mac
Keka for Mac是一款功能强大的压缩和解压缩工具,专为Mac用户设计。它支持多种压缩格式,包括7z、Zip、Tar、Gzip和Bzip2等,无论是发送电子邮件、备份文件还是节省磁盘空间,Keka都能轻松满足用户需求。 这款软件的操作简单直观&…...
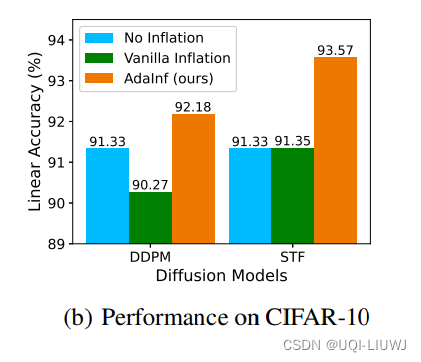
论文速读:Do Generated Data Always Help Contrastive Learning?
在对比学习领域,最近很多研究利用高质量生成模型来提升对比学习 给定一个未标记的数据集,在其上训练一个生成模型来生成大量的合成样本,然后在真实数据和生成数据的组合上执行对比学习这种使用生成数据的最简单方式被称为“数据膨胀”这与数据…...
华为欧拉系统(openEuler-22.03)安装深信服EasyConnect软件(图文详解)
欧拉镜像下载安装 iso镜像官网下载地址 选择最小化安装,标准模式 换华为镜像源 更换华为镜像站,加速下载: sed -i "s#http://repo.openeuler.org#https://mirrors.huaweicloud.com/openeuler#g" /etc/yum.repos.d/openEuler.r…...

git commit --amend用法
一、git commit --amend 修改提交信息:您可以使用 git commit --amend 命令来修改最新提交的提交信息。执行该命令后,Git 将会打开文本编辑器(通常是的默认文本编辑器),以便编辑提交信息。完成编辑后保存并关闭编辑器…...
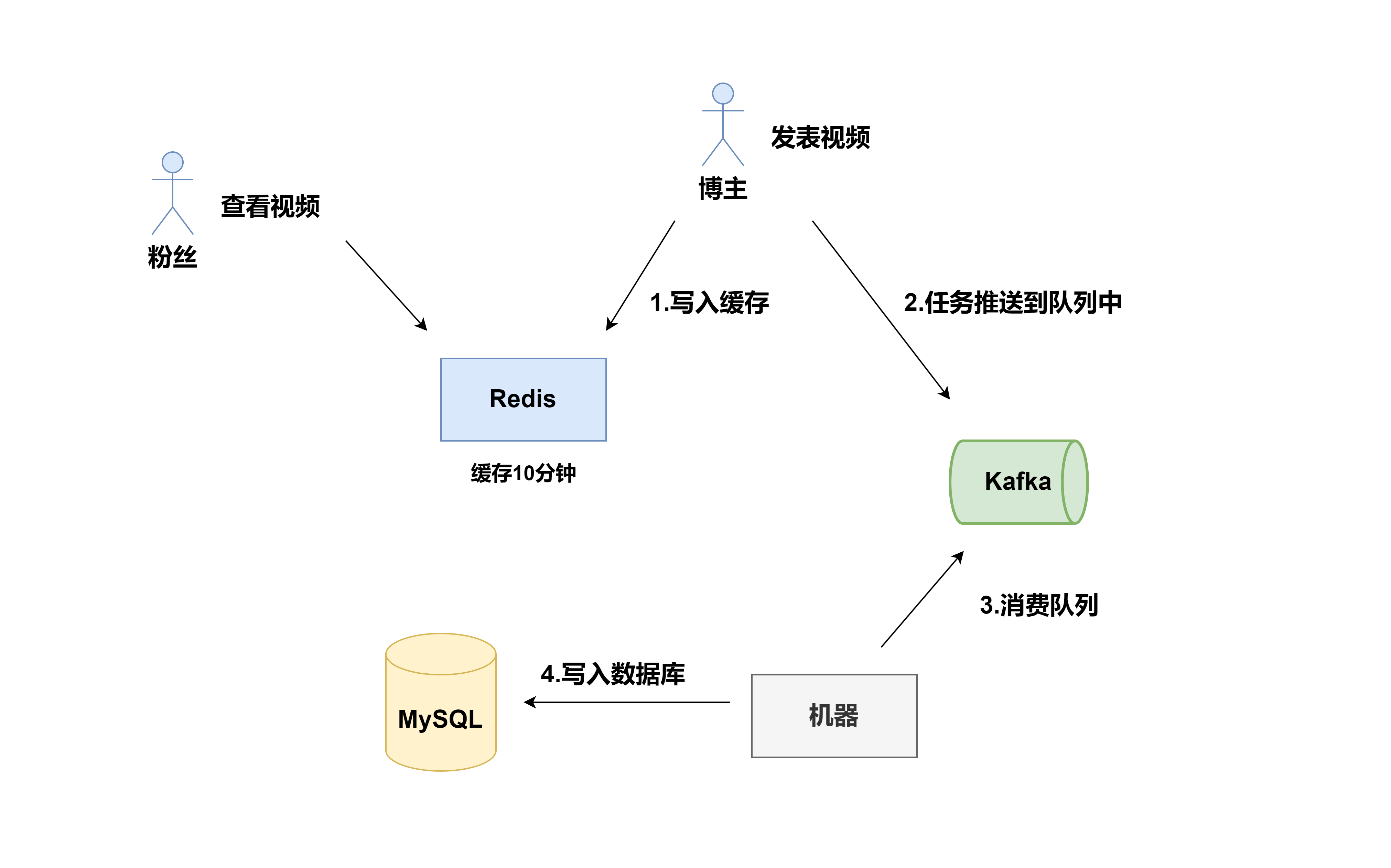
分布式系统:缓存与数据库一致性问题
前言 缓存设计是应用系统设计中重要的一环,是通过空间换取时间的一种策略,达到高性能访问数据的目的;但是缓存的数据并不是时刻存在内存中,当数据发生变化时,如何与数据库中的数据保持一致,以满足业务系统…...

JavaEE企业开发新技术5
目录 2.18 综合应用-1 2.19 综合应用-2 2.20 综合应用-3 2.21 综合应用-4 2.22 综合应用-5 Synchronized : 2.18 综合应用-1 反射的高级应用 DAO开发中,实体类对应DAO的实现类中有很多方法的代码具有高度相似性,为了提供代码的复用性,降低…...

mysql dump导出导入数据
前言 mysqldump是MySQL数据库中一个非常有用的命令行工具,用于备份和还原数据库。它可以将整个数据库或者特定的表导出为一个SQL文件,以便在需要时进行恢复或迁移。 使用mysqldump可以执行以下操作: 备份数据库:可以使用mysqld…...

刷题记录3
# 10 字符个数统计 描述 编写一个函数,计算字符串中含有的不同字符的个数。字符在 ASCII 码范围内( 0~127 ,包括 0 和 127 ),换行表示结束符,不算在字符里。不在范围内的不作统计。多个相同的字符只计算一次 例如,对…...
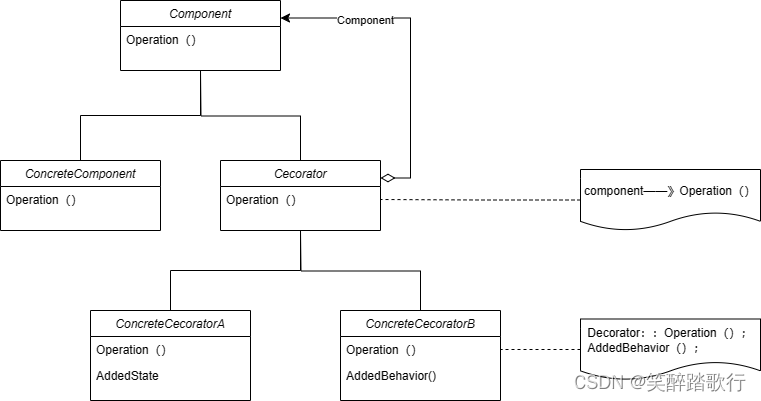
Decorator 装饰
意图 动态的给一个对象添加一些额外的职责。就增加功能而言,Decorator模式比生成子类更加灵活 结构 其中: Component定义一个对象接口,可以给这些对象动态的添加职责。ConcreteComponent定义一个对象,可以给这个对象添加一些职…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
