Java二叉树(2)
一、二叉树的链式存储
二叉树的存储分为顺序存储和链式存储
(本文主要讲解链式存储)
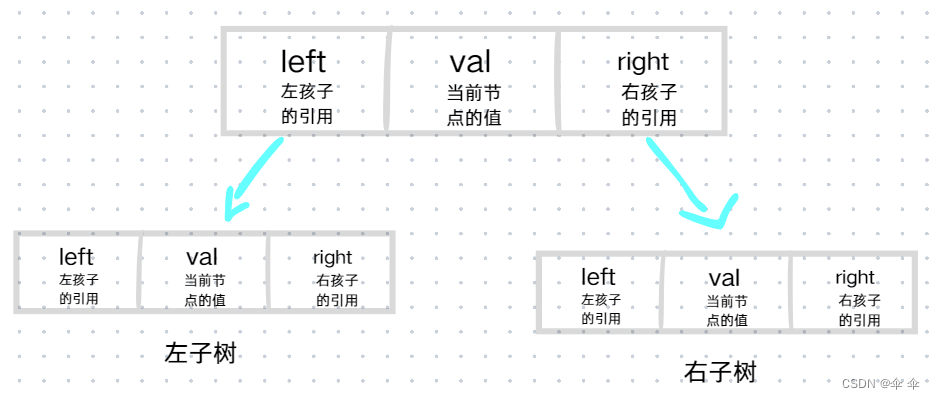
二叉树的链式存储是通过一个一个节点引用起来的,常见的表示方式有二叉三叉
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}
孩子双亲表示法在后续介绍,本文采用孩子表示法来构建二叉树
二、二叉树的遍历
前序遍历:根 左 右
中序遍历:左 根 右
后序遍历:左 右 根
层序遍历:从上到下 从左到右 依次遍历
所有的遍历都是沿着某条路线进行的
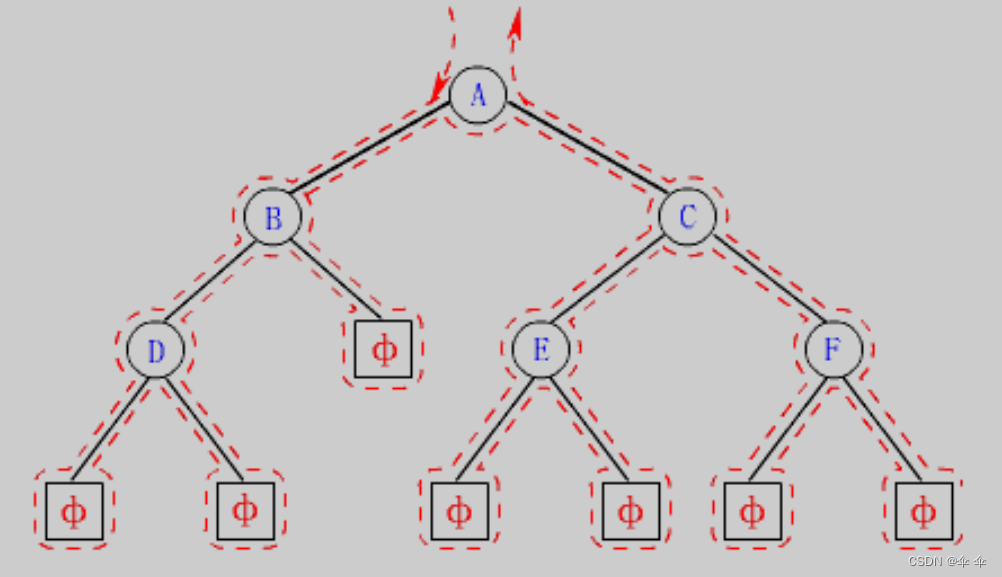
上图二叉树的各遍历分别是:
前序:A B D C E F
中序:D B A E C F
后序:D B E F C A
层序:A B C D E F
例题:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
题解:
前序:ABDHECFG
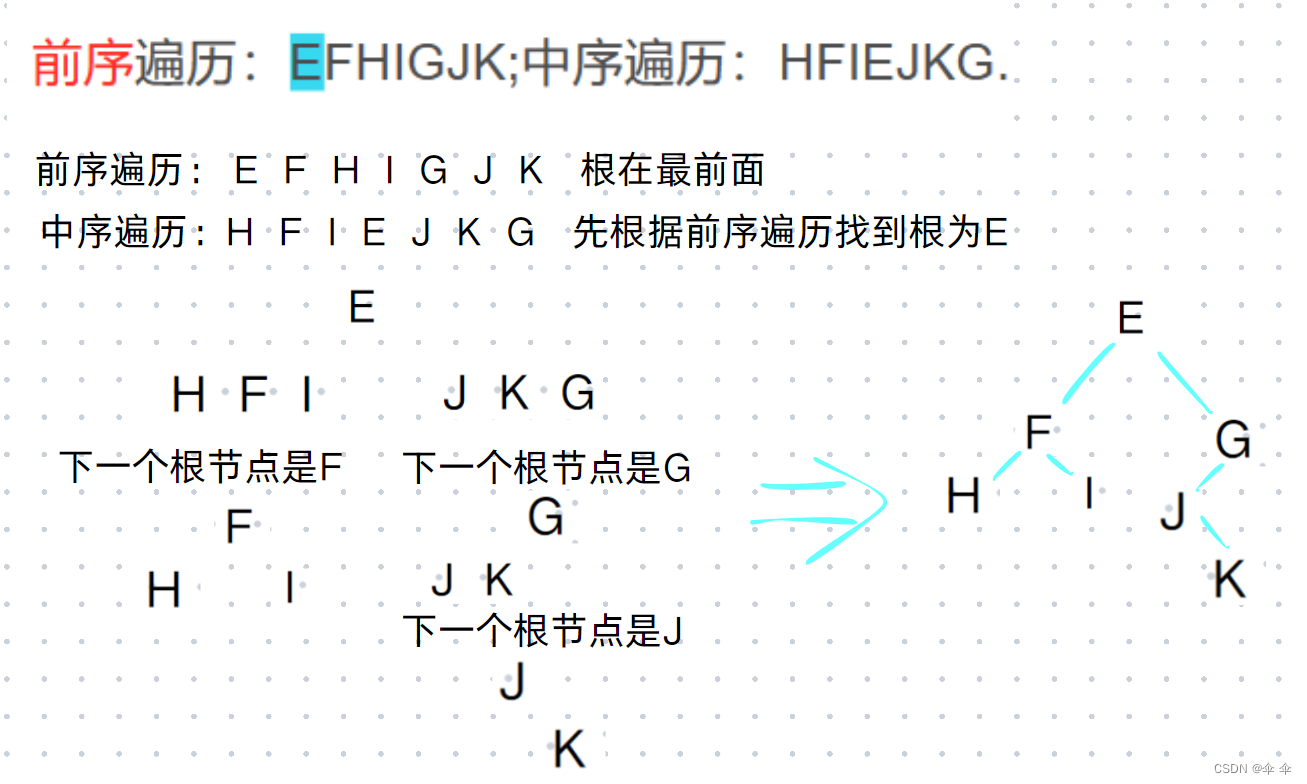
2.二叉树的前序遍历和中序遍历如下:前序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H
题解:
后序遍历:H I F K J G E
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde
题解:
前序遍历:a b c d e
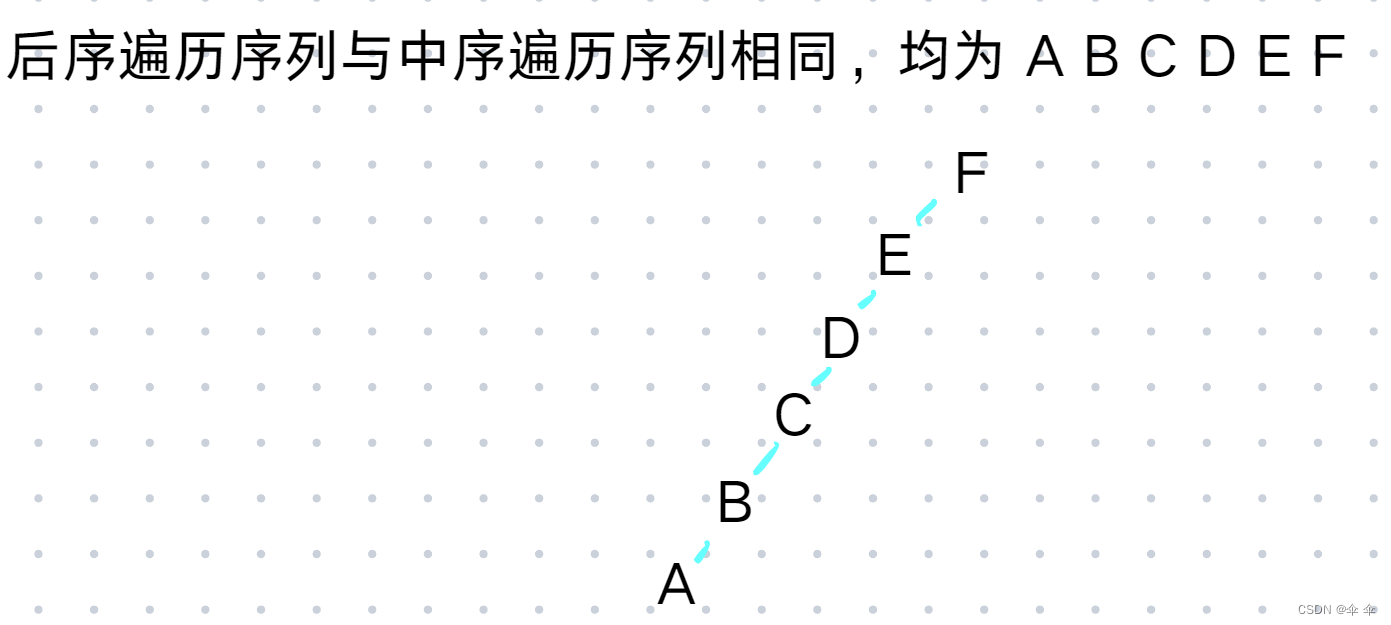
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
题解:
根据前几道题目的方法能画出二叉树:
层序遍历:F E D C B A
注意:根据前序和后序不能创建二叉树,只能确定根的位置,无法确定左右子树的位置
三、二叉树的基本操作与图解
public class MyBinaryTree {static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val){this.val = val;}}public TreeNode createTree(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;//根节点}// 前序遍历void preOrder(TreeNode root){if(root == null){return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍历void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}//节点个数public int size(TreeNode root){if(root==null){return 0;}int ret = size(root.left)+size(root.right)+1;return ret;//子问题思路}public int nodeSize;public void size2(TreeNode root){if(root==null){return ;}nodeSize++;size2(root.left);size2(root.right);}//整棵树的叶子节点个数public int getLeafNodeCount(TreeNode root){if(root==null){return 0;}//左子树的叶子节点+右子树的叶子节点就是整棵树的叶子if(root.left==null&&root.right==null){return 1;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}//遍历思路public int leafSize;public void getLeafNodeCount2(TreeNode root){if(root==null){return ;}//左子树的叶子节点+右子树的叶子节点就是整棵树的叶子if(root.left==null&&root.right==null){leafSize++;}getLeafNodeCount2(root.left);getLeafNodeCount2(root.right);}// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k){if(root==null){return 0;}if(k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}// 获取二叉树的高度int getHeight(TreeNode root){if(root==null){return 0;}//整棵树的高度=左树高度和右树高度的最大值+1int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;}// 检测值为value的元素是否存在TreeNode find(TreeNode root, int val){if(root==null){return null;}if(root.val==val){return root;}TreeNode ret = find(root.left,val);if(ret !=null){return root;}ret = find(root.right,val);if(ret !=null){return root;}return null;}
}
递归遍历代码讲解:以前序遍历为例

求节点个数代码图解:

获取k层节点的个数图解:
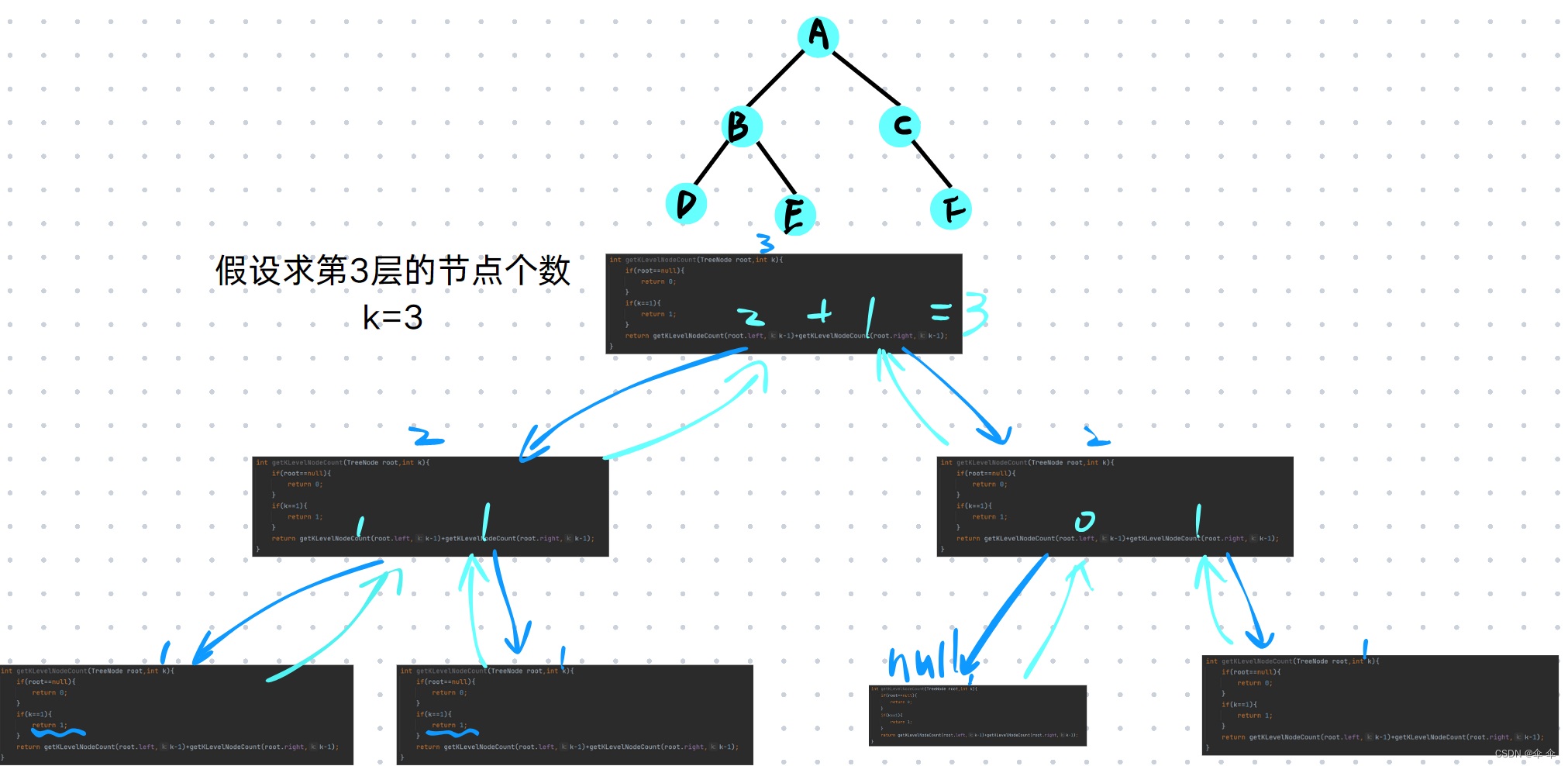 获取二叉树的高度图解:
获取二叉树的高度图解:
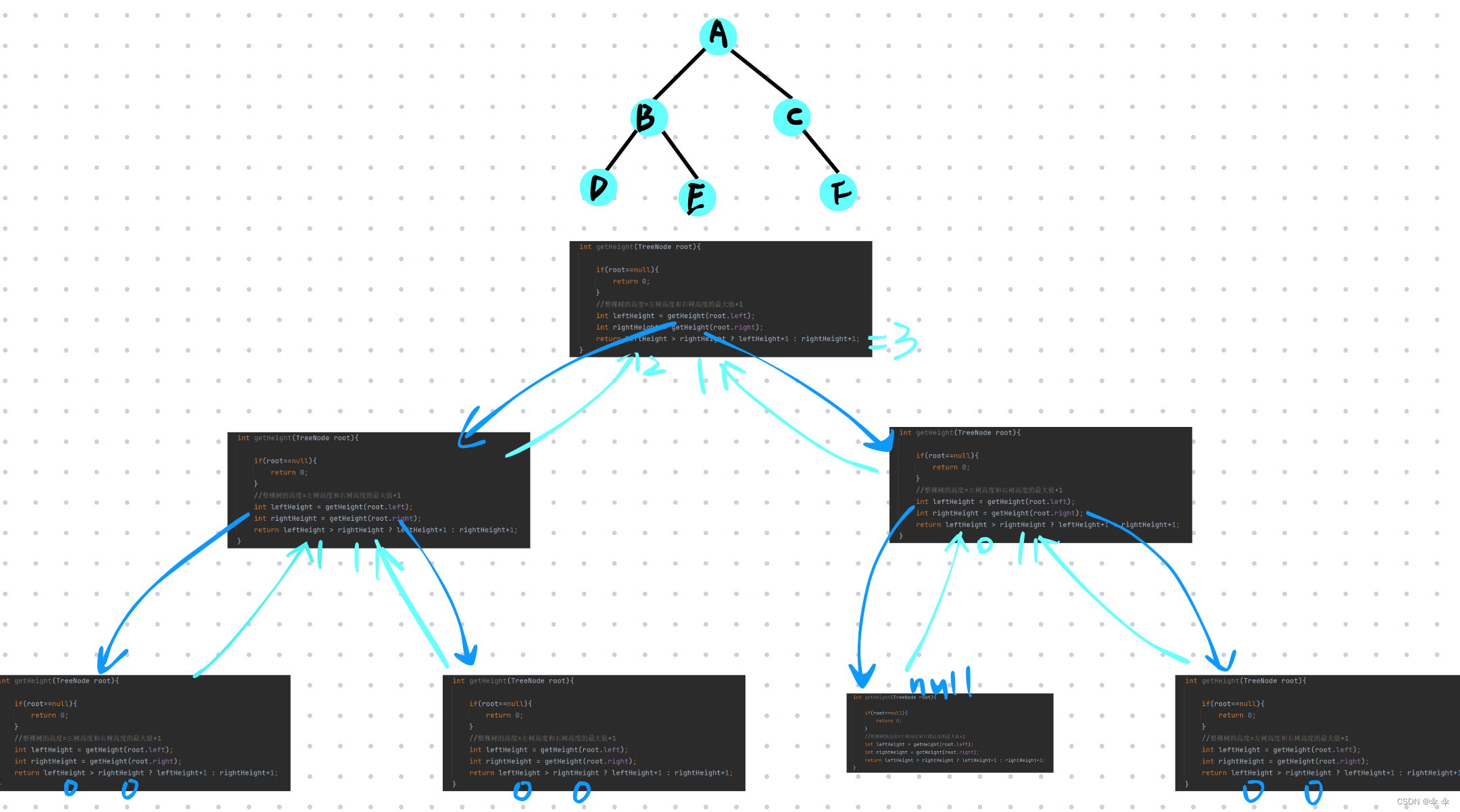
检测为value的值是否存在图解:

相关文章:

Java二叉树(2)
一、二叉树的链式存储 二叉树的存储分为顺序存储和链式存储 (本文主要讲解链式存储) 二叉树的链式存储是通过一个一个节点引用起来的,常见的表示方式有二叉三叉 // 孩子表示法 class Node { int val; // 数据域 Node left; // 左孩子的引用…...

关于AG32 MCU的一些奇思妙想
1、AG32VF103的网口是100M还是10M? RE: 都是100M的。 2、用FPGA能不能再仿出一个网口?有些产品用到两个网口。 理论上可以,但是要考虑,一个是cpld实现难度,一个是需要的逻辑单元。因为mac逻辑多,内置的2KL…...

除了sql外还有那些查询语言
除了SQL(结构化查询语言)外,还有许多其他的查询语言,包括但不限于XQuery(对XML的查询语言)、MDX(多维查询语言,用于分析数据仓库)、DQL(数据查询语言…...
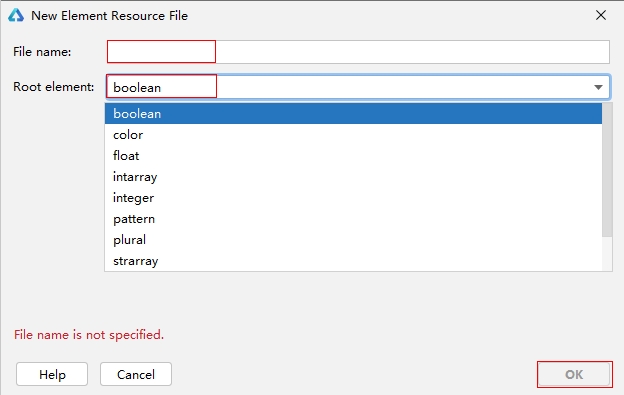
构建第一个ArkTS用的资源分类与访问
应用开发过程中,经常需要用到颜色、字体、间距、图片等资源,在不同的设备或配置中,这些资源的值可能不同。 应用资源:借助资源文件能力,开发者在应用中自定义资源,自行管理这些资源在不同的设备或配置中的表…...

JVM中都有哪些引用类型
● 强引用:JVM中默认引用关系就是强引用,即是对象被局部变量、静态变量等GC Root关联的对象引用,只要这层关系存在,普通对象就不会被回收 ● 软引用:软引用相对于强引用是一种比较弱的引用关系,如果一个对象…...

分布式锁-Redission快速入门
实战篇Redis 5、分布式锁-redission 5.2 分布式锁-Redission快速入门 引入依赖: <dependency><groupId>org.redisson</groupId><artifactId>redisson</artifactId><version>3.13.6</version> </dependency>配置…...

IDEA 本地库引入了依赖但编译时找不到
在使用 IDEA 开发 Maven 项目的过程中,有时会遇到本地库引入了依赖,但编译时报找不到这个依赖,可以使用命令处理。 打开 Terminal。 执行清理命令。 mvn clean install -Dmaven.test.skiptrue执行更新命令。 mvn -U idea:idea...

hadoop最新详细版安装教程 2024 最新版
文章目录 hadoop安装教程 2024最新版提前准备工作用户配置安装 SSH Server免密登录设置编辑 SSH server 配置文件配置Java环境查看java 版本验证 环境变量设置安装Hadoop下载hadoop解压hadoop查看hadoop 版本hadoop 配置编辑编辑配置文件core-site.xml编辑配置文件hdfs-site.xm…...

Unity 中画线
前言: 在Unity项目中,调试和可视化是开发过程中不可或缺的部分。其中,绘制线条是一种常见的手段,可以用于在Scene场景和Game视图中进行调试和展示。本篇博客将为你介绍多种不同的绘制线条方法,帮助你轻松应对各种调试…...
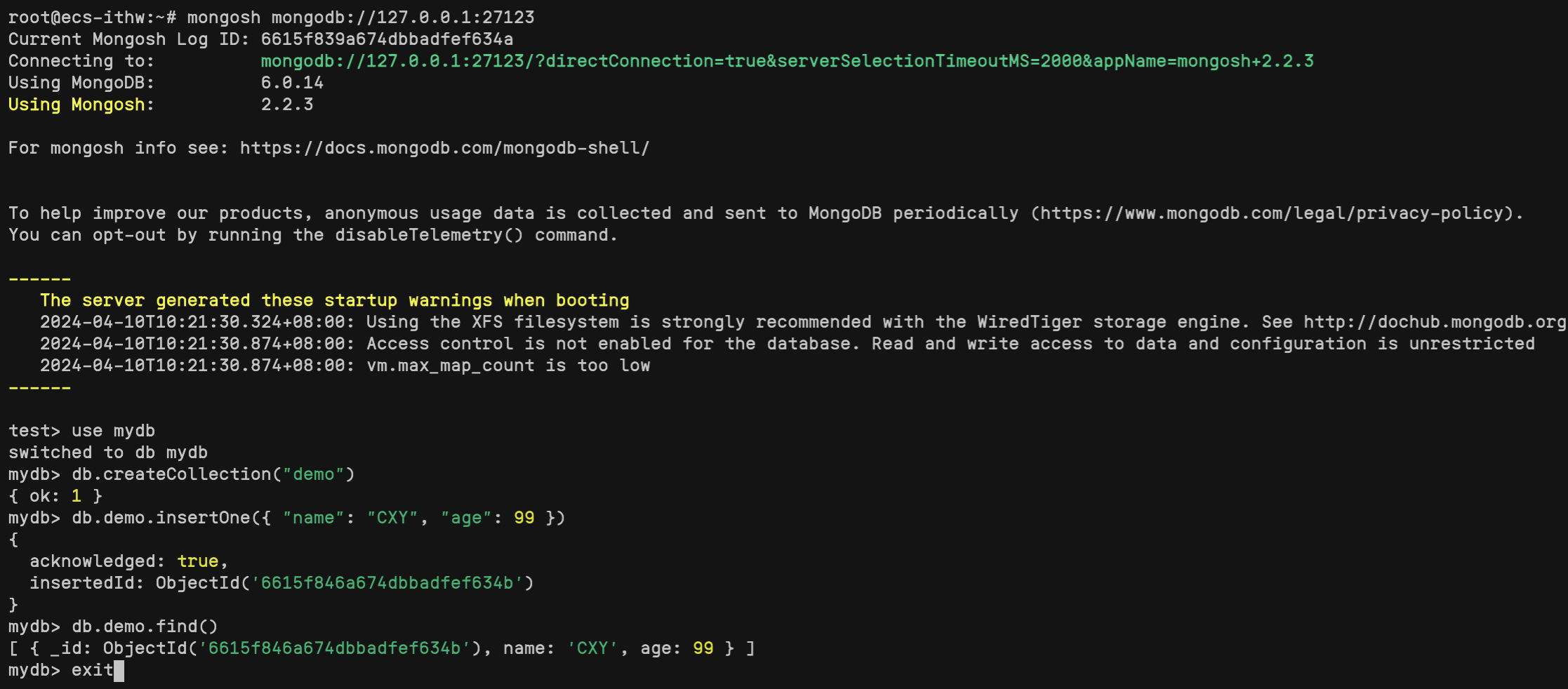
【快捷部署】017_MongoDB(6.0.14)
📣【快捷部署系列】017期信息 编号选型版本操作系统部署形式部署模式复检时间017MongoDB6.0.14Ubuntu 20.04apt单机2024-04-11 一、快捷部署 #!/bin/bash ################################################################################# # 作者:…...

Android中的Zygote进程介绍
在Android系统中,Zygote是一个特殊的进程,主要负责孵化(fork)新的应用进程,从而加速应用的启动过程。Zygote进程是系统启动过程中创建的第一个进程,它会在系统启动时被初始化并一直运行在后台。 以下是Zyg…...

世界需要和平--中介者模式
1.1 世界需要和平 "你想呀,国与国之间的关系,就类似于不同的对象与对象之间的关系,这就要求对象之间需要知道其他所有对象,尽管将一个系统分割成许多对象通常可以增加其可复用性,但是对象间相互连接的激增又会降低…...

PHPStudy(小皮)切换PHP版本PDO拓展失效的问题
因为要看一个老项目,PHP版本在8.0以上会报错,只能切换到7.2,但又遇到了PDO没开启的问题。 PHPStudy上安装的PHP7.2是需要自己配置一下的,里面php.ini文件是空的,需要将php.ini-development改成php.ini,对于…...
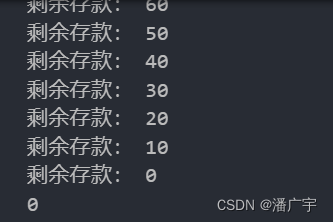
Golang 基于共享变量的并发锁
一、互斥锁 先看一个并发情况,同时操作一个全局变量,如果没有锁会怎么样 假设有1000个goroutines并发进行银行余额的扣除,每次都扣除10元,起始的总余额是10000,理论上并发执行完应该是0对不对,但实际却不…...
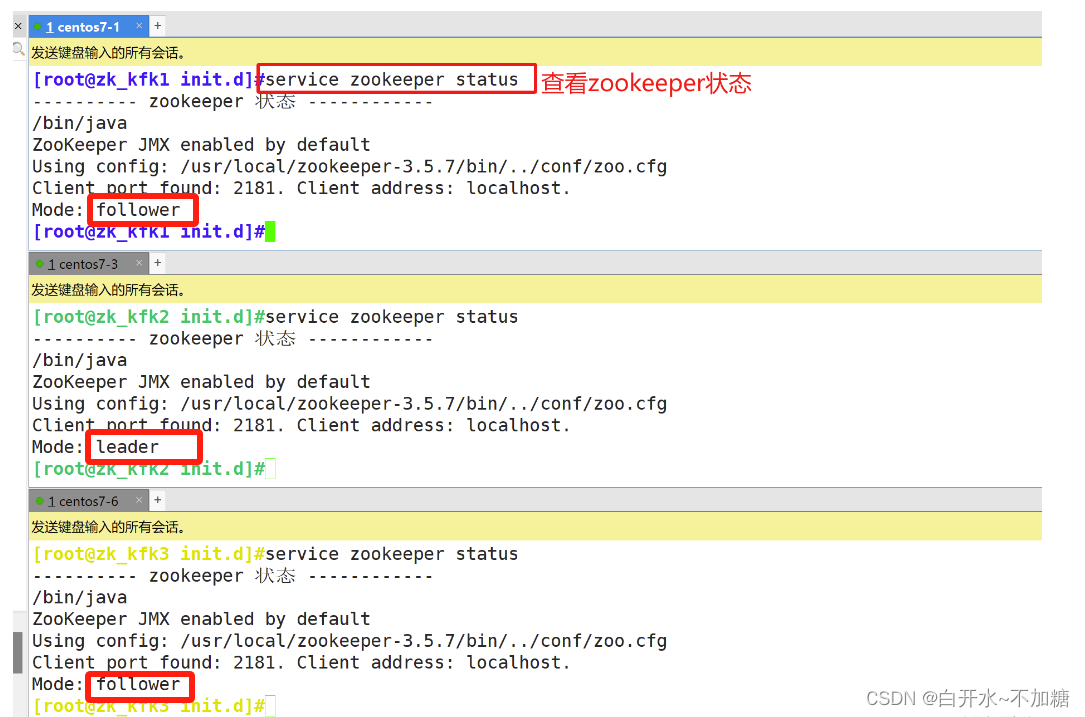
探索分布式技术--------------注册中心zookeeper
目录 一、ZooKeeper是什么 二、ZooKeeper的工作机制 三、ZooKeeper特点 四、ZooKeeper数据结构 五、ZooKeeper应用场景 5.1统一命名服务 5.2统一配置管理 5.3统一集群管理 5.4服务器动态上下线 5.5软负载均衡 六、ZooKeeper的选举机制 6.1第一次启动选举机制 6.2非…...
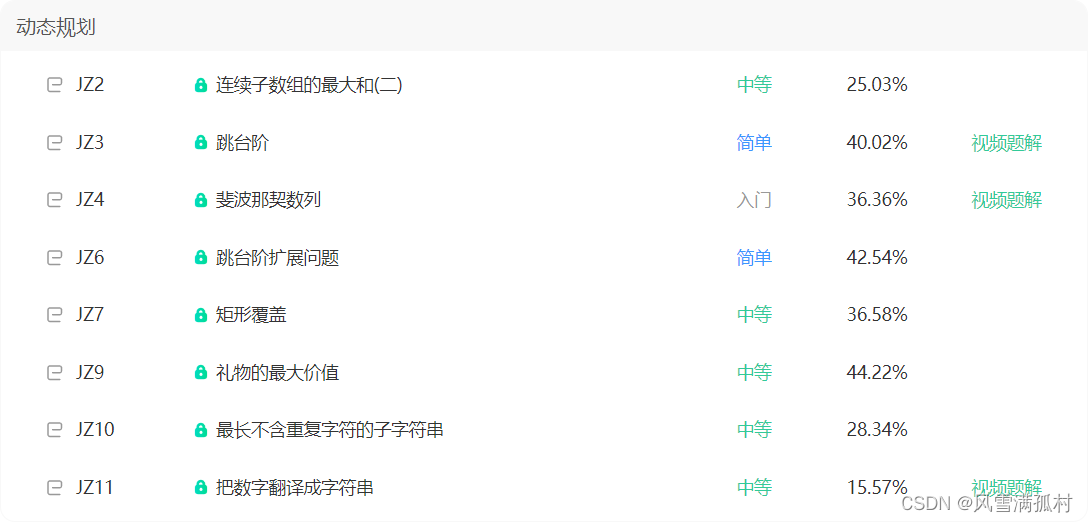
剑指offer之牛客与力扣——前者分类题单中的题目在后者的链接
搜索 [4.12完成] JZ1 LCR 172. 统计目标成绩的出现次数 JZ3 153. 寻找旋转排序数组中的最小值 JZ4 LCR 014. 字符串的排列 JZ5 LCR 163. 找到第 k 位数字 400 动态规划 [4.15完成] JZ2 LCR 161. 连续天数的最高销售额 53 JZ3 LCR 127. 跳跃训练 70 JZ4 LCR 126. 斐波那契…...

C# WinForm —— 05 控件简介
简介 窗体中用于输入或操作的对象,有自己的属性、方法、事件 属性:外观方法:功能事件:行为控制特征 可视化,与用户进行交互,属性,方法,事件,可供开发人员使用࿰…...
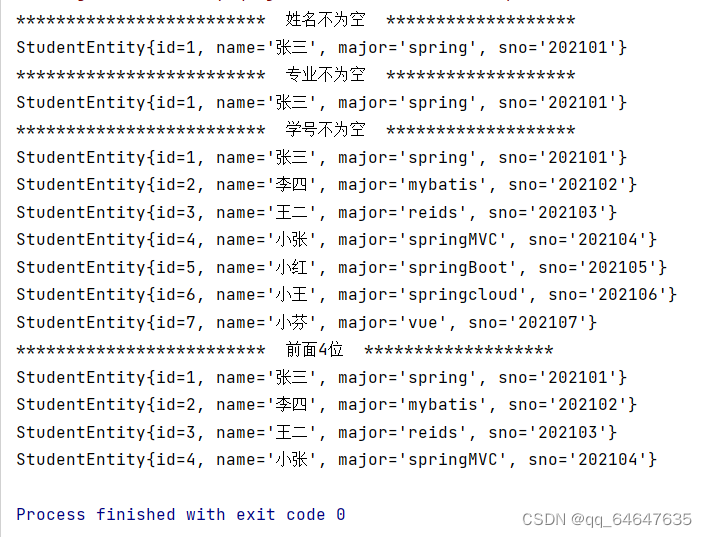
JavaEE实验三:3.5学生信息查询系统(动态Sql)
题目要求: 使用动态SQL进行条件查询、更新以及复杂查询操作。本实验要求利用本章所学知识完成一个学生信息系统,该系统要求实现3个以下功能: 1、多条件查询: 当用户输入的学生姓名不为空,则根据学生姓名进行学生信息的查询; 当用户…...
【爬虫开发】爬虫从0到1全知识md笔记第5篇:Selenium课程概要,selenium的其它使用方法【附代码文档】
爬虫开发从0到1全知识教程完整教程(附代码资料)主要内容讲述:爬虫课程概要,爬虫基础爬虫概述,,http协议复习。requests模块,requests模块1. requests模块介绍,2. response响应对象,3. requests模块发送请求,4. request…...

【我的代码生成器】React的FrmUser类源码
FrmUser 类的源码中:FrmUser btnSaveClick 等命名方式都是参考VB.Net的写法。 import React, { forwardRef, useImperativeHandle, useState, useEffect, } from "react"; import { makeStyles, TextField, Grid, Paper, Button, ButtonGroup, } from &q…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...