文献阅读:LESS: Selecting Influential Data for Targeted Instruction Tuning
- 文献阅读:LESS: Selecting Influential Data for Targeted Instruction Tuning
- 1. 文章简介
- 2. 方法介绍
- 1. Overview
- 2. 原理说明
- 1. SGD上的定义
- 2. Adam上的定义
- 3. 具体实现
- 1. Overview
- 1. LoRA使用
- 2. 数据选择
- 3. LESS-T
- 3. 实验考察 & 结论
- 1. 实验设计
- 2. 主要结果
- 3. 细节讨论
- 1. 计算复杂度分析
- 2. warmup是否必要
- 3. checkpoint的影响(N的影响)
- 4. LoRA Dimension的影响
- 4. 总结 & 思考
- 文献链接:https://arxiv.org/abs/2402.04333
- Github链接:https://github.com/princeton-nlp/LESS
1. 文章简介
这篇文章是陈丹琦大佬在今天二月给出的关于LLM Tuning的一篇新作。
这篇文章同样是一篇比较fundamental的基础研究工作,考察的是LLM训练,或者说任意模型训练时如何最优化的选择训练数据,从而在尽可能不损失模型性能的情况下,最优化模型训练的效率,使得模型收敛的又快又好。
相似的工作之前有主动学习相关的一系列工作,这里倒是有些区别,因为主动学习感觉还是对于未标注数据进行最优化的选取,但是这里的LESS方法感觉还是在已有的标注数据当中选取一个子集,使得模型获得足量且优秀的训练结果。
下面,我们就来看看文中给出的具体实现方法和对应的实验考察。
2. 方法介绍
1. Overview
首先,我们来看一下LESS的整体的原理说明和实现。
LESS的全程的话是Low-rank gradiEnt Similarity Search,其整体的思路的话其实还是比较直接的,就是通过数据在模型进行反向传播时产生的梯度大小来判断数据对于模型训练的影响程度,然后选择最有影响的这部分数据来进行模型finetune即可。
但是,这里会涉及到几个问题:
- 具体定义上的问题,即如何判断数据对于模型训练的影响程度大小;
- 对每一个数据都进行反向传播进行判断的话,基本也就等于跑完一个epoch了,这种效率的话就有点舍本逐末了,因此,需要考察一下如何对效率进行优化。
下面,我们就来看一下文中对于这两个问题的处理。
2. 原理说明
首先,我们来看一下文中是如何来定义一条数据对于模型训练影响的大小的。
1. SGD上的定义
首先,文中在SGD上面进行了一下简单的考察,显然,对于一步训练前后,我们可以将其在测试集上的变化一阶泰勒展开得到:
l ( z ′ ; θ t + 1 ) = l ( z ′ ; θ t ) + ⟨ ∇ l ( z ′ ; θ t ) , θ t + 1 − θ t ⟩ l(z'; \theta^{t+1}) = l(z'; \theta^{t}) + \langle \nabla l(z'; \theta^{t}), \theta^{t+1} - \theta^{t} \rangle l(z′;θt+1)=l(z′;θt)+⟨∇l(z′;θt),θt+1−θt⟩
其中,参数的改变量则有可以通过训练过程中的一轮参数迭代过程来表达,即:
θ t + 1 − θ t = − η t ∇ l ( z ; θ t ) \theta^{t+1} - \theta^{t} = -\eta_t \nabla l(z; \theta^t) θt+1−θt=−ηt∇l(z;θt)
此时,我们即可得到测试集上一轮迭代测试集上loss的变化大小可以写为:
l ( z ′ ; θ t + 1 ) − l ( z ′ ; θ t ) = − η t ⋅ ⟨ ∇ l ( z ′ ; θ t ) , ∇ l ( z ; θ t ) ⟩ l(z'; \theta^{t+1}) - l(z'; \theta^{t}) = -\eta_t \cdot \langle \nabla l(z'; \theta^{t}), \nabla l(z; \theta^t) \rangle l(z′;θt+1)−l(z′;θt)=−ηt⋅⟨∇l(z′;θt),∇l(z;θt)⟩
因此,我们就可以定义某一条训练数据对于某一条测试数据在N轮训练当中的影响程度如下:
I n f S G D ( z , z ′ ) = ∑ t = 0 N − 1 l ( z ′ ; θ t ) − l ( z ′ ; θ t + 1 ) = ∑ t = 0 N − 1 η t ⋅ ⟨ ∇ l ( z ′ ; θ t ) , ∇ l ( z ; θ t ) ⟩ \begin{aligned} \mathop{Inf}_{SGD} (z, z') &= \sum\limits_{t=0}^{N-1} l(z'; \theta^{t}) - l(z'; \theta^{t+1}) \\ &= \sum\limits_{t=0}^{N-1} \eta_t \cdot \langle \nabla l(z'; \theta^{t}), \nabla l(z; \theta^t) \rangle \end{aligned} InfSGD(z,z′)=t=0∑N−1l(z′;θt)−l(z′;θt+1)=t=0∑N−1ηt⋅⟨∇l(z′;θt),∇l(z;θt)⟩
2. Adam上的定义
但是,在我们当前的训练过程中,我们更常使用的优化器并不是SGD而是Adam,因此,文中对Adam优化器的情况进行了一下调整。
文中首先回顾了一下Adam优化器的计算:
θ t + 1 − θ t = − η t Γ ( z ; θ t ) Γ ( z ; θ t ) = m t + 1 v t + 1 + ϵ m t + 1 = β 1 m t + ( 1 − β 1 ) ∇ l ( z ; θ t ) 1 − β 1 t v t + 1 = β 2 v t + ( 1 − β 2 ) ∇ l ( z ; θ t ) 2 1 − β 2 t \theta^{t+1} - \theta^{t} = -\eta_t \Gamma (z; \theta^t) \\ \Gamma (z; \theta^t) = \frac{m^{t+1}}{\sqrt{v^{t+1} + \epsilon}} \\ m^{t+1} = \frac{\beta_1 m^t + (1-\beta_1) \nabla l(z; \theta^t)}{1-\beta_{1}^{t}} \\ v^{t+1} = \frac{\beta_2 v^t + (1-\beta_2) \nabla l(z; \theta^t)^2}{1-\beta_{2}^{t}} θt+1−θt=−ηtΓ(z;θt)Γ(z;θt)=vt+1+ϵmt+1mt+1=1−β1tβ1mt+(1−β1)∇l(z;θt)vt+1=1−β2tβ2vt+(1−β2)∇l(z;θt)2
因此,我们可以很直接地将influence的定义迁移至Adam优化器上,得到:
I n f A d a m ( z , z ′ ) = ∑ t = 0 N − 1 l ( z ′ ; θ t ) − l ( z ′ ; θ t + 1 ) = ∑ t = 0 N − 1 η t ⋅ ⟨ ∇ l ( z ′ ; θ t ) , Γ ( z ; θ t ) ⟩ \mathop{Inf}_{Adam} (z, z') = \sum\limits_{t=0}^{N-1} l(z'; \theta^{t}) - l(z'; \theta^{t+1}) = \sum\limits_{t=0}^{N-1} \eta_t \cdot \langle \nabla l(z'; \theta^{t}), \Gamma (z; \theta^t) \rangle InfAdam(z,z′)=t=0∑N−1l(z′;θt)−l(z′;θt+1)=t=0∑N−1ηt⋅⟨∇l(z′;θt),Γ(z;θt)⟩
不过实际发现模型的参数梯度与文本长度强相关:

这就导致直接迁移上述定义公式会使得数据选择明显趋于短文本,因此文中对其进行了一下修正,将其加入了一下归一化因子,最终得到定义式如下:
I n f A d a m ( z , z ′ ) = ∑ t = 0 N − 1 η t ⋅ ⟨ ∇ l ( z ′ ; θ t ) , Γ ( z ; θ t ) ⟩ ∥ ∇ l ( z ′ ; θ t ) ∥ ⋅ ∥ Γ ( z ; θ t ) ∥ \mathop{Inf}_{Adam} (z, z') = \sum\limits_{t=0}^{N-1} \eta_t \cdot \frac{\langle \nabla l(z'; \theta^{t}), \Gamma (z; \theta^t) \rangle}{\lVert \nabla l(z'; \theta^{t}) \rVert \cdot \lVert \Gamma (z; \theta^t) \rVert} InfAdam(z,z′)=t=0∑N−1ηt⋅∥∇l(z′;θt)∥⋅∥Γ(z;θt)∥⟨∇l(z′;θt),Γ(z;θt)⟩
3. 具体实现
1. Overview
有了上述影响程度的定义之后,文中就可以根据上述influence的大小进行数据选择策略了,具体来说的话,就是:
- 在训练集上进行少量的tuning作为warmup,然后在验证集上计算所有训练数据当中的influence,最后挑选出影响因子最大的数据进行模型训练。
但是,如果直接使用LLM进行warmup然后进行上述定义下的influence计算时,可以想见其计算量必然极其巨大,和我们最终优化训练效率的目的显然是南辕北辙的,因此,我们必须要优化一下这里的计算效率,具体来说的话,文中就是通过引入LoRA的方法减少总的参数量,然后进行数据的选择。
因此,总的pipeline示意图如下:

下面,我们就来看看LoRA训练和数据选择的具体细节。
1. LoRA使用
首先的话,文中使用了LoRA来进行模型的finetune,这是因为模型本身的参数量太大了,常规的像是Llama这些都至少有着6B左右的参数量,更别说那些更大的模型了,使用全部参数finetune然后反向推导influence显然成本太大了,典型的舍本逐末,因此,这里使用LoRA进行模型的finetune,可以大幅减少模型的计算量。
2. 数据选择
然后,关于数据选择的部分,文中就是使用上述原理说明部分的内容进行数据选择,具体来说的话就是先使用少量训练数据进行一下warmup,然后使用少部分测试集来计算每一条数据对于模型的影响大小,然后选择出影响最大的几条数据即可。
对应的公式如下:
I n f A d a m ( z , D v a l ) = ∑ t = 0 N − 1 η t ⋅ ⟨ ∇ l ( D v a l ; θ t ) , Γ ( z ; θ t ) ⟩ ∥ ∇ l ( D v a l ; θ t ) ∥ ⋅ ∥ Γ ( z ; θ t ) ∥ \mathop{Inf}_{Adam} (z, D_{val}) = \sum\limits_{t=0}^{N-1} \eta_t \cdot \frac{\langle \nabla l(D_{val}; \theta^{t}), \Gamma (z; \theta^t) \rangle}{\lVert \nabla l(D_{val}; \theta^{t}) \rVert \cdot \lVert \Gamma (z; \theta^t) \rVert} InfAdam(z,Dval)=t=0∑N−1ηt⋅∥∇l(Dval;θt)∥⋅∥Γ(z;θt)∥⟨∇l(Dval;θt),Γ(z;θt)⟩
3. LESS-T
在上述基础上,文中进一步提出,这里的模型可以具有泛化性,也就是说,使用基于模型A选择出来的数据集 D D D同样有利于另一个模型 B B B的训练。
因此,文中给出了一个LESS-T的数据选择方法,固定使用Llama2 7B模型来进行数据选择,然后在其他模型上进行finetune。
3. 实验考察 & 结论
下面,我们来看一下文中给出的具体实验考察以及对应的结果如下。
1. 实验设计
首先,关于文中的实验设计的话,文中主要是使用MMLU, TYDIQA, BBH三个数据集的测试集,其具体信息如下:

而实验模型的话主要是Llama2 7B, 13B以及Mistral 7B三个模型,数据选择比例的话则是以5%作为标准。
然后,作为对照组的话,主要是以下几种方法:
- 随机选择
- BM25
- DSIR
- RDS
其中,BM25和DSIR都是基于词频的选择方法,RDS全称为Representationbased
Data Selection,这部分我倒是完全不知道,有兴趣的读者可以去追一下这个文献看看这具体是个啥。
2. 主要结果
下面,我们来看一下文中给出的具体实验结果。
最直接的一个实验结果显然就是在几个数据集下LESS选择的5%的数据和全量数据训练以及随机选择5%数据的效果差异:

然后,在Llama2 7B模型上,文中进一步考察了不同的数据选择策略下模型finetune效果的差异:

基于上述两张表格,文中总结了以下几个主要的实验结论:
- 从表2可以看到,LESS在不同模型上都有效,方法具有稳定性
- 同样从表2可以看到,使用LESS方法有时选择5%的优质数据的训练效果甚至可以超过全量数据finetune的效果;
- 同样从表2可以看到,LESS-T方法在Llama2 13B和Mistral 7B模型上同样有效,说明了LESS数据选择对于模型的泛化性
- 从表3可以看到,相较于其他对照组中的方法,LESS 是唯一一个在各个任务下均有效的数据选择策略。
3. 细节讨论
此外,文中还更进一步地做了一些关于LESS的细节讨论。
1. 计算复杂度分析
首先,文中分析了一下LESS方法的整体复杂度,得到结果如下:

可以看到,LESS的计算量其实还是非常大的。
2. warmup是否必要
然后,文中考察了一下对LoRA的warmup是否必要,得到结果如下:

可以看到,warmup还是非常必要的。
3. checkpoint的影响(N的影响)
此外,关于文中使用多个checkpoint进行梯度的avg这一点,文中同样说明了一下这个操作的必要性:

4. LoRA Dimension的影响
最后,文中还考察了一下LoRA模型当中维度对于数据选择的影响:

可以看到,确实维度越大数据选择效果越好,但是小维度的下已经足以选择出很好的数据带来明显的效果提升了。
4. 总结 & 思考
综上就是陈丹琦大佬提出的LESS方法了,可以看到,在数据选择方面LESS确实给出了非常强大的效果,可以在5%左右的数据上就获得非常优秀的效果,而且数据的选择对模型还有任务都有着足够的泛化性。
但是比较困惑我的一点在于LESS的数据选择计算开销实在是非常大,而且是对于已有的训练数据进行二次提纯选择,而现实中我们的问题其实个人感觉还是更多的像是主动学习那样缺少训练数据因此要对未标注数据进行选择标注,这个问题LESS似乎是无法处理的,当然LESS也不是研究的这个问题就是了。
因此个人感觉LESS的定位就多少有些尴尬了,已有足量训练数据的情况下如此大开销地精炼数据是否真的有足够的价值,多少还是有些怀疑。
不过考虑到之前像是Meta在LIMA这篇工作中提到的那样:只需要少量的优质数据,模型就足以finetune获得非常优秀的效果了。
因此,数据质量的价值可能远高于单纯的数据量的价值,数据精炼的意义可能真的会比想象的更大吧,谁知道呢。
相关文章:

文献阅读:LESS: Selecting Influential Data for Targeted Instruction Tuning
文献阅读:LESS: Selecting Influential Data for Targeted Instruction Tuning 1. 文章简介2. 方法介绍 1. Overview2. 原理说明 1. SGD上的定义2. Adam上的定义 3. 具体实现 1. Overview1. LoRA使用2. 数据选择3. LESS-T 3. 实验考察 & 结论 1. 实验设计2. 主…...

应对中年危机-高效学习
兴致勃勃的打开一本书,从第一行,第一个字开始,十分钟later……两眼皮一塌,哎,想睡觉了,真助眠。但其实我并不懒啊。 过去我是上诉这样,现在有了改善。如果你也是这样,希望看完了本文…...

Java二叉树(2)
一、二叉树的链式存储 二叉树的存储分为顺序存储和链式存储 (本文主要讲解链式存储) 二叉树的链式存储是通过一个一个节点引用起来的,常见的表示方式有二叉三叉 // 孩子表示法 class Node { int val; // 数据域 Node left; // 左孩子的引用…...

关于AG32 MCU的一些奇思妙想
1、AG32VF103的网口是100M还是10M? RE: 都是100M的。 2、用FPGA能不能再仿出一个网口?有些产品用到两个网口。 理论上可以,但是要考虑,一个是cpld实现难度,一个是需要的逻辑单元。因为mac逻辑多,内置的2KL…...

除了sql外还有那些查询语言
除了SQL(结构化查询语言)外,还有许多其他的查询语言,包括但不限于XQuery(对XML的查询语言)、MDX(多维查询语言,用于分析数据仓库)、DQL(数据查询语言…...
构建第一个ArkTS用的资源分类与访问
应用开发过程中,经常需要用到颜色、字体、间距、图片等资源,在不同的设备或配置中,这些资源的值可能不同。 应用资源:借助资源文件能力,开发者在应用中自定义资源,自行管理这些资源在不同的设备或配置中的表…...

JVM中都有哪些引用类型
● 强引用:JVM中默认引用关系就是强引用,即是对象被局部变量、静态变量等GC Root关联的对象引用,只要这层关系存在,普通对象就不会被回收 ● 软引用:软引用相对于强引用是一种比较弱的引用关系,如果一个对象…...

分布式锁-Redission快速入门
实战篇Redis 5、分布式锁-redission 5.2 分布式锁-Redission快速入门 引入依赖: <dependency><groupId>org.redisson</groupId><artifactId>redisson</artifactId><version>3.13.6</version> </dependency>配置…...

IDEA 本地库引入了依赖但编译时找不到
在使用 IDEA 开发 Maven 项目的过程中,有时会遇到本地库引入了依赖,但编译时报找不到这个依赖,可以使用命令处理。 打开 Terminal。 执行清理命令。 mvn clean install -Dmaven.test.skiptrue执行更新命令。 mvn -U idea:idea...

hadoop最新详细版安装教程 2024 最新版
文章目录 hadoop安装教程 2024最新版提前准备工作用户配置安装 SSH Server免密登录设置编辑 SSH server 配置文件配置Java环境查看java 版本验证 环境变量设置安装Hadoop下载hadoop解压hadoop查看hadoop 版本hadoop 配置编辑编辑配置文件core-site.xml编辑配置文件hdfs-site.xm…...

Unity 中画线
前言: 在Unity项目中,调试和可视化是开发过程中不可或缺的部分。其中,绘制线条是一种常见的手段,可以用于在Scene场景和Game视图中进行调试和展示。本篇博客将为你介绍多种不同的绘制线条方法,帮助你轻松应对各种调试…...
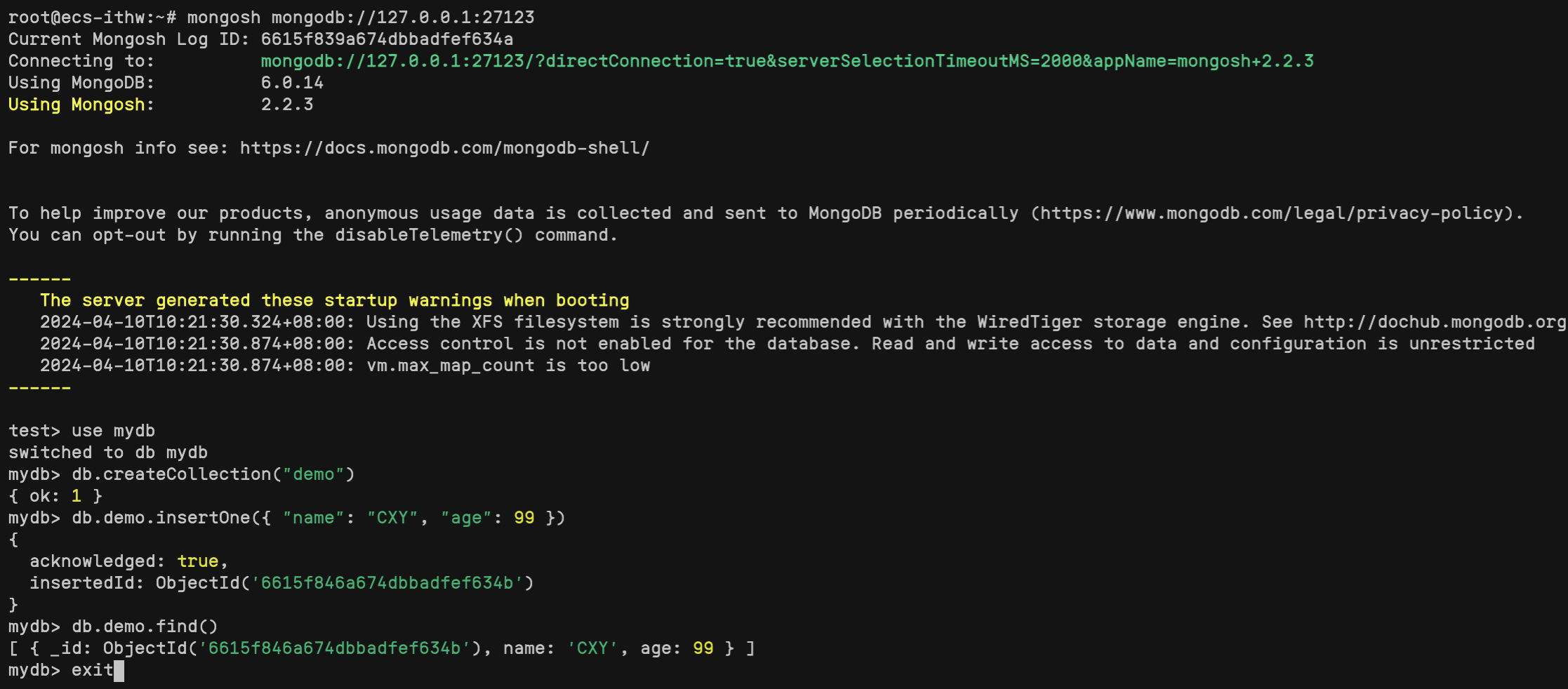
【快捷部署】017_MongoDB(6.0.14)
📣【快捷部署系列】017期信息 编号选型版本操作系统部署形式部署模式复检时间017MongoDB6.0.14Ubuntu 20.04apt单机2024-04-11 一、快捷部署 #!/bin/bash ################################################################################# # 作者:…...

Android中的Zygote进程介绍
在Android系统中,Zygote是一个特殊的进程,主要负责孵化(fork)新的应用进程,从而加速应用的启动过程。Zygote进程是系统启动过程中创建的第一个进程,它会在系统启动时被初始化并一直运行在后台。 以下是Zyg…...

世界需要和平--中介者模式
1.1 世界需要和平 "你想呀,国与国之间的关系,就类似于不同的对象与对象之间的关系,这就要求对象之间需要知道其他所有对象,尽管将一个系统分割成许多对象通常可以增加其可复用性,但是对象间相互连接的激增又会降低…...

PHPStudy(小皮)切换PHP版本PDO拓展失效的问题
因为要看一个老项目,PHP版本在8.0以上会报错,只能切换到7.2,但又遇到了PDO没开启的问题。 PHPStudy上安装的PHP7.2是需要自己配置一下的,里面php.ini文件是空的,需要将php.ini-development改成php.ini,对于…...
Golang 基于共享变量的并发锁
一、互斥锁 先看一个并发情况,同时操作一个全局变量,如果没有锁会怎么样 假设有1000个goroutines并发进行银行余额的扣除,每次都扣除10元,起始的总余额是10000,理论上并发执行完应该是0对不对,但实际却不…...
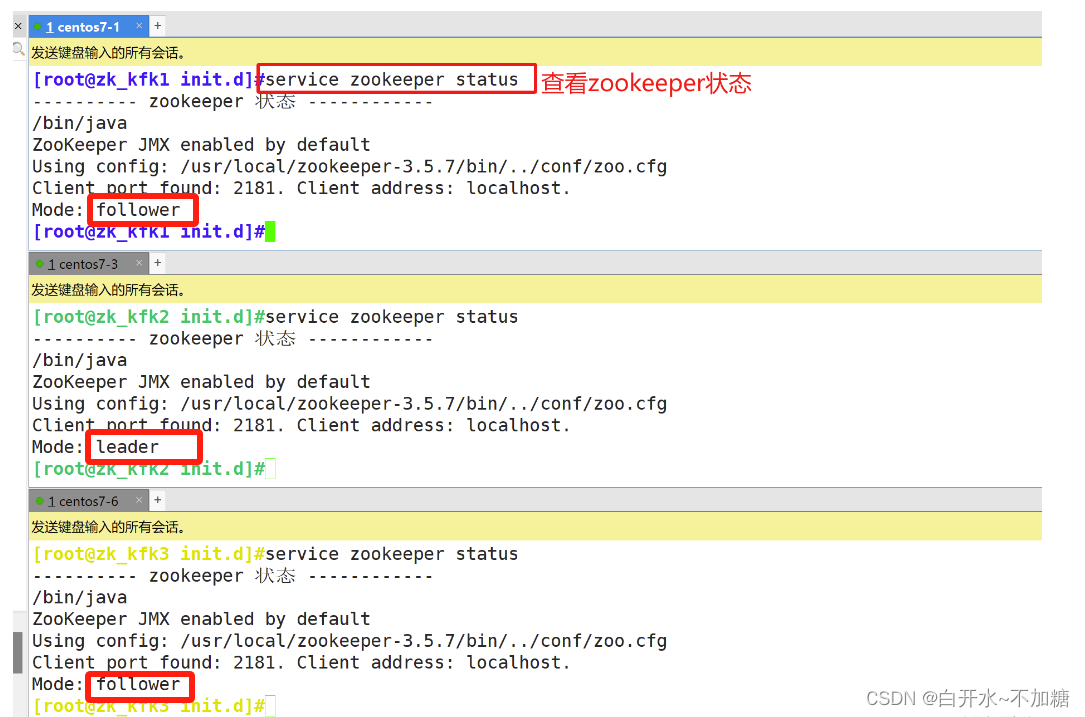
探索分布式技术--------------注册中心zookeeper
目录 一、ZooKeeper是什么 二、ZooKeeper的工作机制 三、ZooKeeper特点 四、ZooKeeper数据结构 五、ZooKeeper应用场景 5.1统一命名服务 5.2统一配置管理 5.3统一集群管理 5.4服务器动态上下线 5.5软负载均衡 六、ZooKeeper的选举机制 6.1第一次启动选举机制 6.2非…...
剑指offer之牛客与力扣——前者分类题单中的题目在后者的链接
搜索 [4.12完成] JZ1 LCR 172. 统计目标成绩的出现次数 JZ3 153. 寻找旋转排序数组中的最小值 JZ4 LCR 014. 字符串的排列 JZ5 LCR 163. 找到第 k 位数字 400 动态规划 [4.15完成] JZ2 LCR 161. 连续天数的最高销售额 53 JZ3 LCR 127. 跳跃训练 70 JZ4 LCR 126. 斐波那契…...

C# WinForm —— 05 控件简介
简介 窗体中用于输入或操作的对象,有自己的属性、方法、事件 属性:外观方法:功能事件:行为控制特征 可视化,与用户进行交互,属性,方法,事件,可供开发人员使用࿰…...
JavaEE实验三:3.5学生信息查询系统(动态Sql)
题目要求: 使用动态SQL进行条件查询、更新以及复杂查询操作。本实验要求利用本章所学知识完成一个学生信息系统,该系统要求实现3个以下功能: 1、多条件查询: 当用户输入的学生姓名不为空,则根据学生姓名进行学生信息的查询; 当用户…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
