【python】在pycharm创建一个新的项目
相关文章:
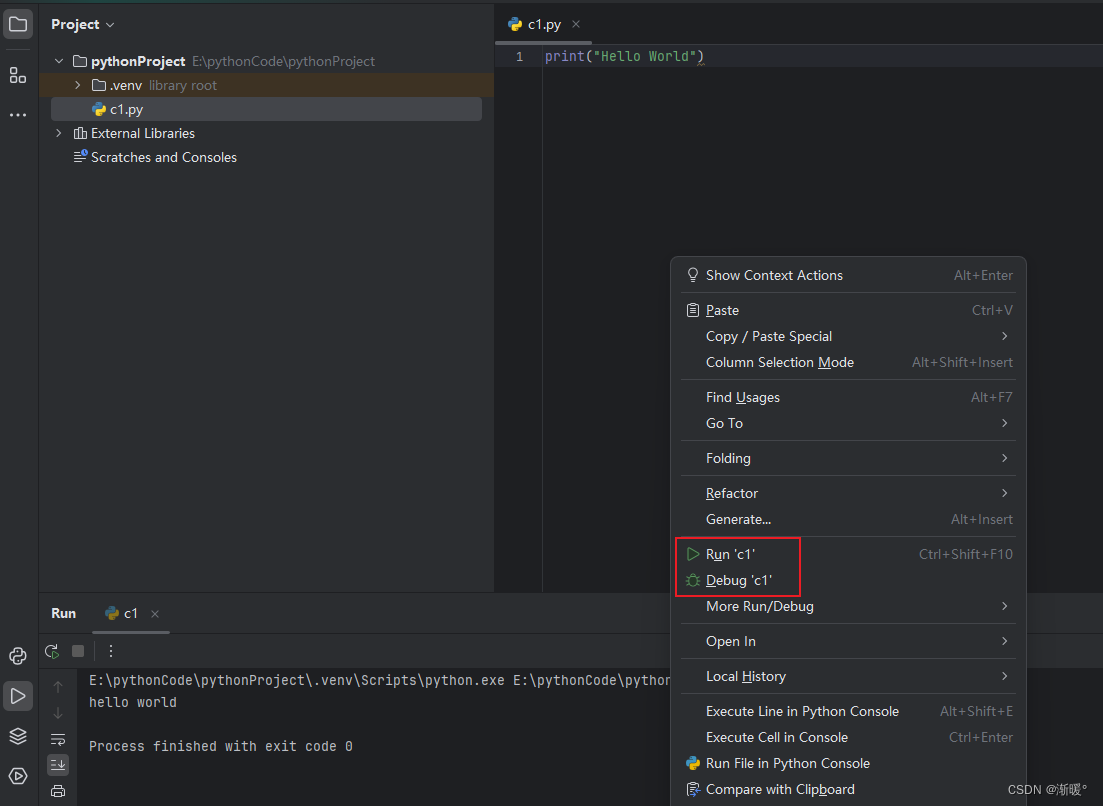
【python】在pycharm创建一个新的项目
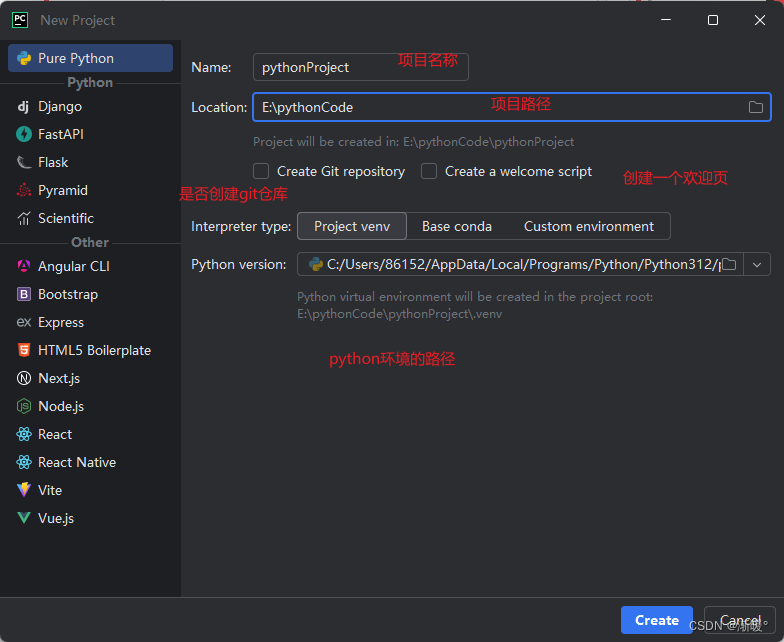
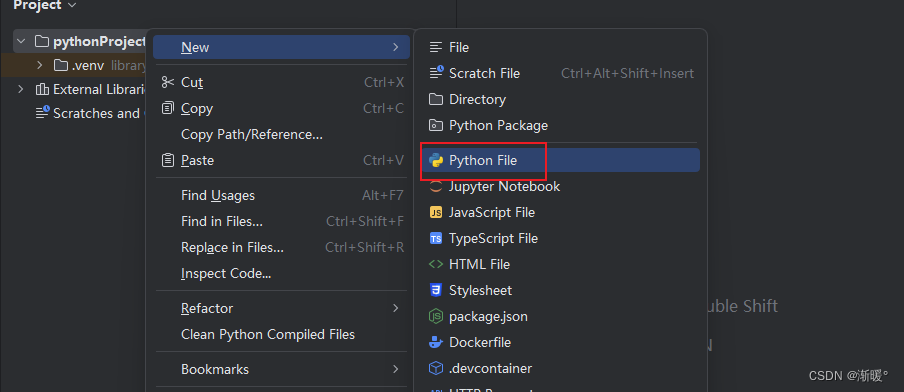
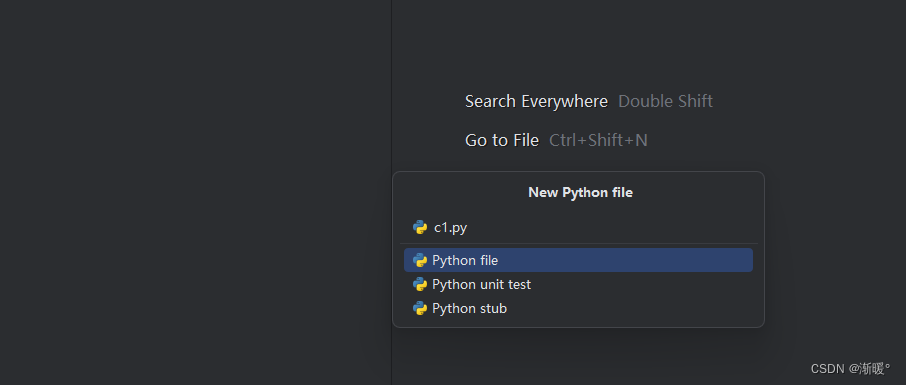
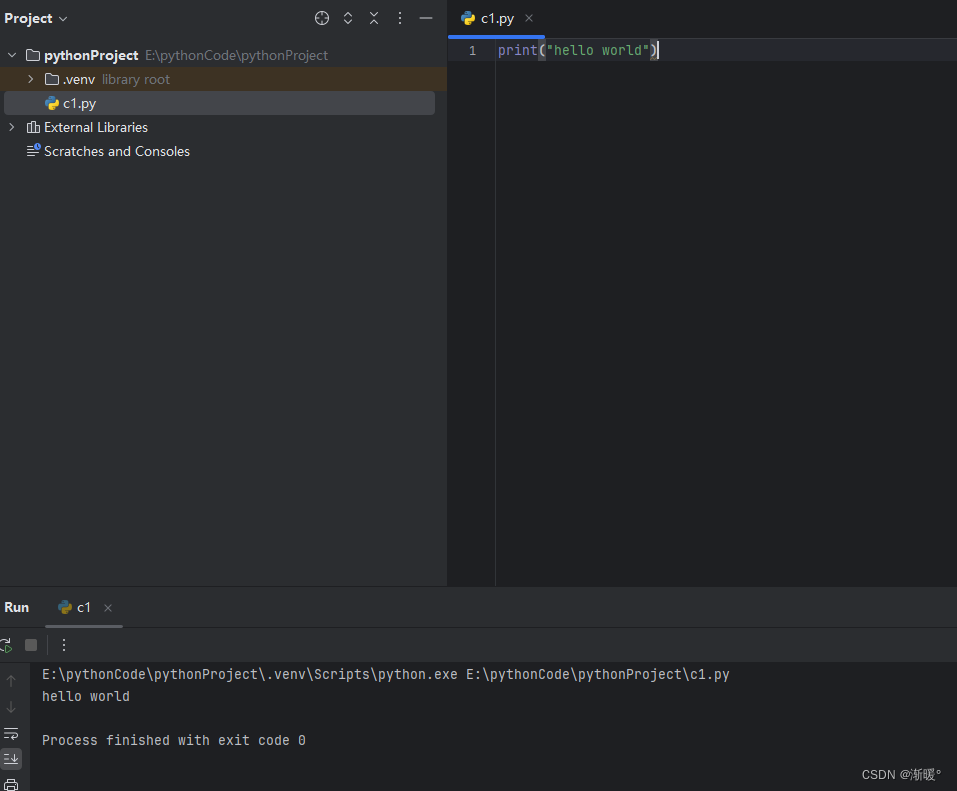
双击打开pycharm,选择create new project 选择create,后进入项目 右键项目根目录,选择new一个新的python file 随意命名一下 输入p 然后后面就会出现智能补全提示,此时轻敲一下tab,代码就写好了,非常的方便 右键执行一下代码,下面两个直接运行和debug运行都是可以的 小结 …...
----用函数实现斐波那契数列(第二遍))
java小作业(9)----用函数实现斐波那契数列(第二遍)
代码: public class Main {public static void main(String[] args) {int n 20; // 你可以更改这个值来计算和输出前n个斐波那契数for (int i 0; i < n; i) {System.out.print(fibonacci(i) " ");}}public static int fibonacci(int n) {if (n <…...
部署项目的时候的一些错误
项目打jar包,找不到资源,连接不上数据库 项目打包后无法运行 直接在idea运行可以 解决方法:pom文件中增加(配置文件如果是yml,写yml) <resources><resource><directory>src/main/java&…...
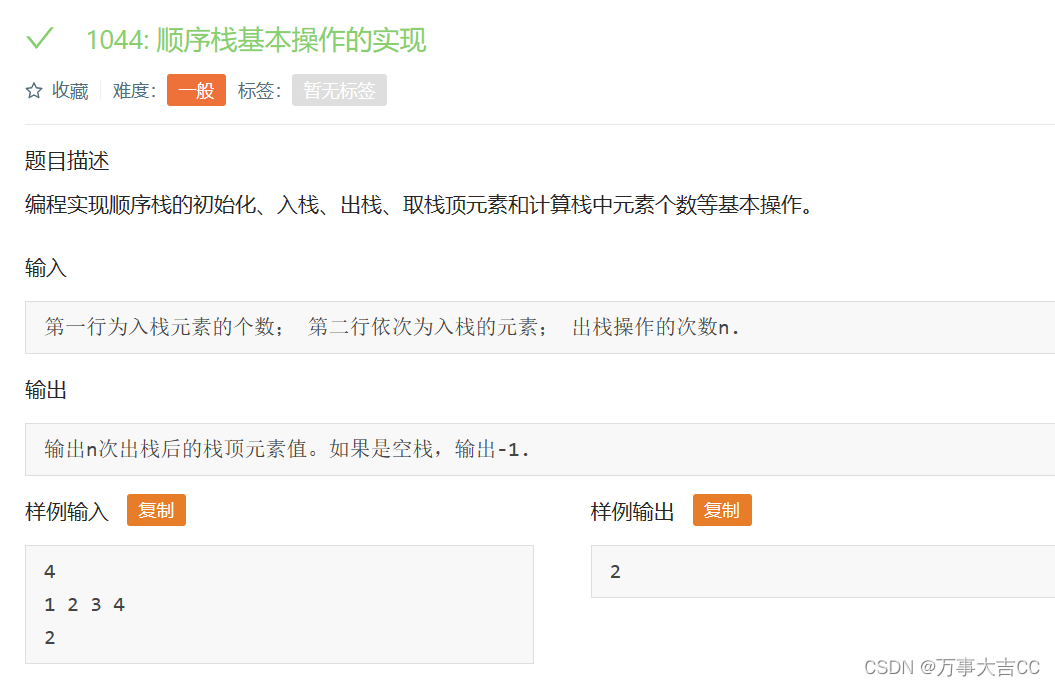
1044: 顺序栈基本操作的实现
解法: #include<iostream> #include<stack> using namespace std; int main() {int n, a, k;stack<int> sk;cin >> n;while (n--) {cin >> a;sk.push(a);}cin >> k;while (k--) {sk.pop();}if (!sk.empty()) {cout << s…...
)
微信小程序(总结)
1、wx.createSelectorQuery 在微信小程序中,wx.createSelectorQuery 是用于创建一个 SelectorQuery 对象的方法,而 this.createSelectorQuery 是在组件中获取元素的方法。 使用 wx.createSelectorQuery 创建的 SelectorQuery 对象可以用于获取页面中的…...
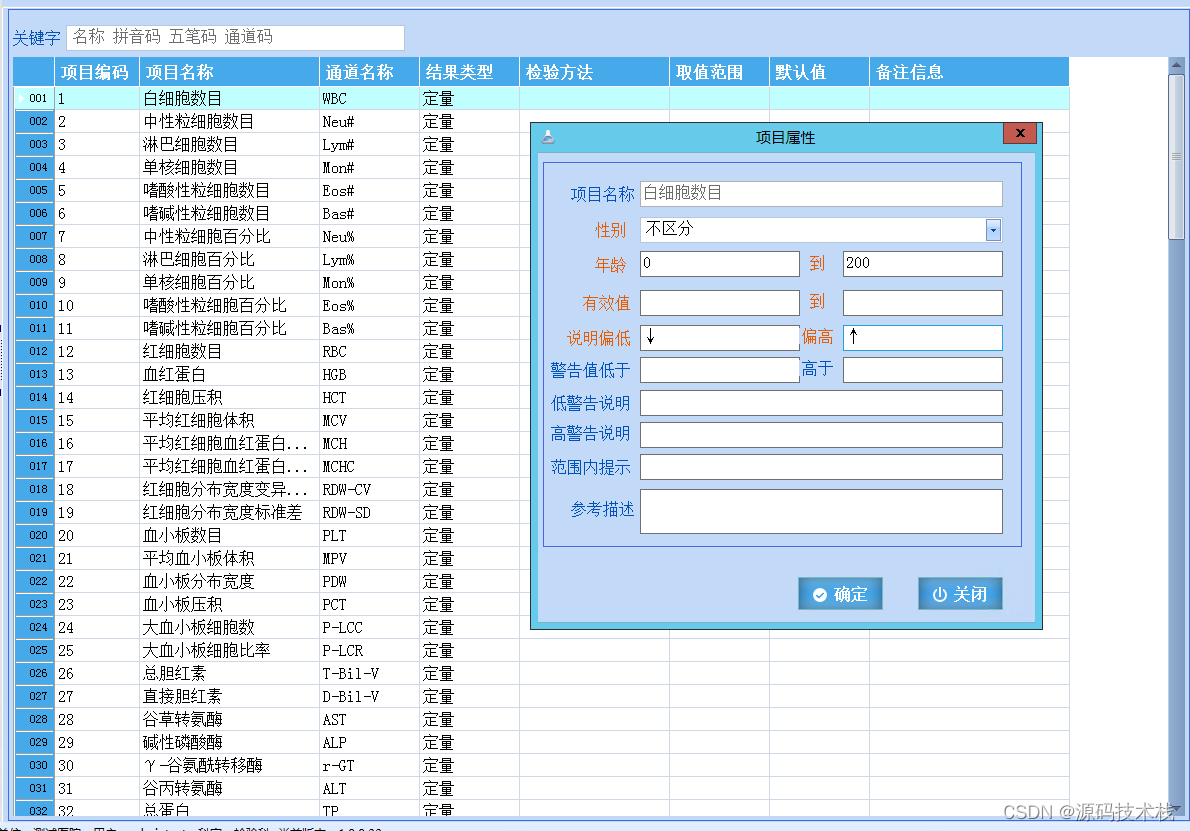
C#医学实验室/检验信息管理系统(LIS系统)源码
目录 检验系统的总体目标 LIS主要包括以下功能: LIS是集:申请、采样、核收、计费、检验、审核、发布、质控、耗材控制等检验科工作为一体的信息管理系统。LIS系统不仅是自动接收检验数据,打印检验报告,系统保存检验信息的工具&a…...

Linux驱动编程-module_platform_driver注册platform_driver
使用platform总线驱动模式编写Linux驱动时,需要注册platform_driver(用于跟.dts文件的platform_device匹配)。下面介绍2种常用注册platform_driver方法: 1、module_init()、module_exit() /* 定义平台drv,通过.name来…...
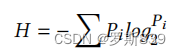
论文解读 --- 《针对PowerShell脚本的有效轻量级去混淆和语义感知攻击检测》
开篇 今天我们继续来解读安全行业优秀论文,通过学习他人的智慧成果,可以不断丰富我们的安全视野,使用它山之石来破解自身的难题。 这次要解读的论文为《Effective and Light-Weight Deobfuscation and Semantic-Aware Attack Detection for…...

在Spring Boot实战中碰到的拦截器与过滤器是什么?
在Spring Boot实战中,拦截器(Interceptors)和过滤器(Filters)是两个常用的概念,它们用于在应用程序中实现一些通用的逻辑,如日志记录、权限验证、请求参数处理等。虽然它们都可以用于对请求进行…...

数据可视化基础与应用-04-seaborn库人口普查分析--如何做人口年龄层结构金字塔
总结 本系列是数据可视化基础与应用的第04篇seaborn,是seaborn从入门到精通系列第3篇。本系列主要介绍基于seaborn实现数据可视化。 参考 参考:我分享了一个项目给你《seaborn篇人口普查分析–如何做人口年龄层结构金字塔》,快来看看吧 数据集地址 h…...

软考之【系统架构设计师】
系统架构设计师 根据原人事部、原信息产业部文件(国人部发[2003]39号)文件规定,计算机软件资格考试纳入全国专业技术人员职业资格证书制度的统一规划,实行统一大纲、统一试题、统一标准、统一证书的考试办法,每年举行…...

LigaAI x 极狐GitLab,共探 AI 时代研发提效新范式
近日,LigaAI 和极狐GitLab 宣布合作,双方将一起探索 AI 时代的研发效能新范式,提供 AI 赋能的一站式研发效能解决方案,让 AI 成为中国程序员和企业发展的新质生产力。 软件研发是一个涉及人员多、流程多、系统多的复杂工程&#…...

如何看待2023年图灵奖
目录 1.概述 2.计算复杂性理论 3.随机性和伪随机性 4.学术生涯和领导力 1.概述 图灵奖(Turing Award),全称A.M.图灵奖(ACM A.M Turing Award),是由计算机领域的最高学术机构——美国计算机协会…...
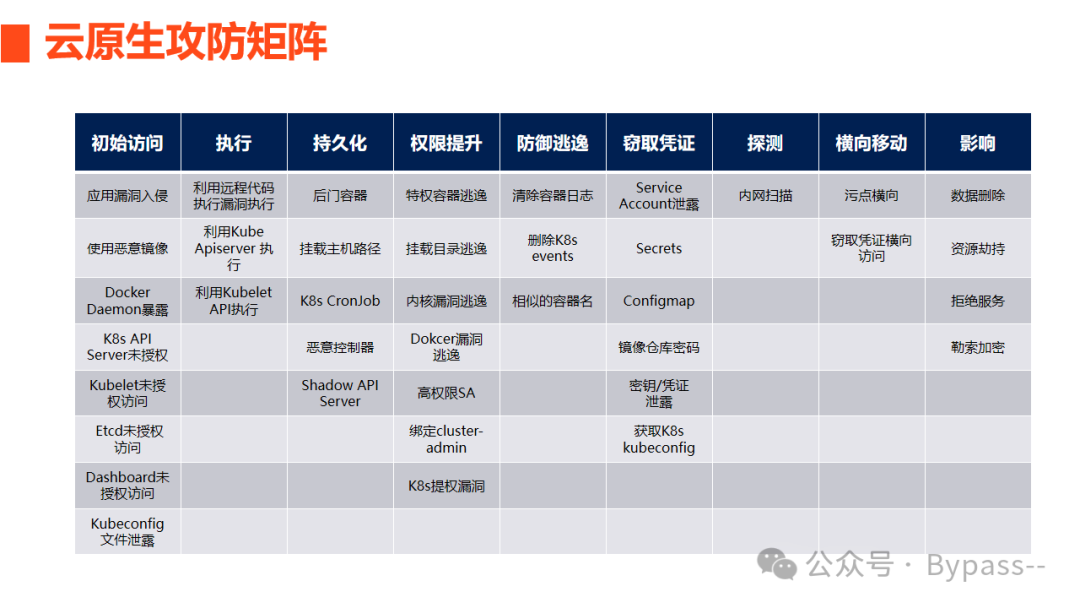
《云原生安全攻防》-- 云原生攻防矩阵
在本节课程中,我们将开始学习如何从攻击者的角度思考,一起探讨常见的容器和K8s攻击手法,包含以下两个主要内容: 云原生环境的攻击路径: 了解云原生环境的整体攻击流程。 云原生攻防矩阵: 云原生环境攻击路径的全景视图࿰…...
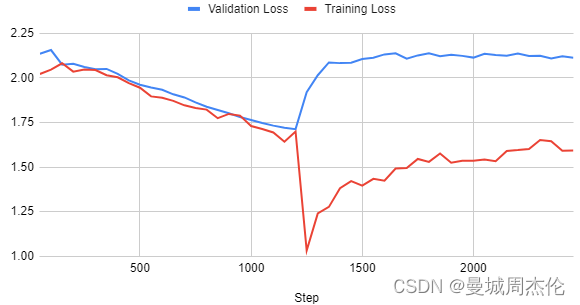
自然语言处理: 第二十七章LLM训练超参数
前言: LLM微调的超参大致有如下内容,在本文中,我们针对这些参数进行解释 training_arguments TrainingArguments(output_dir"./results",per_device_train_batch_size4,per_device_eval_batch_size4,gradient_accumulation_steps2,optim"adamw_8bi…...
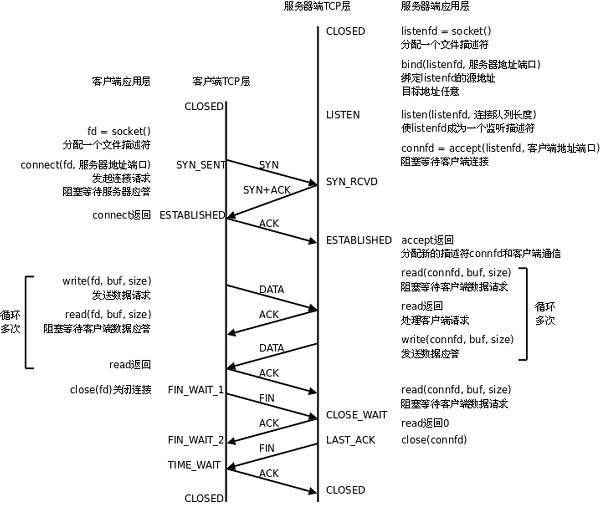
Linux使用C语言实现Socket编程
Socket编程 这一个课程的笔记 相关文章 协议 Socket编程 高并发服务器实现 线程池 网络套接字 socket: (电源)插座(电器上的)插口,插孔,管座 在通信过程中, 套接字是成对存在的, 一个客户端的套接字, 一个…...
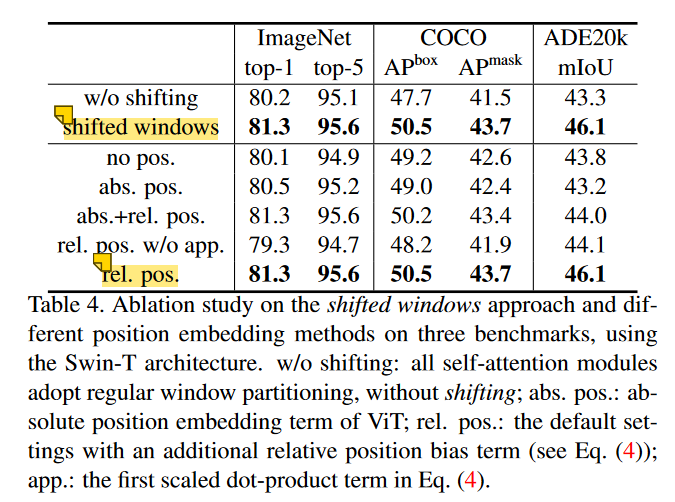
Swin Transformer——披着CNN外皮的transformer,解决多尺度序列长问题
题目:Swin Transformer: Hierarchical Vision Transformer using Shifted Windows 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》作为2021 ICCV最佳论文,屠榜了各大CV任务,性能优于DeiT、ViT和EfficientNet…...
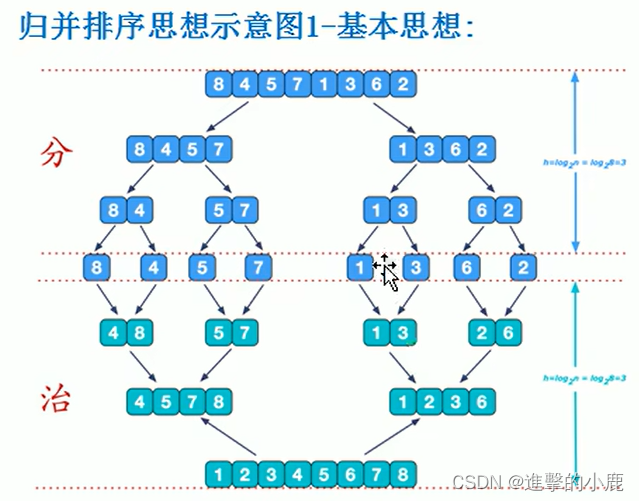
数据结构排序算法
排序也称排序算法(SortAlgorithm),排序是将一组数据,依指定的顺序进行排列的过程。 分类 内部排序【使用内存】 指将需要处理的所有数据都加载到内部存储器中进行排序插入排序 直接插入排序希尔排序 选择排序 简单选择排序堆排序 交换排序 冒泡排序快速…...

【深度剖析】曾经让人无法理解的事件循环,前端学习路线
先自我介绍一下,小编浙江大学毕业,去过华为、字节跳动等大厂,目前阿里P7 深知大多数程序员,想要提升技能,往往是自己摸索成长,但自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞…...
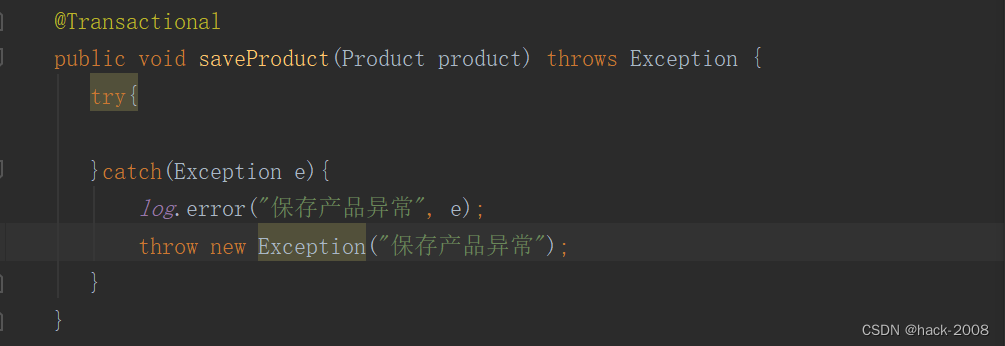
Spring 事务失效总结
前言 在使用spring过程中事务是被经常用的,如果不小心或者认识不做,事务可能会失效。下面列举几条 业务代码没有被Spring 容器管理 看下面图片类没有Componet 或者Service 注解。 方法不是public的 Transactional 注解只能用户public上,…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...