LabVIEW电信号傅里叶分解合成实验
LabVIEW电信号傅里叶分解合成实验
电信号的分析与处理在科研和工业领域中起着越来越重要的作用。系统以LabVIEW软件为基础,开发了一个集电信号的傅里叶分解、合成、频率响应及频谱分析功能于一体的虚拟仿真实验系统。系统不仅能够模拟实际电路实验箱的全部功能,还加入了实验箱不具备的频率响应、频谱分析及改变电感进行傅里叶分解等高级功能,有效提升了电路实验教学质量。
中国的集成电路产业正在快速发展,对电子信息类专业人才的需求日益增长。在此背景下,周期电信号的傅里叶分解合成实验逐渐成为理工科专业学生的一门重要实验课程。目前,高校中普遍采用的实验仪器因其电子元件数量和型号不易调节,导致实验教学效果不佳。为了克服这些局限性,利用LabVIEW开发了一套虚拟仿真实验平台,其图形用户界面让学生可以调节信号类型、幅度、频率和电路参数,极大地丰富了教学内容,提高了学生的学习效率和创新能力。
系统采用LabVIEW软件开发,特点在于其图形化编程语言,生成的独立可执行程序可以发布到校园网上,供学生随时随地下载使用。系统设计考虑到了实验的直观性和灵活性,包括周期电信号的傅里叶分解与合成、RLC串联谐振电路的选频电路模块、高通滤波器模块等多个功能模块,全面覆盖了电信号处理的基本理论和实验操作。
系统基于傅里叶级数和周期电信号的分解与合成理论,通过RLC串联谐振电路对周期信号进行频谱分析,以及利用RC无源滤波器进行高通和低通滤波实验,实现了从时域到频域的转换,有效地模拟了实际电路的行为和特性。系统的软件架构设计合理,运用了LabVIEW的多面板结构按钮操控,提供了丰富的交互界面和直观的实验效果展示。
系统或硬件的指标包括对电路参数的精确控制、实时的数据采集和处理能力、以及良好的用户交互体验。软件部分的LabVIEW编程实现了与硬件参数的动态调整和实验数据的实时反馈,确保了实验结果的准确性和重复性。
虚拟仿真实验系统以LabVIEW为平台,实现了电信号处理实验的模拟和分析,提高了教学质量和学生的学习效率。它减少了对传统硬件的依赖,使得电子技术实验教学更加现代化,为教学和科研提供了强大的工具。
相关文章:

LabVIEW电信号傅里叶分解合成实验
LabVIEW电信号傅里叶分解合成实验 电信号的分析与处理在科研和工业领域中起着越来越重要的作用。系统以LabVIEW软件为基础,开发了一个集电信号的傅里叶分解、合成、频率响应及频谱分析功能于一体的虚拟仿真实验系统。系统不仅能够模拟实际电路实验箱的全部功能&…...

Docker 学习笔记(六):挑战容器数据卷技术一文通,实战多个 MySQL 数据同步,能懂会用,初学必备
一、前言 记录时间 [2024-4-11] 系列文章简摘: Docker学习笔记(二):在Linux中部署Docker(Centos7下安装docker、环境配置,以及镜像简单使用) Docker 学习笔记(三)&#x…...

csdn怎么变得这么恶心,自动把一些好的文章分享改成了vip可见
刚刚发现以前发的一些文章未经过我同意,被csdn自动改成了VIP可见,这也太恶心了,第一你没分钱给我,第二我记录下一些问题也不是为了赚钱,而是为了提升自己和帮助别人,这样搞是想逼更多人走是吗?...

自然语言处理NLP:文本预处理Text Pre-Processing
大家好,自然语言处理(NLP)是计算机科学领域与人工智能领域中的一个重要方向,其研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。本文将介绍文本预处理的本质、原理、应用等内容,助力自然语言处理和模型的生成使用。 1.文本…...
家庭网络防御系统搭建-虚拟机安装siem/securityonion网络连接问题汇总
由于我是在虚拟机中安装的security onion,在此过程中,遇到很多的网络访问不通的问题,通过该文章把网络连接问题做一下梳理。如果直接把securityonion 安装在物理机上,网络问题则会少很多。 NAT无法访问虚拟机 security onion虚拟…...
2024年外贸行业营销神器推荐
2024年外贸行业营销神器推荐:外贸人每天面对的不是国内客户,而是全球客户,相对于国内来说,会更加麻烦和繁琐,今天就码一篇2024年外贸行业营销神器的推荐文章,希望可以减轻各位外贸人的负担! 1、…...

k8s高可用集群部署介绍 -- 理论
部署官网参考文档 负载均衡参考 官网两种部署模式拓扑图和介绍 介绍两种高可用模式 堆叠 拓扑图如下(图片来自k8s官网): 特点:将etcd数据库作为控制平台的一员,由于etcd的共识算法,所以集群最少为3个&…...

【GDAL-Python】1-在Python中使用GDAL读写栅格文件
文章目录 1-概要2.代码实现 1-概要 提示:本教程介绍如何使用 Python 中的 GDAL 库将栅格数据读取为数组并将数组另存为GeoTiff 文件 视频地址:B站对应教程 目标: (1)读写GeoTiff影像; (2&…...

【C++】explicit关键字详解(explicit关键字是什么? 为什么需要explicit关键字? 如何使用explicit 关键字)
目录 一、前言 二、explicit关键字是什么? 三、构造函数还具有类型转换的作用 🍎单参构造函数 ✨引出 explicit 关键字 🍍多参构造函数 ✨为什么需要explicit关键字? ✨怎么使用explicit关键字? 四、总结 五…...
maven引入外部jar包
将jar包放入文件夹lib包中 pom文件 <dependency><groupId>com.jyx</groupId><artifactId>Spring-xxl</artifactId><version>1.0-SNAPSHOT</version><scope>system</scope><systemPath>${project.basedir}/lib/Spr…...

李沐37_微调——自学笔记
标注数据集很贵 网络架构 1.一般神经网络分为两块,一是特征抽取原始像素变成容易线性分割的特征,二是线性分类器来做分类 微调 1.原数据集不能直接使用,因为标号发生改变,通过微调可以仍然对我数据集做特征提取 2.pre-train源…...
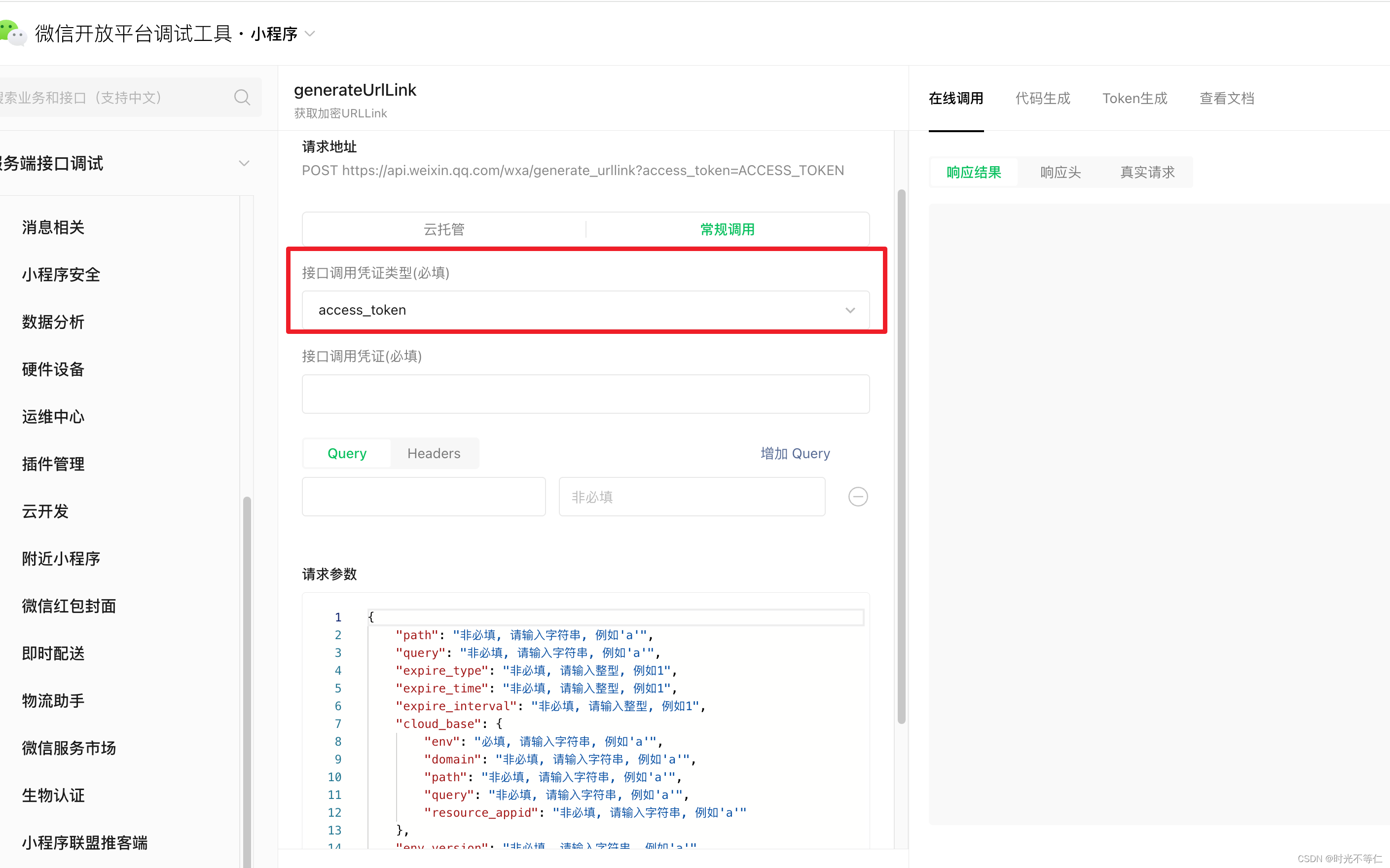
【小程序】生成短信中可点击的链接
文章目录 前言一、如何生成链接二、仔细拜读小程序开发文档文档说明1文档说明2 总结 前言 由于线上运营需求,需要给用户发送炮轰短信,用户通过短信点击链接直接跳转进入小程序 一、如何生成链接 先是找了一些三方的,生成的倒是快速…...

欧拉函数(模板题)
给定 n 个正整数 ai,请你求出每个数的欧拉函数。 欧拉函数的定义 输入格式 第一行包含整数 n。 接下来 n 行,每行包含一个正整数 ai。 输出格式 输出共 n 行,每行输出一个正整数 ai 的欧拉函数。 数据范围 1≤n≤100, 1≤ai≤2109 输…...
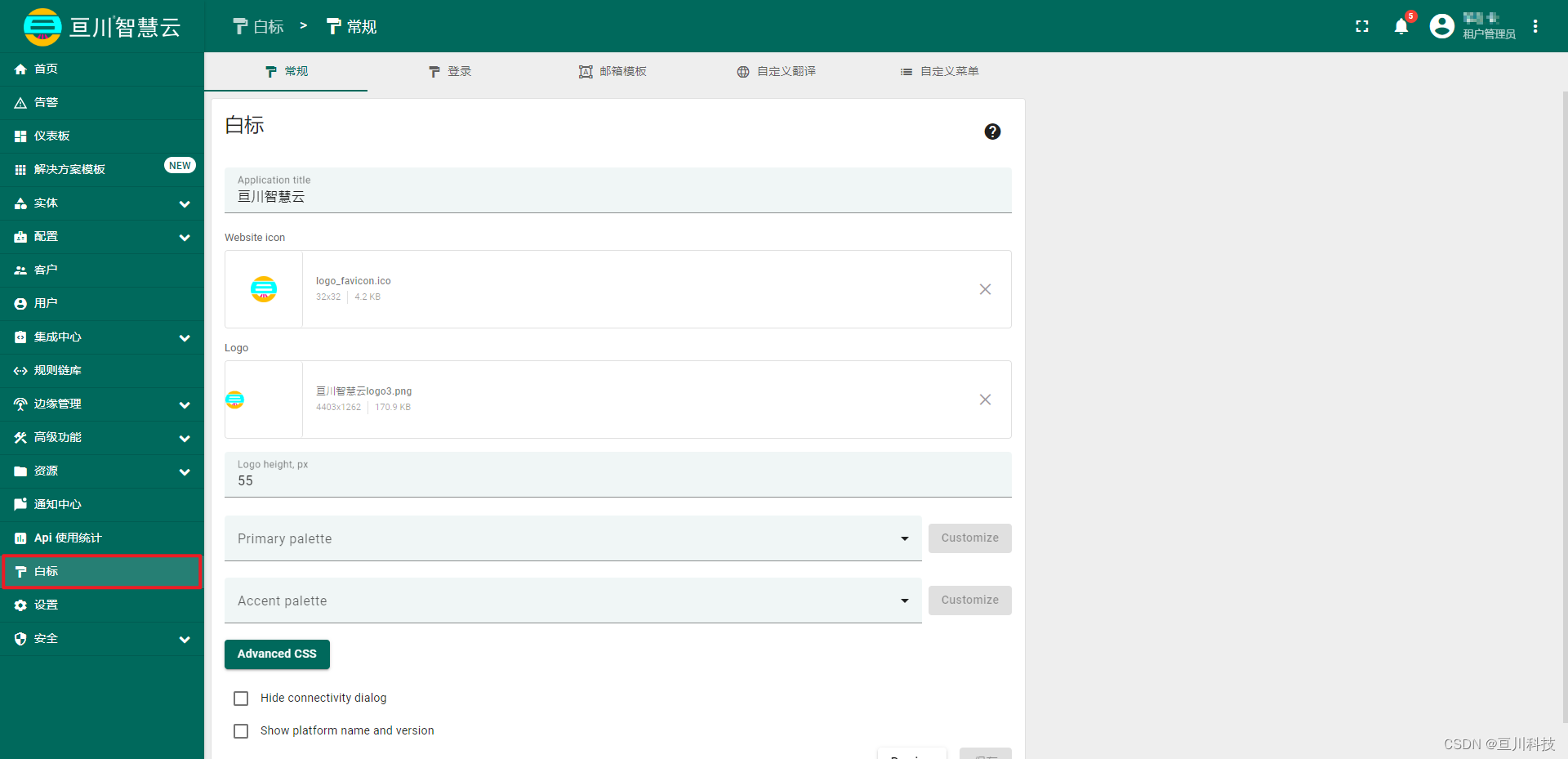
Thingsboard PE 白标的使用
只有专业版支持白标功能。 使用 ThingsBoard Cloud 或安装您自己的平台实例。 一、介绍 ThingsBoard Web 界面提供了简便的操作,让您能够轻松配置您的公司或产品标识和配色方案,无需进行编码工作或重新启动服务。 系统管理员、租户和客户管理员可以根据需要自定义配色方案、…...

智能物联网远传冷水表管理系统
智能物联网远传冷水表管理系统是一种基于物联网技术的先进系统,旨在实现对冷水表的远程监测、数据传输和智能化管理。本文将从系统特点、构成以及带来的效益三个方面展开介绍。 系统特点 1.远程监测:系统可以实现对冷水表数据的远程监测,无…...
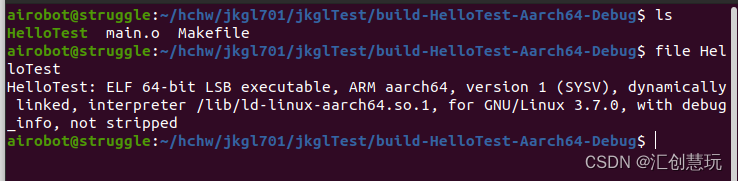
Qt教程3-Ubuntu(x86_64)上配置arm64(aarch64)交叉编译环境及QT编译arm64架构工程
汇创慧玩 写在前面1. 查看系统架构相关指令2. ARM64交叉编译器环境搭建3. Qt编译arm64环境搭建4. 配置 Qt的本地aarch64交叉编译器5. 工程建立及编译验证 写在前面 苦辣酸甜时光八载,春夏秋冬志此一生 Qt简介: Qt(官方发音 [kju:t]ÿ…...
-Python-OD统一考试(C卷))
2024年华为OD机试真题-最长子字符串的长度(二)-Python-OD统一考试(C卷)
题目描述: 给你一个字符串 s,字符串s首尾相连成一个环形 ,请你在环中找出l、o、x 字符都恰好出现了偶数次最长子字符串的长度。 输入描述: 输入是一串小写的字母组成的字符串。 输出描述: 输出是一个整数 补充说明: 1 <= s.length <= 5 x 10^5 s 只包含小写英文字母…...

【24届数字IC秋招总结】正式批面试经验汇总5——蔚来、tp-link
文章目录 一、蔚来-数字芯片验证工程师1.1 一面面试问题1.2 二面面试问题二、tp-link-数字IC验证工程师2.1 面试问题一、蔚来-数字芯片验证工程师 面试时间:9.6 10.6 1.1 一面面试问题 1、 讲下项目结构 2、 scoreboard如何进行数据对比的 3、 golden 数据怎么产生的 4、 在…...
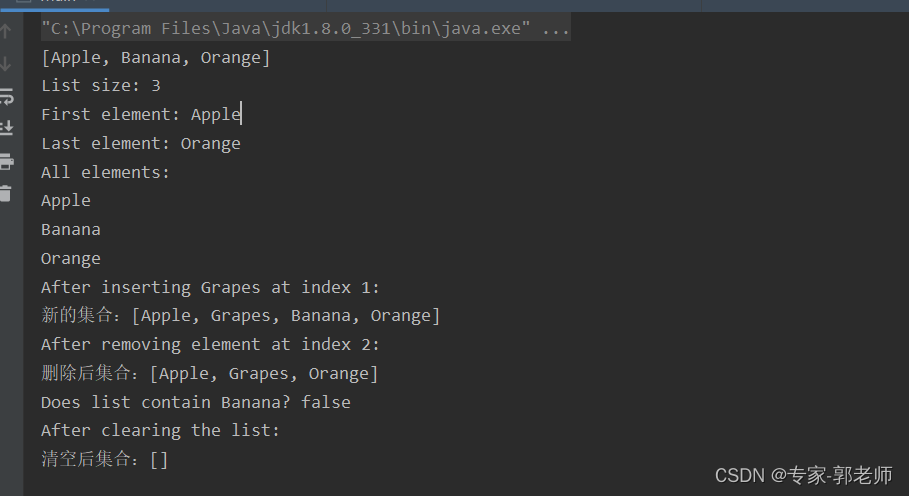
【JAVA基础篇教学】第八篇:Java中List详解说明
博主打算从0-1讲解下java基础教学,今天教学第八篇:Java中List详解说明。 在 Java 编程中,List 接口是一个非常常用的集合接口,它代表了一个有序的集合,可以包含重复的元素。List 接口提供了一系列操作方法,…...
RN向上向下滑动组件封装(带有渐变色)
这段组件代码逻辑是出事有一个View和下面的块,下面的块也就是红色区域可以按住向上向下滑动,当滑动到屏幕最上面则停止滑动,再向上滑动的过程中,上方的View的背景色也会有个渐变效果,大概逻辑就是这样 代码如下 import React, {useEffect, useRef, useState} from react; impo…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
