偏微分方程算法之混合边界差分
目录
一、研究对象
二、差分格式
2.1 向前欧拉格式
1. 中心差商
1.1.1 理论推导
1.1.2 算例实现
2. x=0处向前差商,x=1处向后差商
1.2.1 理论推导
1.2.2 算例实现
2.2 Crank-Nicolson格式
2.2.1 理论推导
2.2.2 算例实现
一、研究对象
这里我们以混合边界(导数边界)条件下的抛物型方程初边值问题:
其中,且当
同时为0时公式(1)中的边界条件是诺依曼条件。
二、差分格式
这里我们用向前欧拉法显格式和Crank-Nicolson格式进行差分格式建立。
2.1 向前欧拉格式
1. 中心差商
1.1.1 理论推导
网格剖分参照偏微分方程算法之向前欧拉法(Forward Euler)-CSDN博客。在节点处得到节点离散方程:
利用一阶向前差商代替微商,可得:
边界条件采用中心差商
其中中x变量都已经越界,属于虚拟数值,将在下文单独处理。将上面各式带入公式(2)中,将数值解代替精确解并忽略高阶项,可得到离散差分格式:
公式(3)中第1式可以写成:
其中。为处理越界问题,设公式(4)对i=0和i=1都成立,即:
将上式与公式(3)中的第3式以及、
联立,可得:
联合公式(5)、(6)可得:
1.1.2 算例实现
抛物型初边值问题:
已知精确解为,其中
是方程
的根。取
。
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int m, n, i, k;double h, tau, a,lambda,mu,r;double *x, *t,**u;double f(double x, double t);double phi(double x);double alpha(double t);double beta(double t);m=10;n=400;h=1.0/m;tau=1.0/n;a=1.0;lambda=1.0;mu=1.0;r=a*tau/(h*h);printf("r=%.4f.\n", r);x=(double *)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=i*h;t=(double *)malloc(sizeof(double)*(n+1));for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(i=0;i<=m;i++)u[i]=(double *)malloc(sizeof(double)*(n+1));for(i=0;i<=m;i++)u[i][0]=phi(x[i]);for(k=0;k<n;k++){u[0][k+1]=(1.0-2*r-2*r*lambda*h)*u[0][k]+2*r*u[1][k]-2*r*h*alpha(t[k])+tau*f(x[0], t[k]);for(i=1;i<m;i++)u[i][k+1]=r*u[i-1][k]+(1-2*r)*u[i][k]+r*u[i+1][k]+tau*f(x[i],t[k]);u[m][k+1]=2*r*u[m-1][k]+(1.0-2*r-2*r*mu*h)*u[m][k]+2*r*h*beta(t[k])+tau*f(x[m],t[k]);}printf("t/x 0 0.1 0.2 0.3 0.4 0.5\n");for(k=1;k<=8;k++){printf("%.4f ", t[k]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k]);printf("\n");}printf("\n");printf("……\n");printf("\n");printf("0.1000 ");for(i=0;i<=m/2;i++)printf("%.4f ", u[i][40]);printf("\n");for(k=1; k<=4; k=2*k){printf("%.4f ", t[k*100]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k*100]);printf("\n");}return 0;
}double f(double x, double t)
{return 0;
}
double phi(double x)
{return 1.0;
}
double alpha(double t)
{return 0.0;
}
double beta(double t)
{return 0.0;
}结果如下:
r=0.2500.
t/x 0 0.1 0.2 0.3 0.4 0.5
0.0025 0.9500 1.0000 1.0000 1.0000 1.0000 1.0000
0.0050 0.9275 0.9875 1.0000 1.0000 1.0000 1.0000
0.0075 0.9111 0.9756 0.9969 1.0000 1.0000 1.0000
0.0100 0.8978 0.9648 0.9923 0.9992 1.0000 1.0000
0.0125 0.8864 0.9549 0.9872 0.9977 0.9998 1.0000
0.0150 0.8764 0.9459 0.9818 0.9956 0.9993 0.9999
0.0175 0.8673 0.9375 0.9762 0.9931 0.9985 0.9996
0.0200 0.8590 0.9296 0.9708 0.9902 0.9974 0.9991……0.1000 0.7175 0.7829 0.8345 0.8718 0.8942 0.9017
0.2500 0.5541 0.6048 0.6452 0.6745 0.6923 0.6983
0.5000 0.3612 0.3942 0.4205 0.4396 0.4512 0.4551
1.0000 0.1534 0.1674 0.1786 0.1867 0.1917 0.19332. x=0处向前差商,x=1处向后差商
1.2.1 理论推导
利用一阶向前差商代替微商,可得:
边界条件处理如下:
将上式带入公式(2),将数值解代替精确解并忽略高阶项,可得离散格式:
整理可得:
1.2.2 算例实现
抛物型初边值问题:
已知精确解为,其中
是方程
的根。取
。
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int m, n, i, k;double h, tau, a,lambda,mu,r;double *x, *t,**u;double f(double x, double t);double phi(double x);double alpha(double t);double beta(double t);m=10;n=400;h=1.0/m;tau=1.0/n;a=1.0;lambda=1.0;mu=1.0;r=a*tau/(h*h);printf("r=%.4f.\n", r);x=(double *)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=i*h;t=(double *)malloc(sizeof(double)*(n+1));for(k=0;k<=n;k++)t[k]=k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(i=0;i<=m;i++)u[i]=(double *)malloc(sizeof(double)*(n+1));for(i=0;i<=m;i++)u[i][0]=phi(x[i]);for(k=0;k<n;k++){for(i=1;i<m;i++)u[i][k+1]=r*u[i-1][k]+(1-2*r)*u[i][k]+r*u[i+1][k]+tau*f(x[i],t[k]);u[0][k+1]=(u[1][k+1]-h*alpha(t[k]))/(1.0+lambda*h);u[m][k+1]=(u[m-1][k+1]+h*beta(t[k]))/(1.0+mu*h);}printf("t/x 0 0.1 0.2 0.3 0.4 0.5\n");for(k=1;k<=8;k++){printf("%.4f ", t[k]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k]);printf("\n");}printf("\n");printf("……\n");printf("\n");printf("0.1000 ");for(i=0;i<=m/2;i++)printf("%.4f ", u[i][40]);printf("\n");for(k=1; k<=4; k=2*k){printf("%.4f ", t[k*100]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k*100]);printf("\n");}return 0;
}double f(double x, double t)
{return 0;
}
double phi(double x)
{return 1.0;
}
double alpha(double t)
{return 0.0;
}
double beta(double t)
{return 0.0;
}结果如下:
r=0.2500.
t/x 0 0.1 0.2 0.3 0.4 0.5
0.0025 0.9091 1.0000 1.0000 1.0000 1.0000 1.0000
0.0050 0.8884 0.9773 1.0000 1.0000 1.0000 1.0000
0.0075 0.8734 0.9607 0.9943 1.0000 1.0000 1.0000
0.0100 0.8612 0.9473 0.9873 0.9986 1.0000 1.0000
0.0125 0.8507 0.9358 0.9801 0.9961 0.9996 1.0000
0.0150 0.8415 0.9256 0.9730 0.9930 0.9989 0.9998
0.0175 0.8331 0.9164 0.9662 0.9895 0.9976 0.9993
0.0200 0.8255 0.9080 0.9596 0.9857 0.9960 0.9985……0.1000 0.6901 0.7591 0.8140 0.8537 0.8778 0.8859
0.2500 0.5230 0.5753 0.6170 0.6474 0.6658 0.6720
0.5000 0.3298 0.3627 0.3890 0.4082 0.4198 0.4237
1.0000 0.1311 0.1442 0.1547 0.1623 0.1669 0.16852.2 Crank-Nicolson格式
边界条件采用中心差商。
2.2.1 理论推导
在虚拟节点处得离散方程:
利用差商代替微商:
其中同样越界,将上式代入公式(8),用数值解代替精确解并忽略高阶项,可得离散格式:
公式(9)中第1式可写为
为处理越界问题,设公式(10)对i=0和i=m都成立,即:
将上式与公式(9)中的第3式以及、
联立,可得:
联合上面两式与公式(10)可得:
上式可写出矩阵形式:
上式可用追赶法求解。
2.2.2 算例实现
抛物型初边值问题:
已知精确解为,其中
是方程
的根。取
。
代码如下:
#include<cmath>
#include<stdio.h>
#include<stdlib.h>int main(int argc, char* argv[])
{int m, n, i, k;double h, tau, a, lambda,mu,r;double *x, *t, *a1, *b, *c, *d, *ans, **u, tkmid;double f(double x, double t);double phi(double x);double alpha(double t);double beta(double t);double * chase_algorithm(double *a, double *b, double *c, double *d, int n);m=10;n=400;h=1.0/m;tau=1.0/n;a=1.0;lambda=1.0;mu=1.0;r=a*tau/(h*h);printf("r=%.4f\n", r);x=(double *)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i] = i*h;t=(double *)malloc(sizeof(double)*(n+1));for(k=0;k<=n;k++)t[k] = k*tau;u=(double **)malloc(sizeof(double *)*(m+1));for(i=0;i<=m;i++)u[i]=(double *)malloc(sizeof(double)*(n+1));for(i=0;i<=m;i++)u[i][0]=phi(x[i]);a1=(double *)malloc(sizeof(double)*(m+1));b=(double *)malloc(sizeof(double)*(m+1));c=(double *)malloc(sizeof(double)*(m+1));d=(double *)malloc(sizeof(double)*(m+1));ans=(double *)malloc(sizeof(double)*(m+1));for(k=0;k<n;k++){tkmid=(t[k]+t[k+1])/2.0;for(i=1;i<m;i++){d[i]=r*u[i-1][k]/2.0+(1.0-r)*u[i][k]+r*u[i+1][k]/2.0+tau*f(x[i],tkmid);a1[i]=-r/2.0;b[i]=1.0+r;c[i]=a1[i];}b[0]=1.0+r+r*lambda*h;b[m]=1.0+r+r*mu*h;c[0]=-r;a1[m]=-r;d[0]=(1.0-r-r*lambda*h)*u[0][k]+r*u[1][k]-r*h*alpha(t[k])-r*h*alpha(t[k+1])+tau*f(x[0],tkmid);d[m]=r*u[m-1][k]+(1.0-r-r*mu*h)*u[m][k]+r*h*beta(t[k])+r*h*beta(t[k+1])+tau*f(x[m],tkmid);ans=chase_algorithm(a1,b,c,d,m+1);for(i=0;i<=m;i++)u[i][k+1]=ans[i];}free(a1);free(b);free(c);free(d);printf("t/x 0 0.1 0.2 0.3 0.4 0.5\n");for(k=1;k<=8;k++){printf("%.4f ", t[k]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k]);printf("\n");}printf("\n");printf("……\n");printf("\n");printf("0.1000 ");for(i=0;i<=m/2;i++)printf("%.4f ", u[i][40]);printf("\n");for(k=1;k<=4;k=2*k){printf("%.4f ", t[k*100]);for(i=0;i<=m/2;i++)printf("%.4f ", u[i][k*100]);printf("\n");}return 0;
}double f(double x, double t)
{return 0;
}
double phi(double x)
{return 1.0;
}
double alpha(double t)
{return 0.0;
}
double beta(double t)
{return 0.0;
}
double * chase_algorithm(double *a, double *b, double *c, double *d, int n)
{int i;double * ans, *g, *w, p;ans=(double *)malloc(sizeof(double)*n);g=(double *)malloc(sizeof(double)*n);w=(double *)malloc(sizeof(double)*n);g[0]=d[0]/b[0];w[0]=c[0]/b[0];for(i=1;i<n;i++){p=b[i]-a[i]*w[i-1];g[i]=(d[i]-a[i]*g[i-1])/p;w[i]=c[i]/p;}ans[n-1]=g[n-1];i=n-2;do{ans[i]=g[i]-w[i]*ans[i+1];i=i-1;}while(i>=0);free(g);free(w);return ans;
}结果如下:
r=0.2500
t/x 0 0.1 0.2 0.3 0.4 0.5
0.0025 0.9600 0.9960 0.9996 1.0000 1.0000 1.0000
0.0050 0.9347 0.9868 0.9980 0.9997 1.0000 1.0000
0.0075 0.9164 0.9765 0.9950 0.9991 0.9999 1.0000
0.0100 0.9021 0.9663 0.9910 0.9980 0.9996 0.9999
0.0125 0.8900 0.9567 0.9864 0.9964 0.9992 0.9997
0.0150 0.8795 0.9478 0.9813 0.9944 0.9985 0.9993
0.0175 0.8701 0.9394 0.9762 0.9920 0.9975 0.9988
0.0200 0.8616 0.9315 0.9709 0.9893 0.9963 0.9981……0.1000 0.7180 0.7834 0.8350 0.8720 0.8943 0.9017
0.2500 0.5547 0.6054 0.6458 0.6751 0.6929 0.6989
0.5000 0.3618 0.3949 0.4213 0.4404 0.4520 0.4559
1.0000 0.1540 0.1681 0.1793 0.1874 0.1924 0.1940相关文章:
偏微分方程算法之混合边界差分
目录 一、研究对象 二、差分格式 2.1 向前欧拉格式 1. 中心差商 1.1.1 理论推导 1.1.2 算例实现 2. x0处向前差商,x1处向后差商 1.2.1 理论推导 1.2.2 算例实现 2.2 Crank-Nicolson格式 2.2.1 理论推导 2.2.2 算例实现 一、研究对象 这里我们以混合边界…...

中国八大古都,分别是哪8个?
中国历史上统一王朝或者在全局范围内看呈鼎立之势的大的政权的首都,称古都,又称都城、国都等,是古代王朝的政治中心,也是经济和文化中心。 1、西安 西安,古称长安,是中国历史上建都时间最长、建都朝代最多…...

财务信息化与财务软件有何区别与联系?
财务产品与财务信息化,两者究竟有何不同,又有何相通之处?或许,你心中也充满了这样的疑惑。那么,让我用一则小故事,为你揭晓其中的秘密。 想象这样一个场景,长尾狐狸,作为饭团公司的…...
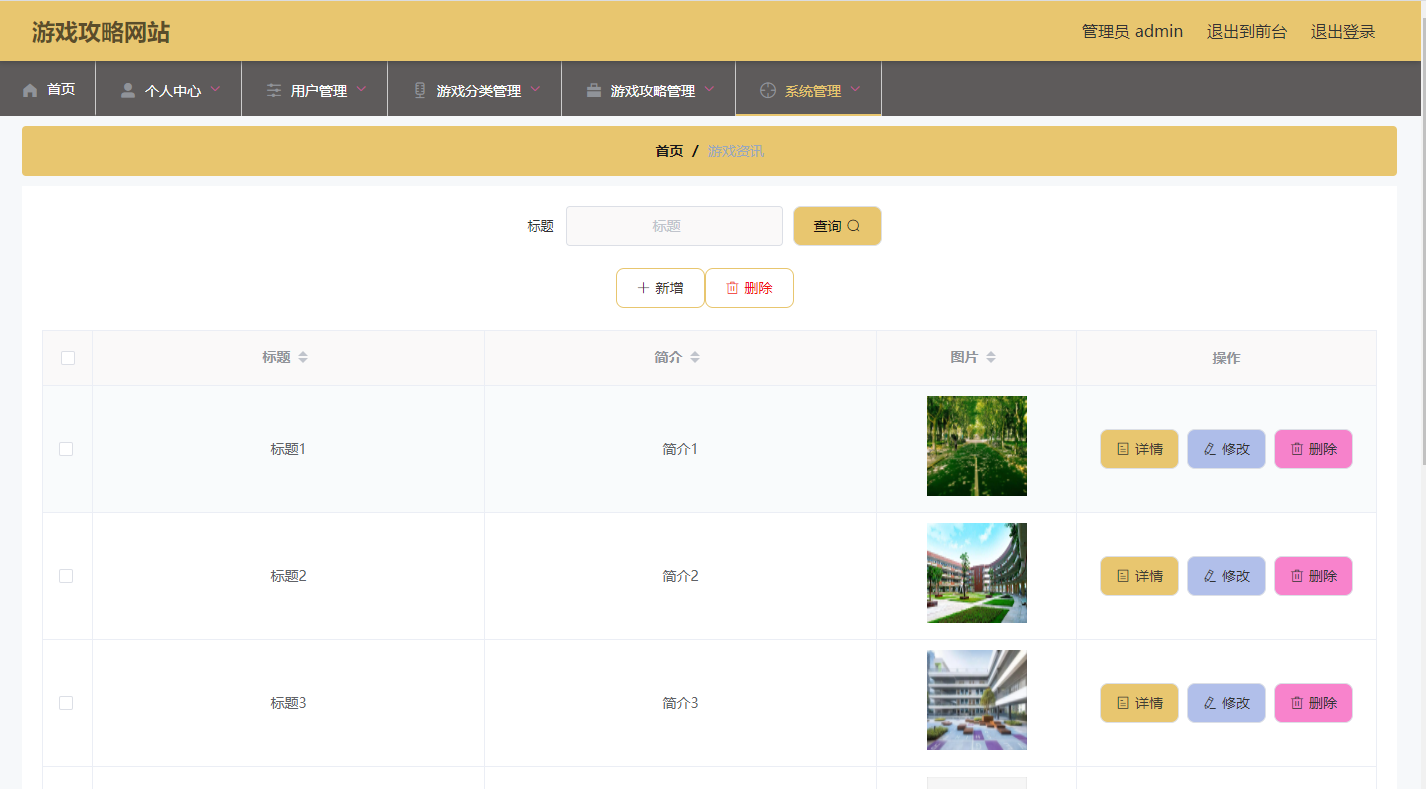
ssm052游戏攻略网站的设计与实现+vue
游戏攻略网站设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本游戏攻略网站就是在这样的大环境下诞生,其可以帮助管理者在短时间内处…...
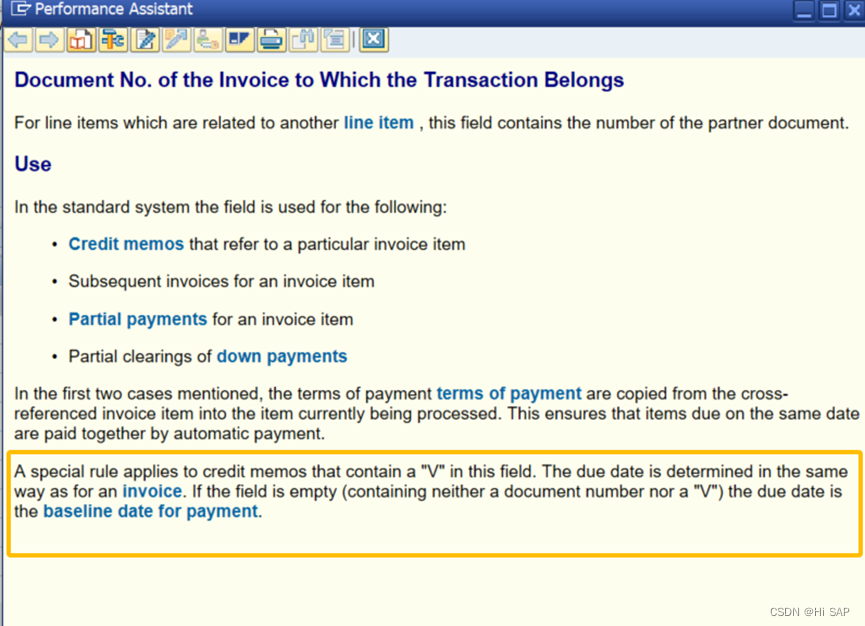
SAP Credit Memo 到期日设置技巧
当我们用FB60, MIRO或者FB70 记账vendor或者customer 的Credit Memo的时候,我们发现Credit Memo的Due Date不受付款条款的影响,默认为跟baseline date是同一天,并且无法手工更改,那么如果要设置到期日怎么操作呢? 首先…...

软件开发安全设计方案
2.1.应用系统架构安全设计要求 2.2.应用系统软件功能安全设计要求 2.3.应用系统存储安全设计要求 2.4.应用系统通讯安全设计要求 2.5.应用系统数据库安全设计要求 2.6.应用系统数据安全设计要求 软件开发全资料获取:软件开发全套资料_软件开发资料-CSDN博客https://…...

【Zabbix】zabbix 软件监控
使用zabbix监控系统查看服务器状态以及网站流量指标,利用监控系统的数据去了解上线发布的结果,和网站的健康状态 利用一个优秀的监控软件,我们可以: ●通过一个友好的界面进行浏览整个网站所有的服务器状态 ●可以在 Web 前端方便的查看监控…...

Vue Router 路由动态缓存组件
文章目录 一、简介基本用法生命周期钩子 二、定义是否缓存组件三、缓存组件1. 通过 :include 属性实现vue2.x中vue3.x中 2. 通过 v-slot 功能实现3. 通过 v-if 来实现 四、注意事项 一、简介 Vue Router 允许你缓存路由组件,这样在用户导航回之前的页面时ÿ…...

数据结构:线性表————单链表专题
🌈个人主页:小新_- 🎈个人座右铭:“成功者不是从不失败的人,而是从不放弃的人!”🎈 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 🏆所属专栏࿱…...
JMM中的内存屏障)
多线程(54)JMM中的内存屏障
Java内存模型(JMM)中的内存屏障是一种保证内存可见性、顺序性的底层机制。它们是一组指令,用于在多线程环境中确保内存操作的有序性和可见性。内存屏障主要分为四类:LoadLoad、StoreStore、LoadStore和StoreLoad。 内存屏障的类型…...

什么是流量清洗?
随着网络企业的迅速发展,越来越多的用户都开始关注关于网络流量的问题,同时,随着网络流量的增多,网络上也出现了大量的垃圾信息和恶意攻击,给网络带来了很大的困扰,而流量清洗则能够解决这个问题。 流量清洗…...
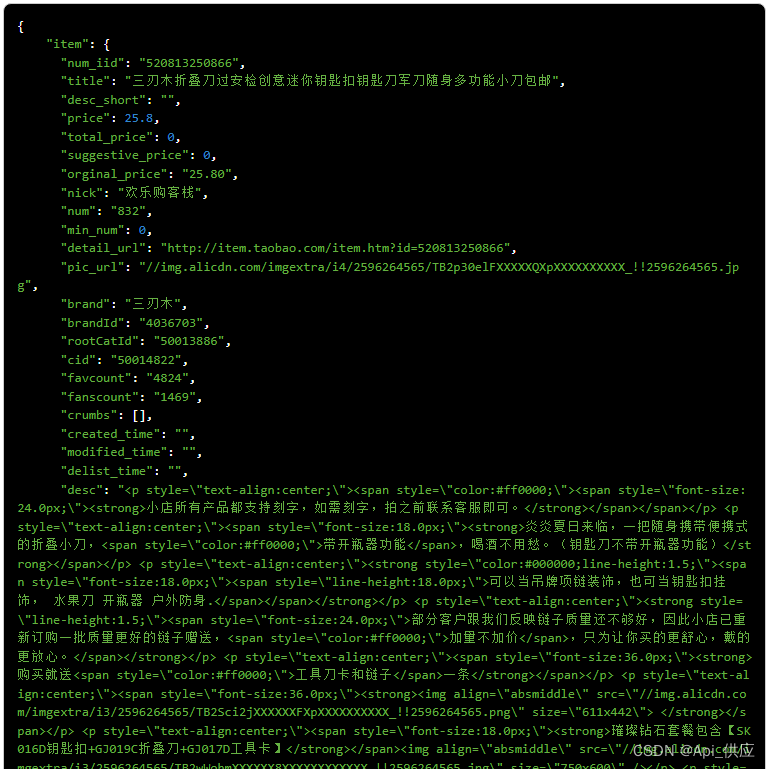
淘宝API(通过商品详情接口采集商品页面数据)请求说明文档|可接入测试key
淘宝商品详情数据接口(taobao.item_get)是天猫开放平台提供的一种API接口,旨在帮助开发者获取天猫平台上的商品详情信息。通过调用这个接口,开发者可以获取包括商品ID、标题、价格、库存量、图片等在内的详细数据,从而…...

示例说明闭包函数
示例说明闭包函数 闭包函数是指在一个函数内部定义另一个函数,并且内部函数可以访问外部函数的局部变量,即使外部函数已经执行完毕。 这种功能使得闭包函数可以捕获外部函数的状态,提供了一种保留局部变量值的方式。闭包函数在编程中常用于…...
【自媒体创作利器】AI白日梦+ChatGPT 三分钟生成爆款短视频
AI白日梦https://brmgo.com/signup?codey5no6idev 引言 随着人工智能(AI)技术的快速发展,AI在各个领域都展现出了强大的应用潜力。其中,自然语言处理技术的进步使得智能对话系统得以实现,而ChatGPT作为其中的代表之一…...

把握零碎时间,开启长期副业兼职之旅!在家也能轻松赚钱!
转眼间,2024年已悄然走过三分之一。这一年,外界环境似乎并不那么友好,但对我而言,我的月收入仍然相对稳定。我找到的副业让我每月能赚到3000元以上,这让我深感庆幸。 现实中,只依赖主业工资的日子确实艰辛…...

HarmonyOS开发实例:【数字管家app】
样例简介 数字管家场景需要手机端、设备端和服务端三方协同完成,本文档介绍的demo是数字管家大场景中的手机端应用;用户注册登录后可创建我的家庭并管理家庭成员;可以添加设备(包括智能台灯,智能窗帘,智能…...

人工智能_大模型033_LangChain003_记忆封装Memory上下文控制机制_LCEL表达式语言---人工智能工作笔记0168
## 三、记忆封装:Memory ### 3.1、对话上下文:ConversationBufferMemory from langchain.memory import ConversationBufferMemory, ConversationBufferWindowMemoryhistory = ConversationBufferMemory() history.save_context({"input": "你好啊"}…...

持安科技与顺丰正式签约!共建零信任应用安全最佳实践
近日,北京持安科技有限公司与顺丰科技有限公司基于零信任“应用数据网关产品”签署了合作协议,持安科技创始人兼CEO何艺、顺丰科技底盘领域负责人刘潭仁出席活动并签署协议。 根据协议,双方将基于持安科技的零信任应用数据网关产品展开合作与…...

Elasticsearch分布式搜索
实用篇-ES-环境搭建 ES是elasticsearch的简称。我在SpringBoot学习 数据层解决方案 的时候,写过一次ES笔记,可以结合一起看一下。 之前在SpringBoot里面写的相关ES笔记是基于Windows的,现在我们是基于docker容器来使用,需要你们提…...

【Unity 实用工具篇】 | UIEffect 实现一系列UGUI特效,灰度、负片、像素化特效
前言 【Unity 实用工具篇】 | UIEffect 实现一系列UGUI特效,灰度、负片、像素化特效一、UGUI特效插件:UIEffect1.1 介绍1.2 效果展示1.3 使用说明及下载 二、组件属性面板三、代码操作组件四、组件常用方法示例4.1 使用灰度特效做头像(关卡)选择 总结 前…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
