力扣15题. 三数之和
题目:
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
Python3代码解答:
class Solution:def threeSum(self, nums: List[int]) -> List[List[int]]:# 创建一个空列表result用来存放满足条件的三元组result = []# 给数组排序nums.sort()# 遍历数组for i in range(len(nums)):# 如果当前元素大于0,那么排序后的元素必定都大于0if nums[i] > 0:return result# 如果当前元素和上一个元素相同,则跳过当前循环# 如果 nums[i] 和 nums[i-1] 相同,那么基于 nums[i-1] 已经尝试过的所有# 可能的 left 和 right ,组合也会和基于 nums[i] 的组合重复if i > 0 and nums[i] == nums[i - 1]:continue# 设置两个指针,分别指向i之后的下一个元素和最后一个元素left = i + 1right = len(nums) - 1while right > left:# 计算三元组的和sum_ = nums[i] + nums[left] + nums[right]if sum_ < 0:# 如果 sum_ 小于 0,表示需要更大的数来抵消负数,因此将 left 指针向右移动一位left += 1elif sum_ > 0:# 如果 sum_ 大于 0,表示需要更小的数来减小总和,因此将 right 指针向左移动一位right -= 1else:# 如果 sum_ 等于 0,将当前三元组 [nums[i], nums[left], nums[right]] # 加入到结果列表 resultresult.append([nums[i], nums[left], nums[right]])# 在找到一个和为 0 的三元组后,为了避免添加重复的三元组# 需要在移动 left 和 right 指针之前跳过所有相同的元素# 如果 nums[right] 和它前一个元素 nums[right - 1] 相同,# 则 right 指针会继续向左移动while right > left and nums[right] == nums[right - 1]:right -= 1# 如果 nums[left] 和它后一个元素 nums[left + 1] 相同,# left 指针会继续向右移动,直到 nums[left] 的值改变# 这同样是为了防止因 left 指针位置的重复值导致的三元组重复while right > left and nums[left] == nums[left + 1]:left += 1# 完成这两个循环过后,指针 right 和 left 应该指向新的、非重复的元素# 然而,我们还需要进一步地将这两个指针分别向内移动一位right -= 1left += 1return result
上述代码解答:
上述代码实现的是 threeSum 方法,用于在给定整数数组 nums 中找出所有不重复的三元组(i.e., 三个数的组合),这些三元组的和为 0。方法的具体实现步骤如下:
-
初始化结果列表:创建一个空列表
result用来存放满足条件的三元组。 -
排序数组:首先对数组
nums进行排序。排序是为了之后更容易地使用双指针技术查找和为0的三元组。 -
遍历数组:通过一个 for 循环遍历排序后的数组,索引为
i。该索引代表三元组中的第一个数。 -
提前停止条件:如果当前元素
nums[i]大于 0,由于数组已经排序,后面的所有元素都会大于 0,因此不可能再找到和为 0 的三元组,直接返回已找到的结果result。 -
避免重复元素:为了避免找到重复的三元组,如果当前元素与前一个元素相同(
nums[i] == nums[i - 1]),则跳过当前循环的迭代。 -
双指针查找:设置两个指针
left和right,分别指向i之后的下一个元素和数组的最后一个元素。这两个指针会帮助找到与nums[i]相加和为 0 的两个数。 -
双指针移动:
- 计算当前三元组的和
sum_。如果sum_小于 0,表示需要更大的数来抵消负数,因此将left指针向右移动一位。 - 如果
sum_大于 0,表示需要更小的数来减小总和,因此将right指针向左移动一位。 - 如果
sum_等于 0,将当前三元组 [nums[i], nums[left], nums[right]] 加入到结果列表result。
- 计算当前三元组的和
-
避免添加重复的三元组:在找到一个和为 0 的三元组后,为了避免添加重复的三元组,需要在移动
left和right指针之前跳过所有相同的元素。 -
结果返回:循环结束后,返回结果列表
result,其中包含了所有不重复的和为 0 的三元组。
重难点解答:
解释如何在 threeSum 方法中避免添加重复的三元组:
1. 排序
首先,对数组进行排序是基础,它使得相同的数字都相邻,这有助于后续步骤中识别和跳过重复的元素。
2. 跳过处理中的重复元素
为了确保不添加重复的三元组,有两种主要的情况需要处理:
a. 跳过相同的起始元素
当遍历数组以选择三元组的第一个元素 nums[i] 时,如果当前的元素和前一个元素相同(即 nums[i] == nums[i-1]),并且 i 大于 0,则跳过当前的元素。这是因为如果 nums[i] 和 nums[i-1] 相同,那么基于 nums[i-1] 已经尝试过的所有可能的 left 和 right 组合也会和基于 nums[i] 的组合重复。因此,可以安全地跳过,不遗漏任何独特的三元组。
b. 找到和为零后跳过相同的 left 和 right
当找到一个和为零的三元组 [nums[i], nums[left], nums[right]] 后,我们添加这个三元组到结果列表中。然后,在移动 left 和 right 以寻找下一个可能的和为零的组合之前,我们跳过所有和当前 nums[left] 和 nums[right] 相同的元素。
- 对
left的处理:增加left指针,直到nums[left]的下一个元素不同于当前nums[left]。 - 对
right的处理:减少right指针,直到nums[right]的前一个元素不同于当前nums[right]。
这样做是因为,如果不跳过相同的 left 和 right,那么即使 i 是不同的,新的 [nums[i], nums[left], nums[right]] 也只会是重复之前已经找到的三元组。
例子
考虑数组 [-1, -1, 0, 1, 1],排序后的数组中 -1 和 1 都重复出现。当第一次使用第一个 -1 作为 nums[i],并找到一个三元组 [-1, 0, 1] 后,如果我们不跳过第二个 -1 或者不在找到一个有效三元组后跳过相同的 left 和 right,那么将会再次添加相同的三元组 [-1, 0, 1],从而导致结果中有重复。
完整示例解析:
假设我们有一个排序后的数组:[-4, -1, -1, 0, 1, 2, 2],我们要找出所有和为零的三元组。
初始步骤:
- 设定
i=0,元素是-4。 left指向i+1,即索引1的位置,元素是-1。right指向数组的最后一个元素,索引6,元素是2。
查找过程:
- 计算和
-4 + (-1) + 2 = -3,这个和小于零,所以我们需要一个更大的数来平衡,即将left向右移动到索引2。此时left位置的元素仍是-1。 - 重新计算和
-4 + (-1) + 2 = -3,和仍小于零,再次将left向右移动到索引3,此时left的元素是0。 - 再次计算和
-4 + 0 + 2 = -2,和仍小于零,移动left到索引4,元素是1。 - 再次计算和
-4 + 1 + 2 = -1,和仍小于零,继续移动left,此时left指向索引5,元素仍是2。 - 再次计算和
-4 + 2 + 2 = 0,找到一个有效的三元组[-4, 2, 2]。
避免重复的关键步骤:
找到三元组 [-4, 2, 2] 后,我们需要移动 left 和 right 来寻找下一个可能的三元组。重要的是,在移动这些指针前,我们需要确保跳过所有重复的值,避免重复添加相同的三元组:
- 从当前位置,
right指针向左移动,跳过与当前right值相同的所有元素。在这个例子中,right已经在数组的末端,所以不需要移动。 left指针向右移动,跳过与当前left值相同的所有元素。但由于我们已经检查到末端,这个例子中不需要进一步移动。
代码解释:
while right > left and nums[right] == nums[right - 1]:right -= 1
这一段循环确保如果 nums[right] 和它前一个元素 nums[right - 1] 相同,则 right 指针会继续向左移动,直到 nums[right] 的值改变。这样做是为了避免重复的三元组。例如,如果 nums[right] 重复出现,那么已经添加过的三元组再次添加就是重复的。
则移动左边的同理。
综上,本文的对于力扣15. 三数之和的Python3解答,仅仅是个人学习资料记录,也十分高兴我的见解可以帮助其他的正在做这个题目的同学,基础较差,仅仅是个人见解,大神勿喷,欢迎交流,谢谢!
相关文章:

力扣15题. 三数之和
题目: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复…...

项目经理好还是产品经理好?入行必读!
在现代项目管理领域,产品经理Product Manager和项目经理Project Manager,两者虽都是PM,但两者在实际操作中却有着显著的区别,在各自的领域中承担着不同的岗位职责和工作。 项目经理跟产品经理两个证都挺受市场欢迎的,…...
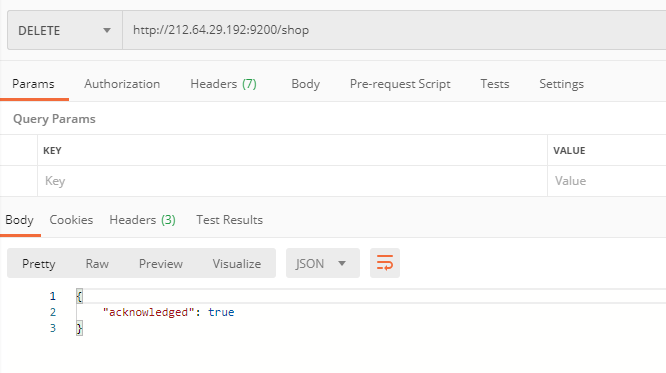
Elastic安装后 postman对elasticsearch进行测试
一、创建索引和mapping //id 字段自增id //good_sn 商品SKU //good_name 商品名称 //good_introduction 商品简介 //good_descript 商品详情 PUT http://IP:9200/shop { "mappings":{ "good":{ "properties":{ …...

JPA (Java Persistence API)
一、Jpa的介绍 JPA ,是一套Sun公司Java官方制定的ORM 规范。 ORM,即 对象关系映射 (Object Relational Mapping),是一种程序技术,用于 在关系数据库和业务实体对象之间做映射 。ORM 框架的存在,…...

实战要求下,如何做好资产安全信息管理
文章目录 一、资产安全信息管理的重要性二、资产安全信息管理的痛点三、如何做好资产安全信息管理1、提升资产安全信息自动化、集约化管理能力,做到资产全过程管理2、做好资产的安全风险识别3、做好互联网暴露面的测绘与管空4、做好资产安全信息的动态稽核管理 “摸…...
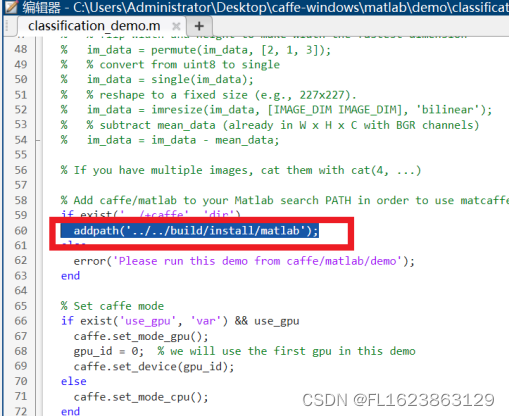
[matlab]matcaffe在matlab2023a安装和配置过程
测试环境: caffe-windows-cpu-py35-matlab2018b-vs2015-20220321 matlab2023a 注意:由于matlab新版本不允许添加特殊目录,比如有和private目录,添加后也会警告,但是可以忽略。因此可以使用我研发的matlab环境添加工具…...

【word2pdf】Springboot word转pdf(自学使用)
文章目录 概要整体介绍具体实现官网pom文件增加依赖 遇到的问题本地运行OK,发布到Linux报错还是本地OK,但是Linux能运行的,但是中文乱码 小结 概要 Springboot word 转 pdf 整体介绍 搜了一下,发现了能实现功能的方法有四种 U…...
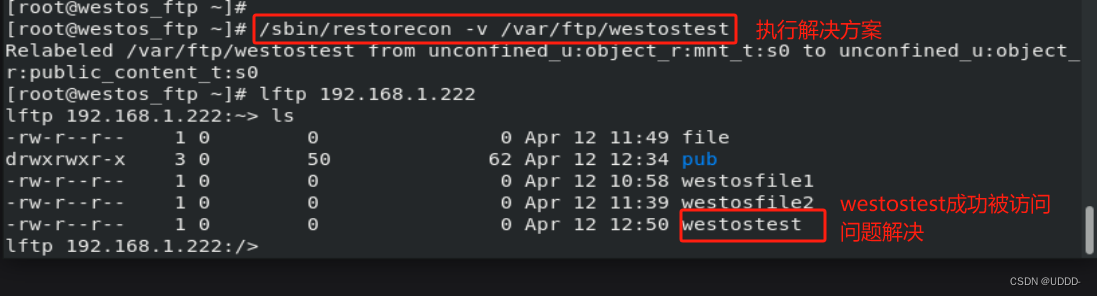
3_2Linux中内核级加强型火墙的管理
### 一.Selinux的功能 ### 观察现象 ①当Selinux未开启时 在/mnt中建立文件被移动到/var/ftp下可以被vsftpd服务访问 匿名用户可以通过设置后上传文件 当使用ls -Z /var/ftp查看文件时显示"?" ps auxZ | grep vsftpd 时显示: - root 8546 0.0 0.0 26952 …...

PCB工艺规范及PCB设计安规原则
一、目的 规范产品的PCB工艺设计,规定PCB工艺设计的相关参数,使得PCB的设计满足可生产性、可测试性、安规、EMC、EMI等的技术规范要求,在产品设计过程中构建产品的工艺、技术、质量、成本优势。 二、适用范围 本规范适用于所有电了产品的PCB工…...
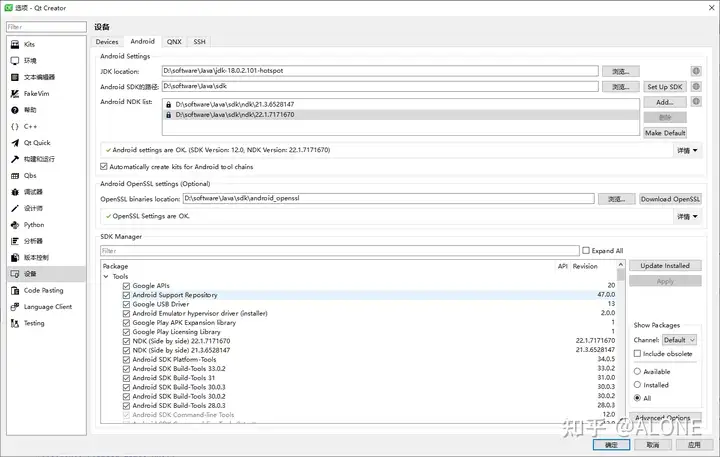
Qt for Android 开发环境
在搭建环境时开始感觉还挺顺利的,从 Qt 配置的环境里面看并没有什么问题,可真正编译程序的时候发现全是错误。 最开始的时候安装了 JDK21 最新版本,然后根据 JDK21 安装 ndk, build-tools, Platform-Tools 和 Gradle,但是不管这么…...
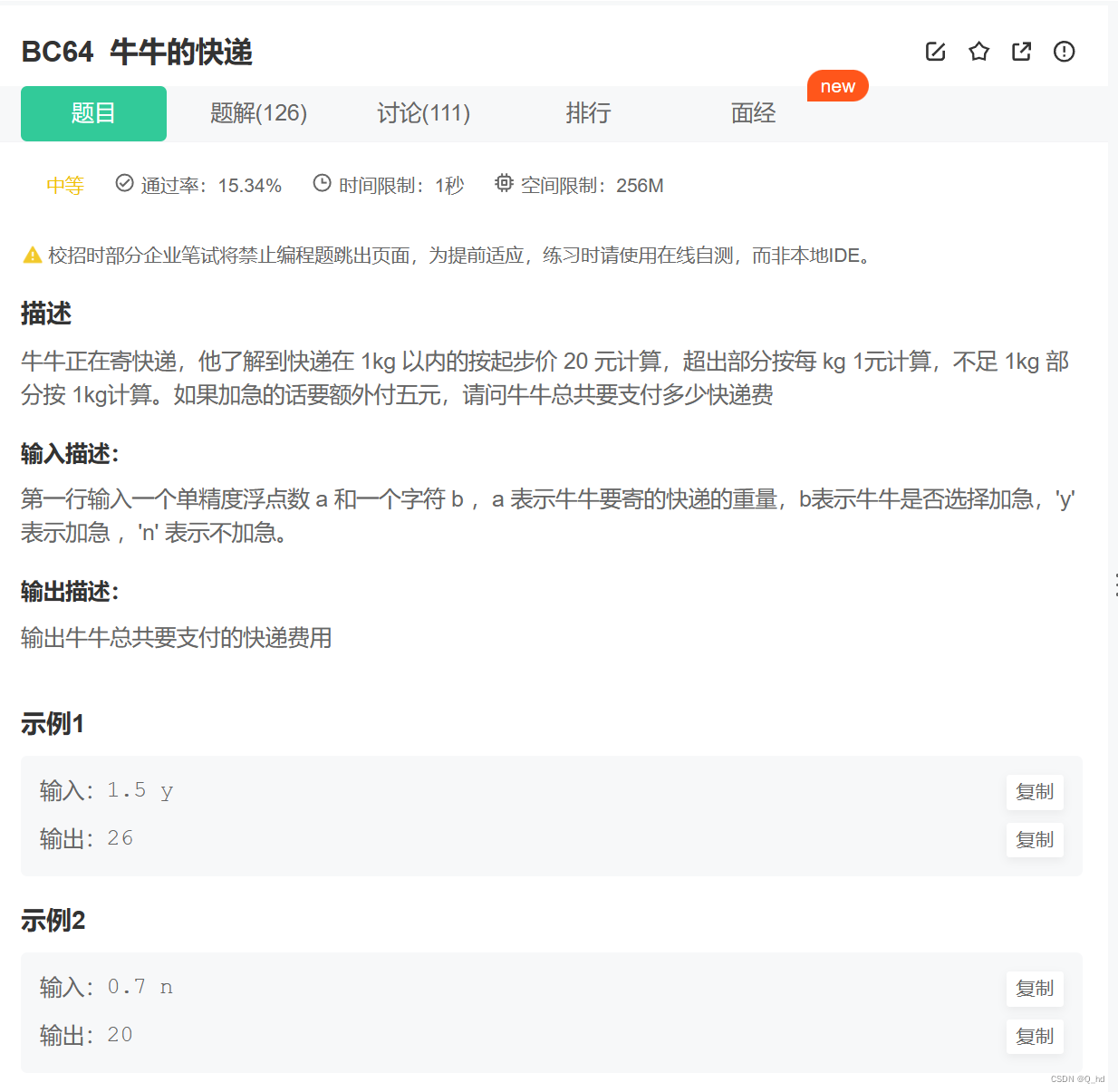
【题解】BC64 牛牛的快递(C++)
#include <iostream> #include<string> #include<math.h> using namespace std;int main() {int c0;string b;float a;cin>>a>>b;if(a>1)c20ceil(a-1);elsec20;if(b"y")c5;cout<<c; }在C中,ceil() 函数用于返回大…...

C++(运算符重载+赋值拷贝函数+日期类的书写)
目录 运算符重载运算赋值重载和运算赋重载前置和后置<,<,>,>,,!运算符重载日期类的实现<<流插入和>>流提取的运算符重载总结 运算符重载 C为了增强代码的可读性引入了运算符重载,运算符重载是具有特殊函数名的函数,也具有其 返回…...

【介绍下负载均衡原理及算法】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

CESS 受邀出席香港Web3.0标准化协会第一次理事会议,共商行业未来
2024 年 4 月 5 日,CESS(Cumulus Encrypted Storage System)作为香港 Web3.0 标准化协会的副理事会成员,于香港出席了 2024 年度第一次理事会会议。此次会议汇聚了来自不同领域的知名企业和专家(参会代表名单见文末&am…...
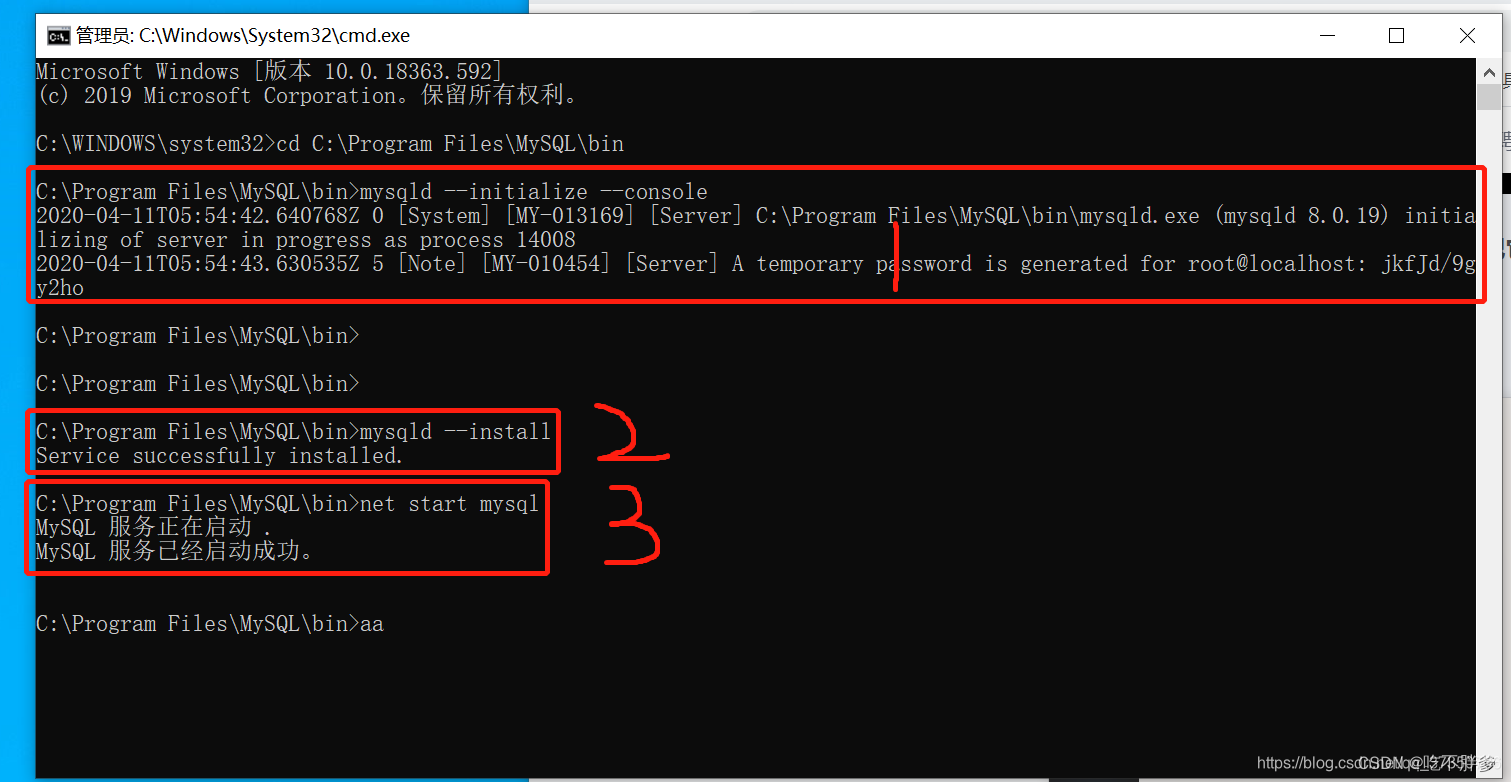
MySQL 8.0.19安装教程(windows 64位)
在c盘目录下的Program Files目录下创建MySQL目录,将下载好的mysql解压到里面 解压完是这个样子 配置初始化的my.ini文件的文件 [mysqld] # 设置3306端口 port3306 # 设置mysql的安装目录 basedirC:\Program Files\MySQL # 设置mysql数据库的数据的存放目录 datad…...
探索AI提示词网站:助力内容创作与AI对话
嗨,大家好!在这个充满创意的时代里,AI技术为我们带来了许多惊喜和便利。如果你是一个内容创作者,无论是在撰写博客还是进行科技对话,今天我将向大家介绍几个能够提升与AI对话效率的神奇网站。 1. FlowGPT 首先…...

AdaBoost 算法
目录 什么是 AdaBoost 算法? Adaboost 的 7 个优缺点 集成学习:人多力量大: Bagging:民主。Boosting :挑选精英。长短期记忆网络:引入遗忘机制 生成对抗网络 :物竞天择适者生存 首先,了解一下集成学习及 Boosting 算法 集成学习归属于机器学习,他是一种「训练思路…...

链接分析算法
链接分析(Link Analysis)通常指的是对图(Graph)中的节点(Nodes)和边(Edges)进行分析,以发现图的结构和属性。在图论中,链接分析算法通常用于解决诸如网页排名…...

怎么批量完成图片格式转换?介绍三种简单方法
在日常生活和工作中,我们经常会遇到需要将图片格式转换的情况,无论是为了适应不同的设备要求,还是为了能让我们的图片应用到更多的使用场景中去,批量图片格式转换都是一项非常实用的技能。本文将介绍一些常见的批量图片格式转换方…...
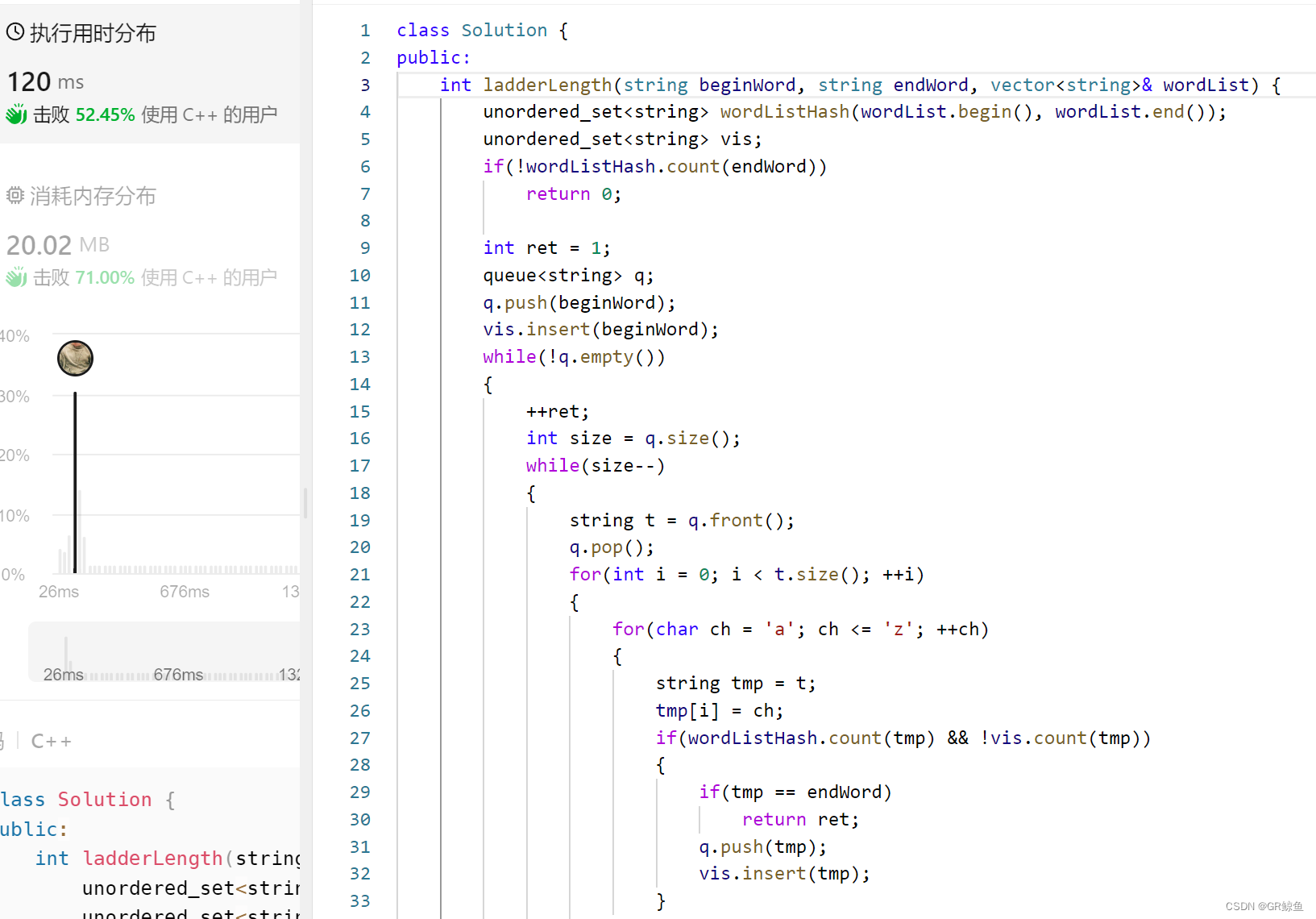
每日OJ题_BFS解决最短路③_力扣127. 单词接龙
目录 ③力扣127. 单词接龙 解析代码 ③力扣127. 单词接龙 127. 单词接龙 难度 困难 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk: 每一对相邻的单词只差一个字母。…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
