【数据结构】树与二叉树、树与森林部分习题以及算法设计例题 2
目录
- 【数据结构】树与二叉树、树与森林部分习题以及算法设计例题
- 一、交换二叉树每个结点的左右孩子
- Swap 函数(先序遍历):
- Swap 函数(中序遍历)××× 不可行:
- Swap 函数(后序遍历):
- 二、非递归算法求森林中有几棵树
- 树的二叉链表(孩子-兄弟)存储表示法
- 三、判断二叉树是否为完全二叉树
- 四、求二叉树的最小深度 以及 二叉树树高
- 树与二叉树知识点文章: 【数据结构】树与二叉树(递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法)
- 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用(求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子)
- 树与森林知识点文章: 【数据结构】树与森林(树的存储结构、森林与二叉树的转化、树与森林的遍历)
- 树与二叉树、树与森林部分习题: 【数据结构】树与二叉树、树与森林部分习题与算法设计例题
【数据结构】树与二叉树、树与森林部分习题以及算法设计例题
一、交换二叉树每个结点的左右孩子
以上代码实现了交换二叉树每个节点的左右孩子的功能,分别使用了先序、中序和后序遍历的方式。
遍历二叉树算法的变式:
-
Swap 函数(先序遍历):
- 从根节点开始,先交换当前节点的左右孩子。
- 然后递归地对左子树和右子树执行相同的操作。
-
Swap2 函数(中序遍历):
- 与先序遍历不同,中序遍历中需要先对左子树进行操作,然后交换当前节点的左右孩子,最后对右子树进行操作。
- 但是这个实现方式是错误的,因为在交换左子树之后,对右子树进行操作时,右子树的结构已经发生了变化,导致结果错误。
-
Swap3 函数(后序遍历):
- 与先序遍历类似,但是是在遍历完左右子树之后再交换当前节点的左右孩子。
- 这样可以保证在交换左右孩子时,左右子树的结构不会被改变。
通过上述分析,正确的交换方式是采用先序或后序遍历,中序遍历方式不适合这个场景。
Swap 函数(先序遍历):
//前序
void Swap(BiTree& T){//(先序遍历) if(T){//根节点 if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap(T->lchild);Swap(T->rchild);}
}
Swap 函数(中序遍历)××× 不可行:
//中序的不行
void Swap2(BiTree& T){//(中序遍历) if(T){//根节点 Swap2(T->lchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap2(T->rchild);}
}
Swap 函数(后序遍历):
//后序
void Swap3(BiTree& T){//(后序遍历) if(T){//根节点 Swap3(T->lchild);Swap3(T->rchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}}}
综上可行的只有先序和后序这两种方法:
//交换二叉树每个结点的左右孩子
//先序
void XXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//先序if(!T->lchild&&!T->rchild) return;p=T->lchild;T->lchild=T->rchild;T->rchild=p;XXSwap_LandRchild(T->lchild);XXSwap_LandRchild(T->rchild);}
}
//后序
void HXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//后序if(!T->lchild&&!T->rchild) return;HXSwap_LandRchild(T->lchild);HXSwap_LandRchild(T->rchild);p=T->lchild;T->lchild=T->rchild;T->rchild=p;}
}
完整代码示例:
//设二叉树采用二叉链表存储,设计递归算法实现二叉树中所有结点的左右孩子交换。
#include<iostream>
using namespace std;//二叉链表
typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (BiTNode*)malloc(sizeof(BiTNode));T->data = ch; // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}void XXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//先序if(!T->lchild&&!T->rchild) return;p=T->lchild;T->lchild=T->rchild;T->rchild=p;XXSwap_LandRchild(T->lchild);XXSwap_LandRchild(T->rchild);}
}void HXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//后序if(!T->lchild&&!T->rchild) return;HXSwap_LandRchild(T->lchild);HXSwap_LandRchild(T->rchild);p=T->lchild;T->lchild=T->rchild;T->rchild=p;}
}void XXPrintTree(BiTree T){if(T==NULL) return;else{cout<<T->data<<" ";XXPrintTree(T->lchild);XXPrintTree(T->rchild);}
}int main()
{BiTree T;CreateBiTree(T);XXPrintTree(T);cout<<endl;XXSwap_LandRchild(T);XXPrintTree(T);cout<<endl;HXSwap_LandRchild(T);XXPrintTree(T);cout<<endl;return 0;
}
二、非递归算法求森林中有几棵树
树的二叉链表(孩子-兄弟)存储表示法
[fc,data,nb]
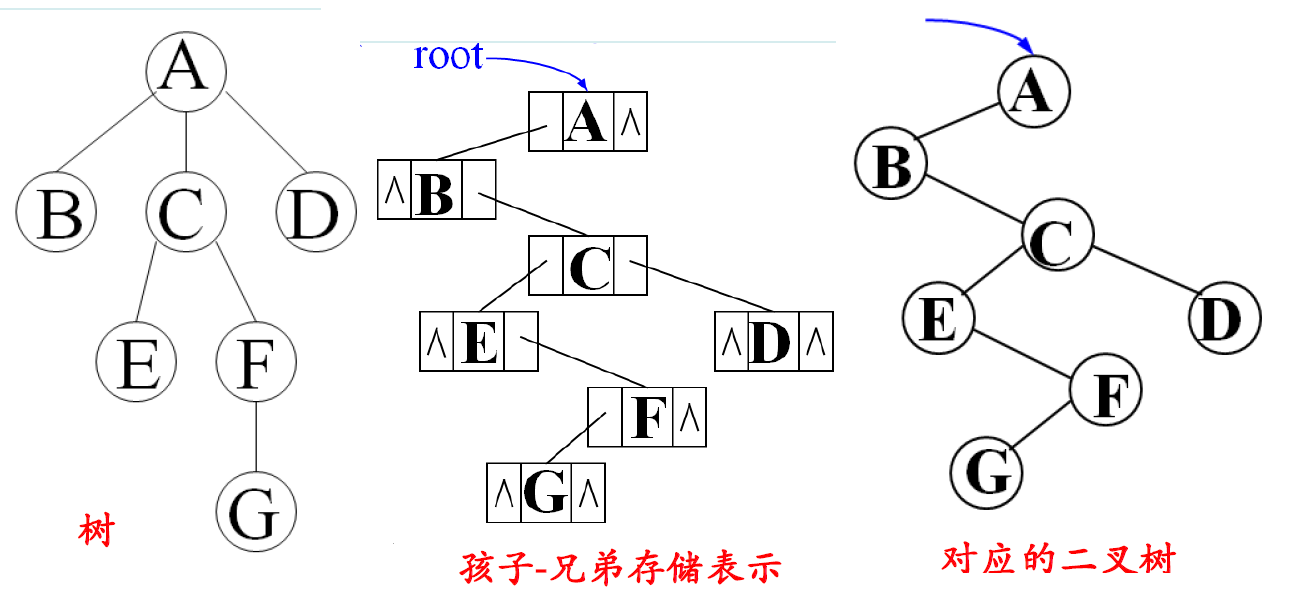
typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;
树中每个结点三部分:
数据域(data),长子指针域(fc),
右邻兄弟指针域(nb)
树和二叉树的转换
• 树以孩子兄弟表示法存,相当于将树转换成二叉树,但此二叉树根结点无右子树
• 好处:借助二叉树的操作实现树的操作
森林与二叉树的转换
⮚ 树采用二叉链表(孩子-兄弟)存储表示法,转换成二叉树
⮚ 森林由多棵树组成: F = ( T 1 , T 2 , … , T n ) F = ( T1, T2, …, Tn ) F=(T1,T2,…,Tn); 将其每棵树转换成二叉树 B T 1 , B T 2 , … , B T n BT₁, BT₂, …, BTn BT1,BT2,…,BTn;
⮚ 每棵二叉树BT的根的右子树皆为空树,从BTn开始依次将其根结点链为前一棵二叉树的根的右孩子
⮚ 将森林转换成一棵二叉树,森林的操作可借助二叉树的操作完成
森林和二叉树的转换
• 森林以孩子兄弟表示法存,相当于将森林转换成二叉树
• 好处:借助二叉树的操作实现森林的操作
因此只需要一直向右下数结点的个数就行:
typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;//非递归算法求森林中有几棵树。
int CountForestTrees(CSTree F){CSTree p=F;int num=1;while(p){p=p->nb;//右子树num++;}return num;
}完整代码示例:
//设森林采用根节点为T的二叉链表存储,设计非递归算法求森林中有几棵树。
#include<iostream>
using namespace std;typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(CSTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (CSNode*)malloc(sizeof(CSNode));T->data = ch; // 生成根结点CreateBiTree(T->fc); // 构造左子树CreateBiTree(T->nb); // 构造右子树}
}//非递归算法求森林中有几棵树。
int CountForestTrees(CSTree F){CSTree p=F;int num=1;while(p){p=p->nb;//右子树num++;}return num;
}int main()
{CSTree T;CreateBiTree(T);cout<<"森林一共有"<<CountForestTrees(T)<<"棵树"<<endl;return 0;
}
三、判断二叉树是否为完全二叉树
判断二叉树是否为完全二叉树的函数:
//完全二叉树的性质
bool check(BiTree T){if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))return true;return false;
} //判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){BiTree p=T;SqQueue Q;if(!T) return true;//空树也是完全二叉树InitQueue(Q);EnQueue(Q,p);while(!is_QueueEmpty(Q)){DeQueue(Q,p);if(!check(p)) return false;else{if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}}return true;
}
(带main函数)题解代码示例:
//给定一个二叉树,找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。#include<iostream>
using namespace std;//判断二叉树是否为完全二叉树//结点定义入下:
//二叉链表
typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;//若用到队列,请用循环队列,并请实现队列的相关操作以供调用。#define MAXQSIZE 100typedef struct {BiTree *base;int front,rear;
} SqQueue; //定义循环队列//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (BiTNode*)malloc(sizeof(BiTNode));T->data = ch; // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}
//队列的初始化
void InitQueue(SqQueue &Q){Q.base = (BiTree *)malloc(MAXQSIZE*sizeof(BiTree));Q.front = Q.rear = 0;//队列初始化
}//队空
bool is_QueueEmpty(SqQueue Q){if(Q.rear==Q.front) return true;return false;
}//队满
bool is_QueueMAX(SqQueue Q){if((Q.rear+1)%MAXQSIZE == Q.front) return true;return false;
}//入队
void EnQueue(SqQueue &Q,BiTree e){if(!is_QueueMAX(Q)){Q.base[Q.rear]=e;Q.rear = (Q.rear + 1) % MAXQSIZE;}else{cout<<"ERROR!!! 队列已满"<<endl;}
}
//出队
void DeQueue(SqQueue &Q,BiTree &e){if(!is_QueueEmpty(Q)){e = Q.base[Q.front];Q.front = (Q.front + 1) % MAXQSIZE;}else{cout<<"ERROR!!! 队列为空"<<endl;}
}//完全二叉树的性质
bool check(BiTree T){if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))return true;return false;
} //判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){BiTree p=T;SqQueue Q;if(!T) return true;//空树也是完全二叉树InitQueue(Q);EnQueue(Q,p);while(!is_QueueEmpty(Q)){DeQueue(Q,p);if(!check(p)) return false;else{if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}}return true;
}//层次遍历算法
void LevelOrderTraverse(BiTree T)
{ BiTree p = T;SqQueue Q;if(!T) return; InitQueue(Q); EnQueue(Q,p);while (!is_QueueEmpty(Q)){ DeQueue(Q,p);printf("%c ", p->data);if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}
}int main(){BiTree T;//例如输入:ABC##DE##F### 来创建二叉树 CreateBiTree(T);LevelOrderTraverse(T);cout<<endl;if(is_Complete_Binarytree(T)){cout<<"是完全二叉树"<<endl;}else{cout<<"不是完全二叉树"<<endl;}return 0;
} 四、求二叉树的最小深度 以及 二叉树树高
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
求二叉树的最小深度的函数:
//直接就是将求树高的程序进行修改,将找左右子树最大树高 改为求左右子树 最小树高
//求二叉树的最小深度
int Get_minHeigt(BiTree T){//二叉树的最小深度if(T==NULL) return 0;else{int Left_Height = Get_minHeigt(T->lchild);int Right_Height = Get_minHeigt(T->rchild);int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径return Tree_minHeight;}}
(带main函数)题解代码示例:
//给定一个二叉树,找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。#include<iostream>
using namespace std;typedef struct TreeNode{int data;//数据域TreeNode *rchild;//右孩子指针TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (TreeNode*)malloc(sizeof(TreeNode));T->data = ch; // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}//求树高
int Get_Height(BiTree node){//递归 求树高 if(node==NULL) return 0;else{int Left_Height = Get_Height(node->lchild);int Right_Height = Get_Height(node->rchild);int Tree_Height = 1 + (Left_Height > Right_Height?Left_Height:Right_Height);//计算树高return Tree_Height;}}
//求二叉树的最小深度
int Get_minHeigt(BiTree T){//二叉树的最小深度if(T==NULL) return 0;else{int Left_Height = Get_minHeigt(T->lchild);int Right_Height = Get_minHeigt(T->rchild);int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径return Tree_minHeight;}}int main(){BiTree T;//例如输入:ABC##DE##F### 来创建二叉树 CreateBiTree(T);cout<<"树高为:" ;cout<<Get_Height(T)<<endl;cout<<"根节点到叶节点的最短路径上的节点数量为:";cout<<Get_minHeigt(T)<<endl;return 0;
} 感谢阅读!!!
- 树与二叉树知识点文章: 【数据结构】树与二叉树(递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法)
- 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用(求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子)
- 树与森林知识点文章: 【数据结构】树与森林(树的存储结构、森林与二叉树的转化、树与森林的遍历)
- 树与二叉树、树与森林部分习题: 【数据结构】树与二叉树、树与森林部分习题与算法设计例题
相关文章:

【数据结构】树与二叉树、树与森林部分习题以及算法设计例题 2
目录 【数据结构】树与二叉树、树与森林部分习题以及算法设计例题一、交换二叉树每个结点的左右孩子Swap 函数(先序遍历):Swap 函数(中序遍历) 不可行:Swap 函数(后序遍历)ÿ…...

Cesium之home键开关及相机位置设置
显隐控制 设置代码中的homeButton var TDT_IMG_C "https://{s}.tianditu.gov.cn/img_c/wmts?servicewmts&requestGetTile&version1.0.0" "&LAYERimg&tileMatrixSetc&TileMatrix{TileMatrix}&TileRow{TileRow}&TileCol{TileCol}…...
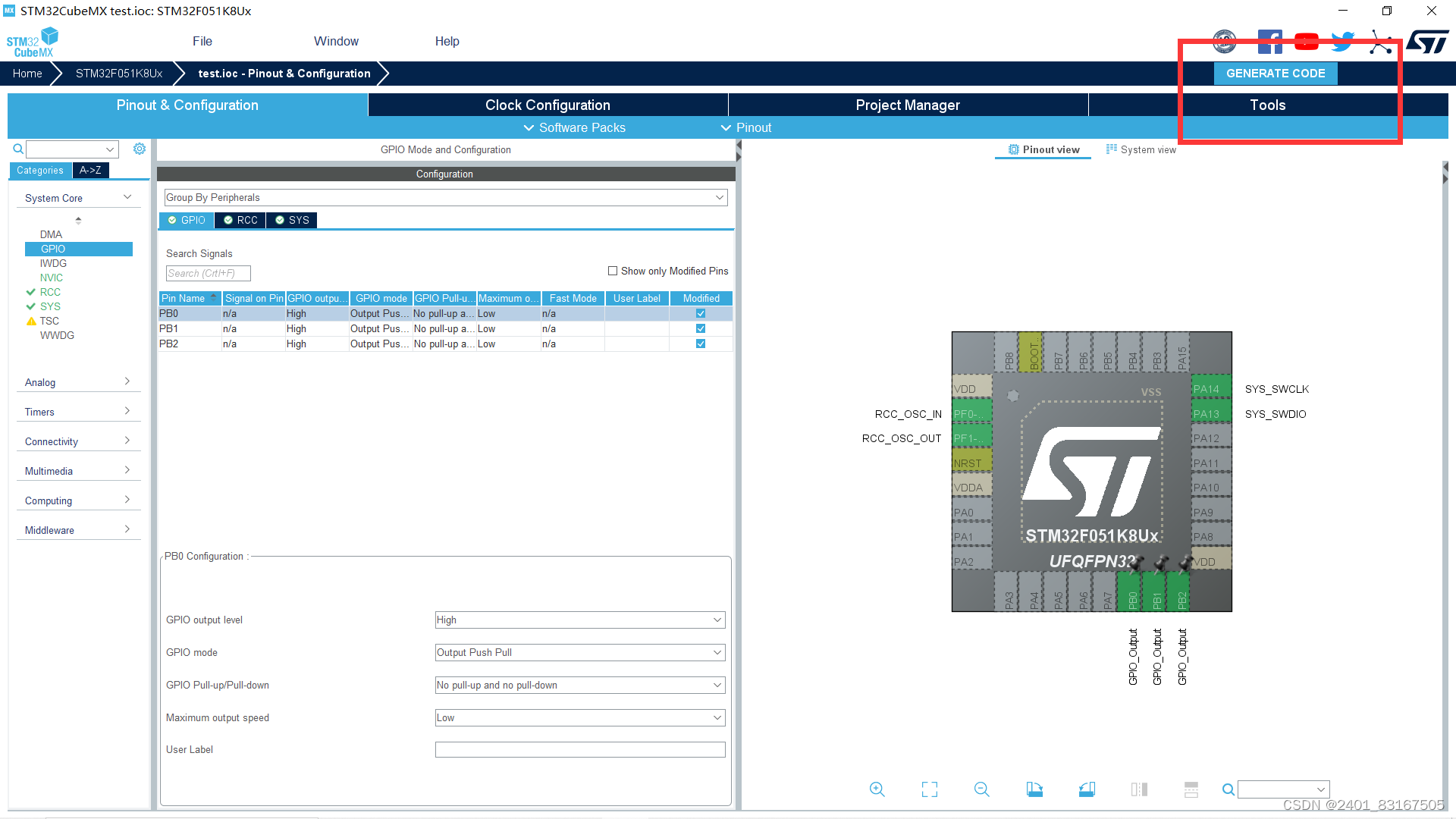
FreeRTOS_day1
1.总结keil5下载代码和编译代码需要注意的事项 下载代码前要对仿真进行设置 勾选后代码会立刻执行 勾选后会导致代码不能执行 写代码的时候要写在对应的begin和end之间,否则会被覆盖 2.总结STM32Cubemx的使用方法和需要注意的事项 ①打开软件,新建工程…...

Nginx日志格式化和追踪
背景 Nginx是一款功能强大的Web服务器,对于网络环境中的日志记录和配置至关重要。定制化Nginx日志格式可以帮助管理员更好地监控服务器性能、分析用户行为并做出相应优化。在本文中,我们将深入探讨Nginx日志格式的高级定制化策略,包括理解基…...

华为交换机配置telnet SSH登录步骤
这次项目中的交换机是华为 S5735-L24T4X 需要配置telnet和 SSH登录 在平时项目中发现,华为不同型号,不同版本的配置命令也是不同,(这不是脑子有问题吗? 干啥搞成不一样的) 本次型号:S5735-L2…...

市面上加密混淆软件的比较和推荐
引言 市面上有许多加密混淆软件可供开发者使用,但哪些软件是最好用的?哪些软件受到开发者的喜爱?本文将根据一次在CSDN上的投票结果,为大家介绍几款在程序员中普及度较高的加密软件。以下是投票结果,希望能对大家的选择…...

最新AI创作系统ChatGPT网站源码AI绘画,GPTs,AI换脸支持,GPT联网提问、DALL-E3文生图
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧。已支持GPT…...

电视盒子哪个好?2024口碑网络电视盒子排行榜
多年来电视盒子始终占据重要地位,功能上并没有受到影响。在这么多品牌中哪些电视盒子的评价是最好的呢?小编根据各大电商平台的用户评价情况整理了口碑最好的网络电视盒子排行榜,跟着小编一起看看市面上的电视盒子哪个好吧。 TOP 1࿱…...

CookieSession
目录 什么是会话 一.Cookie 1.Cookie介绍 2.Cookie的作用 3.Cookie的基本使用 4.Cookie生命周期 5.Cookie有效路径 6.注意事项 二.Session 1.Session基本原理 2 Session的作用 3.Session的基本使用 4.Session底层实现机制 5.Session生命周期 什么是会话 Cookie和S…...
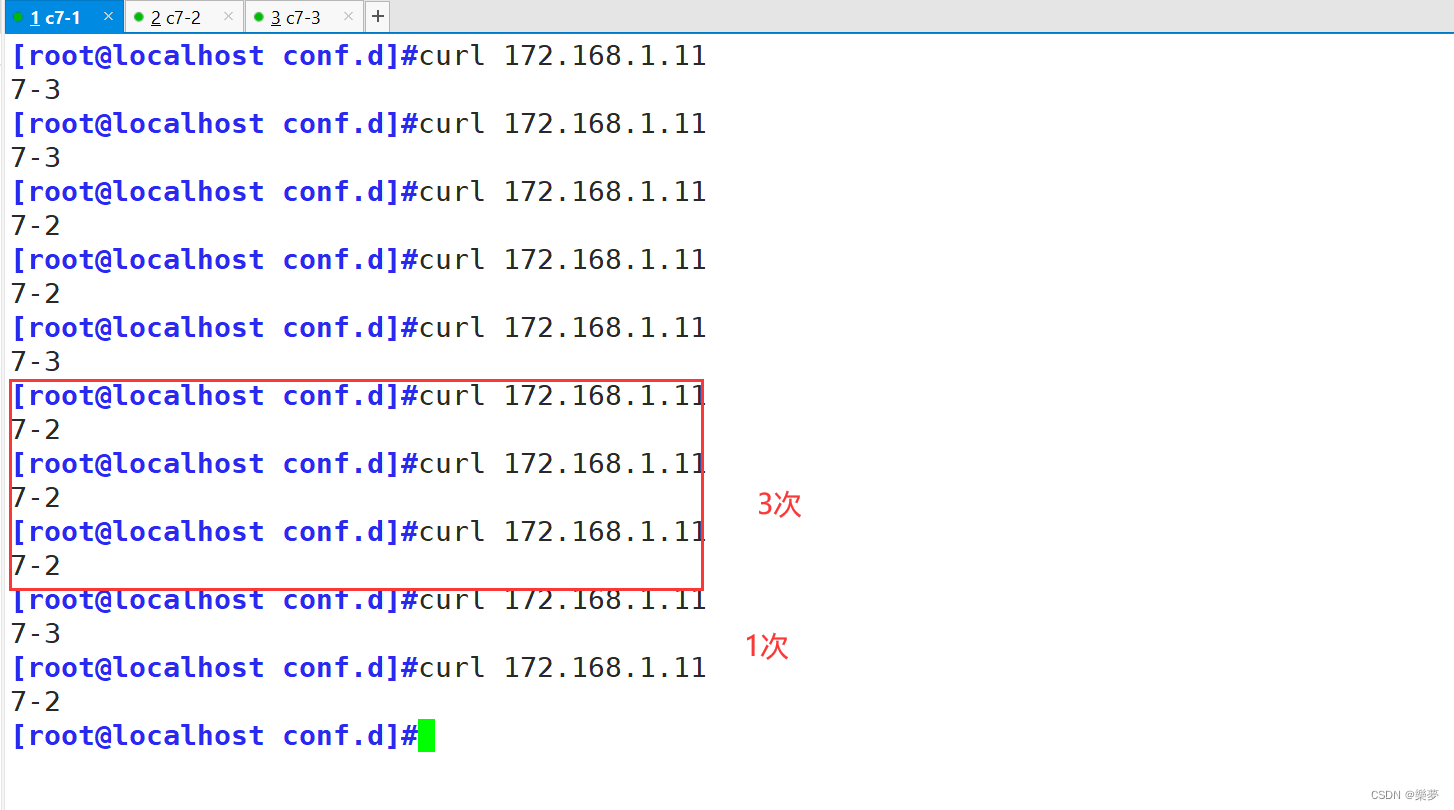
Nginx服务 重写功能与反向代理
六、重写功能 rewrite Nginx服务器利用 ngx_http_rewrite_module 模块解析和处理rewrite请求,此功能依靠 PCRE(perl compatible regular expression),因此编译之前要安装PCRE库,rewrite是nginx服务器的重要功能之一,用于实现URL的…...

Midjourney教程(完整版)-看这篇就够了
Midjourney使用指南 - 订阅计划费用比较 Midjourney 具有三个订阅版本。按月或全年支付可享受 20% 的折扣。每个订阅计划都包括访问 Midjourney 图库、官方 Discord、一般商业使用条款等。 如何订阅 使用该/subscribe命令生成指向订阅页面的个人链接。 或者,转到Mi…...

服务器上部署GPU版的milvus向量数据库
1、安装docker compose 我们可以从 Github 上下载它的二进制包来使用,最新发行的版本地址: https://github.com/docker/compose/releases sudo curl -L "https://github.com/docker/compose/releases/download/v2.6.0/docker-compose-$(uname -s)…...

【配置】Docker安装可道云网盘
环境 一台云服务器,centos8,必须安装docker Docker安装 1、卸载旧版 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine2、需要的安装包 yum ins…...

复盘中得道,技术人的自由之路
从今天开始,后面会推出一个系列,也就是「复盘中得道,技术人的自由之路」。 如果再给我一次机会,我会这样规划我的成长路线,实现职业自由、财富自由、身心自由。 如果你站在童年的位置瞻望未来,你会说你前…...

Nginx配置大全【六大使用场景、七大负载均衡策略、四大负载健康检查】
目录 基础配置信息应用场景一:配置web服务器应用场景二:反向代理服务器应用场景三:URL重定向应用场景四:防盗链应用场景五:根据设备类型重定向/代理/访问 不同域名/资源应用场景六:!负载均衡服务…...

GDPU Java 天码行空8
文章目录 (一)实验目的(二)实验内容和步骤1、LinkedList 实现队列💖 MyQueueDemo.java💖 运行结果: 2、集合的嵌套遍历💖 StudentDemo.java💖 运行结果: 3、类…...

《前端面试题》- JS基础 - 伪数组
第一次听说伪数组这个概念,听到的时候还以为是说CSS的伪类呢,网上一查,这东西原来还是个很常见的家伙。 何为伪数组 伪数组有两个特点: 具有length属性,其他属性(索引)为非负整数但是却不具备…...

TypeScript 基础语法
文章目录 1. 类型注解2. 接口(Interfaces)3. 类(Classes)4. 泛型(Generics)5. 枚举(Enums)6. 高级类型7. 模块8. 装饰器(Decorators)9. 映射类型(…...

服务器数据恢复—V7000存储raid5数据恢复案例
服务器数据恢复环境: P740AIXSybaseV7000存储阵列柜,阵列柜上有12块SAS机械硬盘(包括1块热备盘)。 服务器故障: 管理员在日常巡检过程中发现阵列柜中有一块磁盘发生故障,于是更换磁盘并同步数据࿰…...

扫雷 【搜索,哈希】
9.扫雷 - 蓝桥云课 (lanqiao.cn) #include<bits/stdc.h> using namespace std; #define int long long const int N1e5100; int n,m,res0; struct pt{int x,y,r; }; typedef pair<int,int> pii; map <pii,int> a;//炸雷的map,键是x,y,值是r map <pii,int&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...

CCF 开源发展委员会 “开源高校行“ 暨红山开源 + OpenAtom openKylin 高校行活动在西安四所高校成功举办
点击蓝字 关注我们 CCF Opensource Development Committee CCF开源高校行 暨红山开源 openKylin 高校行 西安站 5 月 26 日至 28 日,CCF 开源发展委员会 "开源高校行" 暨红山开源 OpenAtom openKylin 高校行活动在西安四所高校(西安交通大学…...

《开篇:课程目录》
大家好!我是一名.NET技术开发者,长期以来积累了比较多的项目实战经验,现在把它分享给大家,希望能够帮助到大家,同时为.NET社区提供一份力量,让更多的开发者参与进来。 要讲解的课程如下: 《介绍…...

使用MounRiver Studio Ⅱ软件写一个CH592F芯片的ADC采集程序,碰到的问题
MounRiver Studio Ⅱ 默认是不开启浮点计算的,所以有些浮点功能不能用,碰到问题是 while (1) {DelayMs (100);tmp Read_Temperature (0);sprintf (tempBuffer, "temp:%.2f\r\n", tmp); // 格式化温度值到字符串。使用%f要开启相应的…...
