MindOpt APL向量化建模语法的介绍与应用(2)
前言
在数据科学、工程优化和其他科学计算领域中,向量和矩阵的运算是核心组成部分。MAPL作为一种数学规划语言,为这些领域的专业人员提供了强大的工具,通过向量式和矩阵式变量声明以及丰富的内置数学运算支持,大大简化了数学建模和优化问题的处理。在本文中,我们将探索MAPL的这些特性,并且通过示例来展示如何有效使用这些工具。
介绍与应用
矩阵和向量变量声明
在MAPL中,向量和矩阵变量的声明非常直观。例如,使用var X(3,2)可以创建一个3行2列的矩阵,而使用var Y(3)会创建一个包含3个元素的列向量。对这些变量的操作,如索引(X[1,0])和赋予初值,都可以使用易于理解的语法来完成。
var X(3,2) >=0 integer;print "Structure of X is:";
print X;print "----------------";
print "Sample Entries:";
print X[0,0];
print X[1,1];
print X[2,1];
结果如下:
Structure of X is:
[[ X0, X1],[ X2, X3],[ X4, X5]]
----------------
Sample Entries:
+ [0, 0] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000
+ [1, 1] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000]
+ [2, 1] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000]
张量运算支持
张量运算是MAPL中一项强大的特性,它允许我们使用类似于线性代数中的标准操作符,例如:
- 加法和减法(+,-):逐元素进行操作,要求操作数尺寸相同。
- 乘法(*):支持标量和矩阵的乘法,以及矩阵与向量之间的乘法,必须满足传统的行列匹配规则。
- 转置('):快速提供变量的转置形式,仅适用于矩阵。
- 点乘(.*):逐元素乘法,用于两个相同尺寸的矩阵或向量。| 类型 | 操作符 | 说明 | 是否支持标量 | 用例 |
| ---------- | ------ | ------------------------- | ------------ | ----------------- |
| 一元操作符 |+| 向量/矩阵加法 | 是 |X+Y|
| |-| 向量/矩阵减法,或者求反 | 是 |X-Yor-X|
| |.*| 逐元素乘法 | 否 |X.*Y|
| |*| 向量/矩阵乘法 | 是 |X*Y|
| |'| 矩阵转置 | 否 |X'|
| |/| 向量/矩阵逐元素除以某标量 | 是 |X/2|
| 二元操作符 |^| 逐元素的p次幂 | 是 |X^2|
| 索引操作符 |[]| 获取指定位置的值 | 否 |X[3], Y[3,5]|
这些运算符为建模提供了极大的灵活性和表现力,支持以直观和自然的方式表达数学关系。
映射函数
映射函数是处理张量式变量必不可少的一部分,使建模张量间的函数变换更方便。MAPL提供了一系列映射函数,如exp、log和sin等,它们可以逐元素应用于向量或矩阵。例如,对于一个矩阵A,exp(A)会计算A中每个元素的指数值。
clear model;
var x(3,2) >=0;A = exp(x);print A;
运行上述代码,结果如下:
[[e^(x0), e^(x1)],[e^(x2), e^(x3)],[e^(x4), e^(x5)]]
混合计算和表达式引用
MAPL不仅支持张量间的运算,还支持张量和标量之间的混合计算。此外,它允许用户为复杂的表达式命名,以便于后续引用,这样可以避免重复的计算,并使模型清晰易于管理。
var x >=0;
var y(3,4);A = x + y;
B = y + x;
C = x - y;
D = y - x;
E = -y;
F = x*y;print y;
print A;
print B;
print C;
print D;
print E;
print F;
输出如下:
[[ y0, y1, y2, y3],[ y4, y5, y6, y7],[ y8, y9, y10, y11]][[ x+y0, x+y1, x+y2, x+y3],[ x+y4, x+y5, x+y6, x+y7],[ x+y8, x+y9, x+y10, x+y11]][[ y0+x, y1+x, y2+x, y3+x],[ y4+x, y5+x, y6+x, y7+x],[ y8+x, y9+x, y10+x, y11+x]][[ x-y0, x-y1, x-y2, x-y3],[ x-y4, x-y5, x-y6, x-y7],[ x-y8, x-y9, x-y10, x-y11]][[ y0-x, y1-x, y2-x, y3-x],[ y4-x, y5-x, y6-x, y7-x],[ y8-x, y9-x, y10-x, y11-x]][[ -y0, -y1, -y2, -y3],[ -y4, -y5, -y6, -y7],[ -y8, -y9, -y10, -y11]][[ x*y0, x*y1, x*y2, x*y3],[ x*y4, x*y5, x*y6, x*y7],[ x*y8, x*y9, x*y10, x*y11]]一个完整示例
带资源上限约束的二分匹配问题(也称为加权二分匹配问题或指派问题)是图论中的一个经典问题,它的目的是在二分图中找到最优的匹配,使得匹配的总权重最大,同时不超过给定的资源上限。
线性数学建模如下:
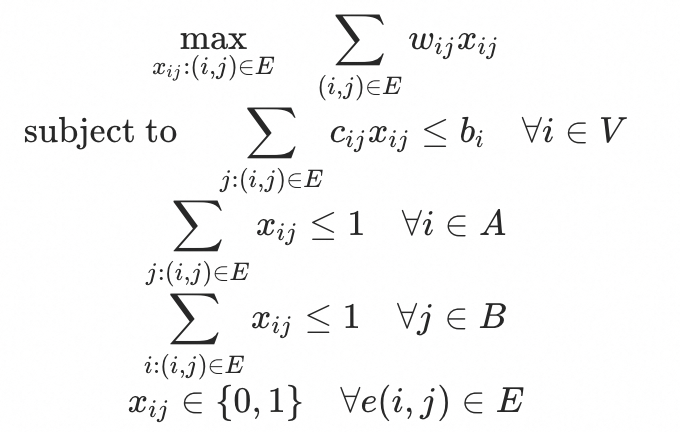
向量形式:
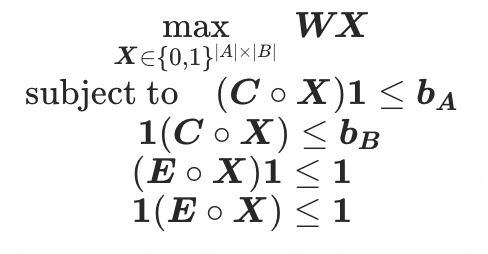
代码建模如下,可复制在云上平台直接运行:
########################################
#
# 向量式建模案例
# Weighted Bipartite Matching
#
######################################### 1.读取权重及损耗矩阵
param W = read_csv("weight.data");
param C = read_csv("cost.data");param m = W.row;
param n = W.col;############## 2.问题建模 ###############
# 定义矩阵形式变量X,表示可行的匹配
var X(m, n) binary; # 3.二分匹配问题建模
maximize sum(W.*X);# A集合的资源上限约束
s.t. (C.*X)*ones(n,1) <= 10;
# B集合的资源上限约束
s.t. ones(1,m)*(C.*X) <= 10;# 集合A中每个节点最多匹配一次
s.t. X * ones(n, 1) <= 1;
# 集合B中每个节点最多匹配一次
s.t. ones(1, m) * X <= 1;############## 问题求解 #################
# 3.调用mindopt求解
option solver mindopt;
solve;############## 结果分析 #################
# 输出最优目标函数值
param obj = sum(W.*X);
print "Optimal obj is: {:.2f}" % obj;# 输出最优匹配
print "Optimal X is";
print X;
#######################################
输出结果如下:
Running mindoptampl
wantsol=1
MindOpt Version 1.0.1 (Build date: 20231114)
Copyright (c) 2020-2023 Alibaba Cloud.Start license validation (current time : 05-FEB-2024 10:34:07).
License validation terminated. Time : 0.008sModel summary.- Num. variables : 50- Num. constraints : 30- Num. nonzeros : 200- Num. integer vars. : 50- Bound range : [1.0e+00,1.0e+01]- Objective range : [4.0e-01,9.8e+00]Branch-and-cut method started.
Original model: nrow = 30 ncol = 50 nnz = 200
Tolerance: primal = 1e-06 int = 1e-06 mipgap = 0.0001 mipgapAbs = 1e-06
Limit: time = 1.79769313486232e+308 node = -1 stalling = -1 solution = -1
presolver terminated; took 1 ms
presolver terminated; took 3 ms
Parallelism: root=8, tree=10accept new sol: obj 0 bnd vio 0 int vio 0 mipgap inf time 0accept new sol: obj -42.8999996185303 bnd vio 0 int vio 0 mipgap 4.55011660905533 time 0
Model summary.- Num. variables : 48- Num. constraints : 15- Num. nonzeros : 96- Bound range : [1.0e+00,1.0e+00]- Objective range : [4.0e-01,9.8e+00]- Matrix range : [1.0e+00,1.0e+00]Presolver started.
Presolver terminated. Time : 0.002sSimplex method started.
Model fingerprint: ==gZ3Fmb392Y3JmZIteration Objective Dual Inf. Primal Inf. Time0 -2.38100e+02 0.0000e+00 8.1000e+01 0.03s 6 -4.29000e+01 0.0000e+00 0.0000e+00 0.03s
Postsolver started.
Simplex method terminated. Time : 0.007sRoot relaxation: -42.8999996185303 iteration = 6 time = 0.03
Branch-and-cut method terminated. Time : 0.548sOPTIMAL; objective 42.90Completed.Optimal obj is: 42.90
Optimal Matching X is
[[0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 1, 0, 0, 0, 0],[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 1, 0, 0]]
完整案例介绍:案例1:加权二分匹配(Weighted Bipartite Matching)
详细语法:向量化建模
结论:
MAPL作为一种先进的建模语言,通过支持向量和矩阵的声明以及丰富的运算操作符和映射函数,为用户处理多维数据提供了强大的工具集。无论是在学术研究还是工业应用中,MAPL的这些特点都显著地提高了数学建模的效率和便捷性。
相关文章:
MindOpt APL向量化建模语法的介绍与应用(2)
前言 在数据科学、工程优化和其他科学计算领域中,向量和矩阵的运算是核心组成部分。MAPL作为一种数学规划语言,为这些领域的专业人员提供了强大的工具,通过向量式和矩阵式变量声明以及丰富的内置数学运算支持,大大简化了数学建模…...

深入理解图形处理器(GPU):加速人工智能和大数据计算的引擎
文章目录 1. 什么是GPU?2. GPU的工作原理3. GPU的应用领域4. GPU与CPU的比较参考与推荐 前言: 图形处理器(GPU)不再仅仅是用于图形渲染的硬件设备。如今,GPU已经成为加速人工智能、大数据计算和科学研究的关键引擎。本…...

【Java探索之旅】数组使用 初探JVM内存布局
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java编程秘籍 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、数组的使用1.1 元素访问1.2 数组遍历 二、JVM的内存布局🌤️全篇总结 …...
RabbitMQ消息模型之Simple消息模型
simple消息模型 生产者 package com.example.demo02.mq.simple;import com.example.demo02.mq.util.ConnectionUtils; import com.rabbitmq.client.Channel; import com.rabbitmq.client.Connection;import java.io.IOException;/*** author Allen* 4/10/2024 8:07 PM* versi…...
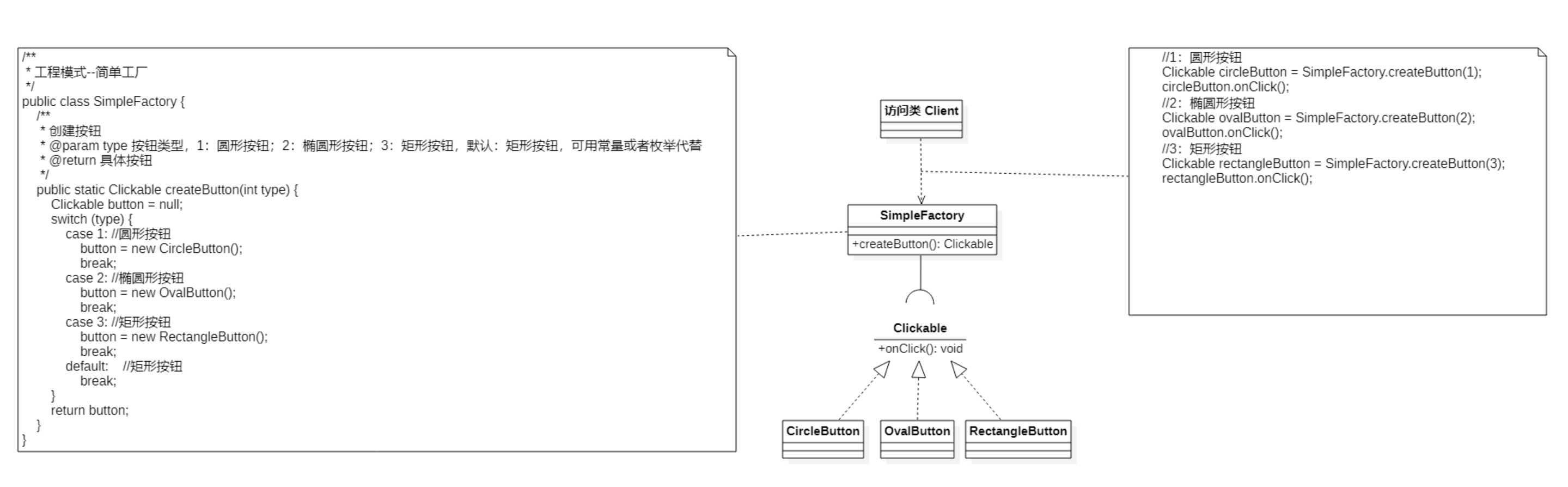
设计模式系列:简单工厂模式
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS二次开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 目录 定义 特点 使用场景 优缺点 (1) 优点…...

解决 windows+Ubuntu 时间不同步问题
本文所使用的 Ubuntu 系统版本是 Ubuntu 22.04 ! 如果你的电脑装了 Windows Ubuntu 系统,肯定会遇到时间不同步的问题。那么如何解决呢?参考步骤如下: # 步骤一:进入到 Ubuntu 系统# 步骤二:执行如下三条命令即可 sud…...
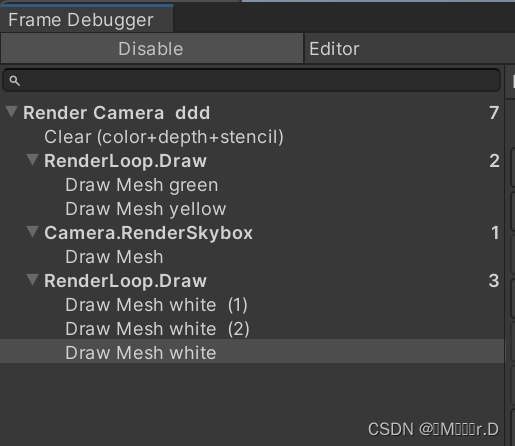
Learn SRP 01
学习链接:Custom Render Pipeline (catlikecoding.com) 使用Unity版本:Unity 2022.3.5f1 1.A new Render Pipeline 1.1Project Setup 创建一个默认的3D项目,项目打开后可以到默认的包管理器删掉所有不需要的包,我们只使用Unit…...
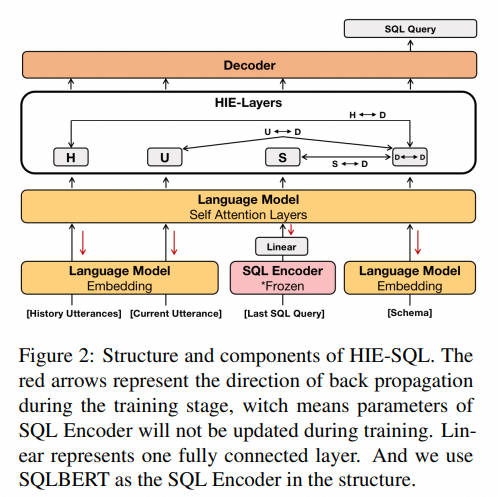
NL2SQL进阶系列(4):ConvAI、DIN-SQL、C3-浙大、DAIL-SQL-阿里等16个业界开源应用实践详解[Text2SQL]
NL2SQL进阶系列(4):ConvAI、DIN-SQL等16个业界开源应用实践详解[Text2SQL] NL2SQL基础系列(1):业界顶尖排行榜、权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2SQL、Text2DSL] NL2SQL基础系列(2):…...

Python统计分析库之statsmodels使用详解
概要 Python statsmodels是一个强大的统计分析库,提供了丰富的统计模型和数据处理功能,可用于数据分析、预测建模等多个领域。本文将介绍statsmodels库的安装、特性、基本功能、高级功能、实际应用场景等方面。 安装 安装statsmodels库非常简单,可以使用pip命令进行安装:…...
A Learning-Based Approach for IP Geolocation(2010年)
下载地址:Towards IP geolocation using delay and topology measurements | Proceedings of the 6th ACM SIGCOMM conference on Internet measurement 被引次数:185 Eriksson B, Barford P, Sommers J, et al. A learning-based approach for IP geolocation[C]//Passive …...
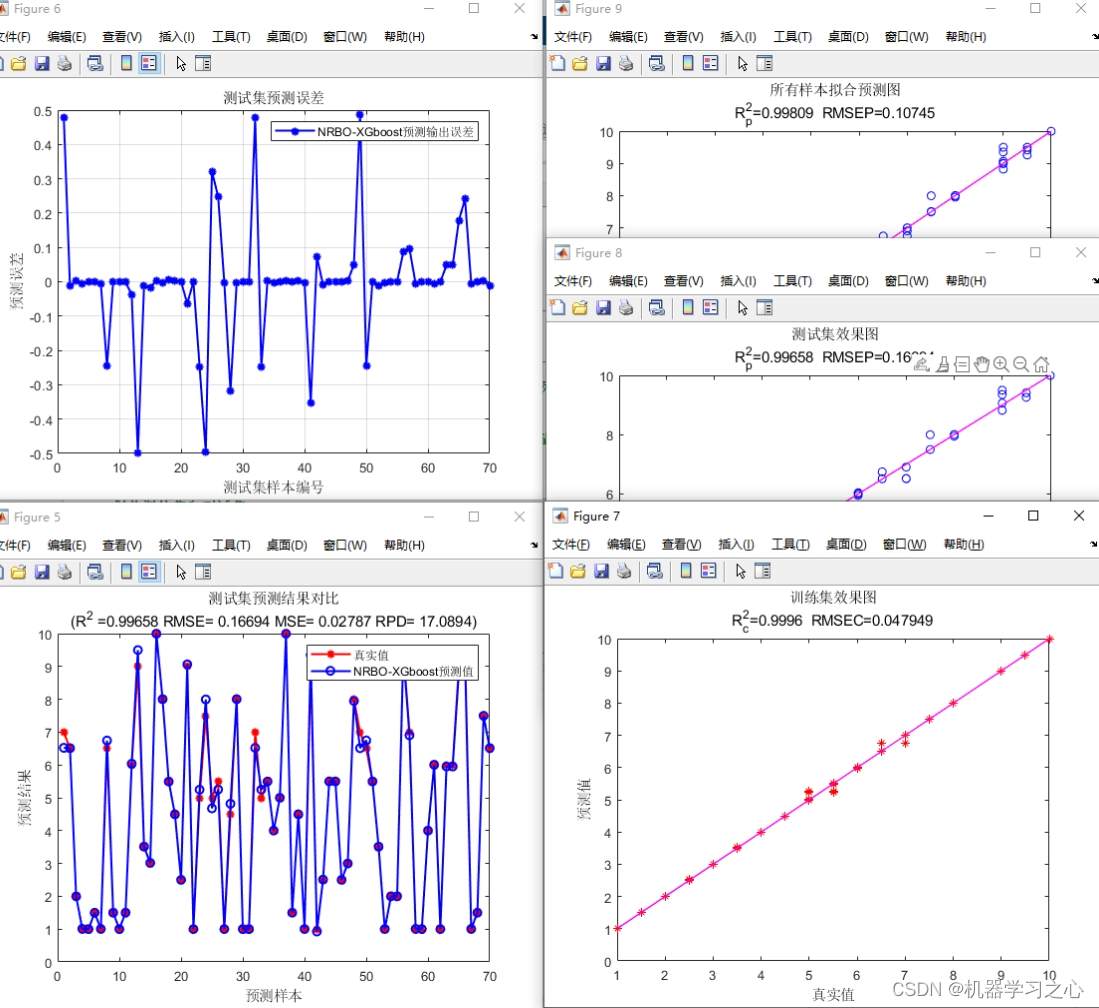
高创新 | [24年新算法]NRBO-XGBoost回归+交叉验证基于牛顿拉夫逊优化算法-XGBoost多变量回归预测
高创新 | [24年新算法]NRBO-XGBoost回归交叉验证基于牛顿拉夫逊优化算法-XGBoost多变量回归预测 目录 高创新 | [24年新算法]NRBO-XGBoost回归交叉验证基于牛顿拉夫逊优化算法-XGBoost多变量回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现 [24年新算…...

Web APP设计:将多个相近的机器学习模型融合到一个Web APP中
将多个相近的机器学习模型融合到一个Web APP中 FUSE-ML是一个用于预测腰椎融合术后效果的APP,它可以做出三个不同的结论,分别评价术后的腰痛、腿痛和日常功能是否提高。 这估计是部署了三个机器学习模型在这个APP中,因为一个机器学习模型仅…...

网络爬虫:定义、应用及法律道德考量
网络爬虫技术在当今数据驱动的世界中发挥着重要作用。本文将从网络爬虫的定义和主要功能,其在业界的应用实例,以及涉及的法律和道德问题三个方面进行深入探讨。 1. 爬虫的定义和主要功能 网络爬虫,也称为网页爬虫或蜘蛛,是一种…...
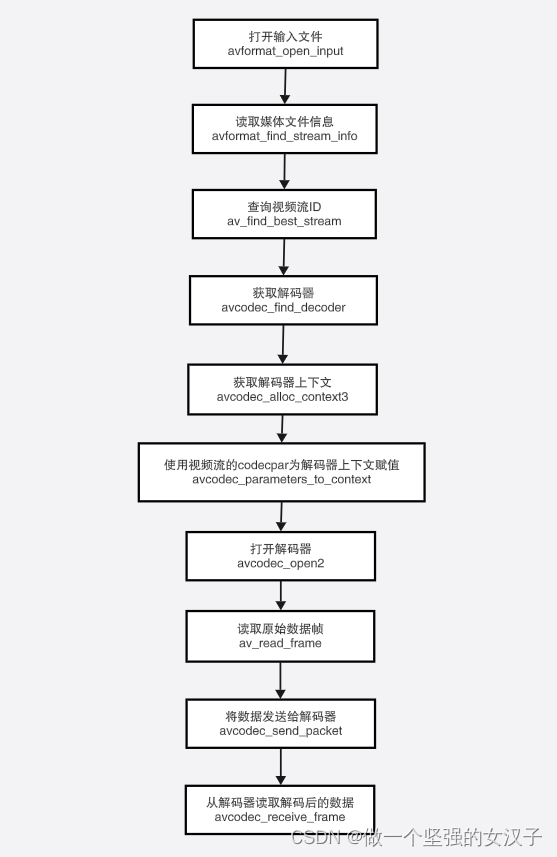
(三)ffmpeg 解码流程以及函数介绍
一、视频解码流程 二、函数介绍 1.avformat_network_init 函数作用: 执行网络库的全局初始化。这是可选的,不再推荐。 此函数仅用于解决旧GnuTLS或OpenSSL库的线程安全问题。如果libavformat链接到这些库的较新版本,或者不使用它们&#…...
go work模块与go mod包管理是的注意事项
如下图所示目录结构 cmd中是服务的包,显然auth,dbtables,pkg都是为cmd服务的。 首先需要需要将auth,dbtables,pkg定义到go.work中,如下: 在这样在各个单独的go mod管理的模块就可以互相调用了。一般情况下这些都是IDE自动进行的,…...
[100分])
华为OD-C卷-最长子字符串的长度(一)[100分]
题目描述 给你一个字符串 s,首尾相连成一个环形,请你在环中找出 o 字符出现了偶数次最长子字符串的长度。 输入描述 输入是一个小写字母组成的字符串 输出描述 输出是一个整数 备注 1 ≤ s.length ≤ 500000s 只包含小写英文字母用例1 输入 alolobo输出 6说明 最长子字…...
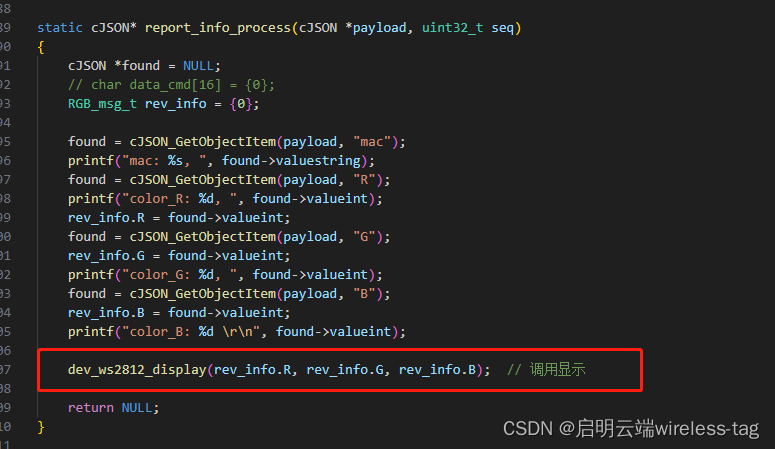
实战小项目 | ESP32-S3和ESP32-C3通过ESP-Mesh-Lite组网 温湿度传感器案例
传统Wi-Fi网络所有终端设备都需要直接与路由器相连,这使得Wi-Fi的覆盖区域受到路由器位置的限制,可接入终端设备的数量也受到路由器容量的限制。而乐鑫ESP-Mesh-Lite Wi-Fi组网方案,所有终端设备都可以与相邻设备连接,摆脱了对路由…...
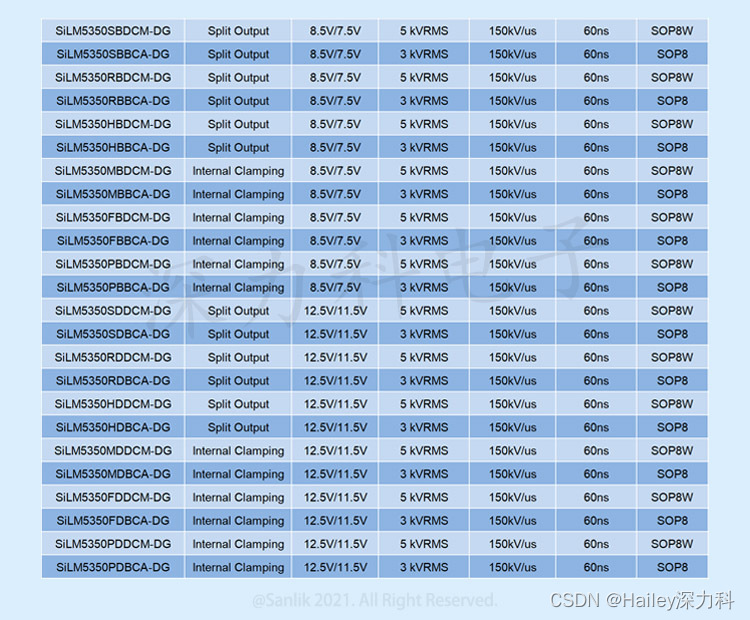
SiLM5350系列带米勒钳位的单通道隔离驱动器 助力汽车与工业应用实现稳定与高效的解决方案
带米勒钳位的隔离驱动SiLM5350系列 单通道 30V,10A 带米勒钳位的隔离驱动 具有驱动电流更大、传输延时更低、抗干扰能力更强、封装体积更小等优势, 为提高电源转换效率、安全性和可靠性提供理想之选。 SiLM5350系列产品描述: SiLM5350系列是单通道隔离驱…...

c#中怎么自动下载软件
以下是一个简单的 C# 示例,演示如何使用 WebClient 类下载软件: using System; using System.Net; class Program { static void Main(string[] args) { // 要下载的文件 URL string fileUrl "https://example.com/path/to/file"; // 本地保…...
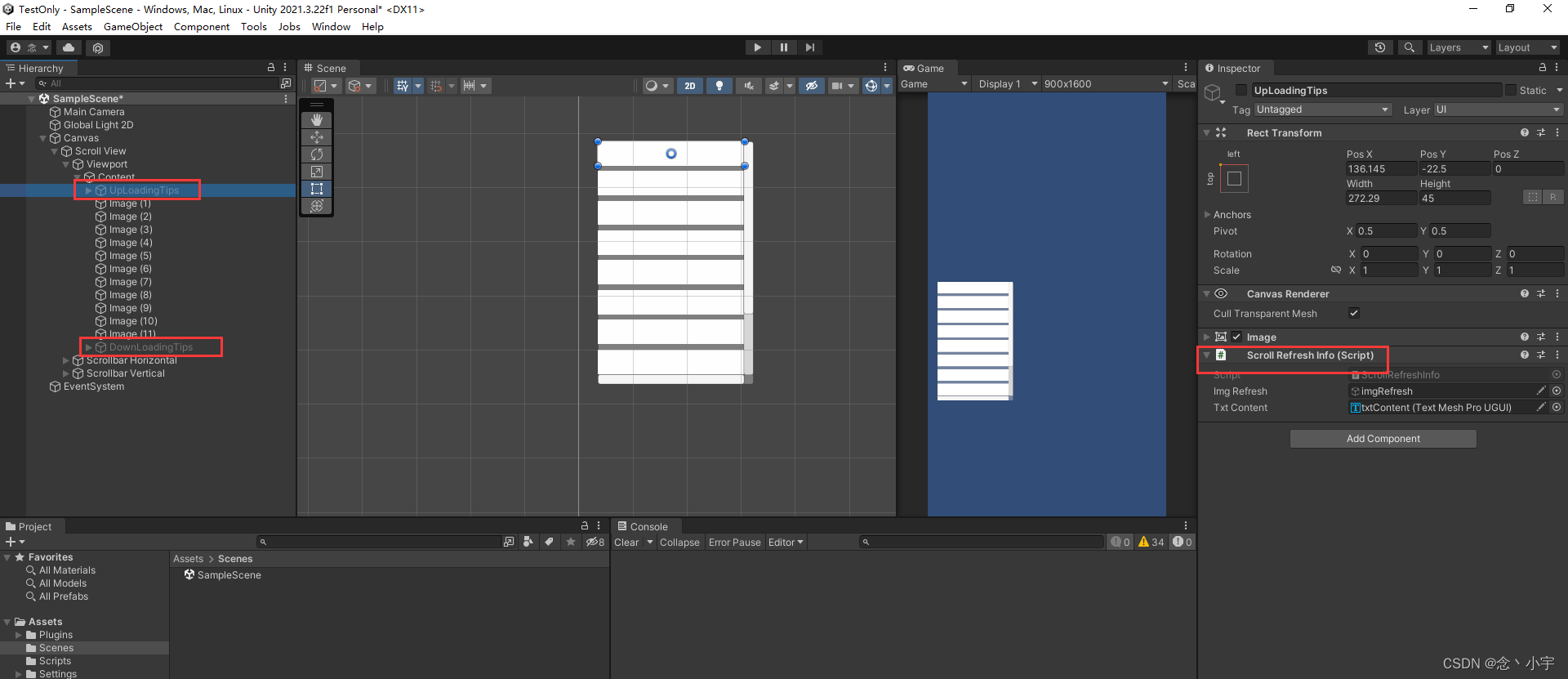
Unity笔记之下拉刷新列表
这样的效果; 代码: using System; using System.Collections; using System.Collections.Generic; using Sirenix.OdinInspector; using UnityEngine; using UnityEngine.EventSystems; using UnityEngine.UI;public class ScrollRectUpdateView : Mon…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
