《剑指 Offer》专项突破版 - 面试题 107 : 矩阵中的距离(C++ 实现)
题目链接:矩阵中的距离
题目:
输入一个由 0、1 组成的矩阵 M,请输出一个大小相同的矩阵 D,矩阵 D 中的每个格子是矩阵 M 中对应格子离最近的 0 的距离。水平或竖直方向相邻的两个格子的距离为 1。假设矩阵 M 中至少有一个 0。
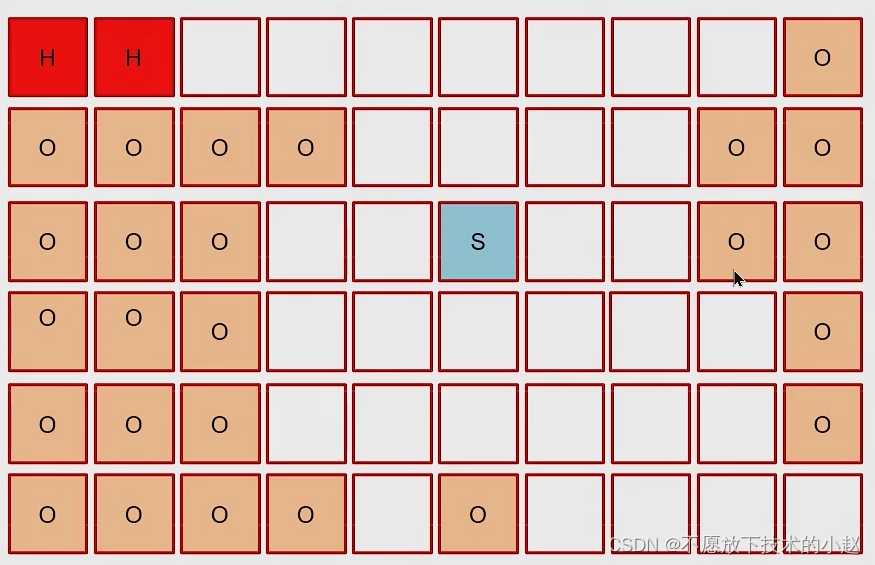
例如,下图 (a) 是一个只包含 0、1 的矩阵 M,它的每个格子离最近的 0 的距离如下图 (b) 的矩阵 D 所示。M[0][0] 等于 0,因此它离最近的 0 的距离是 0,所以 D[0][0] 等于 0。M[2][1] 等于 1,离它最近的 0 的坐标是 (0, 1)、(1, 0)、(1, 2),它们离坐标 (2, 1) 的距离都是 2,所以 D[2][1] 等于 2。

分析:
应用与图相关的算法解决问题的前提是能够找出图中的节点和边。这是一个背景为矩阵的问题,矩阵中的每个格子可以看成图中的一个节点,矩阵中上、下、左、右相邻的格子对应的节点之间有一条边相连。例如,可以将上图 (a) 中的矩阵看成下图所示的图。
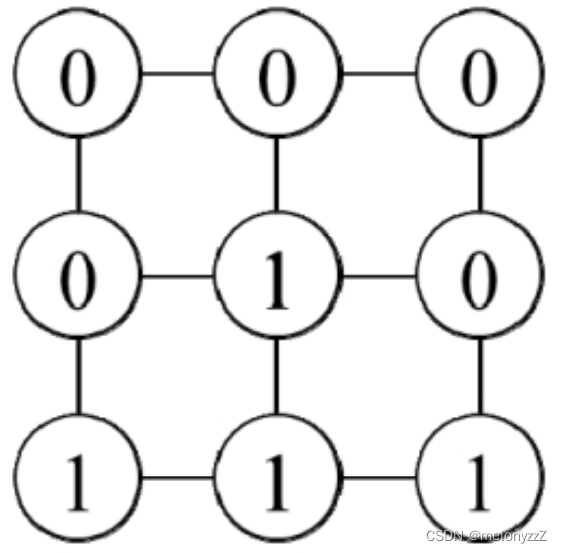
这个题目要求计算每个格子离最近的 0 的距离。根据题目的要求,上、下、左、右相邻的两个格子的距离为 1。可以将图看成一个无权图,图中两个节点的距离是连通它们的路径经过的边的数目。由于这个问题与无权图的最近距离相关,因此可以考虑应用广度优先搜索解决。
广度优先搜索需要一个队列。图中的哪些节点可以当作初始节点添加到队列中?这个问题是求每个格子离最近的 0 的距离,因此可以将所有的 0 当作初始节点添加到队列中,然后以值为 0 的节点作为起点做广度优先搜索。当经过 d 步到达某个格子,那么该格子离最近的 0 的距离就是 d。
class Solution {
public:vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int rows = mat.size(), cols = mat[0].size();vector<vector<int>> dists(rows, vector<int>(cols));
queue<vector<int>> q;for (int i = 0; i < rows; ++i){for (int j = 0; j < cols; ++j){if (mat[i][j] == 0){dists[i][j] = 0;q.push(vector<int>{ i, j });}else{dists[i][j] = INT_MAX;}}}
vector<vector<int>> dirs = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };while (!q.empty()){vector<int> coord = q.front();q.pop();int dist = dists[coord[0]][coord[1]];
for (vector<int>& dir : dirs){int r = coord[0] + dir[0];int c = coord[1] + dir[1];if (r >= 0 && r < rows && c >= 0 && c < cols){if (dists[r][c] > dist + 1){dists[r][c] = dist + 1;q.push(vector<int>{ r, c });}}}}return dists;}
};上述代码创建了一个大小与输入矩阵 mat 相同的二维数组 dists,用来记录每个格子离最近的 0 的距离。如果 mat[i][j] 为 0,那么这个格子离最近的 0 的距离自然是 0,因此 dists[i][j] 设为 0。如果 mat[i][j] 的值为 1,则先用最大的整数值初始化 dists[i][j],接下来搜索到对应的节点时再更新它的值。
队列中的元素是矩阵中格子的坐标,是一个长度为 2 的数组。一个格子的坐标被添加到队列中之前,它离最近的 0 的距离已经计算好并且保存在数组 dists 中。
每次从队列中取出一个坐标为 coord 的格子,该格子离最近的 0 的距离用变量 dist 表示。从该格子出发沿着上、下、左、右到达坐标为 (r, c) 的格子。如果该格子之前没有到达过,此时 dists[r][c] 的值仍然为最大的整数值,那么 dists[r][c] > dist + 1 的值为 true。由于是从离最近的 0 的距离为 dist 的格子多走一步到达该格子的,因此该格子离最近的 0 的距离是 dist + 1。此外,还需要将该格子添加到队列中,以便接下来搜索与该格子相连的其他节点。
如果之前已经到达坐标为 (r, c) 的格子,那么 dist[r][c] 的值一定不可能大于 dist + 1。这是因为用的是广度优先搜索,而广度优先搜索能够保证从起始节点到达任意节点一定是沿着最短路径的。当第 1 次到达坐标为 (r, c) 的格子时记录到 dists[r][c] 的值一定是从值为 0 的格子到达该格子的最短距离。因此,当再次到达坐标为 (r, c) 的格子时,dists[r][c] > dist + 1 的值为 false。通过比较距离可以避免重复访问某个格子。
相关文章:

《剑指 Offer》专项突破版 - 面试题 107 : 矩阵中的距离(C++ 实现)
题目链接:矩阵中的距离 题目: 输入一个由 0、1 组成的矩阵 M,请输出一个大小相同的矩阵 D,矩阵 D 中的每个格子是矩阵 M 中对应格子离最近的 0 的距离。水平或竖直方向相邻的两个格子的距离为 1。假设矩阵 M 中至少有一个 0。 …...

揭秘智慧礼品背后的故事
如若不是从事技术行业,在罗列礼品清单时,可能不会想到 “数据”,但幸运的是,我们想到了。如何将AI技术应用到当季一些最受青睐的产品中去,训练数据是这一智能技术的背后动力。很多电子设备或名称中带有“智能”一词的设…...

NVM的安装与配置
目录 一、简介二、下载2.1、windows环境下载地址2.2、安装 三、配置3.1、查看可安装版本3.2、安装版本3.3、使用和切换版本3.4、模块配置 四、其他4.1、全局安装pnpm4.2、常用nvm命令 一、简介 NVM,全称为Node Version Manager,是一个流行的命令行工具&a…...
[Java EE] 多线程(一) :线程的创建与常用方法(上)
1. 认识线程 1.1 概念 1.1.1 什么是线程 ⼀个线程就是⼀个"执⾏流".每个线程之间都可以按照顺序执⾏⾃⼰的代码.多个线程之间"同时"执⾏ 着多份代码. 还是回到我们之前的银⾏的例⼦中。之前我们主要描述的是个⼈业务,即⼀个⼈完全处理⾃⼰的…...
Linux安装docker(含Centos系统和Ubuntu系统)
一、Centos系统 1. 卸载旧版本依赖 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine 2. 设置仓库 安装所需的软件包。yum-utils 提供了 yum-config-manager &…...

【第十五届蓝桥杯大赛软件赛省赛】———— C/C++ 大学B组
蓝桥杯2024年15届省赛b组原题献上...

Redis+lua脚本限制ip多次输入错误密码
Redislua脚本限制ip多次输入错误密码 不能锁username,因为如果有人恶意保留破解密码的话。会导致用户本人无法登录。 这里我采用 以ip的方式进行锁定。利用redis 设置key:ip。value:当前ip尝试登录的次数 实现逻辑 逻辑简单,假设…...
全球顶级的低代码开发平台,你知道几个?
什么是低代码开发平台? 低码开发平台是一个应用程序,提供图形用户界面编程,从而以非常快的速度开发代码,减少了传统的编程工作。 这些工具有助于快速开发代码,最大限度地减少手工编码的努力。这些平台不仅有助于编码,而且还能快速安装和部署。 低码开发工具的好处 低代码平…...

11-1.Vue2.x基本列表—v-for
文章目录 Vue2.x基本列表—v-for Vue2.x基本列表—v-for <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><title>基本列表</title><script type"text/javascript" src"../js/vue.j…...

一本书精通推荐算法,轻松搞定入门、面试、进阶
当前互联网高速发展,用户规模和内容规模均迅猛提升。 身处信息严重过载的时代,如何让用户从海量信息中发现自己感兴趣的内容,成了很多公司的核心问题。 在此背景下,搜索系统和推荐系统应运而生。 前者主要解决用户主动寻找内容…...
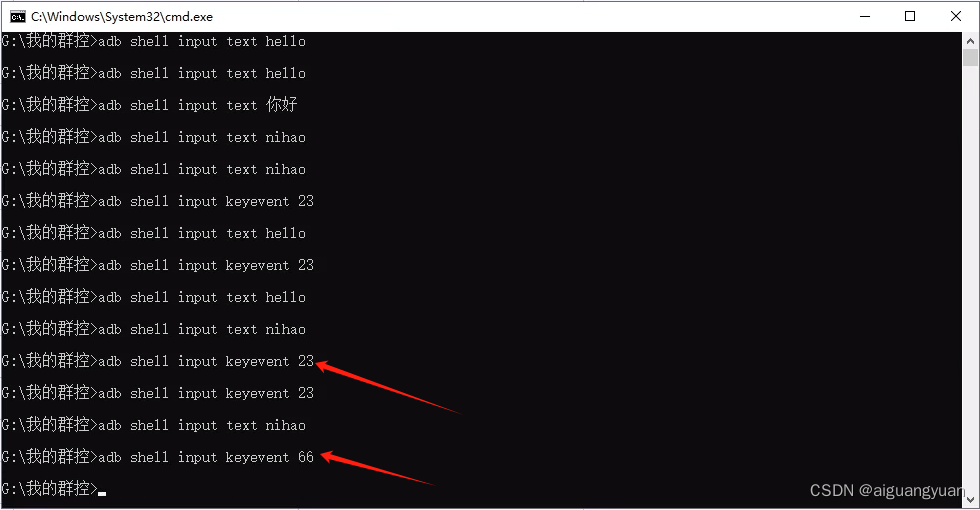
ADB的基本语法及常用命令
学习网址 ADB命令的基本语法如下: adb [-d|-e|-s <serialNumber>] <command> 如果有多个设备/模拟器连接,则需要为命令指定目标设备。 参数及含义如下: 常用命令如下: 1. 启动ADB服务 adb start-server 2. 停止…...

Linux之bpfjit(2)使用分析和mini-tcpdump实现
Linux之bpfjit(2)使用分析和mini-tcpdump实现 Author: Once Day Date: 2024年4月13日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可以参考专栏:…...

adb常用命令汇总
Android Debug Bridge (adb) 是一个多功能命令行工具,它允许你与连接的Android设备或在电脑上的Android模拟器进行通信。下面列出了一些常用的adb命令: 启动adb服务: adb start-server停止adb服务: adb kill-server查看已连接的设…...
JVM虚拟机(三)垃圾回收简介、垃圾回收算法、分代回收、垃圾回收器种类、G1垃圾回收器
目录 一、什么是垃圾回收?1.1 什么是垃圾回收?1.2 什么对象能被垃圾回收?1)引用计数法2)可达性分析算法 二、JVM 垃圾回收算法2.1 标记清除算法2.2 标记整理算法(标记压缩算法)2.3 复制算法2.4 …...
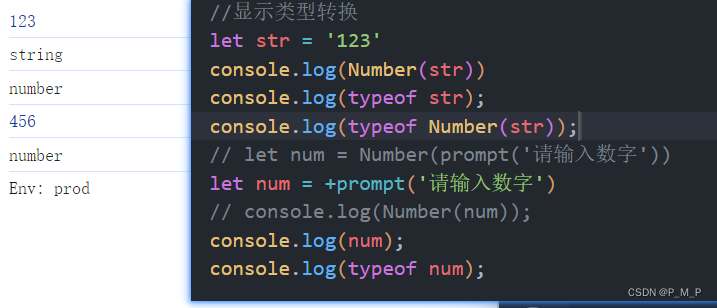
JavaScript基础:js介绍、变量、数据类型以及类型转换
目录 介绍 引入方式 内部方式 外部形式 注释和结束符 单行注释 多行注释 结束符 输入和输出 输出 输入 变量 声明 赋值 关键字 变量名命名规则 常量 数据类型 数值类型 字符串类型 布尔类型 undefined 类型转换 隐式转换 显式转换 Number ✨介绍 &a…...
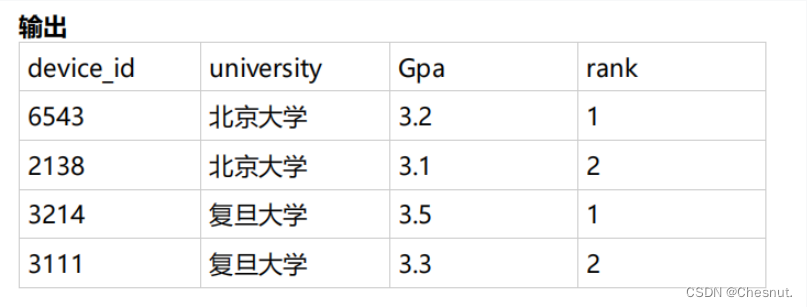
【牛客SQL快速入门】SQL基础(三)
一、条件函数 IF 条件函数 IF函数是最常用到的条件函数,写法为 if(xn,a,b),xn代表判断条件,如果xn时,那么结果返回a,否则返回b。 -- 把非北京大学的用户统一归为其他大学 Select device_id,if(university ‘北京大…...

Pytorch手撸Attention
Pytorch手撸Attention 注释写的很详细了,对照着公式比较下更好理解,可以参考一下知乎的文章 注意力机制 import torch import torch.nn as nn import torch.nn.functional as Fclass SelfAttention(nn.Module):def __init__(self, embed_size):super(S…...
PyCharm 2024.1 发布:全面升级,助力高效编程!
PyCharm 2024.1 发布:全面升级,助力高效编程! 文章目录 PyCharm 2024.1 发布:全面升级,助力高效编程!摘要引言 Hugging Face:模型和数据集的快速文档预览针对 JavaScript 和 TypeScript 的全行代…...
)
Nginx基础(06)
Nginx基础(05) uWSGI 介绍 uWSGI 是一个 Web服务器 主要用途是将Web应用程序部署到生产环境中 可以用来连接Nginx服务与Python动态网站 1. 用 uWSGI 部署 Python 网站项目 配置 Nginx 使其可以将动态访问转交给 uWSGI 安装 python 工具及依赖 安…...

【Qt 学习笔记】QWidget的windowOpacity属性 | cursor属性 | font属性
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ QWidget的windowOpacity属性 | cursor属性 | font属性 文章编号&#…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
