Java——二叉树
二叉树
二叉树在Java中是一种重要的数据结构,用于高效地组织和处理具有层级关系的数据。
二叉树的每个节点最多有两个子节点,这两个子节点分别称为左子节点和右子节点。这种结构非常适合于使用递归的方式进行定义和操作。在计算机科学中,二叉树可以用于多种算法和应用,如排序、搜索以及作为其他复杂数据结构如堆、红黑树等的基础。
下面是关于二叉树的一些重要概念:
- 基本定义:二叉树是节点的集合,可以是空集或由一个根节点和两棵互不相交的左右子树组成。
- 特殊类型:有满二叉树和完全二叉树等特殊形式,它们在特定条件下拥有最优的存储和操作效率。
- 性质:二叉树的第i层最多有2^(i-1)个节点,深度为k的二叉树至多有2^k - 1个节点。
- 操作:二叉树可以有多种操作,包括不同方式的遍历(前序、中序、后序),查找特定值的节点,以及计算二叉树的高度等。
- 应用:二叉树常应用于文件系统、排序算法和内存管理等领域。
- 实现:在Java中,可以通过创建一个包含左右子节点引用的TreeNode类来表示二叉树的节点。然后可以通过创建TreeNode对象并设置它们的链接来构建整个二叉树结构。
以下是一个简单的Java二叉树节点类的示例:
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }
}
在这个类中,val变量用于存储节点的值,left和right变量分别指向左子节点和右子节点。
要创建一个二叉树,我们可以手动创建节点并将它们链接起来,或者使用递归方法自动创建。以下是一个简单的递归创建二叉树的示例:
public TreeNode createBinaryTree(int[] values, int index) {if (index >= values.length || values[index] == -1) {return null;}TreeNode node = new TreeNode(values[index]);node.left = createBinaryTree(values, 2 * index + 1);node.right = createBinaryTree(values, 2 * index + 2);return node;
}
在这个函数中,我们首先检查索引是否超出数组的范围或者当前值是否为-1(表示空节点),如果是则返回null。然后我们创建一个新的节点,并递归地为其左子节点和右子节点赋值。
二叉树有许多重要的操作,如遍历、查找和插入等。以下是一个简单的前序遍历二叉树的示例:
public void preorderTraversal(TreeNode node) {if (node == null) {return;}System.out.print(node.val + " ");preorderTraversal(node.left);preorderTraversal(node.right);
}
在这个函数中,我们首先打印当前节点的值,然后递归地遍历左子树和右子树。这就是前序遍历的基本思想。
二叉排序树
Java中的二叉排序树是一种特殊的二叉树,它具有明确的排序性质。以下是关于二叉排序树的一些关键点:
- 定义和性质:二叉排序树(BST)是具有以下特性的二叉树,对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,其右子树中的所有节点的值都大于该节点的值。这种性质保证了二叉排序树在查找、插入和删除等操作上具有较高的效率。
- 创建和遍历:可以通过插入操作逐个添加节点来创建二叉排序树。遍历方式包括前序遍历、中序遍历和后序遍历,其中中序遍历可以得到树中所有元素的升序排列。
- 实现细节:在Java中实现二叉排序树时,通常定义一个包含元素值以及指向左右子节点引用的Node类。通过维护二叉排序树的性质,可以确保树在执行各种操作时保持正确的结构。
- 实际应用:由于二叉排序树具有快速检索的特点,它们常被用于数据库索引、有序集合等数据结构中,以提供高效的数据检索和管理功能。
- 注意事项:在处理二叉排序树时需要注意,如果插入的数据违反了二叉排序树的定义,那么树的结构将不会被正确维护。因此,插入和删除操作必须谨慎执行,以确保树的排序性质不被破坏。
以下是一个简单的Java二叉排序树实现示例:
public class BinarySortTree {private Node root;private static class Node {int value;Node left;Node right;public Node(int value) {this.value = value;}}public void insert(int value) {root = insert(root, value);}private Node insert(Node node, int value) {if (node == null) {return new Node(value);}if (value < node.value) {node.left = insert(node.left, value);} else if (value > node.value) {node.right = insert(node.right, value);}return node;}public boolean contains(int value) {return contains(root, value);}private boolean contains(Node node, int value) {if (node == null) {return false;}if (value < node.value) {return contains(node.left, value);} else if (value > node.value) {return contains(node.right, value);} else {return true;}}public void remove(int value) {root = remove(root, value);}private Node remove(Node node, int value) {if (node == null) {return null;}if (value < node.value) {node.left = remove(node.left, value);} else if (value > node.value) {node.right = remove(node.right, value);} else {if (node.left == null) {return node.right;} else if (node.right == null) {return node.left;}node.value = minValue(node.right);node.right = remove(node.right, node.value);}return node;}private int minValue(Node node) {int minValue = node.value;while (node.left != null) {minValue = node.left.value;node = node.left;}return minValue;}
}
在这个示例中,我们定义了一个BinarySortTree类,它包含一个根节点root和一个内部类Node。Node类表示二叉排序树的节点,包含一个整数值、一个左子节点和一个右子节点。BinarySortTree类提供了插入、查找和删除等基本操作的方法。
平衡二叉树
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉搜索树,它的每个节点的左子树和右子树的高度差不超过1。这种数据结构可以保证在插入、删除和查找操作时具有较高的效率,时间复杂度为O(log n)。
在Java中,可以使用AVL树(一种自平衡二叉搜索树)来实现平衡二叉树。AVL树是一种高度平衡的二叉搜索树,它在每次插入或删除节点后,都会通过旋转操作来保持树的平衡。
AVL树的基本操作包括:
- 插入(Insert):向AVL树中插入一个新的键值。
- 删除(Delete):从AVL树中删除一个键值。
- 查找(Search):在AVL树中查找一个指定的键值。
- 旋转(Rotate):通过旋转操作来保持树的平衡。
AVL树的主要优点是在保持平衡的同时,还能保持二叉搜索树的性质,因此在查找、插入和删除操作时具有较高的效率。但是,由于需要维护平衡,AVL树的实现相对复杂。
如何保持平衡
AVL树通过在每个节点上维护一个平衡因子来保持平衡。平衡因子是该节点的左子树的高度与右子树的高度之差。平衡因子可以是 -1、0 或 1,这确保了每个节点的左右子树的高度差不会超过 1,从而维持了树的平衡状态。
当执行插入或删除操作时,AVL树会检查每个受影响节点的平衡因子。如果任何节点的平衡因子变为非法值(即不是 -1、0 或 1),则会进行一系列旋转来恢复平衡。这些旋转操作包括:
单旋转:当一个节点的平衡因子变为非法值时,如果不平衡在节点的某一侧,那么只需要一次旋转就可以恢复平衡。这又分为:
- 右旋:如果节点的左子树高度大于右子树,需要进行右旋。
- 左旋:如果节点的右子树高度大于左子树,需要进行左旋。
双旋转:如果不平衡在节点的两侧,可能需要两次旋转来恢复平衡。这又分为:
- 左右旋:首先对节点的左孩子进行左旋,然后对节点进行右旋。
- 右左旋:首先对节点的右孩子进行右旋,然后对节点进行左旋。
通过这些旋转操作,AVL树可以在每次插入或删除后保持平衡,确保了操作的时间复杂度保持在 O(log n)。
总结来说,AVL树通过以下方式保持平衡:
- 维护每个节点的平衡因子。
- 在插入和删除操作后检查并更新平衡因子。
- 如果检测到不平衡,使用旋转操作来重新平衡。
代码示例
class Node {int key, height;Node left, right;Node(int d) {key = d;height = 1;}
}class AVLTree {Node root;int height(Node N) {if (N == null)return 0;return N.height;}int max(int a, int b) {return (a > b) ? a : b;}Node rightRotate(Node y) {Node x = y.left;Node T2 = x.right;x.right = y;y.left = T2;y.height = max(height(y.left), height(y.right)) + 1;x.height = max(height(x.left), height(x.right)) + 1;return x;}Node leftRotate(Node x) {Node y = x.right;Node T2 = y.left;y.left = x;x.right = T2;x.height = max(height(x.left), height(x.right)) + 1;y.height = max(height(y.left), height(y.right)) + 1;return y;}int getBalance(Node N) {if (N == null)return 0;return height(N.left) - height(N.right);}Node insert(Node node, int key) {if (node == null)return (new Node(key));if (key < node.key)node.left = insert(node.left, key);else if (key > node.key)node.right = insert(node.right, key);elsereturn node;node.height = 1 + max(height(node.left), height(node.right));int balance = getBalance(node);if (balance > 1 && key < node.left.key)return rightRotate(node);if (balance < -1 && key > node.right.key)return leftRotate(node);if (balance > 1 && key > node.left.key) {node.left = leftRotate(node.left);return rightRotate(node);}if (balance < -1 && key < node.right.key) {node.right = rightRotate(node.right);return leftRotate(node);}return node;}
}
红黑树
Java中的红黑树是一种自平衡的二叉查找树,它通过颜色和结构规则来保持树的平衡。
红黑树是一种特殊的二叉查找树,它的每个节点都有一个颜色属性,要么是红色,要么是黑色。红黑树需要满足以下条件:
- 节点颜色:每个节点要么是红色,要么是黑色。
- 根节点是黑色:树的根节点必须是黑色。
- 叶子节点是黑色:所有叶子节点(NIL节点,空节点)都是黑色。
- 红色节点的规则:如果一个节点是红色,那么它的两个子节点都必须是黑色。
- 路径上的黑色节点数量:从任一节点到其后代叶子的所有路径上包含相同数目的黑节点。
当进行插入或删除操作时,可能会破坏上述规则,此时需要通过旋转和重新着色来修复,以确保树继续保持平衡。旋转分为左旋和右旋,用于改变树的结构;重新着色则是改变某些节点的颜色,以符合红黑树的规则。
public class RedBlackTree {private static final boolean RED = true;private static final boolean BLACK = false;private class Node {int key;Node left, right, parent;boolean color;Node(int key) {this.key = key;this.color = RED;}}private Node root;public void insert(int key) {Node newNode = new Node(key);if (root == null) {root = newNode;root.color = BLACK;} else {Node current = root;Node parent;while (true) {parent = current;if (key < current.key) {current = current.left;if (current == null) {parent.left = newNode;newNode.parent = parent;break;}} else {current = current.right;if (current == null) {parent.right = newNode;newNode.parent = parent;break;}}}fixInsert(newNode);}}private void fixInsert(Node node) {while (node != root && node.parent.color == RED) {if (node.parent == node.parent.parent.left) {Node uncle = node.parent.parent.right;if (uncle != null && uncle.color == RED) {node.parent.color = BLACK;uncle.color = BLACK;node.parent.parent.color = RED;node = node.parent.parent;} else {if (node == node.parent.right) {node = node.parent;rotateLeft(node);}node.parent.color = BLACK;node.parent.parent.color = RED;rotateRight(node.parent.parent);}} else {Node uncle = node.parent.parent.left;if (uncle != null && uncle.color == RED) {node.parent.color = BLACK;uncle.color = BLACK;node.parent.parent.color = RED;node = node.parent.parent;} else {if (node == node.parent.left) {node = node.parent;rotateRight(node);}node.parent.color = BLACK;node.parent.parent.color = RED;rotateLeft(node.parent.parent);}}}root.color = BLACK;}private void rotateLeft(Node node) {Node temp = node.right;node.right = temp.left;if (temp.left != null) {temp.left.parent = node;}temp.parent = node.parent;if (node.parent == null) {root = temp;} else if (node == node.parent.left) {node.parent.left = temp;} else {node.parent.right = temp;}temp.left = node;node.parent = temp;}private void rotateRight(Node node) {Node temp = node.left;node.left = temp.right;if (temp.right != null) {temp.right.parent = node;}temp.parent = node.parent;if (node.parent == null) {root = temp;} else if (node == node.parent.right) {node.parent.right = temp;} else {node.parent.left = temp;}temp.right = node;node.parent = temp;}
}
相关文章:

Java——二叉树
二叉树 二叉树在Java中是一种重要的数据结构,用于高效地组织和处理具有层级关系的数据。 二叉树的每个节点最多有两个子节点,这两个子节点分别称为左子节点和右子节点。这种结构非常适合于使用递归的方式进行定义和操作。在计算机科学中,二…...

数据仓库—维度建模—事实表设计
事实表 事实表是数据仓库中的核心表,用于记录与业务过程相关的事实信息,是进行数据分析和挖掘的主要数据来源。 在ER模型中抽象出了有实体、关系、属性三种类别,在现实世界中,每一个操作型事件,基本都是发生在实体之间的,伴随着这种操作事件的发生,会产生可度量的值,…...

《系统架构设计师教程(第2版)》第9章-软件可靠性基础知识-05-软件可靠性测试
文章目录 1. 概述2. 定义软件运行剖面2.1 软件的使用行为建模2.2 输入域分层2.3 弧上的概率分配2.4 其他注意点 3. 可靠性测试用例设计4. 可靠性测试的实施4.1 测试前检查4.2 注意点4.2 可靠性测试的难点1)失效判断的主观性2)计算的错误结果不易被发现 4…...

uni-app vue3 setup 如何使用 onShow
在uni-app中,onShow是uni.onAppShow的别名,用于监听当前小程序被用户切换到前台运行时触发。在Vue 3中,你可以通过以下方式使用onShow: 在页面的vue文件中添加onShow方法: javascript <button click“onShow”&g…...
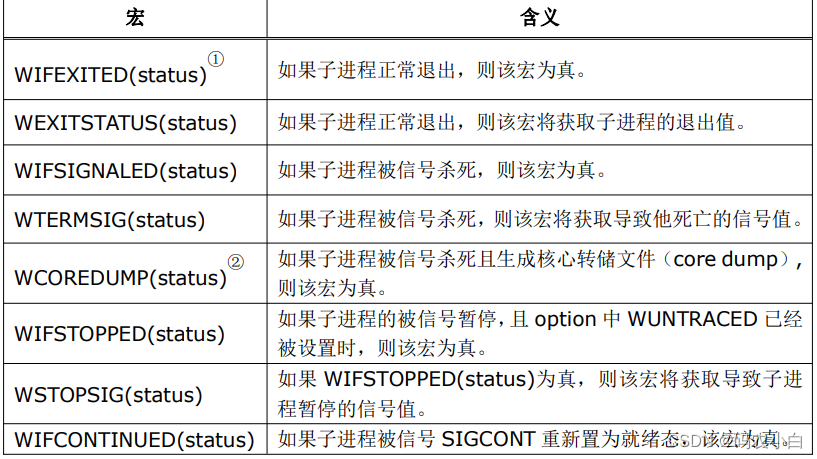
linux学习:进程(新建+运行某文件+退出处理函数+等待)
目录 api 创建新进程 注意 运行某文件 例子 注意 例子,等待进程 进程是由进程控制块、程序段、数据段三部分组成 进程有都有一个父进程,除了init,父进程可以创建子进程 每个进程都有一个PID,可以用ps来查看,等…...
Leetcode. 12 整数转罗马数字
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例…...

【uniapp】request请求函数封装,token、成功、失败等
1、封装http.ts //utils--->http.ts/*** 添加拦截器* 拦截request请求* 拦截uploadFile文件上传** TODO* 1、非http开头需要拼接地址* 2、请求超时* 3、添加小程序端请求头标识* 4、添加token请求头标识*/ import { useMemberStore } from /stores/index const member…...
0基础如何入门编程?
0基础如何进入IT行业 ? 前言 简介:对于没有任何相关背景知识的人来说,如何才能成功进入IT行业?是否有一些特定的方法或技巧可以帮助他们实现这一目标? 主要方法有如下几点建议提供给宝子们 目录 免费视频网课学习…...
Go 单元测试基本介绍
文章目录 引入一、单元测试基本介绍1.1 什么是单元测试?1.2 如何写好单元测试1.3 单元测试的优点1.4 单元测试的设计原则 二、Go语言测试2.1 Go单元测试概要2.2 Go单元测试基本规范2.3 一个简单例子2.3.1 使用Goland 生成测试文件2.3.2 运行单元测试2.3.3 完善测试用…...
uniapp 上传视频到阿里云之后回显视频获取视频封面
uniapp 上传视频到阿里云之后回显视频获取视频封面 官网的解决方案 1.initial-time Number 指定视频初始播放位置,单位为秒(s)。 没什么卵用 2.使用 uni.createVideoContext(“myVideo”, this).seek(number)。 没什么卵用 <video :id&quo…...
使用undetected-chromedriver遇到的问题及解决方法,以及它使用SOCKS代理的问题
环境:python3.8.10 uc的安装方法: pip38 install undetected-chromedriver 上测试代码: import undetected_chromedriver as uc driver uc.Chrome() driver.get(https://www.baidu.com) driver.save_screenshot(baidu.png)报错ÿ…...

Hadoop入门学习路线
目录 一、基础理论学习 二、安装与配置 三、Hadoop安装与部署 四、实践操作与项目练习 五、进阶学习 六、学习资源推荐 一、基础理论学习 了解Hadoop的起源、发展历程及其在大数据领域的重要性。 掌握Hadoop的核心组件及其作用,包括HDFS(分布式文件…...
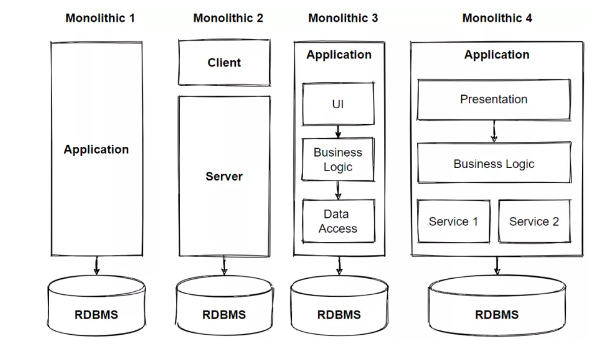
Python中的设计模式与最佳实践【第166篇—设计模式】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 Python中的设计模式与最佳实践 在软件开发中,设计模式是一种解决常见问题的经过…...

Python赋能AI数据分析开启人工智能新时代
文章目录 一、Python是办公自动化的重要工具二、Python是提升职场竞争力的利器三、Python是企业数字化的重要平台四、Python是AI发展的重要通道之一《编程菜鸟学Python数据分析》编辑推荐内容简介作者简介目录前言为什么要写这本书读者对象如何阅读本书 随着我国企业数字化和信…...

TP5使用group报错:1055 Expression #1 of SELECT list is not in GROUP
使用group报错 Mysql环境是5.7的, 使用了View进行了表连接, 进行了表连接 搬迁到本地后, 查询报错 Syntax error or access violation: 1055 Expression 解决方法1 配置 my.cnf(linux)文件 win下面是 mysql.ini文件 在 mysqld 里加上 sql_modeNO_ENGINE_SUBSTITUTION,STR…...
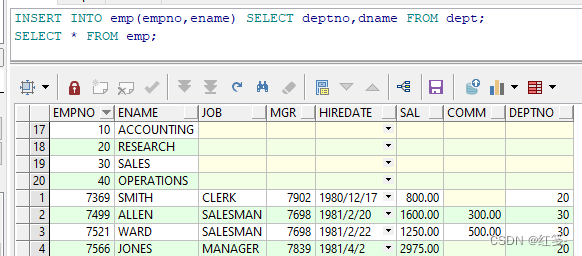
SQL-DML数据操纵语言(Oracle)
文章目录 DML数据操纵语言常见的字段属性字符型字段属性char(n)varchar2(n)/varchar(n) 数值型字段属性number([p],[s]int 日期型字段属性DATEtimestamp 如何查看字段属性增加数据INSERT快捷插入 删除数据DELETE修改数据UPDATE DML数据操纵语言 定义 是针对数据做处理…...

springboot+axios传参问题
目录 get请求方式: 不携带参数: 携带参数 第一种方式: 第二种传参方式: post方式: 携带参数: 第一种方式: 第二种方式:...
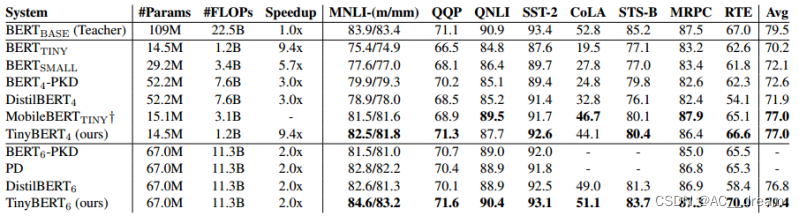
(BERT蒸馏)TinyBERT: Distilling BERT for Natural Language Understanding
文章链接:https://arxiv.org/abs/1909.10351 背景 在自然语言处理(NLP)领域,预训练语言模型(如BERT)通过大规模的数据训练,已在多种NLP任务中取得了卓越的性能。尽管BERT模型在语言理解和生成…...

【数据结构|C语言版】双向链表
前言1. 初步认识双向链表1.1 定义1.2 结构1.3 储存 2. 双向链表的方法(接口函数)2.1 动态申请空间2.2 创建哨兵位2.3 查找指定数据2.4 指定位置插入2.5 指定位置删除2.6 头部插入2.7 头部删除2.8 尾部插入2.9 尾部删除2.10 计算链表大小2.11 销毁链表 3.…...
适用于 Windows 的 10 个顶级 PDF 编辑器 [免费和付费]
曾经打开PDF文件,感觉自己被困在数字迷宫中吗?无法编辑的文本、无法调整大小的图像以及签署感觉像是一件苦差事的文档?好吧,不用再担心了!本指南解开了在 Windows 上掌握 PDF 的秘密,其中包含 10 款适用于 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
