DP4 最小花费爬楼梯
原题链接:最小花费爬楼梯_牛客题霸_牛客网
目录
1. 题目描述
2. 思路分析
3. 代码实现
1. 题目描述
2. 思路分析
dp。
开一个dp数组和a数组。dp[i]表示在当前这一格所需要的费用,a数组其实就是题目中的cost数组。
因为最后要求到顶楼的最低费用,每次只能走一格或走两格,所以我们要求走一格到当前格的费用和走两个到当前格的费用的最小值。
在第0格和第1格时不需要费用。
初始状态: dp[0]=0 dp[1]=0
状态转移方程:dp[i]=min(dp[i-2]+a[i-2],dp[i-1]+a[i-1])
最终状态 dp[n]
3. 代码实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N=1e5+10;
int a[N],dp[N];signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n; cin>>n;for(int i=0;i<n;i++) cin>>a[i];dp[0]=0;dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-2]+a[i-2],dp[i-1]+a[i-1]);}cout<<dp[n]<<endl;
}相关文章:

DP4 最小花费爬楼梯
原题链接:最小花费爬楼梯_牛客题霸_牛客网 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 dp。 开一个dp数组和a数组。dp[i]表示在当前这一格所需要的费用,a数组其实就是题目中的cost数组。 因为最后要求到顶楼的最低费用&a…...

OpenXR API概览与核心组件解析
在虚拟现实(VR)和增强现实(AR)领域,OpenXR API提供了一个重要的开放标准,使得开发者能够跨多种硬件和软件平台创建兼容的应用。本文将详细解释OpenXR中的核心组件和数据结构,并探讨它们如何共同…...
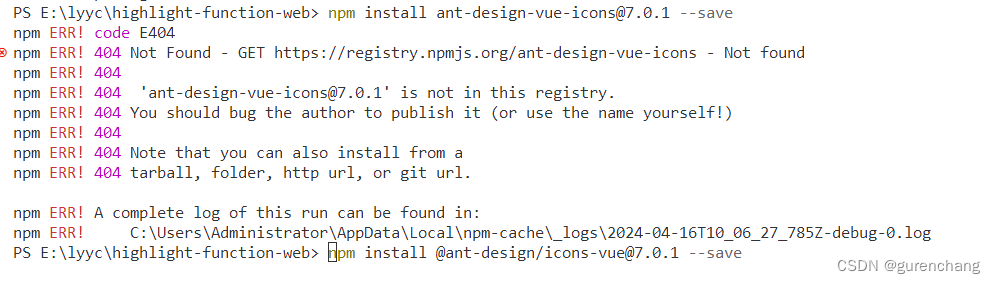
安装指定版本的ant-design-vue和指定版本的@ant-design/icons-vue 图标组件包
前言: 最近在完成公司的项目时,为了兼容其他的版本,需要安装指定版本的ant-design-vue和ant-design/icons-vue 图标组件包,安装成功之后,分享如下: 安装命令: ant-design-vue: 不…...

Zynq7000系列中的休眠模式
休眠模式是在系统层面定义的,它包括将APU置于待机模式,并将多个控制器保持在无时钟的复位状态。 进入休眠模式可以大大降低功耗。在休眠模式下,大多数功能时钟组都会被关闭或断电。唯一需要保持活动的设备是一个CPU、窥探控制单元(…...

在redhat7/8平台上部署ELK7.17.18的技术方案
部署环境说明 为节省资源直接使用1台测试机模拟3节点elasticsearch服务集群做部署,在该主机上同时部署了3个elasticsearch实例、1个logstash实例、1个kibana实例、1个filebeat实例。对于生产环境,以上实例服务应该做分布式部署。 ELK-TEST1 192.168.10…...
分享6个好用的ChatGPT)
(Chat For Al,创新Al,汇语Al助手,AiTab新标签,万能助手,LLaVA)分享6个好用的ChatGPT
目录 1、Chat For AI 2、创想AI 3、汇语AL助手...

MySQL-锁篇
文章目录 表级锁和行级锁了解吗?有什么区别?行级锁使用有什么注意事项?InnoDB有哪几类行锁?共享锁和排他锁是什么?意向锁有什么用? 锁是一种常见的并发事务的控制方式 表级锁和行级锁了解吗?有什…...

滤波器笔记(杂乱)
线性相位是时间平移,相位不失真 零、基础知识 1、用相量表示正弦量 https://zhuanlan.zhihu.com/p/345546880 https://www.zhihu.com/question/347763932/answer/1103938667 A s i n ( ω t θ ) ⇔ A e j θ ⇔ A ∠ θ Asin(\omega t\theta) {\Leftrightarrow…...
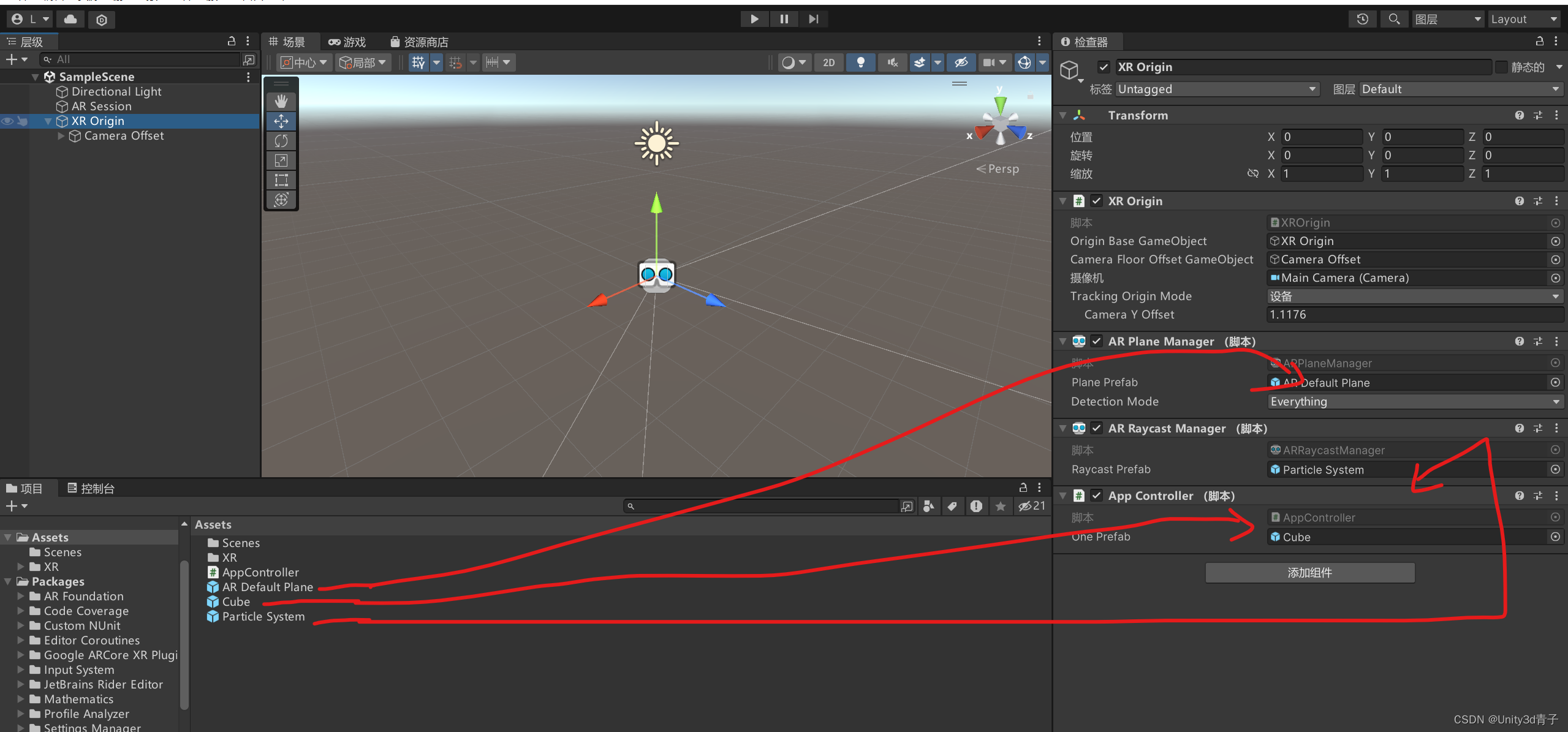
【ARFoundation自学01】搭建AR框架,检测平面点击位置克隆物体
Unity开发ARFoundation相关应用首先安装ARFoundation包 然后设置XR 1.基础AR场景框架搭建 2.一个基本的点击克隆物体到识别的平面脚本 挂在XROrigin上 脚本AppController 脚本说明书 ## 业务逻辑 AppController 脚本旨在实现一个基本的 AR 应用程序功能:用户通过…...

.Net ajax 接收参数
后端部分代码 一般处理程序 public void ProcessRequest(HttpContext context){context.Response.ContentType "text/plain";string str_index context.Request.Form.AllKeys.Contains("index") ? context.Request.Form["index"].ToString(…...

智能零售:引领购物新时代
智能零售通过整合人工智能、物联网、大数据和机器学习等技术,正在彻底改变传统的购物模式,为消费者和零售商提供前所未有的效率和个性化体验。 智能零售利用消费者数据分析来提供个性化的购物推荐。无论是在线平台或是实体店内,智能系统都能…...

【AIGC】AIGC在虚拟数字人中的应用:塑造未来互动体验的革新力量
🚀 🚀 🚀随着科技的快速发展,AIGC已经成为引领未来的重要力量。其中,AIGC在虚拟数字人领域的应用更是引起了广泛关注。虚拟数字人作为一种先进的数字化表达形式,结合了3D建模、动画技术、人工智能等多种先进…...

电机控制器电路板布局布线参考指导(五)
电机控制器电路板布局布线参考指导(五)大容量电容和旁路电容的放置 1.大容量电容的放置2.电荷泵电容器3.旁路电容/去耦电容的放置3.1 靠近电源3.2 靠近功率器件3.3 靠近开关电流源3.4 靠近电流感测放大器3.5 靠近稳压器 tips:资料主要来自网络…...

Python医院挂号脚本
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。 会一些的技术:数据分析、算法、SQL、大数据相关、python 欢迎加入社区:码上找工作 作者专栏每日更新: LeetCode解锁1000题: 打怪升级之旅 python数据分析…...
LabVIEW光学探测器板级检测系统
LabVIEW光学探测器板级检测系统 特种车辆乘员舱的灭火抑爆系统广泛采用光学探测技术来探测火情。光学探测器作为系统的关键部件,其探测灵敏度、响应速度和准确性直接关系到整个系统的运行效率和安全性。然而,光学探测器在长期使用过程中可能会因为灰尘污…...
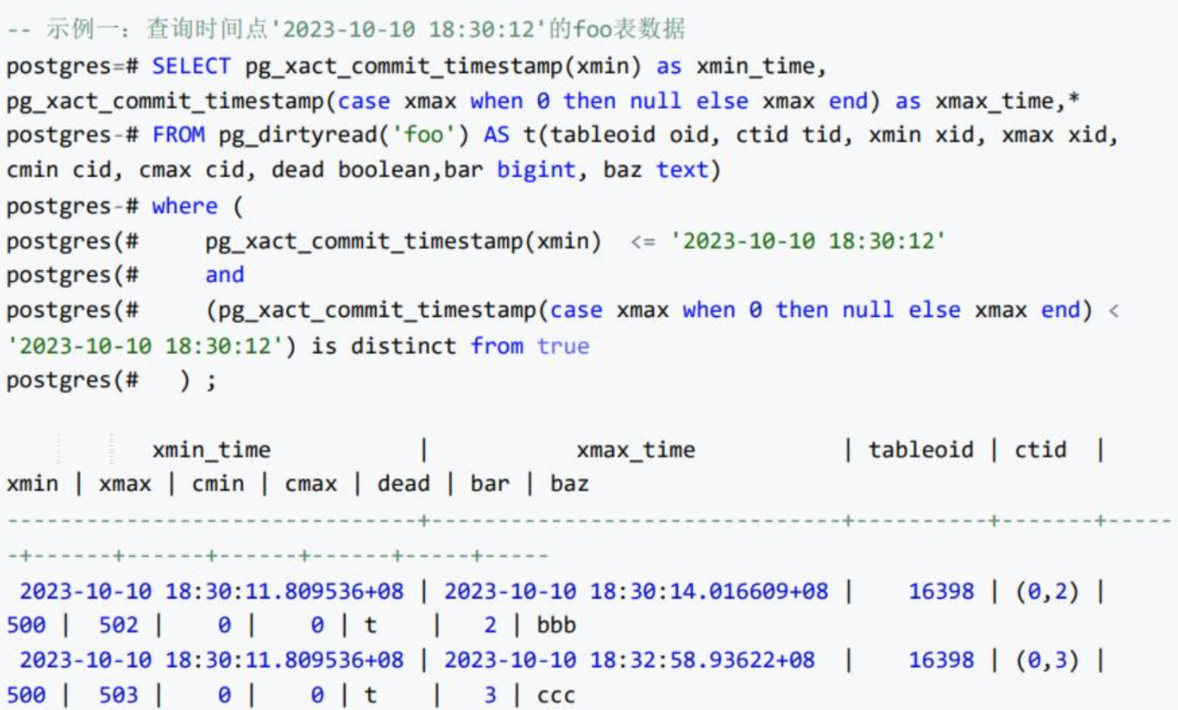
女上司问我:误删除PG百万条数据,可以闪回吗?
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验 擅长主流数据Oracle、MySQL、PG、openGauss运维 备份恢复,安装迁移,性能优化、故障应急处理等可提供技术业务: 1.DB故障处理/疑难杂症远程支援 2.Mysql/PG/Oracl…...
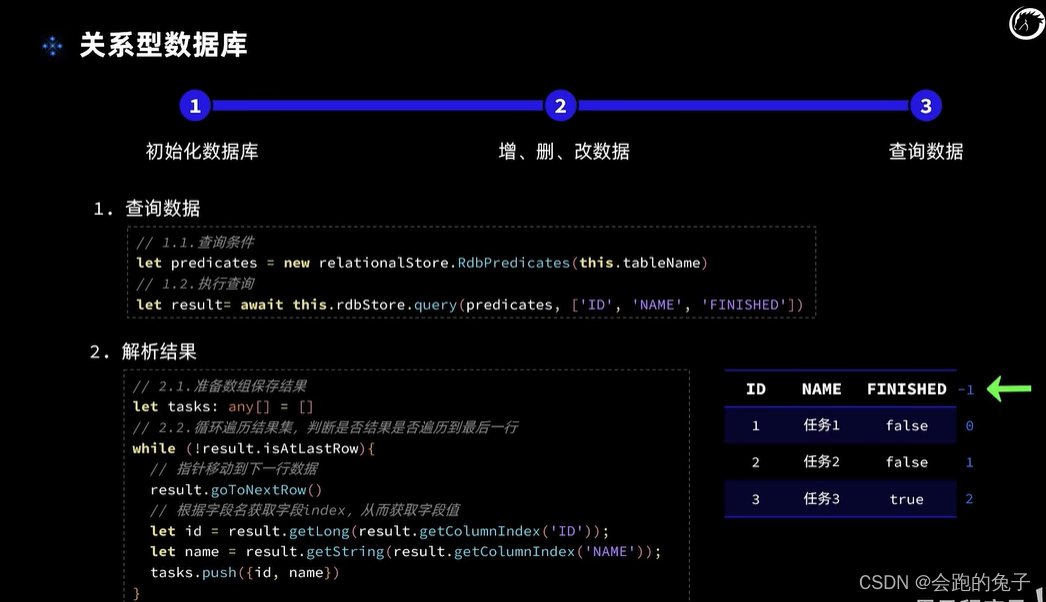
HarmonyOS4-数据持久化
轻量级preferences: 关系型数据库: 增删改: 查询语句: 具体详情代码可参与源码: 黑马大佬写的。 harmonyos-lessons: 黑马程序员B站HarmonyOS课程的基础篇代码部分...

深度学习的社交网络:用户行为分析
1.背景介绍 社交网络是当今互联网的一个重要领域,它们为人们提供了一种快速、便捷的方式来与他人交流、分享信息和建立社交关系。社交网络的数据量巨大,包括用户的个人信息、互动记录、内容等。这些数据为企业和组织提供了丰富的信息来源,可以用于用户行为分析、推荐系统、…...
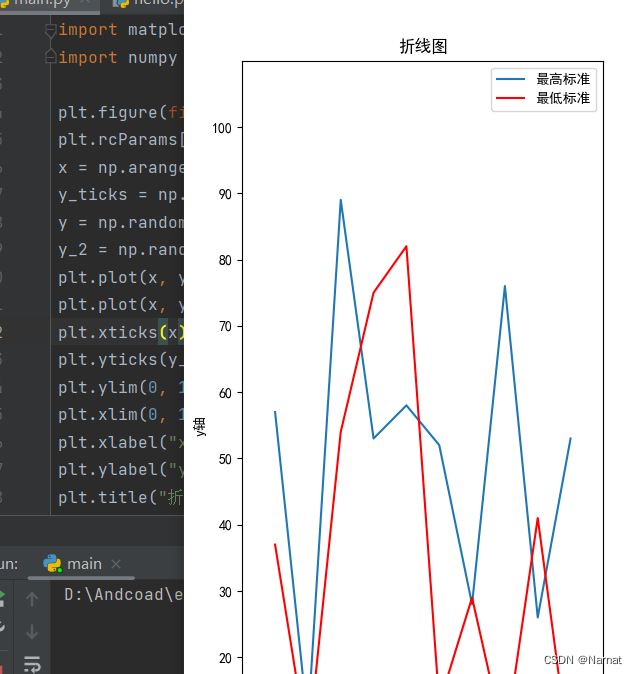
Python 使用 pip 安装 matplotlib 模块(精华版)
pip 安装 matplotlib 模块 1.使用pip安装matplotlib(五步实现):2.使用下载的matplotlib画图: 1.使用pip安装matplotlib(五步实现): 长话短说:本人下载 matplotlib 花了大概三个半小时屡屡碰壁,险些暴走。为了不让新来的小伙伴走我的弯路,特意…...
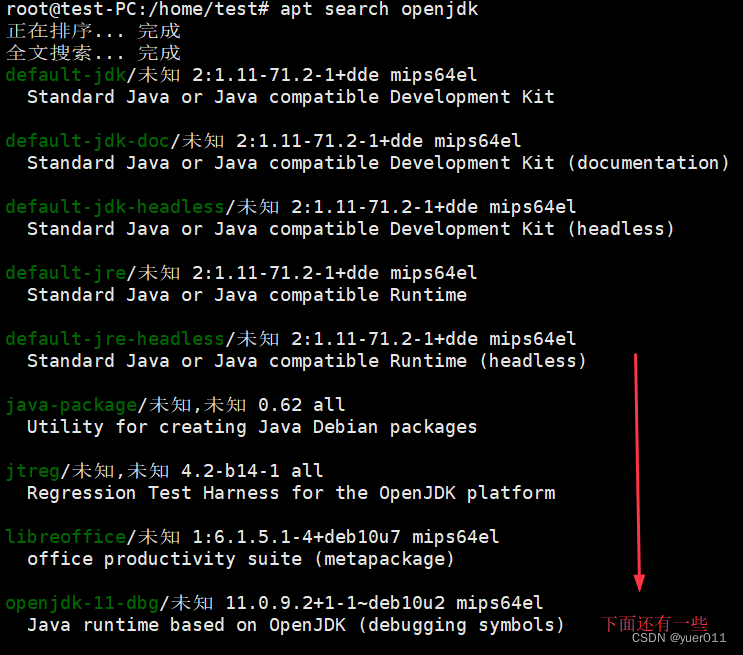
UOS系统-mips架构---Java环境安装
平时都是在windows系统上安装的java环境,今天需要在uos系统安装java1.8的环境,记录一下安装过程。 (以下均在root权限下运行) 一、查找java1.8 jdk版本 apt search openjdkopenjdk-8-jdk/未知,未知 1.8.0.212-2deepin mips64el O…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
