课题学习(二十一)----姿态更新的四元数算法推导
声明:本人水平有限,博客可能存在部分错误的地方,请广大读者谅解并向本人反馈错误。
最近需要使用AEKF对姿态进行结算,所以又对四元数进了深入的学习,本篇博客仅对四元数进行推导,后续会对基于四元数的AEKF算法进行实现。
一、 坐标变化
1.1 基本概念
首先,我对参考坐标系进行了定义,即选择“东-北-天”(或者叫做“右-前-上”),如下图:

并且记:
- p(pitch):俯仰角(绕X轴旋转);
- r(roll):横滚角(绕Y轴旋转);
- y(yaw):航向角(绕Z轴旋转);
并且设角度逆时针旋转为正。
1.2 绕X轴旋转

由上图可以得出由X-Y-Z–>X’-Y’-Z’的变换矩阵:
[ 1 0 0 0 c o s p s i n p 0 − s i n p c o s p ] \begin{bmatrix} 1&0&0 \\ 0&cosp&sinp\\0&-sinp&cosp \end{bmatrix} 1000cosp−sinp0sinpcosp
1.3 绕Y轴旋转

变换矩阵:
[ c o s r 0 − s i n r 0 1 0 s i n r 0 c o s r ] \begin{bmatrix} cosr&0&-sinr \\ 0&1&0\\sinr&0&cosr \end{bmatrix} cosr0sinr010−sinr0cosr
1.4 绕Z轴旋转

变换矩阵:
[ c o s y s i n y 0 − s i n y c o s y 0 0 0 1 ] \begin{bmatrix} cosy&siny&0\\ -siny&cosy&0\\0&0&1 \end{bmatrix} cosy−siny0sinycosy0001
1.5 坐标变换矩阵
在此假设旋转的顺序为:Z–>X–>Y,那么最后的坐标变换矩阵为(注意:一定要把矩阵相乘的顺序搞对):
C n b = C 2 b ( 绕 Y 轴旋转矩阵 ) ∗ C 1 2 ( 绕 X 轴旋转矩阵 ) ∗ C n 1 ( 绕 Z 轴旋转矩阵 ) C_n^b=C_2^b(绕Y轴旋转矩阵)*C_1^2(绕X轴旋转矩阵)*C_n^1(绕Z轴旋转矩阵) Cnb=C2b(绕Y轴旋转矩阵)∗C12(绕X轴旋转矩阵)∗Cn1(绕Z轴旋转矩阵)
= [ c o s r 0 − s i n r 0 1 0 s i n r 0 c o s r ] ∗ [ 1 0 0 0 c o s p s i n p 0 − s i n p c o s p ] ∗ [ c o s y s i n y 0 − s i n y c o s y 0 0 0 1 ] =\begin{bmatrix} cosr&0&-sinr \\ 0&1&0\\sinr&0&cosr \end{bmatrix}*\begin{bmatrix} 1&0&0 \\ 0&cosp&sinp\\0&-sinp&cosp \end{bmatrix}*\begin{bmatrix} cosy&siny&0\\ -siny&cosy&0\\0&0&1 \end{bmatrix} = cosr0sinr010−sinr0cosr ∗ 1000cosp−sinp0sinpcosp ∗ cosy−siny0sinycosy0001
= [ c o s r ∗ c o s y − s i n p ∗ s i n r ∗ s i n y c o s y ∗ s i n y + s i n p ∗ s i n r ∗ c o s y − c o s p ∗ s i n r − c o s p ∗ s i n y c o s p ∗ c o s y s i n p s i n r ∗ c o s y + s i n p ∗ c o s r ∗ s i n y s i n y ∗ s i n r − s i n p ∗ c o s r ∗ c o s y c o s r c o s p ] =\begin{bmatrix} cosr*cosy-sinp*sinr*siny&cosy*siny+sinp*sinr*cosy&-cosp*sinr \\ -cosp*siny&cosp*cosy&sinp\\ sinr*cosy+sinp*cosr*siny&siny*sinr-sinp*cosr*cosy&cosrcosp \end{bmatrix} = cosr∗cosy−sinp∗sinr∗siny−cosp∗sinysinr∗cosy+sinp∗cosr∗sinycosy∗siny+sinp∗sinr∗cosycosp∗cosysiny∗sinr−sinp∗cosr∗cosy−cosp∗sinrsinpcosrcosp
注意: C n b C_n^b Cnb是n系到b系的坐标变换矩阵,而在求解时,是将b系的姿态变换到n系上求解,所以最后要对 C n b C_n^b Cnb转置变为 C b n C_b^n Cbn 。
C b n = ( C n b ) T C_b^n = (C_n^b)^T Cbn=(Cnb)T
= [ c o s r ∗ c o s y − s i n p ∗ s i n r ∗ s i n y − c o s p ∗ s i n y s i n r ∗ c o s y + s i n p ∗ c o s r ∗ s i n y c o s y ∗ s i n y + s i n p ∗ s i n r ∗ c o s y c o s p ∗ c o s y s i n y ∗ s i n r − s i n p ∗ c o s r ∗ c o s y − c o s p ∗ s i n r s i n p c o s r ∗ c o s p ] =\begin{bmatrix} cosr*cosy-sinp*sinr*siny&-cosp*siny&sinr*cosy+sinp*cosr*siny \\ cosy*siny+sinp*sinr*cosy&cosp*cosy&siny*sinr-sinp*cosr*cosy\\ -cosp*sinr&sinp&cosr*cosp \end{bmatrix} = cosr∗cosy−sinp∗sinr∗sinycosy∗siny+sinp∗sinr∗cosy−cosp∗sinr−cosp∗sinycosp∗cosysinpsinr∗cosy+sinp∗cosr∗sinysiny∗sinr−sinp∗cosr∗cosycosr∗cosp
= [ T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 ] =\begin{bmatrix} T_{11}&T_{12}&T_{13}\\ T_{21}&T_{22}&T_{23}\\ T_{31}&T_{32}&T_{33} \end{bmatrix} = T11T21T31T12T22T32T13T23T33
二、 四元数
2.1 基础概念回忆
在课题学习(十七)----姿态更新的四元数算法总结博客中,已经对四元数进行了比较详细的讲解,在这里只对四元数的物理意义重述一次:

其中, u → R = [ l , m , n ] \overrightarrow{u}^R=[l,m,n] uR=[l,m,n],且四元数定义为:
{ q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ
2.2 绕X轴旋转

把 u → R = [ l , m , n ] = [ 1 , 0 , 0 ] \overrightarrow{u}^R=[l,m,n]=[1,0,0] uR=[l,m,n]=[1,0,0]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕X轴的四元数 q x = [ c o s p 2 , s i n p 2 , 0 , 0 ] q_x=[cos\frac{p}{2},sin\frac{p}{2},0,0] qx=[cos2p,sin2p,0,0]
2.3 绕Y、Z轴旋转

绕Y轴旋转:把 u → R = [ l , m , n ] = [ 0 , 1 , 0 ] \overrightarrow{u}^R=[l,m,n]=[0,1,0] uR=[l,m,n]=[0,1,0]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕Y轴的四元数 q y = [ c o s r 2 , 0 , s i n r 2 , 0 ] q_y=[cos\frac{r}{2},0,sin\frac{r}{2},0] qy=[cos2r,0,sin2r,0]
绕Y轴旋转:把 u → R = [ l , m , n ] = [ 0 , 0 , 1 ] \overrightarrow{u}^R=[l,m,n]=[0,0,1] uR=[l,m,n]=[0,0,1]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕Z轴的四元数 q z = [ c o s y 2 , 0 , 0 , s i n y 2 ] q_z=[cos\frac{y}{2},0,0,sin\frac{y}{2}] qz=[cos2y,0,0,sin2y]
2.4 用四元数表示旋转矩阵(坐标变换矩阵)
在第一节中,我们规定了旋转顺序为:Z–>X–>Y,那么最后四元数的旋转矩阵为(参考博客:《欧拉角和四元数之间转换公式推导》): q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy
" ⨂ \bigotimes ⨂"运算在《课题学习(十七)----姿态更新的四元数算法总结 》博客中也有介绍,大家可以参考:

在这部分,我有一点未搞清楚,就是四元数的乘法不满足交换律,即“ P ⨂ Q ≠ Q ⨂ P \bold P \bigotimes \bold Q \neq \bold Q \bigotimes \bold P P⨂Q=Q⨂P” ,那么公式 q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy不能更换相乘的顺序,所以…我搞不懂这个顺序是否正确。
反正最后按照 q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy得到的四元数为:

三、四元数与坐标变换矩阵的关系
在秦永元老师的《惯性导航(第二版)》9.2.2节(P248-P253)中对四元数与坐标变换矩阵的关系进行了推导,大家可以参考学习。
最后得到的四元数表示的坐标变换矩阵为:
C b n = [ q 0 2 + q 1 2 − q 2 2 − q 3 2 2 ( q 1 q 2 − q 3 q 0 ) 2 ( q 1 q 3 + q 2 q 0 ) 2 ( q 1 q 2 + q 3 q 0 ) q 0 2 − q 1 2 + q 2 2 − q 3 2 2 ( q 2 q 3 − q 1 q 0 ) 2 ( q 1 q 3 − q 2 q 0 ) 2 ( q 2 q 3 + q 1 q 0 ) q 0 2 − q 1 2 − q 2 2 + q 3 2 ] C_b^n=\begin{bmatrix} q^2_{0}+q^2_{1}-q^2_{2}-q^2_{3} &2(q_{1}q_{2}-q_{3}q_{0})&2(q_{1}q_{3}+q_{2}q_{0})\\ 2(q_{1}q_{2}+q_{3}q_{0}) &q^2_{0}-q^2_{1}+q^2_{2}-q^2_{3}&2(q_{2}q_{3}-q_{1}q_{0})\\ 2(q_{1}q_{3}-q_{2}q_{0})&2(q_{2}q_{3}+q_{1}q_{0})&q^2_{0}-q^2_{1}-q^2_{2}+q^2_{3} \end{bmatrix} Cbn= q02+q12−q22−q322(q1q2+q3q0)2(q1q3−q2q0)2(q1q2−q3q0)q02−q12+q22−q322(q2q3+q1q0)2(q1q3+q2q0)2(q2q3−q1q0)q02−q12−q22+q32
同时,大家可以对本博客2.4节推导出来的四元数进行反推,比如我计算了 2 ( q 2 q 3 + q 1 q 0 ) 2(q_{2}q_{3}+q_{1}q_{0}) 2(q2q3+q1q0),最后得到的结果就是 s i n p sinp sinp:

四、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602
课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文
课题学习(十六)----阅读《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes Based…》论文
课题学习(十七)----姿态更新的四元数算法总结
课题学习(十八)----捷联测试电路设计与代码实现(基于MPU6050和QMC5883L)
课题学习(十九)----Allan方差:陀螺仪噪声分析
课题学习(二十)----阅读《近钻头井斜动态测量重力加速度信号提取方法研究》论文
相关文章:

课题学习(二十一)----姿态更新的四元数算法推导
声明:本人水平有限,博客可能存在部分错误的地方,请广大读者谅解并向本人反馈错误。 最近需要使用AEKF对姿态进行结算,所以又对四元数进了深入的学习,本篇博客仅对四元数进行推导,后续会对基于四元数的…...

NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL、SQL-PaLM)、新一代数据集BIRD-SQL解读
NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL)、新一代数据集BIRD-SQL解读 NL2SQL基础系列(1):业界顶尖排行榜、权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2…...

双指针运用:删除重复元素、移除元素
26.删除重复元素 题目描述 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元…...

什么是三高架构
三高架构是指在软件系统设计与开发中,注重解决高并发性、高可用性和高性能的架构设计模式。 高并发性:指系统能够处理大量并发请求的能力。在高并发场景下,系统需要具备有效的并发处理机制,以保证系统能够快速、准确地响应大量并…...

Unity 对APK签名
关键代码 PS D:\UnityProject\YueJie> jarsigner -verbose -keystore D:\UnityProject\YueJie\user.keystore -signedjar D:\UnityProject\YueJie\meizuemptyapk-release-signed.apk D:\UnityProject\YueJie\MeizuEmpty-release-unsigned.apk 1 示例 # jarsigner的命令格…...

合成孔径雷达干涉测量InSAR数据处理、地形三维重建、形变信息提取、监测等应用
合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar, InSAR)技术作为一种新兴的主动式微波遥感技术,凭借其可以穿过大气层,全天时、全天候获取监测目标的形变信息等特性,已在地表形变监测、DEM生成、滑坡…...
)
QT进阶------------------QPushButton(快速添加按钮与使用)
1、解决如何快速的添加按钮 在qt中,通常我们喜欢一个按钮添加一个信号与槽,但是这样写太过浪费时间。要是多个按钮那不是要写30个信号与槽,说实话,我不太喜欢这样。 在ui中,只要拖动按钮,会自动生成按钮的名…...
Vue项目管理器创建项目
黑马程序员JavaWeb开发教程 文章目录 1、创建新项目2、详情3、预设4、功能5、配置6、是否保存为预设模板7、正在创建项目8、创建完成 1、创建新项目 2、详情 3、预设 选择手动,点击下一步 4、功能 只需要额外选择一项–Router 即可,其余的保持默认&a…...
PHP-extract变量覆盖
[题目信息]: 题目名称题目难度PHP-extract变量覆盖1 [题目考点]: 变量覆盖指的是用我们自定义的参数值替换程序原有的变量值,一般变量覆盖漏洞需要结合程序的其它功能来实现完整的攻击。 经常导致变量覆盖漏洞场景有:$$&#x…...

研究表明,全球互联网流量竟有一半来自机器人
据Cyber News消息,Thales Imperva Bad Bot近期做了一份报告,显示在2023年有49.6%的互联网流量竟来自机器人,比上一年增长 2%,达到自2013年以来观察到的最高水平。 报告称,这一趋势正对企业组织产生负面影响,…...

橡胶衬板的更换与安装
橡胶衬板的更换与安装 橡胶衬板作为一种重要的工业材料,广泛应用于各种设备和机器中,以提供减震、防滑、耐磨等功能。然而,随着时间的推移和使用频率的增加,橡胶衬板可能会磨损或老化,需要及时更换和安装。本文将介绍…...

Compose 简单组件
文章目录 Compose 简单组件TextText属性使用AnnotatedStringSpanStyleParagraphStyle SelectionContainer 和 DisableSelectionClickableText TextFieldTextField属性使用OutlinedTextFieldBasicTextFieldKeyboardOptions 键盘属性KeyboardActions IME动作 ButtonButton属性使用…...

第十一届蓝桥杯省赛真题(C/C++大学B组)
目录 试题A :门牌制作 试题B :既约分数 试题C :蛇形填数 试题D :跑步训练 试题E :七段码 试题F :成绩统计 试题G :回文日期 试题H :字串分值 试题I :平面切分&a…...
Qt 实战(2)搭建开发环境 | 2.1、Windows下安装QT
一、Windows下安装QT 1、QT官网 QT官网:https://download.qt.io/,打开官网地址,如下: 目录结构介绍 目录说明snapshots预览版,最新的开发测试中的 Qt 库和开发工具onlineQt 在线安装源official_releases正式发布版&am…...
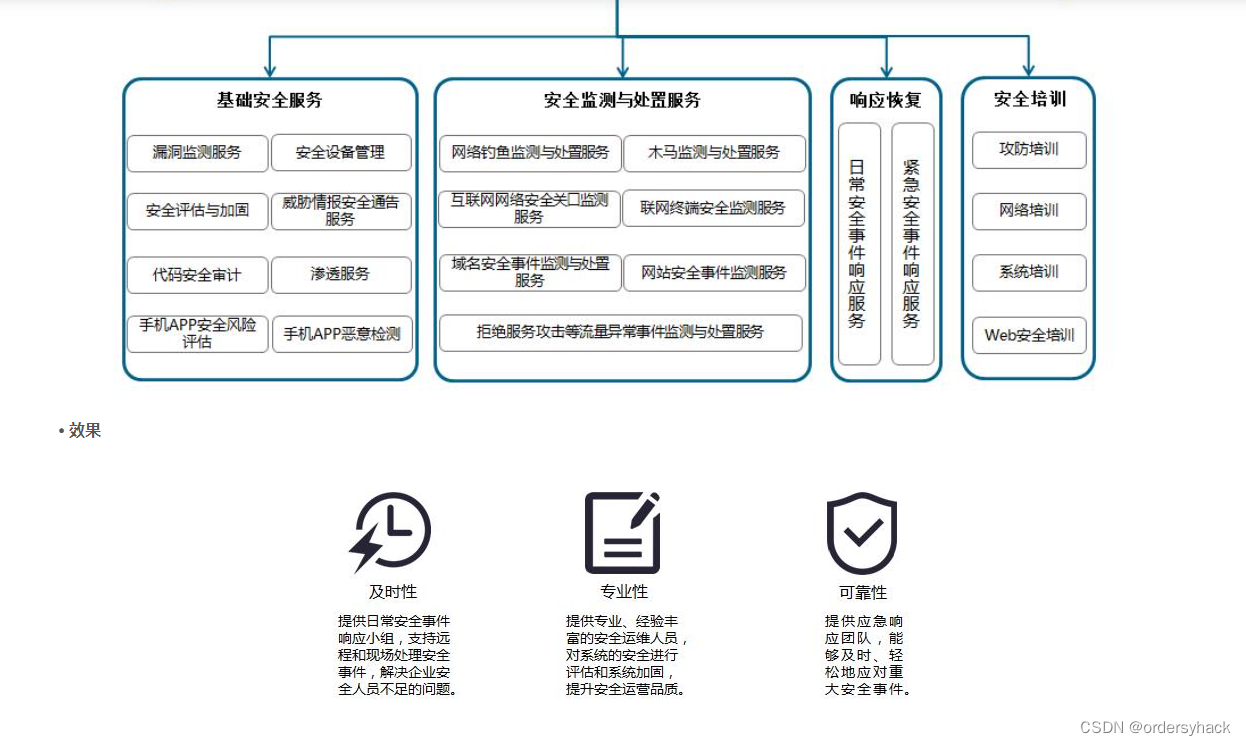
校园通用型发生网络安全事件解决方案
已知校园多教学楼、多教学机房、非标网络机房缺乏防护设备、检测设备、安全保护软件(杀软) 切断所有外网,断网理!!!!!!!!!!!…...

数通HCIE考试分享:考前心态很重要,心情放松好过一次练习
誉天数通HCIE晚班火热预约中!真机实验考前辅导备考资料,名师保驾护航,助你稳定通关!识别二维码,即可获取免费试听名额! 备考阶段 我是去年10月底完成了笔试考试,在笔试之前就将PY的课程过了一遍…...
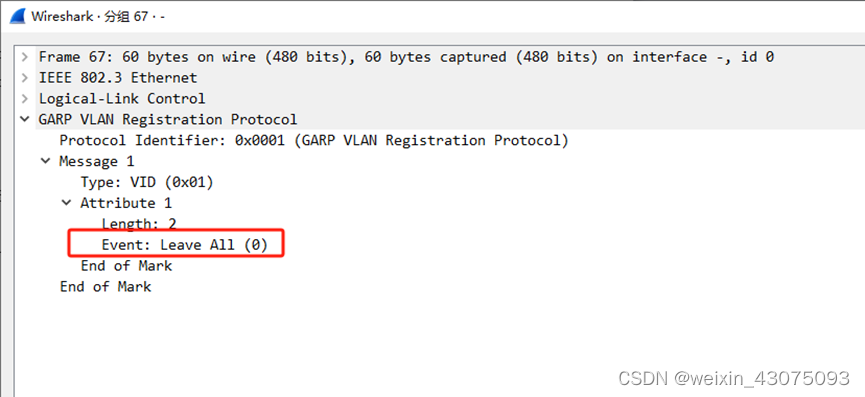
GVRP协议与动态、静态vlan
一、GVRP协议使用场景 1、当实际组网复杂到网络管理员无法短时间内了解网络的拓扑结构,或者是整个网络的VLAN太多时,工作量会非常大,而且非常容易配置错误。在这种情况下,用户可以通过GVRP的VLAN自动注册功能完成VLAN的配置。 2、…...

shell脚本启动jar包
1、启动脚本的命令start.sh # 设置jar包名称 JAR_NAME"ruoyi-admin.jar" # 使用pgrep查找jar包名称的进程,如果存在,返回0(表示找到了进程) if pgrep -f "$JAR_NAME" >/dev/null thenecho "Jar进程已…...

qt 元对象系统及属性系统
Qt元对象系统(QMetaObject) Qt 的元对象系统叫 Meta-Object-System,提供了对象之间通信的信号与槽机制、运行时类型信息和动态属性系统。即使编译器不支持RTTI(RTTI的实现耗费了很大的时间和存储空间,这就会降低程序的性能)&…...

2024年MathorCup数学建模A题移动通信网络中PCI规划问题解题文档与程序
2024年第十四届MathorCup高校数学建模挑战赛 A题 移动通信网络中PCI规划问题 原题再现: 物理小区识别码(PCI)规划是移动通信网络中下行链路层上,对各覆盖小区编号进行合理配置,以避免 PCI 冲突、PCI 混淆以及 PCI 模3 千扰等现象。PCI 规划…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
