浅谈C语言中异或运算符的10种妙用
目录
1、前言
2、基本准则定律
3、妙用归纳
4、总结
1、前言
C语言中异或运算符^作为一个基本的逻辑运算符,相信大家都知道其概念:通过对两个相同长度的二进制数进行逐位比较,若对应位的值不同,结果为 1, 否则结果为 0。
但是它在实际使用中到底会有哪些应用场景或者说是有在一些编程技巧中该如何使用,本文总结归纳了一些异或运算符的编程时实用方法思路以供参考,如有其它好用的功能,也可提出一起分享。
2、基本准则定律
首先需要明确的是异或运算的几个基本准则定律,这些准则定律为异或运算的巧妙应用提供了基础。
-
交换律:对于任意变量 a 和 b,a ^ b 等于 b ^ a。
-
结合律:对于任意变量 a、b 和 c,(a ^ b) ^ c 等于 a ^ (b ^ c)。
-
自反性:任何数与自身进行异或操作结果为0,即 a ^ a = 0。
-
零元素性质:任何数与0进行异或操作结果为自身,即 a ^ 0 = a。
-
分配律:a ^ (b & c) = (a ^ b) & (a ^ c),其中 & 表示按位与操作。
-
奇偶性:一个数字和1做异或运算,可以判断它的奇偶性。如果结果为0,表示这个数字是偶数,如果结果为1,表示这个数字是奇数。
3、妙用归纳
暂归纳了10种在编程中经常遇见的异或运算使用的方法。
(1)两个值的快速比较
例如比较两个值是否相等时,一般我们使用这个 a==b,如果两个数相等 ,a ^ b 的结果为零。
if(a^b == 0) {//a和b若相同则为true
}(2)数据交换
利用异或运算的性质可以进行两个数的交换,不会利用额外的变量。
void swap()
{ a=a^b;b=b^a;a=b^a;
}注意利用异或运算进行数据交换有个前提:要交换的两个数必须在在不同的内存,不然会出现问题。如果 a 和 b 是同一个地址呢?比如,我们调用的是 swap(a[i], a[j]),当 i == j时,利用异或运算进行数据交换是错误的。
在这种情况下,我们第一步做的 a ^= b,实际上就是 a[i] ^= a[i]。这将直接让a[i]中的元素等于0,而丢失原本存在a[i]中的元素。后续这个元素就再也找不回来了。针对这个问题解决方案是在做这个交换之前,判断一下 a 和 b的地址是否相同。也可以把逻辑改变为,判断一下a和b是否相同。如果相同,则什么都不做。
(3)加减法
如二进制加法01 + 01 = 10,而异或运算是01 ^ 01 = 00,它其实做了加法,但高位不进位,所以异或又称不进位加法。
如二进制减法10 - 01 = 01,而异或运算是10 ^ 01 = 11,也可以看做个位0向高位借了一个1当2来用,但高位不减1,所以异或也可以称为不退位减法。
利用异或的这个特性,只要再解决一下进位和退位问题,就可以实现加减法了。这也是为什么CPU里面都是做位运算的逻辑门电路,却能实现数值计算。
int plus(int a, int b) {int sum, addition;while (b != 0) {// 加法(未考虑进位)sum = a ^ b;// 进位值,二进制中1 + 1的场景才会进位,//a & b只有两个都为1,结果才是1,左移一位,就是进位值了addition = (a & b) << 1;// 赋值,下次循环将进位加到a里面来,直到进位等于0a = sum;b = addition;}return a;
}int subtraction(int a, int b){int sum, abdication;while (b != 0){// 减法(未考虑退位)sum = a ^ b;// 退位值,二进制中0 - 1的场景才会退位,//~a & b只有a=0,b=1,结果才是1,左移一位,就是退位值了abdication = (~a & b) << 1;// 赋值,下次循环将退位再从a中减掉,直到退位等于0a = sum;b = abdication;}return a;
}(4)数据备份
使用异或也可以很容易实现多个数据的互相备份,假如有数据a、b、c,则d = a ^ b ^ c,然后把数据d备份下来。
当a丢失时,可使用d ^ b ^ c来恢复
当b丢失时,可使用d ^ a ^ c来恢复
当c丢失时,可使用d ^ a ^ b来恢复由此可见备份了一份数据d后,丢失了其他任何一个数据,都可以通过备份数据与其它数据异或恢复回来,磁盘阵列技术raid5的数据备份原理,用的就是这个特性。
(5)数据加解密
在例如通信时需要对数据使用简单的加解密方法时,使用异或操作可以进行明文数据的加解密,。比如明文数据是message,密钥是key,加密后的数据是secret,确保通信发送方和通信接收方都存储了相同的key,key可以使用rand()生产一串随机数,则举例说明:
// 加密
secret = message ^ key
0x2C0E = 0x89AB ^ 0xA5A5
// 解密
message = secret ^ key
0x89AB = 0x2C0E ^ 0xA5A5美国数学家香农证明了只要满足以下两个条件,异或加密是无法破解的。
-
key的长度大于等于message。
-
key必须是一次性的,且每次都要随机产生。
理由很简单,如果每次的 key 都是随机的,那么产生的secret具有所有可能的值,而且是均匀分布,无法从secret看出 message 的任何特征。也就是说,它具有最大的"信息熵",因此完全不可能破解。这被称为异或的"完美保密性"。为了让异或加密更可靠,可以添加一些其他操作,例如对数据进行循环位移或取反的操作。
(6)数据奇偶数判断
由于异或运算要先转化为二进制数,而偶数的二进制数的最后一位必定是0,奇数的二进制数的最后一位必定是1。
因此,要判断的数与1异或得到的结果 - 要判断的数==1,说明该数是偶数,反之是奇数!
int a = 12345; //a=123456
if ((a ^ 1) - a == 1) {"是偶数!";
} else {"是奇数!";
}(7)出现奇偶次的找数问题
一个数组中有一种数出现了奇数次,其他数都出现了偶数次,怎么找到这一个数?
分析:利用异或性质a ^ a=0,则出现偶数的数字相异或为0,而出现奇数次的异或结果为本身,那么,将所有的数异或后,就是要找的这个出现奇数次的数。
int ReOddNum1(int arr[], int len)
{int re = arr[0];for (int i=1;i<len;i++){re = arr[i] ^ re;}return re;
}一个数组中有两种数出现了奇数次,其他数都出现了偶数次,怎么找到这两个数?
step1:将所有数异或,得到re=a^b;
step2:提取re最右侧的“1”(取反,+1,自身相与);
step3:将所有该位为“1”的数相异或,得到的数便为a或者b;
step4:再次相与两个结果,得到另一个数。
int* ReOddNum2(int arr[], int len)
{int re = arr[0];int rr[2] = { 0,0 };//第一步:将所有数异或,得到a^bfor (int i = 1; i < len; i++){re = arr[i] ^ re;}//第二步:提取re最右侧的“1”(取反,+1,自身相与)int rightone = re&(~re + 1);//第三步:将所有该位为“1”的数相异或,得到的数便为a或者bint re1 = 0;for (int i = 0; i < len; i++){if ((arr[i]&rightone)!=0){re1 = arr[i] ^ re1;} }rr[0] = re1;//第四步:再次相与两个结果,得到另一个数rr[1] = re1^re;return rr;
}(8)奇偶校验
首先先看一个例子理解下:判断一个二进制数中1的数量是奇数还是偶数。
求10110101中出现1的数量是奇数还是偶数;可将10110101逐位异或操作,结果为1就是奇数个1,结果为0就是偶数个1。
奇校验:原始码+1位校验位,总共有奇数个1;
偶校验:原始码+1位校验位,总共有偶数个1。
比如为原始码添加奇偶校验位:
原始码:1101010
判断1的个数是否为偶数:1^1^0^1^0^1^0=0,因为逐位异或的结果为0,所以1的个数为偶数,奇校验则在原数据末尾添1,变成11010101;偶校验则在原数据末尾添0,变成11010100。
(9)对某些特定的位翻转
由于不管是0或者1与1做异或操作后将得到原值的相反值,因此当我们需要翻转一个整数的某些位时,我们可以使用位异或运算来实现掩码操作,将对应的数据位进行翻转。
//定义一个整数n
int a = 0x0f; //二进制表示为00001111
//如果需要翻转a的第4和第5位,则定义掩码mask
int mask = 0x18; //二进制表示为00011000
//使用位异或运算翻转n的第3位和第4位
n = n ^ mask; //结果为二进制表示为00010111在单片机编程中对GPIO输出控制LED的闪烁原理也是如此,定义了一个宏,直接通过GPIOA口对ODR寄存器进行操作,异或PIN2的位。实现引脚PA2输出高低电平的翻转控制LED闪烁。
// PA2引脚输出电平翻转
#define LED_TOGGLE() GPIOA->ODR ^= GPIO_PIN_2(10)数据符号判断
例如判断两个int32类型的数据的符号是否相同,其中31是符号位的偏移量:
if (((a ^ b) >> 31) & 1) {"符号不相同!";
} else {"符号相同!";
}4、总结
总之,异或运算是一种重要的二进制运算,在实际代码编程中有着广泛的应用。需要深刻的去理解异或运算符的几条基本准则定律,就能够快速地完成数字的交换、计算、去重等操作,为我们在功能开发中提供便利。
小tips:归根到底在布尔代数中,其实只需要与、或、非运算就可以实现所有其它运算,所以异或运算实际可以通过与、或、非实现,最直观的表示方式如下:
a ^ b = (~a & b) | (a & ~b) ↓↓↓更多技术内容和书籍资料获取,入群技术交流敬请关注“明解嵌入式”↓↓↓
相关文章:

浅谈C语言中异或运算符的10种妙用
目录 1、前言 2、基本准则定律 3、妙用归纳 4、总结 1、前言 C语言中异或运算符^作为一个基本的逻辑运算符,相信大家都知道其概念:通过对两个相同长度的二进制数进行逐位比较,若对应位的值不同,结果为 1, 否则结果为 0。 但是…...
Canal--->准备MySql主数据库---->安装canal
一、安装主数据库 1.在服务器新建文件夹 mysql/data,新建文件 mysql/conf.d/my.cnf 其中my.cnf 内容如下 [mysqld] log_timestampsSYSTEM default-time-zone8:00 server-id1 log-binmysql-bin binlog-do-db mall # 要监听的库 binlog_formatROW2.启动数据库 do…...
vs配置opencv运行时“发生生成错误,是否继续并运行上次的成功生成”BUG解决办法
vs“发生生成错误,是否继续并运行上次的成功生成” 新手在用vs配置opencv时遇到这个错误时,容易无从下手解决。博主亲身经历很有可能是release/debug模式和配置文件不符的问题。 在配置【链接器】→【输入】→【附加依赖项】环节,编辑查看选择…...

Dryad Girl Fawnia
一个可爱的Dryad Girl Fawnia的三维模型。她有ARKit混合形状,人形装备,多种颜色可供选择。她将是一个完美的角色,幻想或装扮游戏。 🔥 Dryad Girl | Fawnia 一个可爱的Dryad Girl Fawnia的三维模型。她有ARKit混合形状,人形装备,多种颜色可供选择。她将是一个完美的角色…...
)
内存相关知识(新)
基本概念 内存层次结构:内存层次结构是一种层次化的存储设备结构,它包括寄存器、缓存、主存和辅助存储器。每一层次的存储设备都有不同的速度、容量和成本。 内存单元:内存被划分为一系列连续的内存单元,每个单元都有一个唯一的地…...

C++从入门到精通——static成员
static成员 前言一、static成员概念例题 二、 static成员的特性特性例题静态成员函数可以调用非静态成员函数吗非静态成员函数可以调用类的静态成员函数吗 前言 一、static成员 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之…...

【K8S:初始化】:执行kubeadm显示:connection refused.
文章目录 [root10 kubernetes]# kubeadm init --kubernetes-versionv1.23.0 --image-repositoryregistry.aliyuncs.com/google_containers --apiserver-advertise-address192.168.56.104 [init] Using Kubernetes version: v1.23.0 [preflight] Running pre-flight checks [pre…...
msvcp140_1.dll是什么?找不到msvcp140_1.dll丢失解决方法
msvcp140_1.dll 文件是一个与 Microsoft Visual C 2015 Redistributable 相关的动态链接库(DLL),它在 Windows 系统中扮演着重要角色,尤其对于那些依赖于 Visual C 运行时环境的应用程序和游戏来说。以下是关于 msvcp140_1.dll 文…...

【Java探索之旅】掌握数组操作,轻松应对编程挑战
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java编程秘籍 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、数组巩固练习1.1 数组转字符串1.2 数组拷贝1.3 求数组中的平均值1.4 查找数组中指…...
深入理解同步与异步编程及协程管理在Python中的应用
文章目录 1. 同步与异步函数的对比1.1 同步函数1.2 异步函数1.3 对比 2. 管理多个协程与异常处理2.1 并发执行多个协程2.2 错误处理2.3 任务取消 本文将探索Python中同步与异步编程的基本概念及其区别。还会详细介绍如何使用asyncio库来有效管理协程,包括任务的创建…...

Win10本地更新无法升级win11 的0x80080005解决方法
Win10本地更新无法升级win11 Visual Studio 2022 运行项目时,本文提供了错误“指定的程序需要较新版本的 Windows”的解决方法。 更新时提示:0x80080005 解决方法 1、下载Windows11InstallationAssistant.exe 【免费】Windows11InstallationAssista…...
互联网轻量级框架整合之MyBatis核心组件
在看本篇内容之前,最好先理解一下Hibernate和MyBatis的本质区别,这篇Hibernate和MyBatis使用对比实例做了实际的代码级对比,而MyBatis作为更适合互联网产品的持久层首选必定有必然的原因 MyBatis核心组件 MyBatis能够成为数据持久层首选框&a…...
springboot websocket 持续打印 pod 日志
springboot 整合 websocket 和 连接 k8s 集群的方式参考历史 Java 专栏文章 修改前端页面 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>Java后端WebSocket的Tomcat实现</title><script type"text/javasc…...
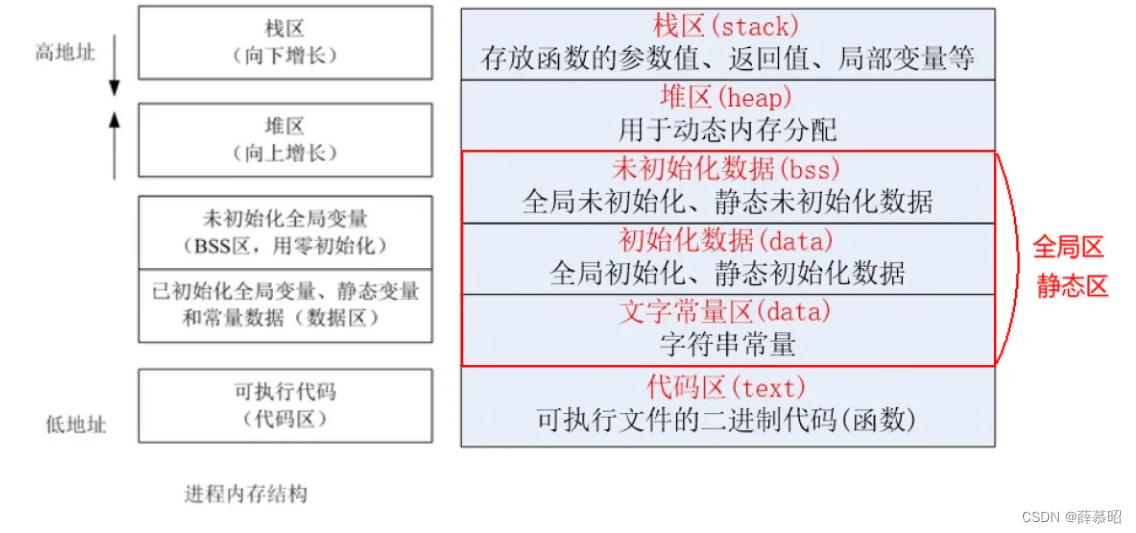
C代码编译过程与进程内存分布
C代码编译过程 在这篇文章中,我们将探讨C语言代码的编译流程以及进程在运行时的内存布局。编译过程通常包括几个关键步骤:预处理、编译、汇编和链接。 预处理阶段主要是处理源代码文件中的宏定义、头文件包含和条件编译指令。在此阶段,编译…...
Windows 部署ChatGLM3大语言模型
一、环境要求 硬件 内存:> 16GB 显存: > 13GB(4080 16GB) 硬盘:60G 软件 python 版本推荐3.10 - 3.11 transformers 库版本推荐为 4.36.2 torch 推荐使用 2.0 及以上的版本,以获得最佳的推理性能 二、部…...

JS相关八股之什么是事件循环
在JavaScript中,“事件循环”(Event Loop)是一个非常重要的概念,它是指JavaScript引擎如何在单线程中处理异步操作的机制。单线程意味着在任意时刻,JavaScript代码只能执行一个任务。 一.事件循环的工作流程大致如下&…...
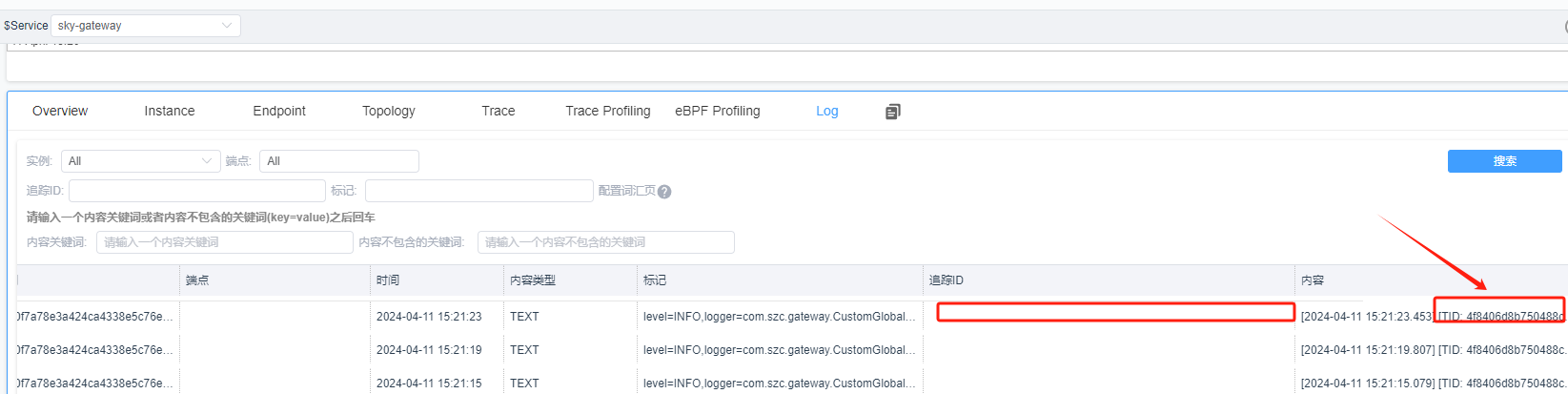
SpringCloud集成Skywalking链路追踪和日志收集
1. 下载Agents https://archive.apache.org/dist/skywalking/java-agent/9.0.0/apache-skywalking-java-agent-9.0.0.tgz 2. 上传到服务器解压 在Spring Cloud项目中,每部署一个服务时,就拷贝一份skywalking的agent文件到该服务器上并解压。不管是部署…...

HTTP 域名和主机是一回事吗?有了主机和域名,如何建站?
域名不等于主机名,例如baidu.com是一个权威域的域名,但是根本没有一个主机的名字叫做baidu.com,但是dns.baidu.com就是一个主机名,它就是负责baidu.com的服务器的主机名,www.baidu.com也是一个主机名,它是百度web服务器的主机名。…...

运营干货:四个技巧掌握爆款选题方法
在运营工作中,选题是一项至关重要的工作,选对了一个热门话题,就能吸引大量用户的关注和互动,从而取得更好的运营成果。 今天,就给大家分享四个爆款选题方法,让大家的运营更上一层楼! 第一种&a…...

柯桥商务口语之怎么样说英语更加礼貌?十个礼貌用语get起来!
当你在国外需要帮助的时候,这些礼貌用语真的是能够帮到你的哦 1.Would/Could you help me? 你可帮助我吗? 相信有些人想请求帮助的时候,一开口就用Can you,这个用在朋友或者熟人上面当然是没有问题的,但是如果是向…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
