2017NOIP普及组真题 4. 跳房子
线上OJ:
一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid=1417\
核心思想
首先、本题中提到 “ 至少 要花多少金币改造机器人,能获得 至少 k分 ”。看到这样的话语,基本可以考虑要使用 二分答案。
那么,本题中的 答案 是什么?就是: 在确定维修金币g的情况下,能获得的分数是否会> k 。
由于本题中的 格子在同一条直线上,且只能从左往右跳,所以 每一种答案 都可以使用 动态规划 来解决。
而且动态规划的 dp 方程也很好找,因为 当前格子的最高分 肯定是由 之前某个最高分的格子跳过来的,即:
d p [ i ] = m a x ( d p [ i ] , d p [ j ] + a [ i ] ) dp[i] = max(dp[i], dp[j] + a[i]) dp[i]=max(dp[i],dp[j]+a[i])
所以,我们从 i 号格子前面的第一个格子开始查找得分最高的格子。在这里需要注意的是:不是所有的 j 都需要查找。只有当 j 的跳跃区间 [d-g, d+g] 能够触达(或包含)i坐标 的时候,这个 j 才能用于更新dp[i]。
以下三个举例(及配图)便于理解j和i的关系
举例1: i 号格子位于坐标10,j 号格子位于坐标5(此时 j 的跳跃区间为 [2,4],也就是 j 能跳到的地方为[7,9]),所以此时 j 号格子无法触达 i,所以 j 号格子不需要用于更新dp[i]。
举例2: i 号格子位于坐标10,j 号格子位于坐标5(此时 j 的跳跃区间为 [2,6],也就是 j 能跳到的地方为[7,11]),所以此时 j 号格子可以触达 i,所以 j 号格子需要用于更新dp[i]。
举例3: i 号格子位于坐标10,j 号格子位于坐标5(此时 j 的跳跃区间为 [6,8],也就是 j 能跳到的地方为[11,13]),所以此时 j 号格子无法触达 i,所以 j 号格子不需要用于更新dp[i]。

综上所述,有效的 j 点应该满足
d − g < = x [ i ] − x [ j ] < = d + g d-g < = x[i] - x[j] < = d+g d−g<=x[i]−x[j]<=d+g,
我们令左边界为 l = d - g,右边界为 r = d + g,则仅当 满足①和②式的 j 点 才参与dp[i]的运算
x [ i ] − x [ j ] > = l x[i] - x[j] > = l x[i]−x[j]>=l; ①
$x[i] - x[j] < =r $; ②
题解代码:
解法一:二分答案 + 动态规划(仅80%分数)
#include <bits/stdc++.h>
#define ll long long
#define MAXN 500005using namespace std;int n, d, k;ll x[MAXN], s[MAXN], dp[MAXN];// 检查花费g个金币进行改造后,最高得分是否会超过 k
bool check(int g)
{// 计算在花费g金币下,机器人每次向右跳的距离边界[l, r] = [d-g, d+g]。注:左边界不能小于1 int l = max(1, d - g); // 机器人每次能跳跃的最小距离 int r = d + g; // 机器人每次能跳跃的最大距离memset(dp, 0xaf, sizeof(dp)); // 全部初始化为一个很小的数。dp[0] = 0; // 数据即分数都从第一个格子开始,所以第0个格子初始化为0分 for(int i = 1; i <= n; i ++){// 从i的前一个格子开始枚举j,直到j枚举到起点(如果i和j之间的距离已经超过弹跳上限r,则没必要继续j--了) for(int j = i - 1; (j >= 0) && (x[i] - x[j] <= r); j --){// 如果j号格子距离i号格子不能太近,至少要≥机器人弹跳的最小距离”,否则就j--,寻找更远的j if(x[i] - x[j] >= l){// i的最高得分应该是从前面能跳过来的格子j里得分最高的格子跳过来的dp[i] = max(dp[i], dp[j] + s[i]); if(dp[i] >= k) return true;} }}return false;
}int main()
{scanf("%d%d%d", &n, &d, &k);for(int i = 1; i <= n; i ++)scanf("%lld%lld", &x[i], &s[i]);// 由于x[i]的坐标范围可到 10^9,在极端情况下有可能前面全是负值,只有最后一个x[n]是正值,此时要搜索的答案g也会达到 10^9(即一步跳到最后一个正值)。所以二分答案时 r 应取到 x[n]。但如此一来,效率就变低了,只能拿到80%的分数int l = 0, r = x[n], mid, ans = -1; while(l <= r){mid = (l + r) >> 1;if(check(mid)){ans = mid;r = mid - 1;}else l = mid + 1;}cout << ans << endl;return 0;
}以上方法只能拿到80分,因为二分答案的右区间 r 取值为 x[n],数据过于庞大。
解法二、二分答案 + 动态规划 + 单调队列(100%)
由于 二分答案时的 r 取值为 x[n]过于庞大,所以此时考虑对 check 函数进行优化。由于 dp[i] 是之前的某个最大值 dp[j] 跳过来,所以可以考虑优先队列;同时由于 j 是有区间的,所以考虑优先队列的升级版–单调队列(单调队列适合在一个动态小区间中寻找极值)
#include <bits/stdc++.h>
#define ll long long
#define MAXN 500005using namespace std;int n, d, k;ll x[MAXN], s[MAXN], dp[MAXN];//检查花费g个金币进行改造后,最高得分是否会超过k
bool check(int g)
{// 计算在花费g金币下,机器人每次向右跳的距离边界[l, r] = [d-g, d+g]。注:左边界不能小于1 ll l = max(1, d - g); // 机器人每次向右跳的最小距离 ll r = d + g; // 机器人每次向右跳的最大距离memset(dp, 0xaf, sizeof(dp));dp[0] = 0; // 数据即分数都从第一个格子开始,所以第0个格子初始化为0分 ll j = 0;deque<int> q;for(int i = 1;i <= n;i ++){// 根据区间[l, r],剔除队尾的 while(x[i] - x[j] >= l) // 根据i查找所有符合跳跃左边界的j {// 将队列中比 dp[j] 还小的直接移除 (由于按照单调队列存储,故从队尾判断)while( !q.empty() && dp[q.back()] < dp[j] )q.pop_back();q.push_back(j); // 把 j 放到单调队列的尾部,此时dp[j]是当前区间内最小的 j ++;}// 根据区间 [l, r],剔除队头的 while(!q.empty() && x[q.front()] + r < x[i]) // 如果最大的格子距离i太远,已经超过弹跳上限r q.pop_front(); // 则说对对头元素不在 [l,r] 内,弹出 if(!q.empty()) // 如果此时队列依然非空,则取队首的元素下标 q.front() 来做 dp dp[i] = dp[q.front()] + s[i];if(dp[i] >= k)return true;}return false;
}int main()
{scanf("%d%d%d", &n, &d, &k);for(int i = 1; i <= n; i ++)scanf("%lld%lld", &x[i], &s[i]);int l = 0, r = x[n], mid, ans = -1;while(l <= r){mid = (l + r) >> 1;if(check(mid)){ans = mid;r = mid - 1;}else l = mid + 1;}cout << ans << endl;return 0;
}
备注:这道题想 混分 有点 难,虽然参考输入样例2中给出了输出 -1 的场景(即:所有正的分数总和依然达不到目标分数k),但是实际的测试数据中并没有这种情况,所以这道题骗分骗不到。
相关文章:

2017NOIP普及组真题 4. 跳房子
线上OJ: 一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid1417\ 核心思想 首先、本题中提到 “ 至少 要花多少金币改造机器人,能获得 至少 k分 ”。看到这样的话语,基本可以考虑要使用 二分答案。 那么,本题中…...

网络与 Internet因特网的基本概念
目录 网络Internet (互联网或互连网)Internet(因特网)待续、更新中 网络 指将分布在不同地理位置的、相同或不同类型的网络通过网络互连设备(中继器、网桥、路由器或网关等)相互连接,形成一个范…...

vue-router 中 router-link 与 a 标签的区别
文章目录 前言 a标签定义 router-link定义 总结 前言 vue-router 中 router-link 与 a 标签的区别 a标签定义 <a> 标签定义超链接,用于从一张页面链接到另一张页面。 从一张页面跳转到另一张页面,但从这里来说就违背了多视图的单页Web应用这个…...
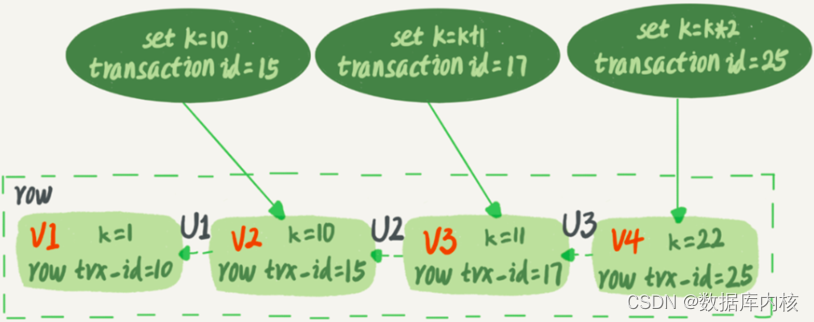
MySQL基础知识——MySQL事务
事务背景 什么是事务? 一组由一个或多个数据库操作组成的操作组,能够原子的执行,且事务间相互独立; 简单来说,事务就是要保证一组数据库操作,要么全部成功,要么全部失败。 注:MyS…...

【架构方法论(一)】架构的定义与架构要解决的问题
文章目录 一. 架构定义与架构的作用1. 系统与子系统2. 模块与组件3. 框架与架构4. 重新定义架构:4R 架构 二、架构设计的真正目的-别掉入架构设计的误区1. 是为了解决软件复杂度2. 简单的复杂度分析案例 三. 案例思考 本文关键字 架构定义 架构与系统的关系从业务逻…...
基于springboot实现人口老龄化社区服务与管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现人口老龄化社区服务与管理系统演示 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了人口老龄化社区服务与管理平台的开发全过程。通过分析人口老龄化社区服务与管理平台方面的不足ÿ…...
代码随想录算法训练营第三十七天| LeetCode 738.单调递增的数字、总结
一、LeetCode 738.单调递增的数字 题目链接/文章讲解/视频讲解:https://programmercarl.com/0738.%E5%8D%95%E8%B0%83%E9%80%92%E5%A2%9E%E7%9A%84%E6%95%B0%E5%AD%97.html 状态:已解决 1.思路 如何求得小于等于N的最大单调递增的整数?98&am…...

C++动态内存管理 解剖new/delete详细讲解(operator new,operator delete)
讨厌抄我作业和不让我抄作业的人 讨厌插队和不让我插队的人 讨厌用我东西和不让我用东西的人 讨厌借我钱和不借给我钱的人 讨厌开车加塞和不让我加塞的人 讨厌内卷和打扰我内卷的人 一、C中动态内存管理 1.new和delete操作内置类型 2.new和delete操作自定义类型 二、operat…...

python-re正则笔记0.2.0
1. 匹配linux文件路径 from re import match, search,findall str"sh refreshConfig.sh /opt/client/ccc.txt /opt/client/ccc.dfs 胜多负少的"patter1"\/.\.\w" print(findall(patter1, str))""" [/opt/client/ccc.txt /opt/client/ccc…...
.NET SignalR Redis实时Web应用
环境 Win10 VS2022 .NET8 Docker Redis 前言 什么是 SignalR? ASP.NET Core SignalR 是一个开放源代码库,可用于简化向应用添加实时 Web 功能。 实时 Web 功能使服务器端代码能够将内容推送到客户端。 适合 SignalR 的候选项: 需要从服…...

【热门话题】常见分类算法解析
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 常见分类算法解析1. 逻辑回归(Logistic Regression)2. 朴…...

有效利用MRP能为中小企业带来什么?
在离散制造企业,主流的生产模式主要为面向订单生产和面向库存生产(又称为预测生产),在中小企业中,一般为面向订单生产,也有部分面向库存和面向订单混合的生产方式(以面向订单为主,面…...

InternlM2
第一次作业 基础作业 进阶作业 1. hugging face下载 2. 部署 首先,从github上git clone仓库 https://github.com/InternLM/InternLM-XComposer.git然后里面的指引安装环境...

2024-12.python高级语法
异常处理 首先我们要理解什么叫做**"异常”**? 在程序运行过程中,总会遇到各种各样的问题和错误。有些错误是我们编写代码时自己造成的: 比如语法错误、调用错误,甚至逻辑错误。 还有一些错误,则是不可预料的错误…...
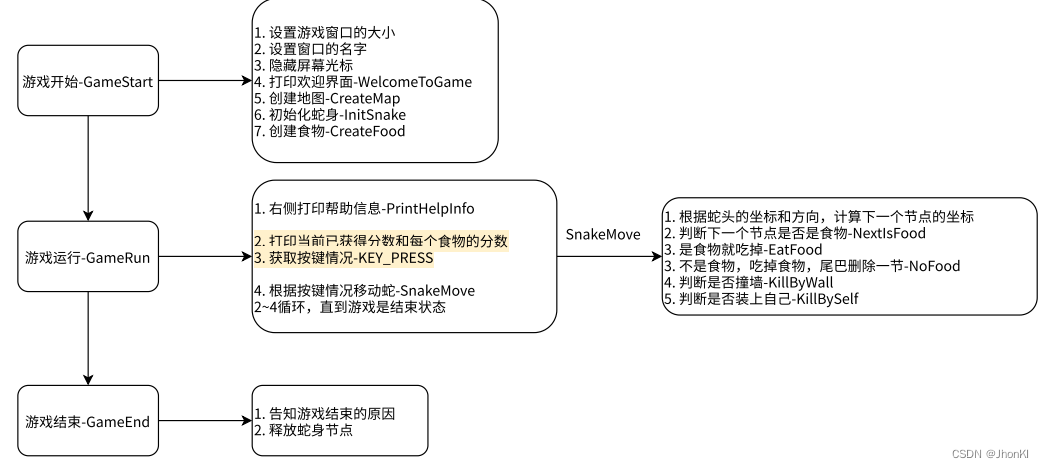
【C语言】贪吃蛇项目(1) - 部分Win32 API详解 及 贪吃蛇项目思路
文章目录 一、贪吃蛇项目需要实现的基本功能二、Win32 API介绍2.1 控制台2.2 部分控制台命令及调用函数mode 和 title 命令COORD 命令GetStdHandle(获取数据)GetConsoleCursorInfo(获取光标数据)SetConsoleCursorInfo (…...

秋叶Stable diffusion的创世工具安装-带安装包链接
来自B站up秋葉aaaki,近期发布了Stable Diffusion整合包v4.7版本,一键在本地部署Stable Diffusion!! 适用于零基础想要使用AI绘画的小伙伴~本整合包支持SDXL,预装多种必须模型。无需安装git、python、cuda等任何内容&am…...
华为ensp中aaa(3a)实现telnet远程连接认证配置命令
作者主页:点击! ENSP专栏:点击! 创作时间:2024年4月14日18点49分 AAA认证的全称是Authentication、Authorization、Accounting,中文意思是认证、授权、计费。 以下是详细解释 认证(Authentic…...

前端网络---http协议和https协议的区别
http协议和https的区别 1、http是超文本传输协议,信息是明文传输,https则是具有安全性的ssl加密传输协议。 2、http和https使用的端口不一样,http是80,https是443。 3、http的连接很简单,是无状态的(可以…...

FactoryMethod工厂方法模式详解
目录 模式定义实现方式简单工厂工厂方法主要优点 应用场景源码中的应用 模式定义 定义一个用于创建对象的接口,让子类决定实例化哪一个类。 Factory Method 使得一个类的实例化延迟到子类。 实现方式 简单工厂 以下示例非设计模式,仅为编码的一种规…...
)
Java基础-知识点1(面试|学习)
Java基础-知识点1 Java与C、PythonJava :C:Python: java 与 C的异同相似之处:区别: Java8的新特性Lambda 表达式:Stream API:接口的默认方法和静态方法: 基本数据类型包装类自动装箱与自动拆箱自…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

Ansible+Zabbix-agent2快速实现对多主机监控
ansible Ansible 是一款开源的自动化工具,用于配置管理(Configuration Management)、应用部署(Application Deployment)、任务自动化(Task Automation)和编排(Orchestration…...
