剑指 Offer 61 扑克牌中的顺子
摘要
扑克牌中的顺子
一、集合 Set + 遍历
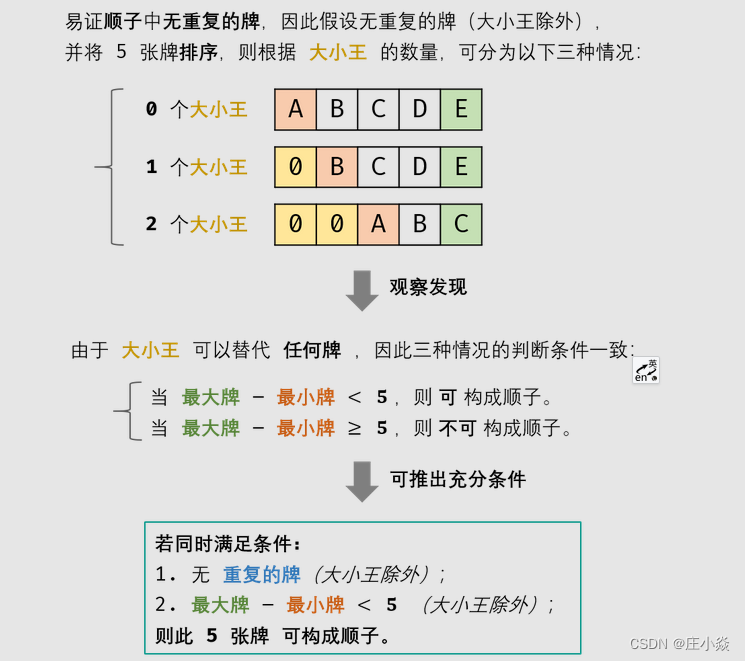
根据题意,此5张牌是顺子的 充分条件 如下:
- 除大小王外,所有牌 无重复 ;
- 设此5张牌中最大的牌为max,最小的牌为min(大小王除外),则需满足:max−min<5。
因而,可将问题转化为:此5张牌是否满足以上两个条件?
算法步骤:
- 遍历五张牌,遇到大小王(即0)直接跳过。
- 判别重复:利用 Set 实现遍历判重, Set 的查找方法的时间复杂度为O(1);
- 获取最大 / 最小的牌: 借助辅助变量 max和min,遍历统计即可。
class Solution {public boolean isStraight(int[] nums) {Set<Integer> repeat = new HashSet<>();int max = 0, min = 14;for(int num : nums) {if(num == 0) continue; // 跳过大小王max = Math.max(max, num); // 最大牌min = Math.min(min, num); // 最小牌if(repeat.contains(num)) return false; // 若有重复,提前返回 falserepeat.add(num); // 添加此牌至 Set}return max - min < 5; // 最大牌 - 最小牌 < 5 则可构成顺子}
}复杂度分析:
- 时间复杂度 O(N)=O(5)=O(1) : 其中 N为nums长度,本题中N≡5;遍历数组使用O(N)时间。
- 空间复杂度 O(N)=O(5)=O(1): 用于判重的辅助 Set 使用 O(N) 额外空间
二、排序 + 遍历
- 先对数组执行排序。
- 判别重复: 排序数组中的相同元素位置相邻,因此可通过遍历数组,判断 nums[i]=nums[i+1]是否成立来判重。
- 获取最大 / 最小的牌: 排序后,数组末位元素nums[4]为最大牌;元素 nums[joker]为最小牌,其中 joker为大小王的数量。
package Hashmap;import java.util.Arrays;/*** @Classname JZ61扑克牌中的顺子* @Description TODO* @Date 2023/3/7 21:43* @Created by xjl*/
public class JZ61扑克牌中的顺子 {public boolean isStraight(int[] nums) {int joker = 0;Arrays.sort(nums); // 数组排序for(int i = 0; i < 4; i++) {if(nums[i] == 0) {joker++; // 统计大小王数量}else if(nums[i] == nums[i + 1]) {return false; // 若有重复,提前返回 false}}return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子}
}
复杂度分析:
-
时间复杂度 O(NlogN)=O(5log5)=O(1): 其中 NN 为nums长度,本题中N≡5;数组排序使用 O(NlogN)时间。
- 空间复杂度 O(1): 变量 jokerjoker 使用 O(1)大小的额外空间。
博文参考
《leetcode》
相关文章:

剑指 Offer 61 扑克牌中的顺子
摘要 扑克牌中的顺子 一、集合 Set 遍历 根据题意,此5张牌是顺子的 充分条件 如下: 除大小王外,所有牌 无重复 ;设此5张牌中最大的牌为max,最小的牌为min(大小王除外),则需满足…...
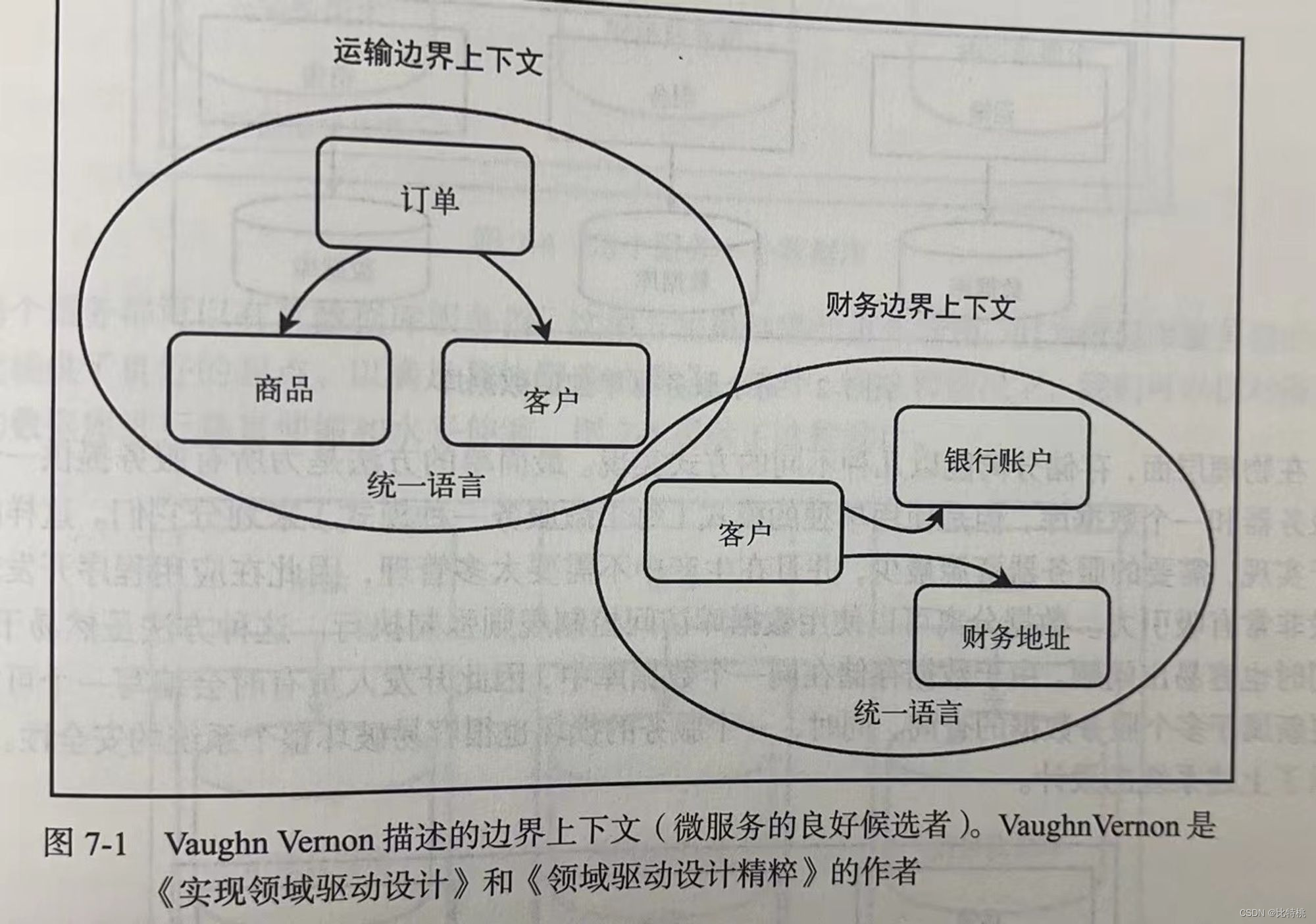
Spring 响应式编程-读书笔记
序言 大家好,我是比特桃。本文为《Spring 响应式编程》的读书笔记,响应式技术栈可以创建极其高效、易于获取且具有回弹性的端点,同时响应式可以容忍网络延迟,并以影响较小的方式处理故障。响应式微服务还可以隔离慢速事务并加速速…...
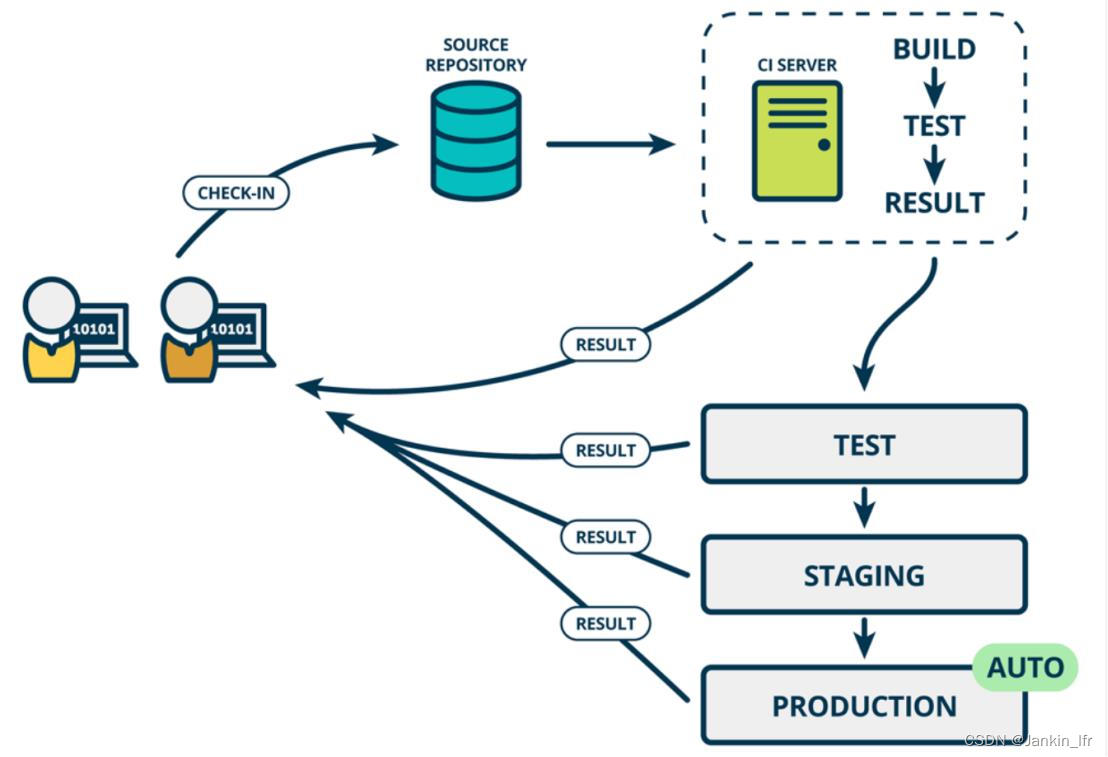
CI流水线的理解
一、概念 单元测试:针对软件的基本单元(如:类、函数)所做的测试。 集成测试:将软件代码单元集成起来后,以组件、模块和子系统为单位进行的测试,主要测试接口间的交互关系。也称组件测试…...
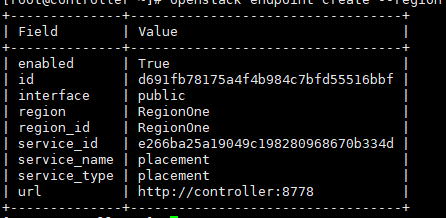
OpenStack手动分布式部署Nova【Queens版】
目录 Nove简介: 1、登录数据库配置(在controller执行) 1.1登录数据库 1.2数据库里创建nova-api 1.3数据库登录授权 1.4创建nova用户 1.5添加admin用户为nova用户 1.6创建nova服务端点 1.7创建compute API 服务端点 1.8创建一个placement服务…...

centos7 oracle19c安装 ORA-01012: not logged on
总共分三步 1.下载安装包:里面有一份详细的安装教程 链接:https://pan.baidu.com/s/1Of2a72pNLZ-DDIWKrTQfLw?pwd8NAx 提取码:8NAx 2.安装后,执行初始化:时间较长 /etc/init.d/oracledb_ORCLCDB-19c configure 3.配置环境变量,不配置环境变量,sq…...

山东小巨人申报条件
国家专精特新小巨人特点1、经济效益:上年度企业营业收入在1亿元至4亿元之间,近2年主营业务收入或净利润的平均增长率达到10%以上,企业资产负债率不高于70%。2、专业化程度:(1)企业从事特定细分市场时间达到…...

手写中实现并学习ahooks——useRequest
前言 最近业务没有之前紧张了,也是消失了一段时间,也总结了一些之前业务上的问题。 和同事沟通也是发现普通的async await 封装api在复杂业务场景下针对于请求的业务逻辑比较多,也是推荐我去学习一波ahooks,由于问题起源于请求…...

[手写OS]动手实现一个OS 之 准备工作以及引导扇区
[手写OS]动手实现一个OS之第一步-环境以及引导扇区 环境准备 一台可用计算机(linux我不知道,我用的Windows)汇编编译器NASM一个方便的软盘读写工具VirtualBox 汇编编译器NASM 官网地址:https://www.nasm.us/pub/nasm/snapshot…...

JVM实战OutOfMemoryError异常
目录 Java堆溢出 常见原因: 虚拟机栈和本地方法栈溢出 实验1:虚拟机栈和本地方法栈测试(作为第1点测试程序) 实验2:(作为第1点测试程序) 运行时常量池和方法区溢出 运行时常量池内存溢出 …...

C++虚函数操作指南
1 什么是虚函数?1.1 虚函数的使用规则1.2 用 C 运行虚函数的示例1.3 协变式返回类型2 在 C 中使用虚函数的优点2.1 代码更为灵活、更为通用2.2 代码可复用2.3 契约式设计3 虚函数的局限性3.1 性能3.2 设计问题3.3 调试,容易出错4 虚函数的替代方案4.1 仅…...

Mybatis-Plus分页插件
引言:MyBatis Plus自带分页插件,只要简单的配置即可实现分页功能 1.添加Configuration配置类 Configuration MapperScan("com.atguigu.mybatisplus.mapper") //可以将主类中的注解移到此处public class MybatisPlusConfig {Beanpublic Mybatis…...

Selenium Webdriver options的实用参数设置
1、关闭Chrome浏览器受自动控制的提示 options.add_experimental_option(useAutomationExtension, False) options.add_experimental_option(excludeSwitches, [enable-automation])2、关闭是否保存密码的弹窗 options.add_experimental_option("prefs", { "c…...

代码随想录算法训练营第七天|454.四数相加II 、 383. 赎金信 、 15. 三数之和 、18. 四数之和
454.四数相加II 454.四数相加II介绍给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:思路因为是存放在数组里不同位置的元素,因此不需要考虑去重的操作,而…...

详解抓包原理以及抓包工具whistle的用法
什么是抓包? 分析网络问题业务分析分析网络信息流通量网络大数据金融风险控制探测企图入侵网络的攻击探测由内部和外部的用户滥用网络资源探测网络入侵后的影响监测链接互联网宽频流量监测网络使用流量(包括内部用户,外部用户和系统)监测互联网和用户电脑的安全状…...
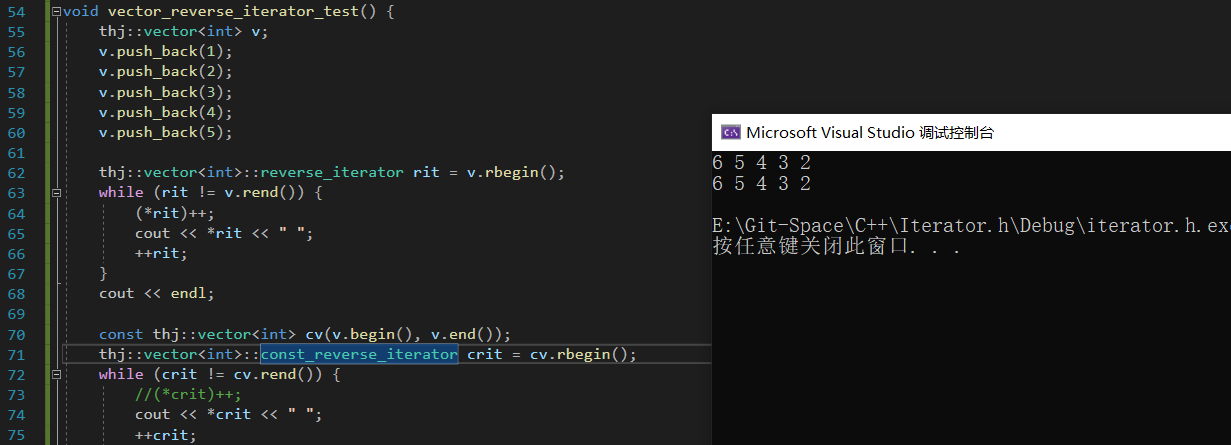
【C++】反向迭代器
文章目录一、什么是反向迭代器二、STL 源码中反向迭代器的实现三、reverse_iterator 的模拟实现四、vector 和 list 反向迭代器的实现一、什么是反向迭代器 C 中一共有四种迭代器 – iterator、const_iterator、reverse_iterator 以及 const_reverse_iterator,其中…...

(蓝桥真题)扫描游戏(计算几何+线段树二分)
题目链接:P8777 [蓝桥杯 2022 省 A] 扫描游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 5 2 0 1 1 0 3 2 4 3 5 6 8 1 -51 -33 2 样例输出: 1 1 3 4 -1 分析:先考虑如何对物件进行排序,首先&…...
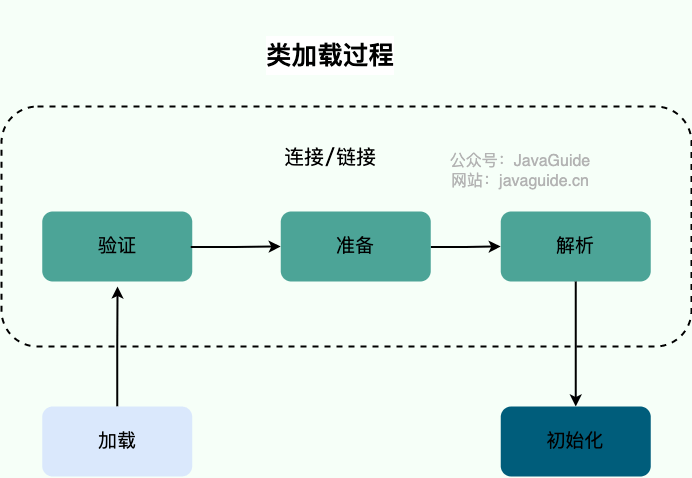
面试官:什么是双亲委派模型?如何打破它?
本文已经收录进 JavaGuide(「Java学习+面试指南」一份涵盖大部分 Java 程序员所需要掌握的核心知识。) 参加过校招面试的同学,应该对这个问题不陌生。一般提问 JVM 知识点的时候,就会顺带问你双亲委派模型(别扭的翻译。。。)。 就算是不准备面试,学习双亲委派模型对于我…...
自建服务器系列- DDNS配置
1、环境说明 光猫桥接路由器拔号的模式 2、DDNS是什么 对于DHCP方式获得的IP,无论对于局域网内来说,还是外网来说,都会有使得IP地址每隔一段时间变化一次,如果想要通过恒定不变的地址访问主机,就需要动态域名解析。…...

vue中使用axios简单封装用法,axios报错the request was rejected because no multipart boundar
在这里插入代码片## 创建实例 //这个写法作为我错误的记录,可以不看暂时 transformRequest: [(data: any) > {if (!data) {data {}}return qs.stringify(data)}]在我的项目里面,初始化配置里面进行handers的修改,例如:例如将…...

Leetcode.1220 统计元音字母序列的数目
题目链接 Leetcode.1220 统计元音字母序列的数目 Rating : 1730 题目描述 给你一个整数 n,请你帮忙统计一下我们可以按下述规则形成多少个长度为 n的字符串: 字符串中的每个字符都应当是小写元音字母(a, e, i, o, u)…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
