vue 一键更换主题颜色
这里提供简单的实现步骤,具体看自己怎么加到项目中
我展示的是vue2 vue3同理

在 App.vue 添加 入口处直接修改
#app { // 定义的全局修改颜色变量--themeColor:#008cff;
}
// 组件某些背景颜色需要跟着一起改变,其他也是同理
/deep/ .ant-btn-primary{background-color: var(--themeColor);
}
在某个页面,写一个方法或者是颜色选择器,提供修改的颜色

updColor () {// 修改app下的 这个变量 这个颜色document.getElementById('app').style.setProperty('--themeColor', 'red')},
如果是单页面修改的颜色,或者是单个地方使用, 直接这样修改就可以了
<style lang="less" scoped>.wrapper{background-color: var(--themeColor);}
</style>
如果要实现保留修改颜色记录,可以放到vuex或者缓存去加载
相关文章:

vue 一键更换主题颜色
这里提供简单的实现步骤,具体看自己怎么加到项目中 我展示的是vue2 vue3同理 在 App.vue 添加 入口处直接修改 #app { // 定义的全局修改颜色变量--themeColor:#008cff; } // 组件某些背景颜色需要跟着一起改变,其他也是同理 /deep/ .ant-btn-primar…...
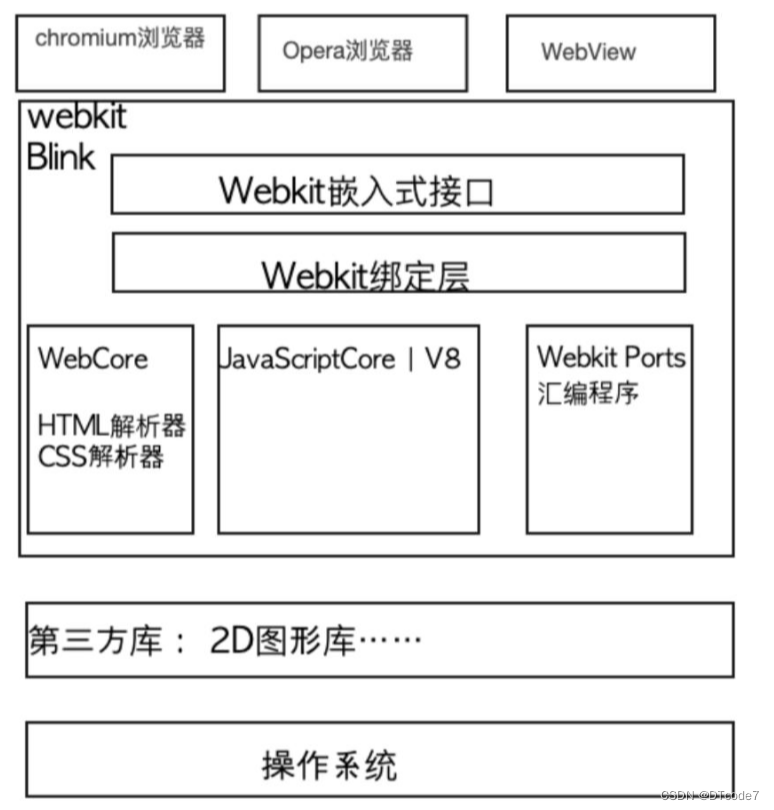
WebKit内核游览器
WebKit内核游览器 基础概念游览器引擎Chromium 浏览器架构Webkit 资源加载这里就不得不提到http超文本传输协议这个概念了: 游览器多线程HTML 解析总结 基础概念 百度百科介绍 WebKit 是一个开源的浏览器引擎,与之相对应的引擎有Gecko(Mozil…...
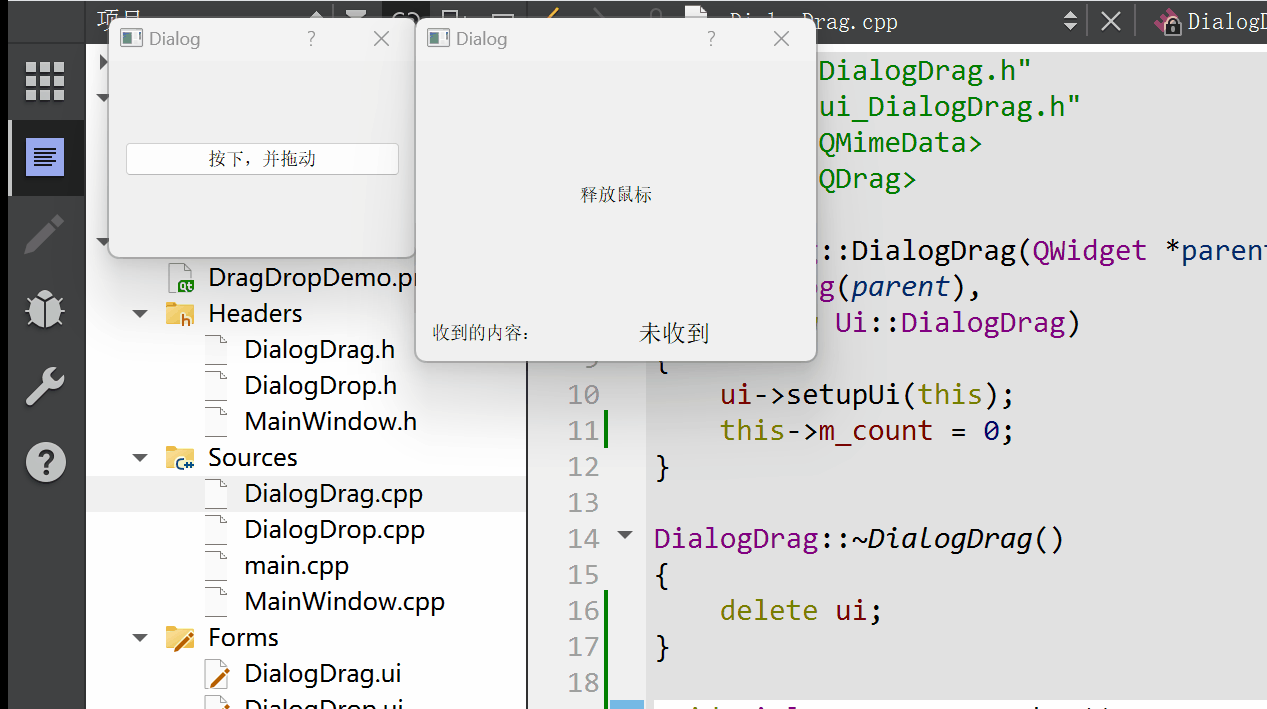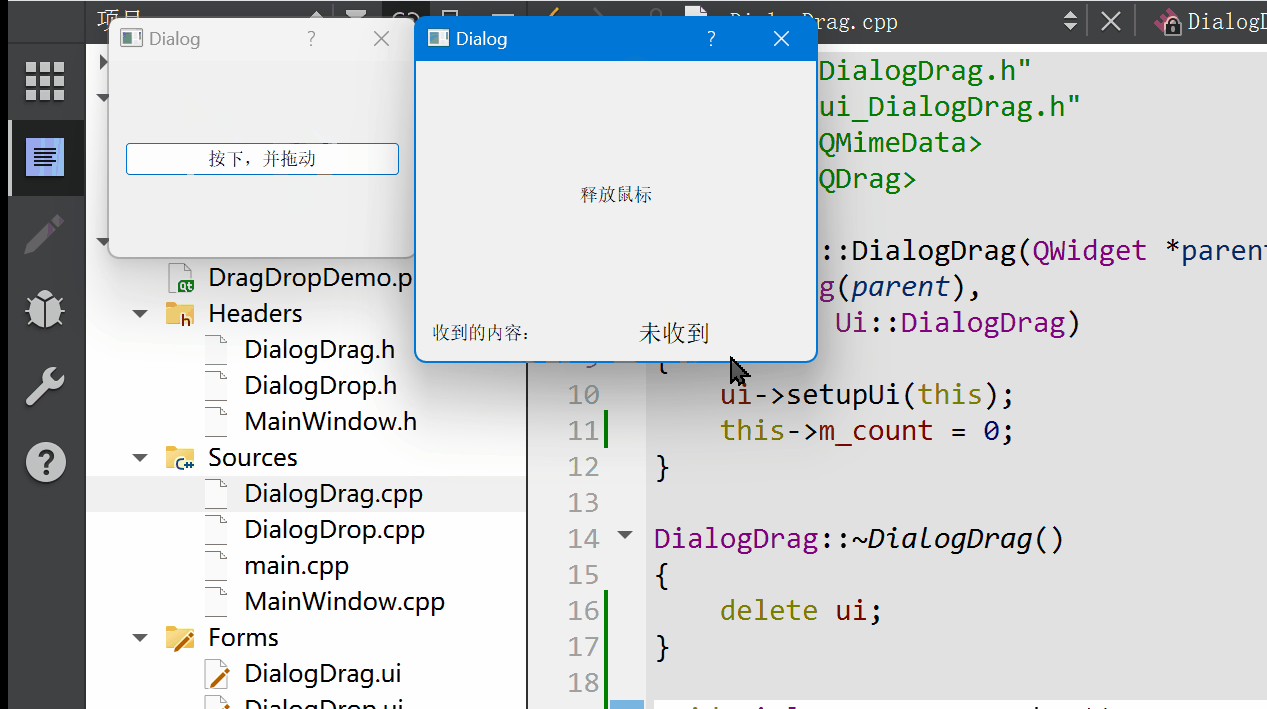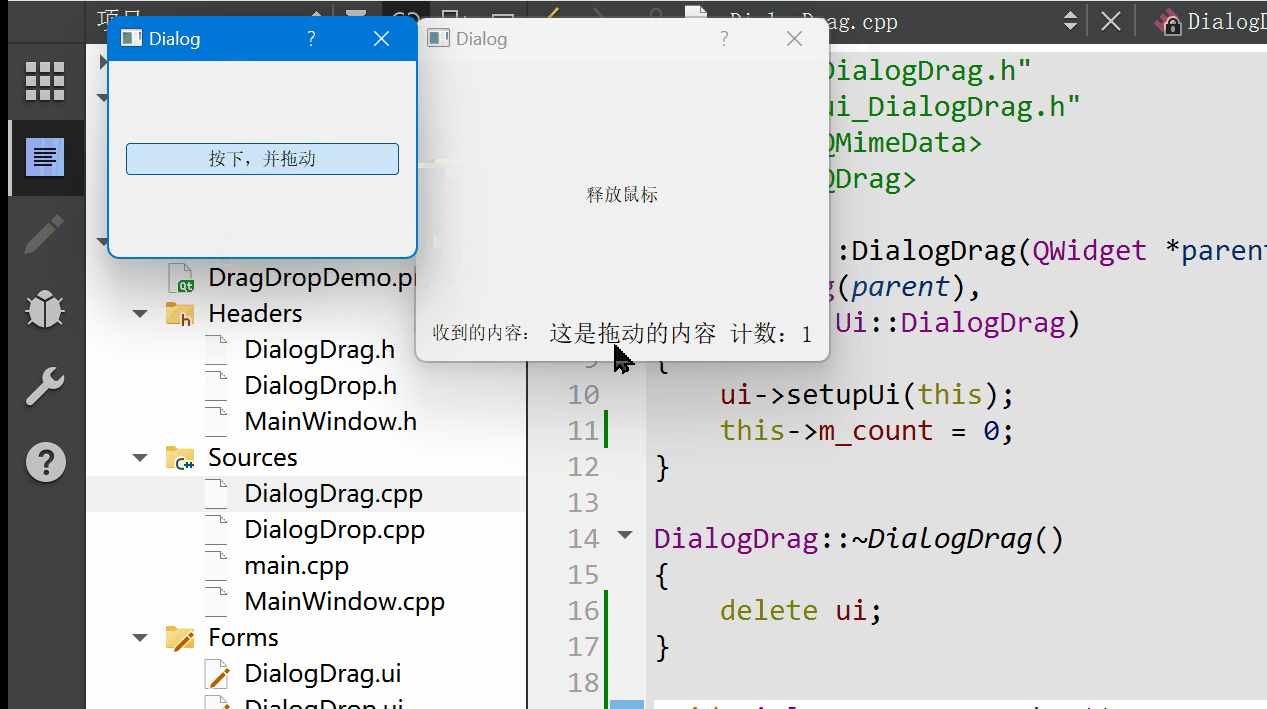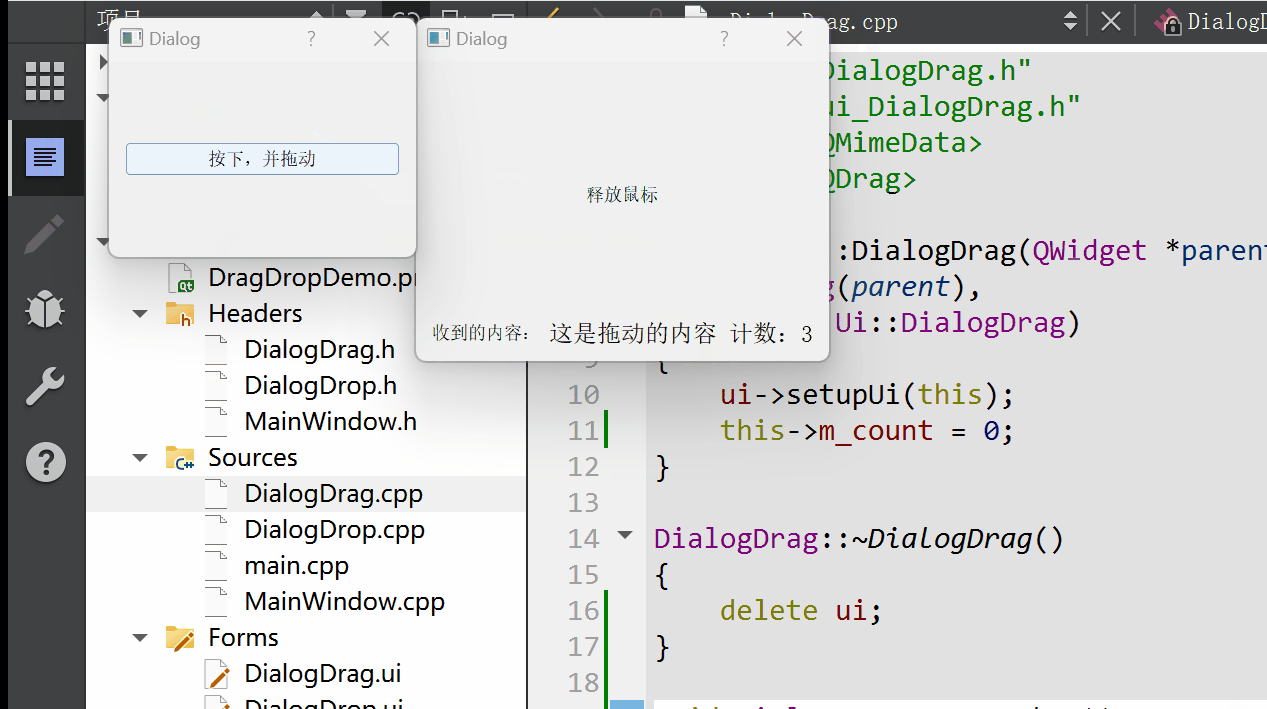
Qt 拖放功能详解:理论与实践并举的深度指南
拖放(Drag and Drop)作为一种直观且高效的用户交互方式,在现代图形用户界面中扮演着重要角色。Qt 框架提供了完善的拖放支持,允许开发者在应用程序中轻松实现这一功能。本篇博文将详细阐述Qt拖放机制的工作原理,结合详…...
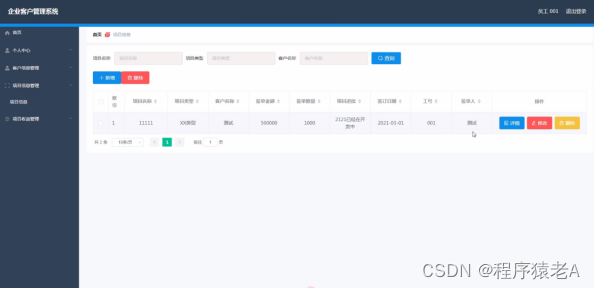
Springboot+Vue项目-基于Java+MySQL的企业客户管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...
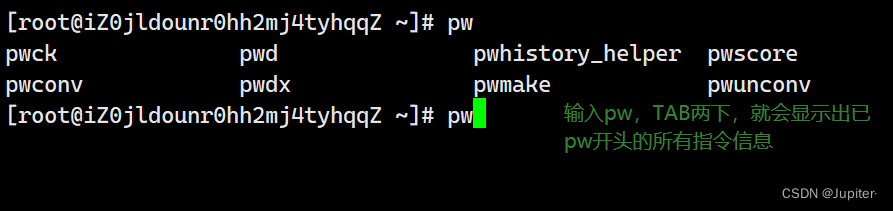
【Linux学习】Linux指令(四)
文章标题 🚀zip/unzip指令:🚀tar指令(重要):🚀uname –r指令:🚀关机指令🚀几个常用操作 🚀zip/unzip指令: zip 与 unzip的安装 yum i…...
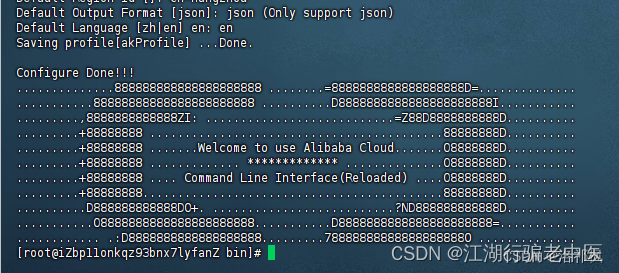
阿里云服务器 使用Certbot申请免费 HTTPS 证书及自动续期
前言 Certbot是一款免费且开源的自动化安全证书管理工具,由电子前沿基金会(EFF)开发和维护,是在Linux、Apache和Nginx服务器上配置和管理SSL/TLS证书的一种机制。Certbot可以自动完成域名的认证并安装证书。 一、 安装软件 1.1…...

统一SQL-number/decimal/dec/numeric转换
统一SQL介绍 https://www.light-pg.com/docs/LTSQL/current/index.html 源和目标 源数据库:Oracle 目标数据库:Postgresql,TDSQL-MySQL,达梦8,LightDB-Oracle 操作目标 通过统一SQL,将Oracle中的numb…...
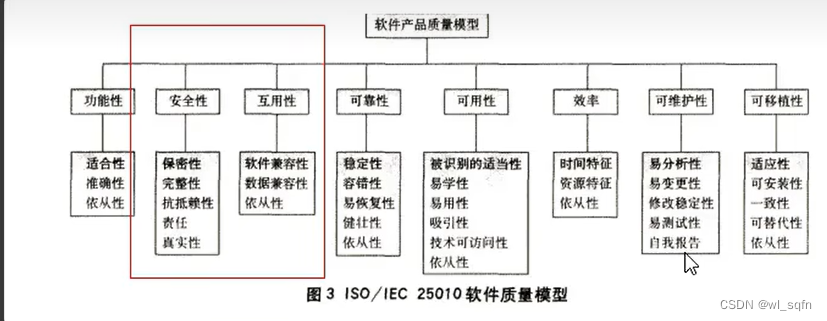
软件测试入门学习笔记
系统测试流程规范 一.研发模型 1.瀑布模型 从可行性研究(或系统分析)开始,需求 2.增量迭代模型 3.敏捷开发模型 二.质量模型...

31. 下一个排列
题目描述 整数数组的一个排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地&…...

Android笔记: mkdirs不生效失败
Manifest已经配置权限,代码中也动态获取权限,mkdirs一直返回false File.mkdirs()方法创建文件夹失败 1、动态申请读写权限 <!--SDCard写权限--> <uses-permission android:name="android.permission.WRITE_EXTERNAL_STORAGE" /> <!--SDCard读权…...
——贪心+构造)
需要添加的硬币的最小数量(Lc2952)——贪心+构造
给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值,以及一个整数 target 。 如果存在某个 coins 的子序列总和为 x,那么整数 x 就是一个 可取得的金额 。 返回需要添加到数组中的 任意面值 硬币的 最小数量 ,使范围 …...

军工保密资质介绍及申请要求
军工保密资质介绍 军工保密资质是指国家对从事军工研发、生产、销售等活动的企事业单位进行的一种资质认证。该资质的核心目标是保护国家军事机密和军事技术秘密,确保国家安全和国防利益。军工保密资质的认证标准非常严格,涉及企业的安全管理、技术保密…...

ES6的编程风格
ES6 提出了两个新的声明变量的命令:let和const。其中,let完全可以取代var,因为两者语义相同,而且let没有副作用。 var命令存在变量提升效用,let命令没有这个问题 if (true) {console.log(x); // ReferenceErrorlet x…...
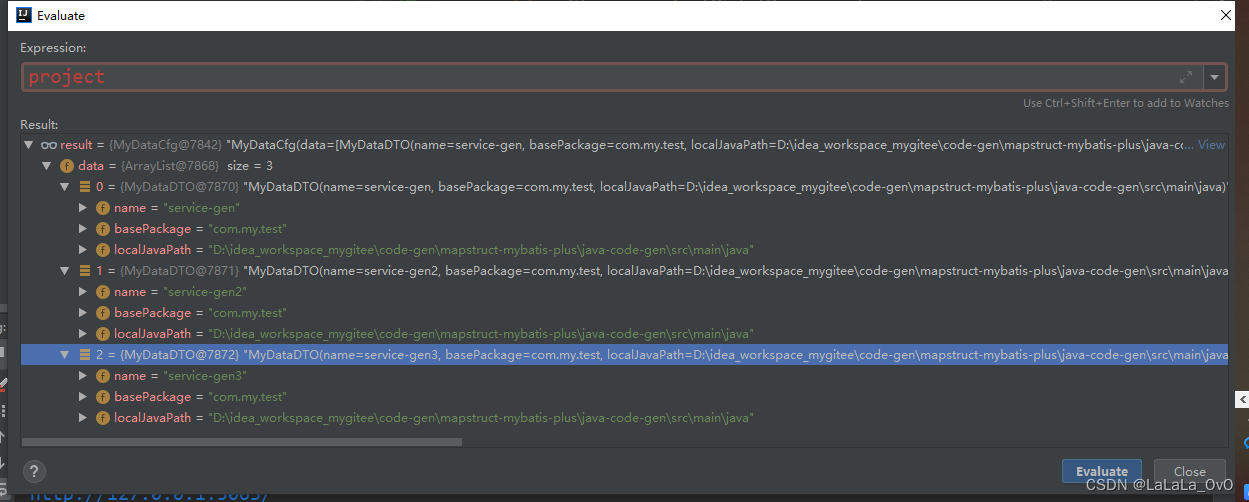
springboot 载入自定义的yml文件转DTO
json解析的pom引入 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-json</artifactId><version>5.8.20</version></dependency>resources目录下的my-data.yml project:data:- name: service-genbase-package:…...

webpack-(plugin,本地服务器,路径别名,安装vue)
安装vue npm i vue-loader -D npm i vue 编写一个vue文件: 在index.html中设置 一个id为app的div 将vue文件挂载到app中 vue比较特殊,除了使用loader外,还使用了plugin const path require("path"); const { VueLoaderPlugin …...

http请求头导致了dial tcp:lookup xxxx on 10.43.0.10:53 no sunch host
事实证明人有的时候也不能太偷懒,太偷懒容易给自己埋坑。 问题的背景: web端调用服务A,服务A异步调用服务B。服务A有四个场景需要调用服务B,所以,服务A中封装了一个公用的方法,唯一的区别是,场…...

想要设计放大电路,必须掌握哪些?
放大电路是电子系统中的核心组成部分,其设计好坏将直接影响到整个系统的性能,对电子工程师来说,在设计放大电路时,必须掌握且关注多方面,以此确保电路的稳定性和放大效果,那么需要注意哪些? 1、…...
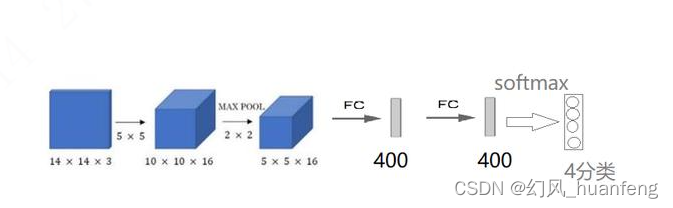
每天五分钟计算机视觉:基于卷积操作完成滑动窗口的图片分类?
本文重点 我们前面学习了使用不同大小的滑动窗口来滑动图片,然后切分成许多小的图片,然后依次应用到我们已经训练好的图像分类模型中,但是这种方式效率太低了,本节课程我们学习一种新的方式,来看一下如何并行识别这些剪切的图片。 原始结构 首先我们先来看一下,如何把…...

UI设计/交互设计/视觉设计项目汇报/作品集Figma/PPT模板
作为UI设计/交互设计/视觉设计师,创建作品集对于向潜在客户或雇主展示您的技能、创造力和风格至关重要。以下分步指南可帮助您创建令人印象深刻的作品集: 选择您的最佳作品:选择您最强大且最相关的设计项目,将其纳入您的作品集。…...
)
25、Lua 学习笔记之三(高阶话题)
Lua 学习笔记之三 高阶话题迭代实例代码有关迭代的描述 协作线程实例代码有关协作线程的描述 高阶话题 迭代 实例代码 --迭代 local function enum(array)local index 1return function()local ret array[index]index index 1return retend endlocal function foreach(a…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
