算法--贪心算法
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。贪心算法在有最优子结构的问题中尤其有效,这意味着局部最优解能决定全局最优解。简单来说,贪心算法对每个子问题都做出选择,不能回退,这与动态规划不同,后者会保存以前的结果,并根据以前的结果对当前进行选择,有回退功能。
贪心算法的特点:
- 局部最优选择:在每一步都做出在当前看来最优的选择,希望这些局部最优能导致全局最优解。
- 无回退操作:一旦做出了选择,就不再回退,即不考虑以前的选择。
贪心算法适用的问题:
贪心算法适用于具有“贪心选择性质”的问题,即局部最优解能决定全局最优解。贪心算法不能保证求得的最后解是最佳的,也不能用来求最大或最小解的问题,只能求满足某些约束条件的可行解的范围。
贪心算法的应用实例包括:
- 找零问题:如何用最少的硬币找零。
- 最小生成树:如Kruskal算法和Prim算法。
- 单源最短路径:如Dijkstra算法。
- 任务调度问题:如何安排任务以减少等待时间或延迟。
- 压缩编码:如Huffman编码。
贪心算法的设计步骤:
- 建立数学模型来描述问题。
- 把求解的问题分成若干个子问题。
- 对每一子问题求解,得到子问题的局部最优解。
- 把子问题的解局部最优解合成原来解问题的一个解。
虽然贪心算法相对简单易懂,但它并不总是能得到全局最优解,因此在使用时需要仔细分析问题是否适合采用贪心算法。
贪心算法可以用来解决背包问题的一种特殊形式——分数背包问题(Fractional Knapsack Problem),但对于经典的0-1背包问题,贪心算法通常无法保证找到最优解。
分数背包问题
在分数背包问题中,你可以将物品分割成任意大小,然后选择其中的一部分放入背包中,目标是最大化背包中物品的总价值,同时不超过背包的容量限制。对于这个问题,贪心算法是有效的,因为你可以按照物品的价值重量比(单位价值)来选择物品,优先选择单位价值最高的物品,直到背包装满为止。
0-1背包问题
对于0-1背包问题,每个物品只能整体选取或不选取,不能分割。这种情况下,贪心算法选择物品的策略可能无法得到最优解。例如,如果贪心算法只考虑物品的价值或重量,而不是价值重量比,那么它可能会错过更优的组合,因为一个轻而价值高的物品可能比几个重而价值低的物品更有价值。
对于0-1背包问题,最优解可能需要通过动态规划等方法来找到,因为贪心算法可能无法考虑到所有物品组合的总价值。
总结,贪心算法适用于分数背包问题,但对于0-1背包问题,它可能无法保证找到最优解。
以下是使用贪心算法解决分数背包问题的C语言实现。在这个实现中,我们首先根据物品的价值重量比(单位价值)对物品进行排序,然后按单位价值从高到低依次选择物品放入背包,直到背包容量达到限制。
#include <stdio.h>
#include <stdlib.h>// 定义物品结构体
typedef struct {float weight; // 物品重量float value; // 物品价值float ratio; // 价值重量比
} Item;// 比较函数,用于排序
int compare(const void *s1, const void *s2) {Item *e1 = (Item *)s1;Item *e2 = (Item *)s2;return e2->ratio - e1->ratio > 0 ? 1 : -1; // 降序排序
}// 贪心算法解决分数背包问题
float fractionalKnapsack(int W, Item arr[], int n) {// 按价值重量比排序qsort(arr, n, sizeof(arr[0]), compare);int curWeight = 0; // 当前背包重量float finalvalue = 0.0; // 结果(总价值)// 遍历所有物品for (int i = 0; i < n; i++) {// 如果加入当前物品不超过最大重量,加入整个物品if (curWeight + arr[i].weight <= W) {curWeight += arr[i].weight;finalvalue += arr[i].value;} else {// 如果不能加入整个物品,加入背包能装下的部分int remain = W - curWeight;finalvalue += arr[i].value * ((float) remain / arr[i].weight);break; // 背包已满}}return finalvalue;
}// 测试代码
int main() {int W = 50; // 背包容量Item arr[] = {{10, 60}, {20, 100}, {30, 120}};int n = sizeof(arr) / sizeof(arr[0]);printf("最大价值为: %.2f", fractionalKnapsack(W, arr, n));return 0;
}
这段代码首先定义了一个Item结构体来存储每个物品的重量、价值和价值重量比。compare函数用于根据价值重量比对物品进行降序排序。fractionalKnapsack函数实现了贪心算法,首先对物品按价值重量比进行排序,然后遍历排序后的物品数组,根据背包剩余容量决定是否将当前物品整个或部分加入背包。最后,函数返回背包中物品的最大总价值。
相关文章:

算法--贪心算法
贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。贪心算法在有最优子结构的问题中尤其有效,这意味着局部最优解能决定全局最优解。简单来说,贪心…...

Redis基本數據結構 ― String
Redis基本數據結構 ― String 介紹常用命令範例1. 為字串鍵設值/取得字串鍵的值2. 查看字串鍵的過期時間3. 如何為key設置時間?4. 如何刪除指定key?5. 如何增加value的值?6. 獲取value值的長度 介紹 字串鍵是Redis中最基本的鍵值對類型,這種類型的鍵值對會在數據…...

php7.4在foreach中对使用数据使用无法??[]判读,无法使用引用传递
代码如下图:这样子在foreach中是无法修改class_history的。正确的应该是去掉??[]判断。 public function actionY(){$array [name>aaa,class_history>[[class_name>一班,class_num>1],[class_name>二班,class_num>2]]];foreach ($array[class_…...
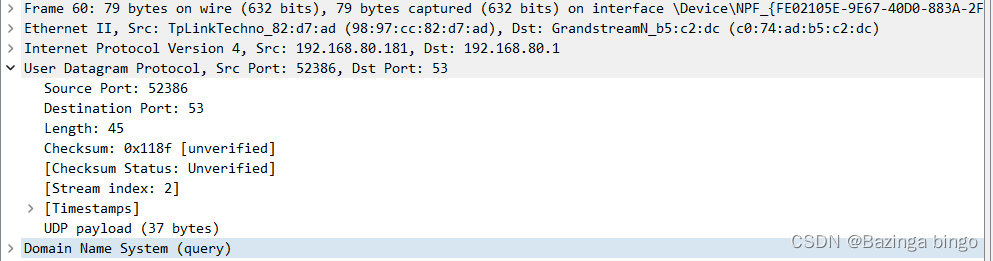
传输层协议 TCP UDP协议 解析(二)
文章目录 UDP:用户数据报协议UDP报文格式TCP与UDP的区别 UDP:用户数据报协议 UDP是一种面向无连接的传输层协议(数据一直发送,没有ack,所以不需要考虑ack),传输可靠性没有保证。 UDP不提供重传…...
)
java+jsp+Oracle+Tomcat 记账管理系统论文(一)
⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️ ➡️点击免费下载全套资料:源码、数据库、部署教程、论文、答辩ppt一条龙服务 ➡️有部署问题可私信联系 ⬆️⬆️⬆️⬆️…...
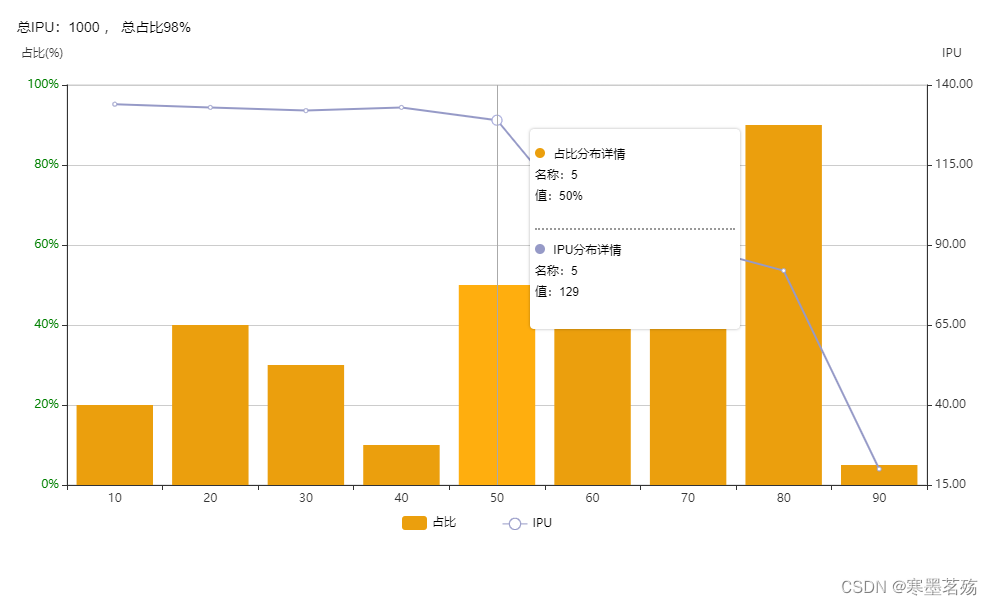
echarts双Y轴,并实现图例等
一个Y轴时yAxis为对象 yAxis: {type: value,name: 占比(%) },两个Y轴时yAxis为数组 yAxis: [{ // 左侧的type: value,name: 占比(%),nameTextStyle: {padding: [0, 0, 10, -50]},min: 0,max: 100,splitNumber: this.splitNumber, // 设置坐标轴的分割段数interval: 20, // 标轴…...
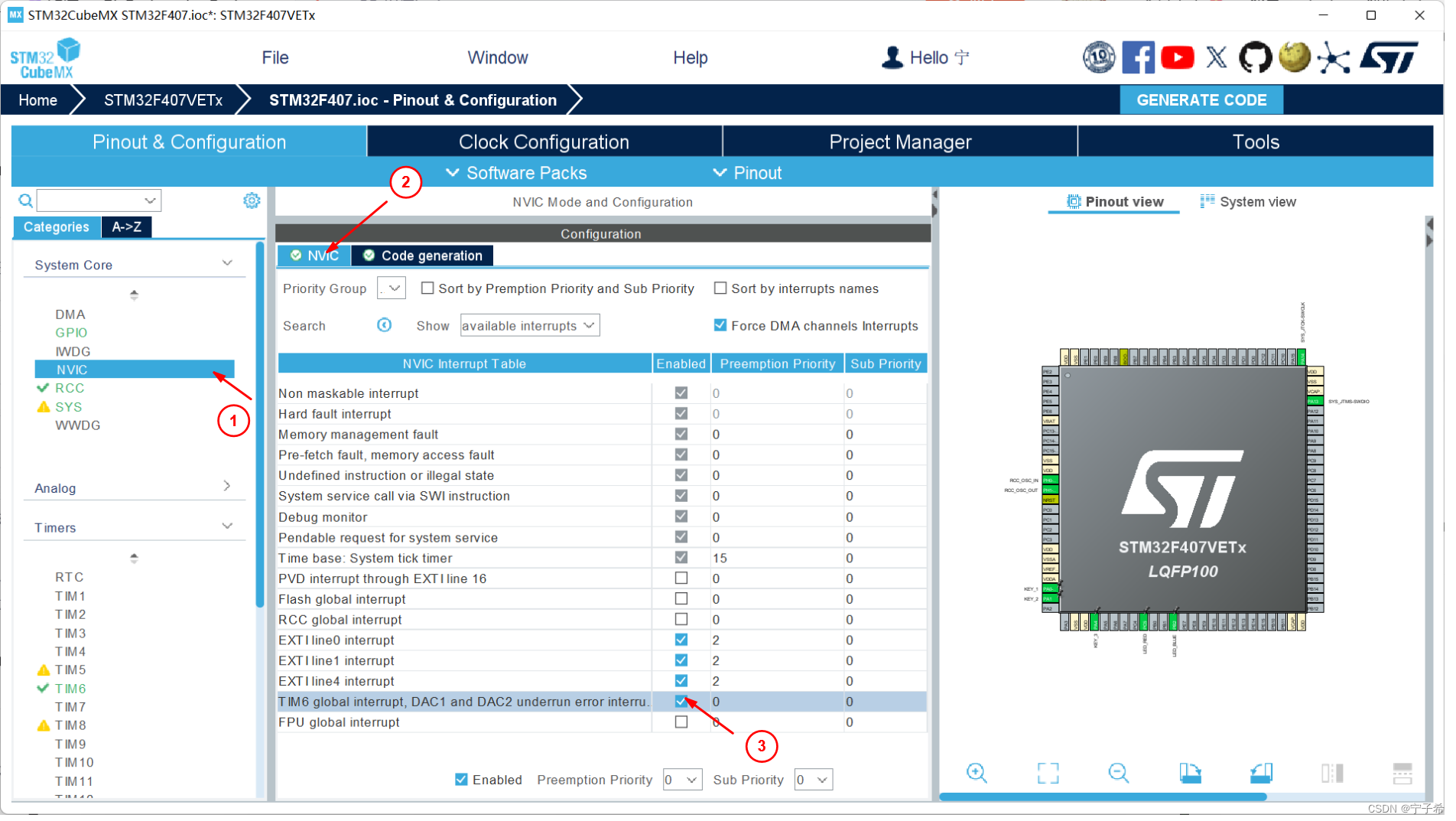
STM32 工程移植 LVGL:一步一步完成
STM32 工程移植 LVGL:一步一步完成 LVGL,作为一款强大且灵活的开源图形库,专为嵌入式系统GUI设计而生,极大地简化了开发者在创建美观用户界面时的工作。作为一名初学者,小编正逐步深入探索LVGL的奥秘,并决…...

Linux中分析日志及问题排查
可以参考:Linux命令 Linux系统日志是系统管理和故障排查的关键工具。通过分析系统日志,我们能够深入了解系统的运行状况,迅速发现并解决潜在的问题。 1. 日志文件位置 系统日志通常存储在/var/log/目录下,不同的日志有不同的文件,如下: /var/log/syslog:系统日志,包含…...

复杂环境下实时鲁棒3D激光雷达定位
复杂环境下实时鲁棒3D激光雷达定位 一、摘要 定位是机器人领域的重要研究方向。本篇文章里,我们提出了一种基于3D激光雷达的复杂环境下的定位方案。我们首先使用GPS和雷达建立一张点云地图,然后在匹配定位的时候从大地图中分割出一个小地图,…...
9.3.k8s的控制器资源(deployment部署控制器)
目录 一、deployment部署控制器概念 二、deployment资源的清单编写 三、小结 功能 使用场景 原理 四、deployment实现升级和回滚 1.编辑deployment资源清单(v1版本) 2.创建service资源用于访问 编辑 3.修改deploy清单中pod镜像版本为V2 4…...

通过符号程序搜索提升prompt工程
原文地址:supercharging-prompt-engineering-via-symbolic-program-search 通过自动探索大量提示变体来找到更好的提示 2024 年 4 月 22 日 众所周知,LLMs的成功在很大程度上仍然取决于我们用正确的指导和例子来提示他们的能力。随着新一代LLMs变得越…...

js开启子线程及其使用
众所周知,js是单线程,但是可以开启子线程来帮忙处理一些数据,但是这个子线程是有限制的 1.必须是同源 2.完全受主线程控制 3.不能在子线程中操作dom节点 4.子线程没有window,可以使用self 5.等等 具体的查看官网 进程切换是要耗时…...
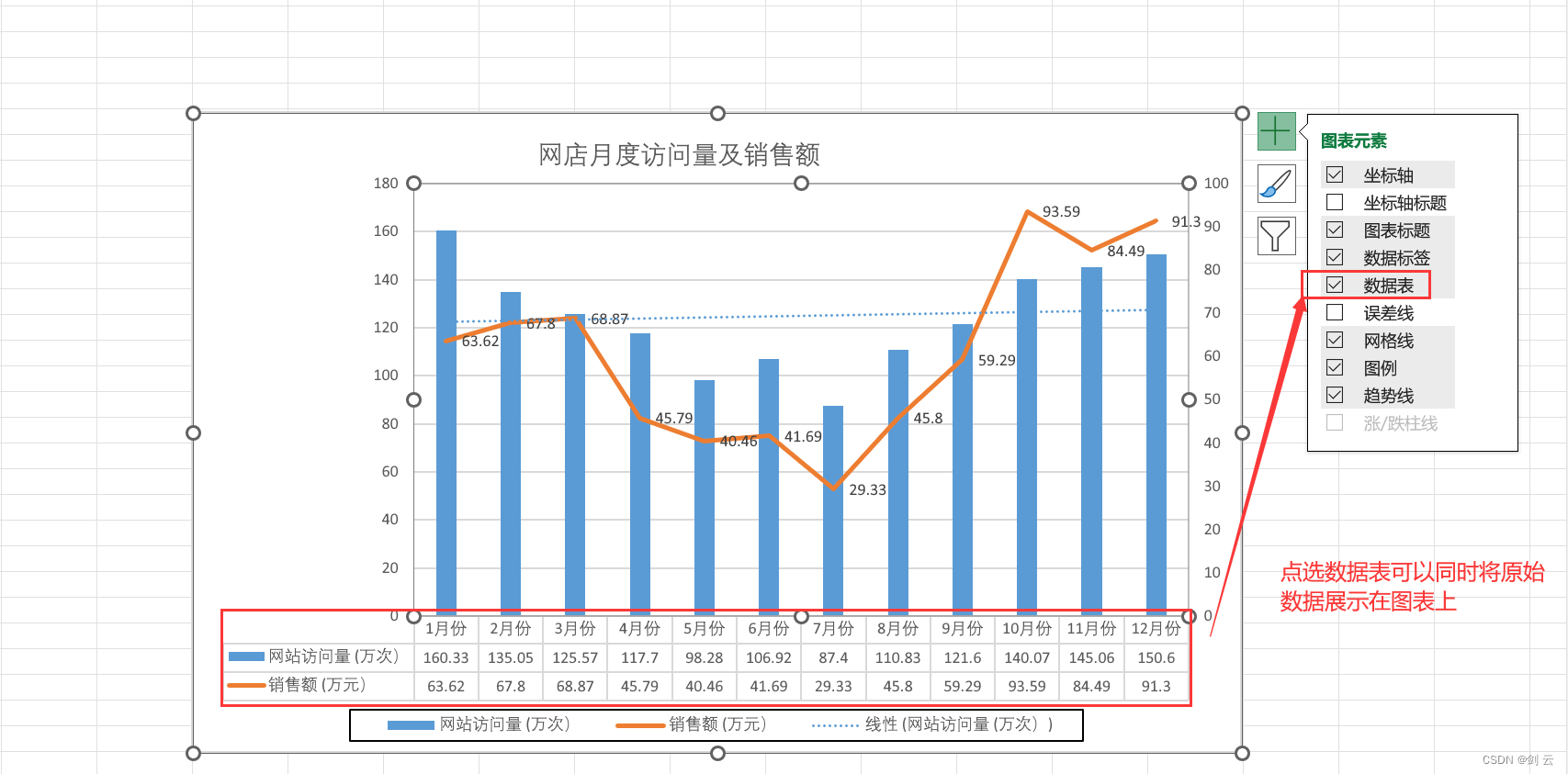
excel办公系列-图表元素及其作用
Excel图表元素及其作用 Excel图表由各种元素组成,每个元素都有其特定的作用,可以帮助我们更清晰地传达数据信息。下面将介绍Excel图表中常见的一些元素及其作用,并附上相关截图。 原始数据 月份 网站访问量 (万次) 销售额 (万…...
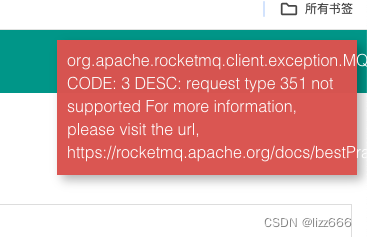
rocketmq dashboard控制台中topic状态无法展示
现象 在使用rocketmq控制台查看topic状态和订阅状态时,出现错误和没有信息的情况。 原因 rocketmq控制台版本问题,最新版本为1.0.1,支持rocketmq5版本,如果使用rocketmq4版本的服务无法兼容对应的数据。同理1.0.0版本也无法兼容ro…...

GPT每日面试题-Typescript中type和interface的区别
充分利用ChatGPT的优势,帮助我们快速准备前端面试。今日问题:typescript中type和interface的区别? Q:如果在前端面试中,被问到typescript的type和interface的区别是什么,怎么回答最好? A:当谈…...

python数据分析——大数据伦理风险分析
大数据伦理风险分析 前言一、大数据伦理二、大数据技术伦理风险2.1算法安全性、可信赖性及稳定性风险及其应对2.2算法的可解释性风险及其应对2.3算法的决策不可预见性风险及其应对2.4数据收集与储存中的泄漏风险及其应对2.5案例:某大型电商平台内部员工涉嫌窃取50亿…...
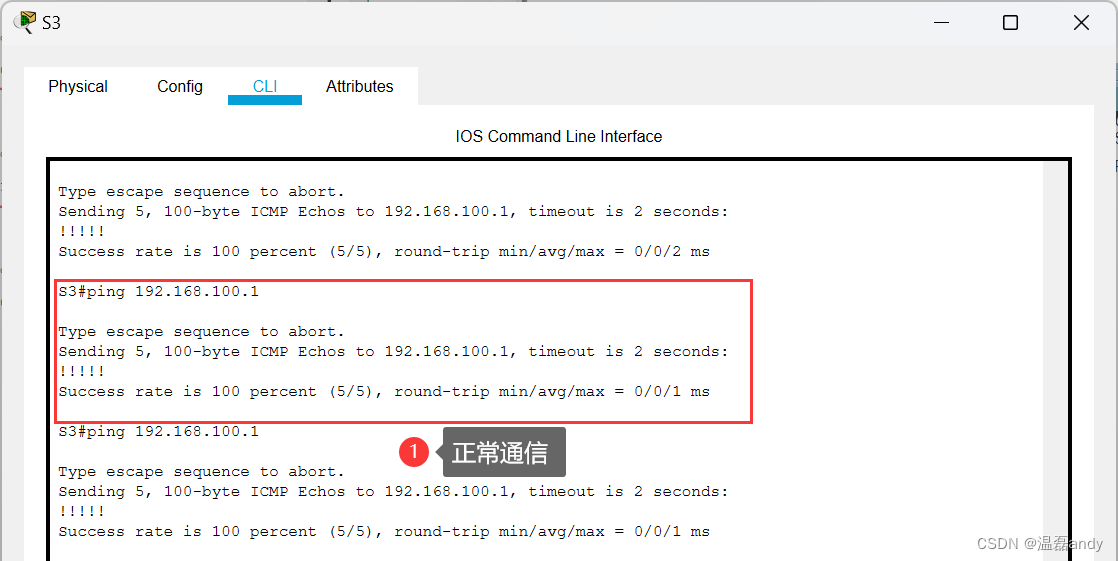
配置 Trunk,实现相同VLAN的跨交换机通信
1.实验环境 公司的员工人数已达到 100 人,其网络设备如图所示。现在的网络环境导致广播较多网速慢,并且也不安全。公司希望按照部门划分网络,并且能够保证一定的网络安全性。 其网络规划如下。 PC1和 PC3为财务部,属于VLAN 2&…...
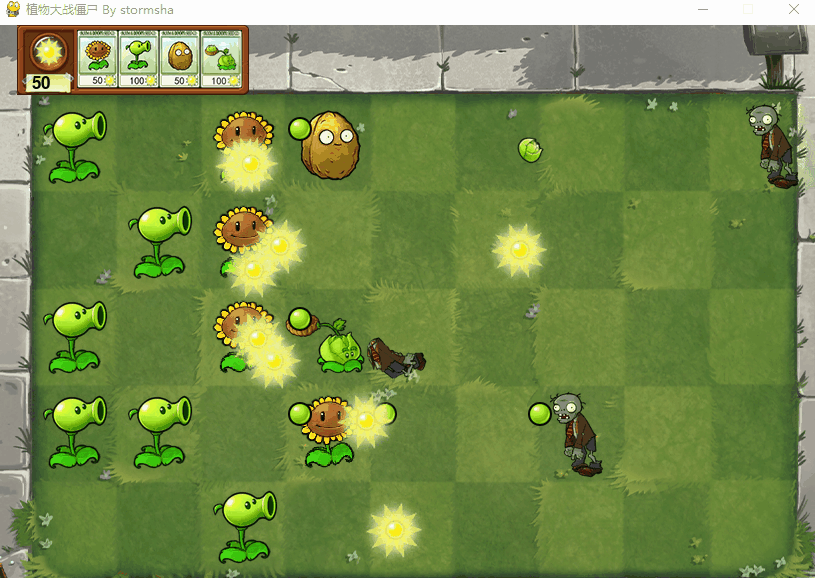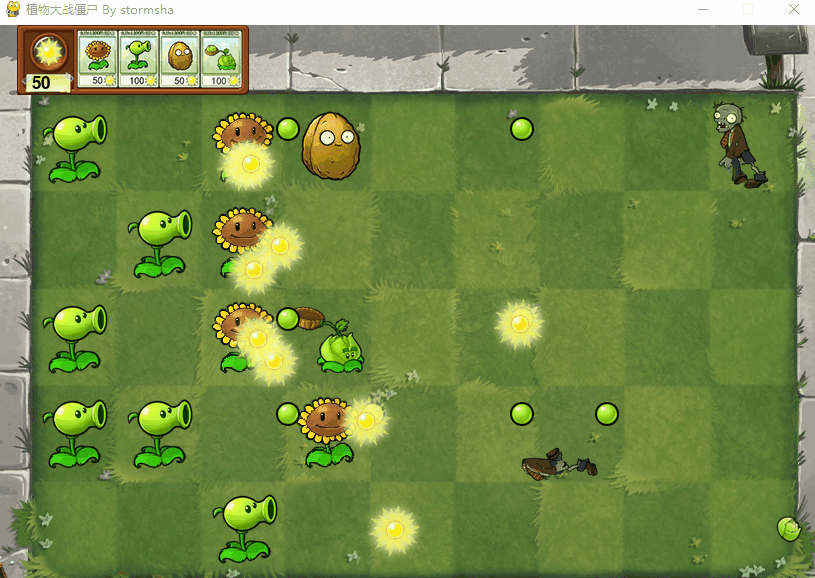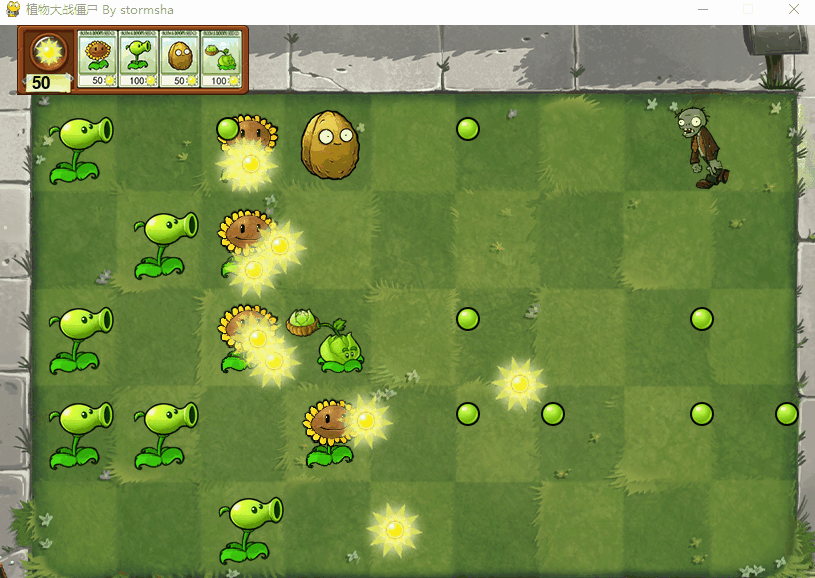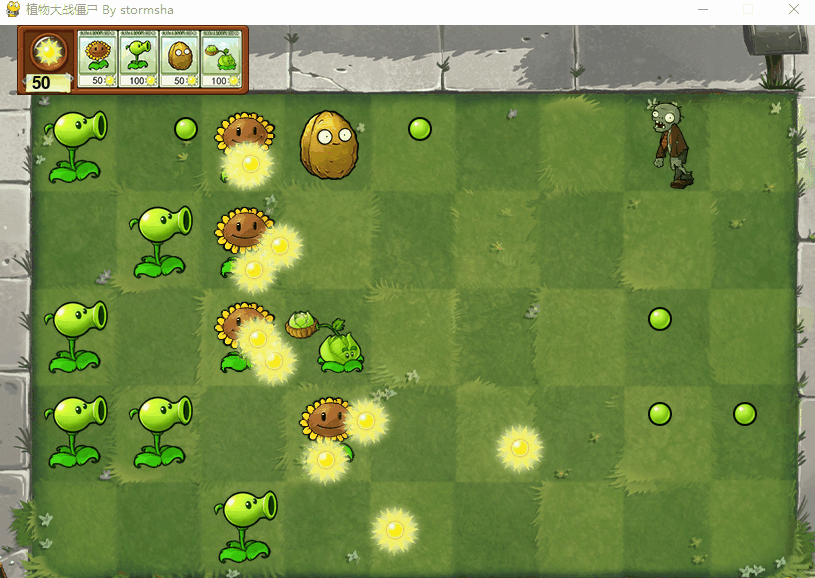
Python 植物大战僵尸
文章目录 效果图项目结构实现思路源代码 效果图 项目结构 实现思路 下面是代码的实现思路: 导入必要的库和模块:首先,我们导入了Python的os、time库以及pygame库,还有植物大战僵尸游戏中用到的各个植物和僵尸的类。 初始化游戏和…...

SpringBoot:实战项目TLIAS智能学习辅助系统1.1
SpringBootWeb项目 TILAS智能学习辅助系统 需求 部门管理 查询部门列表 删除部门 新增部门 修改部门 员工管理 查询员工列表(分页) 删除员工 新增员工 修改员工 准备工作 导入依赖 web(2.7.6) mybatis mysql驱动 lombok 准备好包结构 Controller->Servi…...

ubuntu-meta-22.04桌面版+ros2-humble 镜像
ubuntu-meta-22.04桌面版ros2-humble 镜像 下载地址: 链接:https://pan.baidu.com/s/1PSBe4EqWch44OQUlkCCEig?pwdknty 提取码:knty 镜像文件较大,分成了两个压缩包,下载后直接解压ubuntu22.04-desk-meta-ros2-arm (…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
