【双曲几何-05 庞加莱模型】庞加来上半平面模型的几何属性
文章目录
- 一、说明
- 二、双曲几何的上半平面模型
- 三、距离问题
- 四、弧长微分
- 五、面积问题
一、说明
庞加莱圆盘模型是表示双曲几何的一种方法,对于大多数用途来说它都非常适合几何作图。然而,另一种模型,称为上半平面模型,使一些计算变得更容易,包括三角形面积的计算。
二、双曲几何的上半平面模型
双曲几何的上半平面模型具有空间 U 由所有复数组成 z 这样我( z) > 0 , 和转化组 U 包括发送的所有莫比乌斯变换 U 对自己。空间 U 称为上半平面 C。
双曲几何的庞加莱圆盘模型可以通过由两次反演构建的莫比乌斯变换转移到上半平面模型,如下所示:
- 围绕圆反转 C 以i为圆心,经过 - 1 和 1 如图 5.5.1 。
- 对实轴对称。
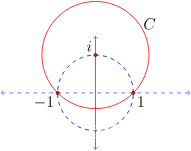
注意圆的反转C固定- 1和1,并且需要将i映射到无穷大。
由于穿过实轴的反射使这些图像点固定,因此两个反演的组合是莫比乌斯变换,它将单位圆带到实轴。该图还将圆盘的内部发送到上半平面。进一步注意莫比乌斯变换需要无穷大到-i;
因此,由定理3.5.1,map可以写成
V ( z ) = − i z + 1 z − i . . . . . . . . . . . . . . . . . . . . . . ( 5.5.1 ) V(z) = \dfrac{-iz + 1}{z - i}\text{.} ..................... (5.5.1) V(z)=z−i−iz+1......................(5.5.1)
这种莫比乌斯变换是将双曲平面的圆盘模型转移到上半平面模型的关键。事实上,当在这些模型之间来回切换时,本节采用以下约定是很方便的:让z表示其中的一个点d ,和w表示上半平面中的一个点U ,如图5.5.2。我们记录连接下面空间的转换。
在 (D,H) 之间移动 和(U,U)。莫比乌斯变换 V 映射D 给你, 及其逆 V − 1 V^{-1} V−1, 由下式给出:
w = V ( z ) = − i z + 1 z − i , 和 z = V 1 ( w ) = i w + 1 w + i . . . . . . . . ( 5.5.2 ) w=V(z)=\frac{−iz+1}{z−i }, 和 z=V_1(w)=\frac{iw+1}{w+i}........(5.5.2) w=V(z)=z−i−iz+1,和z=V1(w)=w+iiw+1........(5.5.2)
上半平面模型的一些特征立即显现出来。自从V是莫比乌斯变换,它保留斜线和角度。这意味着圆盘模型中的理想点,即无穷远圆上的点, S 1 S_1 S1无穷大,
已移动到实轴,并且圆盘模型中的双曲线已变为与实轴成直角相交的斜线。
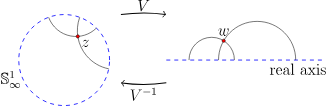
图-5.5. 2:将圆盘映射到上半平面。
三、距离问题
定义两点之间的双曲距离w1,w2在上半平面模型中,表示为 d U ( w 1 , w 2 ) d_U(w1,w2) dU(w1,w2),是圆盘模型中它们的原像之间的双曲距离。
认为w1和w2有两点在V其单位圆盘中的原像为z1和z2,分别。然后,
d U ( w 1 , w 2 ) = d H ( z 1 , z 2 ) = l n ( ( z 1 , z 2 ; u , v ) ) . . . . . . . . . . ( 5.5.3 ) d_U(w1,w2)=d_H(z1,z2)=ln((z1,z2;u,v)).......... (5.5.3) dU(w1,w2)=dH(z1,z2)=ln((z1,z2;u,v))..........(5.5.3)
在这里u和v是双曲线的理想点z1和z2。但是,由于交叉比在莫比乌斯变换下得以保留,
d U ( w 1 , w 2 ) = l n ( ( w 1 , w 2 ; p , q ) ) . . . . . . . . . . . . ( 5.5.4 ) d_U(w1,w2) = ln((w1,w2; p,q))............(5.5.4) dU(w1,w2)=ln((w1,w2;p,q))............(5.5.4)
在这里,是上半平面中双曲线的理想点w1和w2。特别是,从w1到w2我们正在走向理想点p 。
例子5.5. 1: 虚轴上点之间的距离ri和si。因为r > s > 0我们计算之间的距离我和我在上半平面模型中。
双曲线通过ri和si是正虚轴,有理想点0和无穷大。因此,
d U ( r i , s i ) = ln ( ( r i , s i ; 0 , ∞ ) ) = r i − 0 r i − ∞ ⋅ s i − ∞ s i − 0 = ln ( r s ) . \begin{align*} d_U(ri, si) & = \ln((ri, si; 0, \infty))\\ & = \dfrac{ri - 0}{ri - \infty}\cdot\dfrac{si-\infty}{si-0}\\ & = \ln\left(\dfrac{r}{s}\right)\text{.} \end{align*} dU(ri,si)=ln((ri,si;0,∞))=ri−∞ri−0⋅si−0si−∞=ln(sr).
例子5.5.2 :任意两点之间的距离。
求任意两点之间的距离 w1 和w2 在 U \mathbb{U} U 中, 我们首先在上半平面模型中构建一个映射,将这两个点移动到正虚轴。为了构建这张图,我们使用庞加莱圆盘模型。
通过改造 V 1 V_1 V1我们发送w1和w2回到 D \mathbb{D} D .我们让 z 1 = V 1 ( w 1 ) z_1=V_1(w1) z1=V1(w1)
和 z 2 = V 1 ( w 2 ) z_2=V_1(w_2) z2=V1(w2)。然后,让 S ( z ) = e i θ z − z 1 1 − z 1 ˉ z S(z)=e^{iθ}\frac{z−z1}{1−\bar{z_1}z} S(z)=eiθ1−z1ˉzz−z1
是转变 ( D 、 H ) (\mathbb{D}、\mathcal{H}) (D、H)发送z1到0和θ仔细选择,以便 z 2 z_2 z2被发送到正虚轴。实际上,z2被发送到ki,在这里 k = ∣ S ( z 2 ) ∣ = ∣ S ( V − 1 ( w 2 ) ) ∣ k = | S(z_2) | = | S(V^{- 1}(w_2) ) | k=∣S(z2)∣=∣S(V−1(w2))∣(和0 < k < 1)。然后,申请V就情况而言,0被发送到i,和ki被发送到 1 + k 1 − k i \frac{1 + k}{1 − k}i 1−k1+ki我。因此, V ∘ S ∘ V − 1 V∘ S∘V^{- 1} V∘S∘V−1发送w1到i;和w2
到 1 + k 1 − k i \frac{1 + k}{1 − k}i 1−k1+ki,其中通过前面的示例,点之间的距离是已知的:
d U ( w 1 , w 2 ) = l n ( 1 + k ) − l n ( 1 − k ) . . . . . . . . . . . . . ( 5.5.5 ) dU(w1,w2) = ln( 1 + k ) − ln( 1 − k ) .............(5.5.5) dU(w1,w2)=ln(1+k)−ln(1−k).............(5.5.5)
描述k按照w1和w2留给有冒险精神的读者。我们不需要在这里追究这个问题。
四、弧长微分
现在,我们再次通过圆盘模型导出上半平面模型的双曲弧长微分。回想一下圆盘模型中的弧长微分是
d s = 2 ∣ d z ∣ 1 − ∣ z ∣ 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 5.5.6 ) ds = \dfrac{2|dz|}{1-|z|^2}\text{.}..............................(5.5.6) ds=1−∣z∣22∣dz∣...............................(5.5.6)
自从 z = V − 1 ( w ) = i w + 1 w + i z = V^{-1}(w) = \dfrac{iw+1}{w+i} z=V−1(w)=w+iiw+1 我们可以计算出弧长微分dw。
我们需要对复杂表达式求导,这可以像实值表达式一样进行。开始了:
d s = 2 ∣ d z ∣ 1 − ∣ z ∣ 2 = 2 ∣ d ( i w + 1 w + i ) ∣ 1 − ∣ i w + 1 w + i ∣ 2 = 2 ∣ i ( w + i ) d w − ( i w + 1 ) d w ∣ ∣ w + i ∣ 2 / [ 1 − ∣ i w + 1 ∣ 2 ∣ w + i ∣ 2 ] = 4 ∣ d w ∣ ∣ w + i ∣ 2 − ∣ i w + 1 ∣ 2 = 4 ∣ d w ∣ ( w + i ) ( w ‾ − i ) − ( i w + 1 ) ( − i w ‾ + 1 ) = 4 ∣ d w ∣ 2 i ( w ‾ − w ) = ∣ d w ∣ I m ( w ) . \begin{align*} ds & = \dfrac{2|dz|}{1-|z|^2}\\ & =\dfrac{2|d\bigg(\dfrac{iw+1}{w+i}\bigg)|}{1-\bigg|\dfrac{iw+1}{w+i} \bigg|^2} \tag{$z = \dfrac{iw+1}{w+i}$}\\ & =\dfrac{2|i(w+i)dw-(iw+1)dw|}{|w+i|^2}\bigg/\bigg[1-\dfrac{|iw+1|^2}{|w+i|^2}\bigg]\tag{chain rule}\\ & = \dfrac{4|dw|}{|w+i|^2-|iw+1|^2}\\ & = \dfrac{4|dw|}{(w+i)(\overline{w}-i)-(iw+1)(-i\overline{w}+1)}\\ & = \dfrac{4|dw|}{2i(\overline{w}-w)}\\ & = \dfrac{|dw|}{{ Im}(w)}\text{.} \end{align*} ds=1−∣z∣22∣dz∣=1− w+iiw+1 22∣d(w+iiw+1)∣=∣w+i∣22∣i(w+i)dw−(iw+1)dw∣/[1−∣w+i∣2∣iw+1∣2]=∣w+i∣2−∣iw+1∣24∣dw∣=(w+i)(w−i)−(iw+1)(−iw+1)4∣dw∣=2i(w−w)4∣dw∣=Im(w)∣dw∣.(z=w+iiw+1)(chain rule)
这使我们得出以下定义:
定义:平滑曲线的长度平滑曲线的长度 r ( t ) r ( t ) r(t)为了 a ≤ t ≤ b a≤t≤b a≤t≤b在上半平面模型中 ( U , U ) , (\mathbb{U},{\cal U})\text{,} (U,U),
表示 L ( r ) , {\cal L}(\boldsymbol{r})\text{,} L(r), 是(谁)给的
L ( r ) = ∫ a b ∣ r ′ ( t ) ∣ Im ( r ( t ) ) d t . . . . . . . . . ( 5.5.7 ) {\cal L}(\boldsymbol{r}) = \int_a^b \dfrac{|\boldsymbol{r}^\prime(t)|}{\text{Im}(\boldsymbol{r}(t))}~dt\text{.}........(5.5.7) L(r)=∫abIm(r(t))∣r′(t)∣ dt.........(5.5.7)
例子5.5.3:曲线的长度。
求水平曲线的长度 r ( t ) = t + k i r ( t ) = t + k i r(t)=t+ki设定了 a ≤ t ≤ b a≤t≤b a≤t≤b ,注意 r ′ ( t ) = 1 r^′( t ) = 1 r′(t)=1
和 I m ( r ( t ) ) = k Im ( r ( t ) ) = k Im(r(t))=k 。因此,
L ( r ) = ∫ a b 1 k d t = b − a k . . . . . . . . . . . . . . . . . . . ( 5.5.8 ) {\cal L}(\boldsymbol{r}) = \int_a^b \dfrac{1}{k}~dt = \dfrac{b-a}{k}\text{.}..................(5.5.8) L(r)=∫abk1 dt=kb−a...................(5.5.8)
五、面积问题
由弧长微分 d s = d w Im ( w ) ds = \dfrac{dw}{\text{Im}(w)} ds=Im(w)dw 面积微分来了:
定义:区域面积
上半平面模型中 ( U , H ) (\mathbb{U} ,\mathcal{H}) (U,H)双曲几何中,一个区域的面积R 用笛卡尔坐标描述,表示为一个 A ( R ) A(R ) A(R),给的
A ( R ) = ∬ R 1 1 y 2 d x d y . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 5.5.9 ) A (R )=∬_ {R_1}\frac{1}{y^2} dxdy ............................(5.5.9) A(R)=∬R1y21dxdy............................(5.5.9)
例子5.5.4:求一个2/3-理想的三角形 的面积。
认为 w ∈ U w ∈ U w∈U位于单位圆上,并考虑2/3-理想三角形的区域1w∞,就是下图蓝线包围的区域,如图所示。
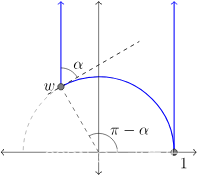
特别地,假设内角为w是α ,以便 w = e i ( π − α ) w =e^{i( π- α )} w=ei(π−α)在里这0 < α < π。
这个面积2/3- 理想三角形是这样的面积:
A = ∫ cos ( π − α ) 1 ∫ 1 − x 2 ∞ 1 y 2 d y d x = ∫ cos ( π − α ) 1 1 1 − x 2 d x . \begin{align*} A & = \int_{\cos(\pi - \alpha)}^1 \int_{\sqrt{1-x^2}}^\infty \dfrac{1}{y^2}~dydx\\ & = \int_{\cos(\pi - \alpha)}^1 \dfrac{1}{\sqrt{1-x^2}}~dx\text{.} \end{align*} A=∫cos(π−α)1∫1−x2∞y21 dydx=∫cos(π−α)11−x21 dx.
用三角函数替换 cos ( θ ) = x , \cos(\theta) = x\text{,} cos(θ)=x,,以便, 1 − x 2 = sin ( θ ) \sqrt{1-x^2} = \sin(\theta) 1−x2=sin(θ)因此有: − sin ( θ ) d θ = d x , -\sin(\theta)d\theta = dx\text{,} −sin(θ)dθ=dx,
积分变为:
= ∫ π − α 0 − sin ( θ ) sin ( θ ) d θ = π − α . \begin{align*} & =\int_{\pi - \alpha}^0\dfrac{-\sin(\theta)}{\sin(\theta)}~d\theta\\ & = \pi - \alpha\text{.} \end{align*} =∫π−α0sin(θ)−sin(θ) dθ=π−α.
事实证明,任何2/3- 理想三角形与其中一种形式全等1w∞,在这里w,位于单位圆的上半部分,并且由于我们的变换保留了角度和面积,因此我们已经证明了面积公式2/3-理想三角形。
定理5.5.1的面积为2/3-具有内角的理想三角形α,面积等于π- α 。
相关文章:

【双曲几何-05 庞加莱模型】庞加来上半平面模型的几何属性
文章目录 一、说明二、双曲几何的上半平面模型三、距离问题四、弧长微分五、面积问题 一、说明 庞加莱圆盘模型是表示双曲几何的一种方法,对于大多数用途来说它都非常适合几何作图。然而,另一种模型,称为上半平面模型,使一些计算变…...

Bookends for Mac:文献管理工具
Bookends for Mac,一款专为学术、研究和写作领域设计的文献管理工具,以其强大而高效的功能深受用户喜爱。这款软件支持多种文件格式,如PDF、DOC、RTF等,能够自动提取文献的关键信息,如作者、标题、出版社等,…...

SpringEL表达式编译模式SpelCompilerMode详解
目前网上没有搜到关于SpringEL表达式编译模式SpelCompilerMode的详细讲解,都是对官方文档的翻译,并没有详细说明根本差异。 该文章为个人原创,谢绝抄袭 SpringEL表达式官方文档:https://docs.spring.io/spring-framework/reference/core/expressions.html 在构建SpringE…...
物联网实战--平台篇之(一)架构设计
本项目的交流QQ群:701889554 物联网实战--入门篇https://blog.csdn.net/ypp240124016/category_12609773.html 物联网实战--驱动篇https://blog.csdn.net/ypp240124016/category_12631333.html 一、平台简介 物联网平台这个概念比较宽,大致可以分为两大类&#x…...

spi 驱动-数据发送流程分析
总结 核心函数是spi_sync, 设备驱动->核心函数-> 控制器驱动 实例分析 (gdb) c Continuing.Thread 115 hit Breakpoint 1, bcm2835_spi_transfer_one (master0xffffffc07b8e6000, spi0xffffffc07b911800, tfr0xffffff8009f53c40) at drivers/spi/spi-bcm2835…...
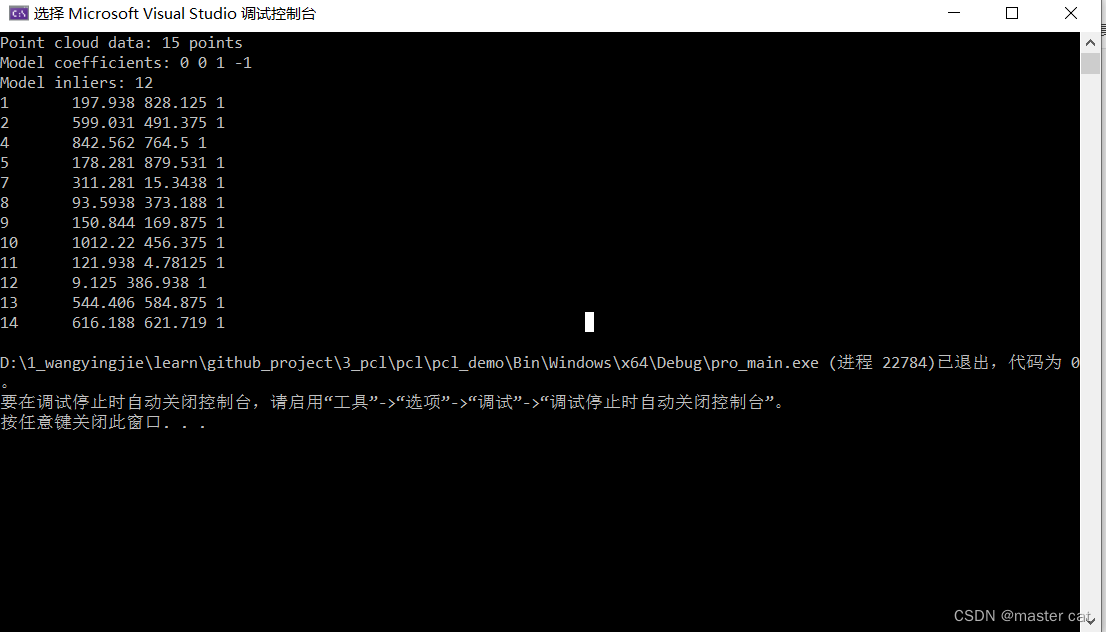
平面分割--------PCL
平面分割 bool PclTool::planeSegmentation(pcl::PointCloud<pcl::PointXYZ>::Ptr cloud, pcl::ModelCoefficients::Ptr coefficients, pcl::PointIndices::Ptr inliers) {std::cout << "Point cloud data: " << cloud->points.size() <<…...
前端之深拷贝
前提: 就是在实际开发中,我有一个编辑的弹窗,可以查看和编辑,因为弹窗里面是一个步骤条,点击下一步就要向对应的接口发送请求,考虑到就比如我点击下一步,此次表箱信息其实不需要修改࿰…...

2024年 Java 面试八股文——SpringCloud篇
目录 1.Spring Cloud Alibaba 中的 Nacos 是如何进行服务注册和发现的? 2.Spring Cloud Alibaba Sentinel 的流量控制规则有哪些? 3.Spring Cloud Alibaba 中如何实现分布式配置管理? 4.Spring Cloud Alibaba RocketMQ 的主要特点有哪些&…...

linux C语言Makefile
ChatGPT 在Linux中使用Makefile来自动化C语言项目的构建过程是很普遍的实践。Makefile是一个包含了一系列构建目标及如何构建这些目标的依赖和规则的文本文件。 一个基本的Makefile例子可能会像这样: # 定义编译器 CCgcc# 定义编译选项 CFLAGS-I.# 定义可执行文件…...
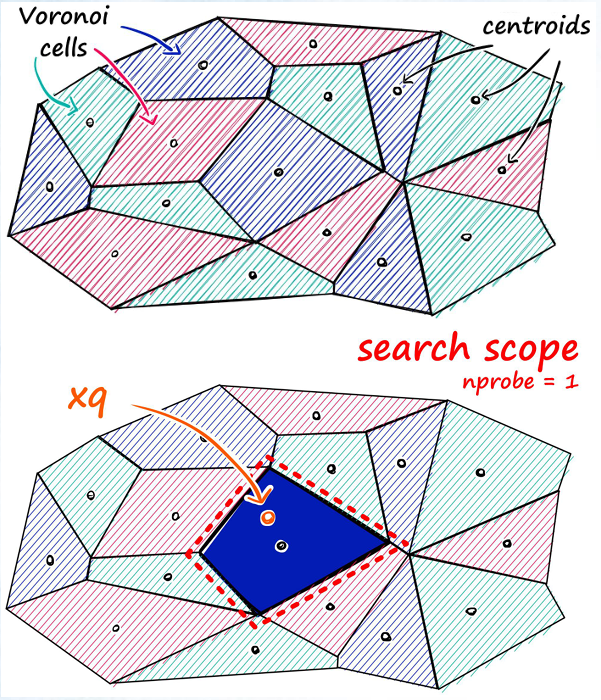
pgvector扩展在IvorySQL Oracle兼容模式下的应用实践
向量数据库是生成式人工智能(GenAI)的关键组成部分。作为PostgreSQL的重要扩展,pgvector支持高达16000维的向量计算能力,使得PostgreSQL能够直接转化为高效的向量数据库。 IvorySQL基于PostgreSQL开发,因此它同样支持添加pgvector扩展。在Ora…...

c++ 线程概述
C中的线程是并发编程的重要组成部分,它允许程序同时执行多个任务。以下是对C线程的概述: 基本概念: 并发:意味着两个或多个任务同时执行。在单核CPU上,由于只有一个CPU,某一时刻只能执行一个任务࿰…...

纯血鸿蒙APP实战开发——短视频切换实现案例
短视频切换实现案例 介绍 短视频切换在应用开发中是一种常见场景,上下滑动可以切换视频,十分方便。本模块基于Swiper组件和Video组件实现短视频切换功能。 效果图预览 使用说明 上下滑动可以切换视频。点击屏幕暂停视频,再次点击继续播放…...
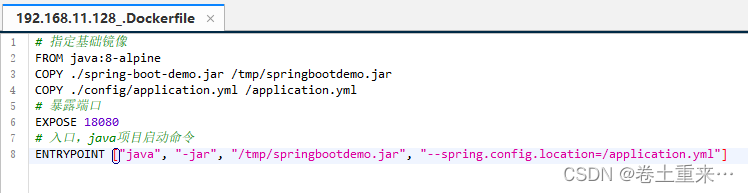
36.Docker-Dockerfile自定义镜像
镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而成。 镜像是分层机构,每一层都是一个layer BaseImage层:包含基本的系统函数库、环境变量、文件系统 EntryPoint:入口,是镜像中应用启动的命令 其他:在…...

【webrtc】MessageHandler 4: 基于线程的消息处理:以Fake 收发包模拟为例
G:\CDN\rtcCli\m98\src\media\base\fake_network_interface.h// Fake NetworkInterface that sends/receives RTP/RTCP packets.虚假的网络接口,用于模拟发送包、接收包单纯仅是处理一个ST_RTP包 消息的id就是ST_RTP 类型,– 然后给到目的地:mediachannel处理: 最后消息消…...

C#运算符“/”使用方法
C#中,当需要对两个整数进行除法运算时,结果会被截断为整数部分,即使结果本应是一个小数。这是因为整数除法会丢弃小数部分,只保留整数部分。 要想保留小数部分,需要将至少其中一个操作数转换为float、double或者 deci…...
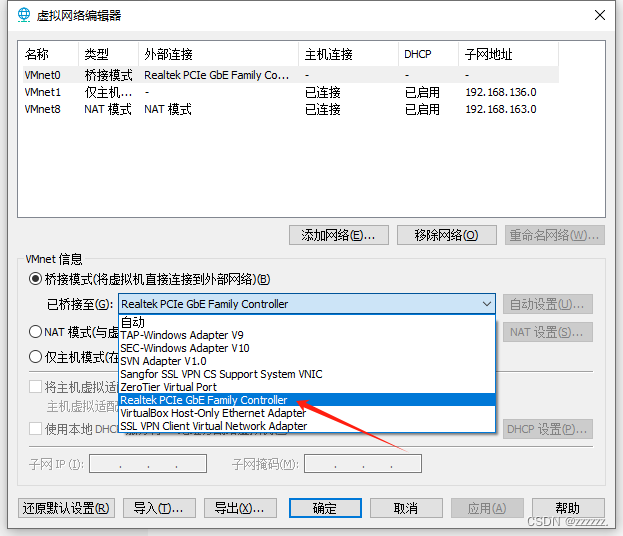
虚拟机网络桥接模式无法通信,获取到的ip为169.254.X.X
原因:VMware自动选择的网卡可能不对 解决:编辑-虚拟网络编辑器-更改桥接模式-选择宿主机物理网卡,断开虚拟机网络连接后重新连接即可...
【数据结构】初识数据结构
引入: 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我…...
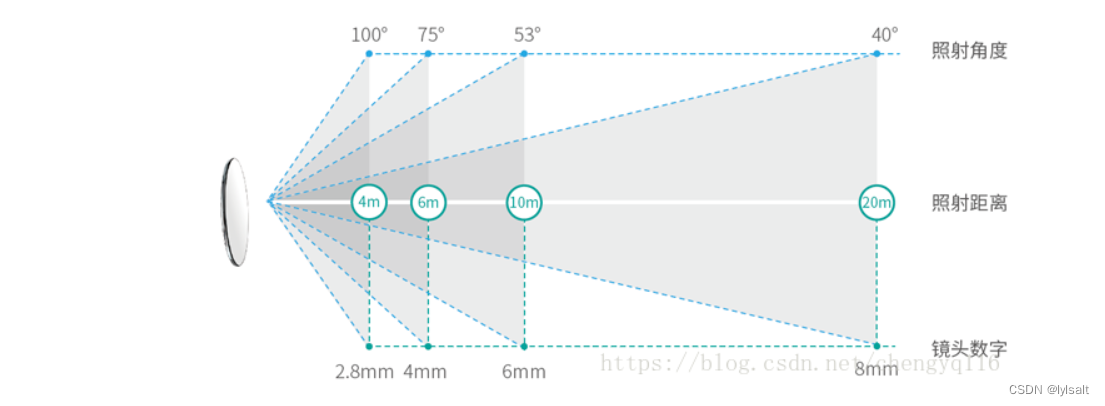
相机知识的补充
一:镜头 1.1MP的概念 相机中MP的意思是指百万像素。MP是mega pixel的缩写。mega意为一百万,mega pixel 指意为100万像素。“像素”是相机感光器件上的感光最小单位。就像是光学相机的感光胶片的银粒一样,记忆在数码相机的“胶片”ÿ…...

在Linux操作系统中实现磁盘开机自动挂载
当一个分区创建好,然后文件系统创建完毕之后, 需要使用mount命令将分区挂载到空目录上,这个挂载关系是临时的,也就是说当重启机器的时候,硬盘分区于空目录之间的挂载关系就会解除。 磁盘于目录之间的挂载关系断开意味…...

单片机编程实例400例大全(100-200)
今天继续分享单片机编程实例第100-200例。 今天的实例会比前面100复杂一些,我大概看了下,很多都具备实际产品的参考价值。 今天继续分享单片机编程实例第100-200例。 今天的实例会比前面100复杂一些,我大概看了下,很多都具备实际…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
