偏微分方程算法之混合边界条件下的差分法
目录
一、研究目标
二、理论推导
三、算例实现
四、结论
一、研究目标
我们在前几节中介绍了Poisson方程的边值问题,接下来对椭圆型偏微分方程的混合边值问题进行探讨,研究对象为:
其中,为矩形区域
,
为
上的连续函数,
是
上的单位法向量,从而
表示方向导数,
为
的连续函数且
非负。对于矩形区域
而言,其边界上的法向量没有统一的表达式,需要对四条边界线段分别讨论。可见:
在左边界,边界条件为
;
在右边界,边界条件为
;
在下边界,边界条件为
;
在上边界,边界条件为
。
于是,公式(1)可以具体写为:
二、理论推导
首先进行矩形区域的等距剖分,得到各网格节点
,且
,
;
,
。然后弱化原方程,使其仅在离散节点上成立,从而有
将上式中的一阶、二阶偏导数分别用关于一阶导数的中心差商和关于二阶导数的中心差商来近似,得
用数值解代替精确解并忽略高阶项,得到以下数值格式:
其中,。该格式的局部截断误差为
,同时需要处理其中的下标越界问题。由于函数的连续性,我们认为公式(2)中的第1式对i=0也成立,即有
再成公式(2)的第2式中解出代入上式,得
同样,设公式(2)中的第1式分别对成立,再分别从公式(2)的第3、4、5式中解出
代入前面刚得到的方程,就可以处理掉越界下标,得到以下格式:
至此我们共有(m+1)x(n+1)个待求量,而现有(m-1)x(n-1)个关于内节点的方程,2(n-1)个关于左、右边界上的节点(不含端点)的方程及2(m-1)个关于上、下边界上的节点(也不含端点)的方程,还需要补充
个方程,也就是关于矩形区域的4个顶点的方程。为此,设公式(2)中第1式对成立,即
然后再从公式(2)的第2式和第4式中分别解出和
,代入公式(3)中,得到
左下顶点处的方程:
上式可以简化为
同样,设公式(2)中第1式分别对、
和
成立,然后再从公式(2)中第3式和第4式解出
分别代入刚才得到的3个方程,就得到
的右下顶点、左上顶点、和右上顶点处的方程,这样,我们就有了完整的处理带导数边界条件的椭圆型方程的数值格式:
记,有
为计算分别,可将上述方程组写成矩阵形式。
首先,将公式(4)中第4、6、7式写成:
上面的式子可以简记为
其中,,
为m+1阶单位矩阵,且C为公式(5)最左端的三对角矩阵,
为公式(5)右端的向量,
。接着,公式(4)中的第1,2,3式可以写成
,
该式可以简记为
其中,为公式(6)中的三对角矩阵,
为公式(6)右端的向量。最后,公式(4)的第5、8、9式可以写成
该式可以简记为
其中,D为公式(7)中的三对角矩阵,为公式(7)右端的向量。于是,由公式(5)、(6)、(7)可得到公式(4)写成块三对角矩阵为
采用Gauss-Seidel迭代法求解公式(8)。
三、算例实现
用差分格式-公式(8)求解椭圆型方程混合边值问题:
已知精确解为。分别取步长为
和
,输出6个节点
和
处的数值解,并给出误差,要求在各节点处最大误差的迭代误差限为
。
代码如下:
#include <cmath>
#include <stdlib.h>
#include <stdio.h>
#define pi 3.14159265359int main(int argc, char*argv[])
{int m,n,i,j,k;double xa,xb,ya,yb,dx,dy,alpha,beta,gamma,maxerr;double *x,*y,**u,**v,**lambda,*d,kexi,eta,temp;double f(double x, double y);double lambda_function(double x, double y);double phi1(double y);double phi2(double y);double psi1(double x);double psi2(double x);double exact(double x, double y);xa=0.0;xb=2.0;ya=0.0;yb=1.0;m=64;n=32;printf("m=%d,n=%d.\n",m,n);dx=(xb-xa)/m;dy=(yb-ya)/n;beta=1.0/(dx*dx);gamma=1.0/(dy*dy);alpha=2*(beta+gamma);kexi=2.0/dx;eta=2.0/dy;x=(double*)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=xa+i*dx;y=(double*)malloc(sizeof(double)*(n+1));for(j=0;j<=n;j++)y[j]=ya+j*dy;u=(double**)malloc(sizeof(double*)*(m+1));v=(double**)malloc(sizeof(double*)*(m+1));lambda=(double**)malloc(sizeof(double*)*(m+1));for(i=0;i<=m;i++){u[i]=(double*)malloc(sizeof(double)*(n+1));v[i]=(double*)malloc(sizeof(double)*(n+1));lambda[i]=(double*)malloc(sizeof(double)*(n+1));}for(i=0;i<=m;i++){for(j=0;j<=n;j++){u[i][j]=0.0;v[i][j]=0.0;lambda[i][j]=lambda_function(x[i],y[j]);}}d=(double*)malloc(sizeof(double)*(m+1));k=0;do{maxerr=0.0;for(i=0;i<=m;i++)d[i]=f(x[i],y[0])-eta*psi1(x[i]);d[0]=d[0]-kexi*phi1(y[0]);d[m]=d[m]+kexi*phi2(y[0]);v[0][0]=(d[0]+2*gamma*u[0][1]+2*beta*u[1][0])/(alpha+(kexi+eta)*lambda[0][0]);for(i=1;i<m;i++)v[i][0]=(d[i]+2*gamma*u[i][1]+beta*(v[i-1][0]+u[i+1][0]))/(alpha+eta*lambda[i][0]);v[m][0]=(d[m]+2*gamma*u[m][1]+2*beta*v[m-1][0])/(alpha+(kexi+eta)*lambda[m][0]);for(j=1;j<n;j++){for(i=0;i<=m;i++){d[i]=f(x[i],y[j]);}d[0]=d[0]-kexi*phi1(y[j]);d[m]=d[m]+kexi*phi2(y[j]);v[0][j]=(d[0]+gamma*(u[0][j+1]+v[0][j-1])+2*beta*u[1][j])/(alpha+kexi*lambda[0][j]);for(i=1;i<m;i++){v[i][j]=(d[i]+gamma*(v[i][j-1]+u[i][j+1])+beta*(v[i-1][j]+u[i+1][j]))/alpha;}v[m][j]=(d[m]+gamma*(v[m][j-1]+u[m][j+1])+2*beta*v[m-1][j])/(alpha+kexi*lambda[m][j]);}for(i=0;i<=m;i++)d[i]=f(x[i],y[n])+eta*psi2(x[i]);d[0]=d[0]-kexi*phi1(y[n]);d[m]=d[m]+kexi*phi2(y[n]);v[0][n]=(d[0]+2*gamma*v[0][n-1]+2*beta*u[1][n])/(alpha+(kexi+eta)*lambda[0][n]);for(i=1;i<m;i++)v[i][n]=(d[i]+2*gamma*v[i][n-1]+beta*(v[i-1][n]+u[i+1][n]))/(alpha+eta*lambda[i][n]);v[m][n]=(d[m]+2*gamma*v[m][n-1]+2*beta*v[m-1][n])/(alpha+(kexi+eta)*lambda[m][n]);for(i=0;i<=m;i++){for(j=0;j<=n;j++){temp=fabs(u[i][j]-v[i][j]);if(temp>maxerr)maxerr=temp;u[i][j]=v[i][j];}}k=k+1;}while((maxerr>0.5*1e-10)&&(k<=1e+8));printf("k=%d\n",k);k=m/4;for(i=k;i<m;i=i+k){printf("(%.2f,0.25), y=%f, err=%.4e.\n",x[i],u[i][n/4],fabs(exact(x[i],y[n/4])-u[i][n/4]));}k=m/4;for(i=k;i<m;i=i+k){printf("(%.2f,0.50), y=%f, err=%.4e.\n",x[i],u[i][n/2],fabs(exact(x[i],y[n/2])-u[i][n/2]));}for(i=0;i<=m;i++){free(u[i]);free(v[i]);free(lambda[i]);}free(u);free(v);free(lambda);free(x);free(y);free(d);return 0;
}double f(double x, double y)
{return (pi*pi-1)*exp(x)*sin(pi*y);
}
double lambda_function(double x, double y)
{return x*x+y*y;
}
double phi1(double y)
{return (1-y*y)*sin(pi*y);
}
double phi2(double y)
{return (5.0+y*y)*exp(2.0)*sin(pi*y);
}
double psi1(double x)
{return pi*exp(x);
}
double psi2(double x)
{return -pi*exp(x);
}
double exact(double x, double y)
{return exp(x)*sin(pi*y);
}当时,计算结果如下:
m=32,n=16.
k=4323
(0.50,0.25), y=1.152179, err=1.3643e-02.
(1.00,0.25), y=1.911016, err=1.1100e-02.
(1.50,0.25), y=3.162159, err=6.8738e-03.
(0.50,0.50), y=1.638607, err=1.0115e-02.
(1.00,0.50), y=2.711255, err=7.0265e-03.
(1.50,0.50), y=4.479936, err=1.7526e-03.当时,计算结果如下:
m=64,n=32.
k=16007
(0.50,0.25), y=1.162412, err=3.4097e-03.
(1.00,0.25), y=1.919341, err=2.7745e-03.
(1.50,0.25), y=3.167313, err=1.7193e-03.
(0.50,0.50), y=1.646193, err=2.5286e-03.
(1.00,0.50), y=2.716524, err=1.7575e-03.
(1.50,0.50), y=4.481249, err=4.3972e-04.四、结论
从计算结果可知,当步长减小为1/2时,误差减小为原来的1/4,可见该数值格式是二阶收敛的。
相关文章:
偏微分方程算法之混合边界条件下的差分法
目录 一、研究目标 二、理论推导 三、算例实现 四、结论 一、研究目标 我们在前几节中介绍了Poisson方程的边值问题,接下来对椭圆型偏微分方程的混合边值问题进行探讨,研究对象为: 其中,为矩形区域,为上的连续函数…...
apollo资料整理
Application X: Application X Apollo: Apollo 自动驾驶开放平台 Cyber RT API tutorial — Cyber RT Documents documentation Cyber RT API tutorial — Cyber RT Documents documentation GitHub - daohu527/dig-into-apollo: Apollo notes (Apollo学习笔记) - Apollo l…...

森林消防新利器:高扬程水泵的革新与应用/恒峰智慧科技
随着全球气候变化的加剧,森林火灾的频发已成为威胁生态安全的重要问题。在森林消防工作中,高效、快速的水源供给设备显得尤为重要。近年来,高扬程水泵的广泛应用,为森林消防工作带来了新的希望与突破。 一、高扬程水泵的技术优势 …...
Microsoft Universal Print 与 SAP 集成教程
引言 从 SAP 环境打印是许多客户的要求。例如数据列表打印、批量打印或标签打印。此类生产和批量打印方案通常使用专用硬件、驱动程序和打印解决方案来解决。 Microsoft Universal Print 是一种基于云的打印解决方案,它允许组织以集中化的方式管理打印机和打印机驱…...
VBA在Excel中字母、数字的相互转化
VBA在Excel中字母、数字的相互转化 字母转数字的方法 数字转字母的方法 众所周知,Excel表中的行以数字展示,列用字母展示,如下图: 编程时,很多时候需要将列的字母转变为数字使用,如cells(num1,num2).value等,不知大家是怎么将字母转化为数字的,Excel是否有其他方式…...

【C语言】——联合体与枚举
【C语言】——联合体与枚举 一、联合体1.1、联合体类型的声明1.2、联合体的特点1.3、相同成员的结构体和联合体对比1.4、联合体的大小计算1.5、联合体的应用举例 二、枚举2.1、枚举类型的声明2.2、枚举类型的优点 一、联合体 1.1、联合体类型的声明 联合体也叫做共用体 与…...
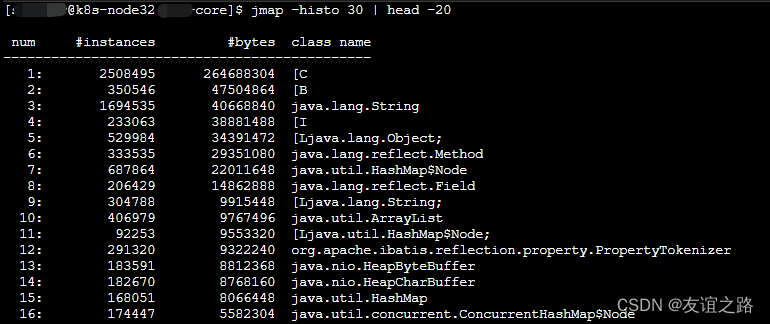
java线上问题排查之内存分析(三)
java线上问题排查之内存分析 使用top命令 top命令显示的结果列表中,会看到%MEM这一列,这里可以看到你的进程可能对内存的使用率特别高。以查看正在运行的进程和系统负载信息,包括cpu负载、内存使用、各个进程所占系统资源等。 2.用jstat命令…...

中电金信:金Gien乐道 | 4月要闻速览,精彩再回顾
中国电子党组副书记、总经理李立功一行调研中电金信 4月10日,中国电子党组副书记、总经理李立功一行赴中电金信进行调研,深入听取了中电金信经营发展情况、研发工作及“源启”行业数字底座平台的汇报,并参观了公司展厅和科技研发场所…...

Java将文件目录转成树结构
在实际开发中经常会遇到返回树形结构的场景,特别是在处理文件系统或者是文件管理系统中。下面就介绍一下怎么将文件路径转成需要的树形结构。 在Java中,将List<String>转换成树状结构,需要定义一个树节点类(TreeNode&#…...

硬件工程师必读:10条职业发展黄金法则!
在快速发展的科技时代,硬件工程师作为推动技术创新和产业升级的重要力量,其职业发展之路既充满挑战也蕴含无限机遇。为了在这条道路上稳步前行,我们首先需要了解硬件产品的研发流程。 在这个过程中,公司内的每个岗位都发挥着不可或…...
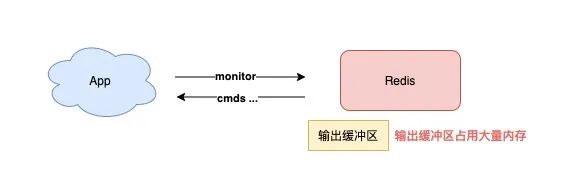
Redis是什么? 日常运维 Redis 需要注意什么 ? 怎么降低Redis 内存使用 节省内存?
你的项目或许已经使用 Redis 很长时间了,但在使用过程中,你可能还会或多或少地遇到以下问题: 我的 Redis 内存为什么增长这么快?为什么我的 Redis 操作延迟变大了?如何降低 Redis 故障发生的频率?日常运维…...
【Android项目】“追茶到底”项目介绍
没有多的介绍,这里只是展示我的项目效果,后面会给出具体的代码实现。 一、用户模块 1、注册(第一次登陆的话需要先注册账号) 2、登陆(具有记住最近登录用户功能) 二、点单模块 1、展示饮品列表 2、双向联动…...
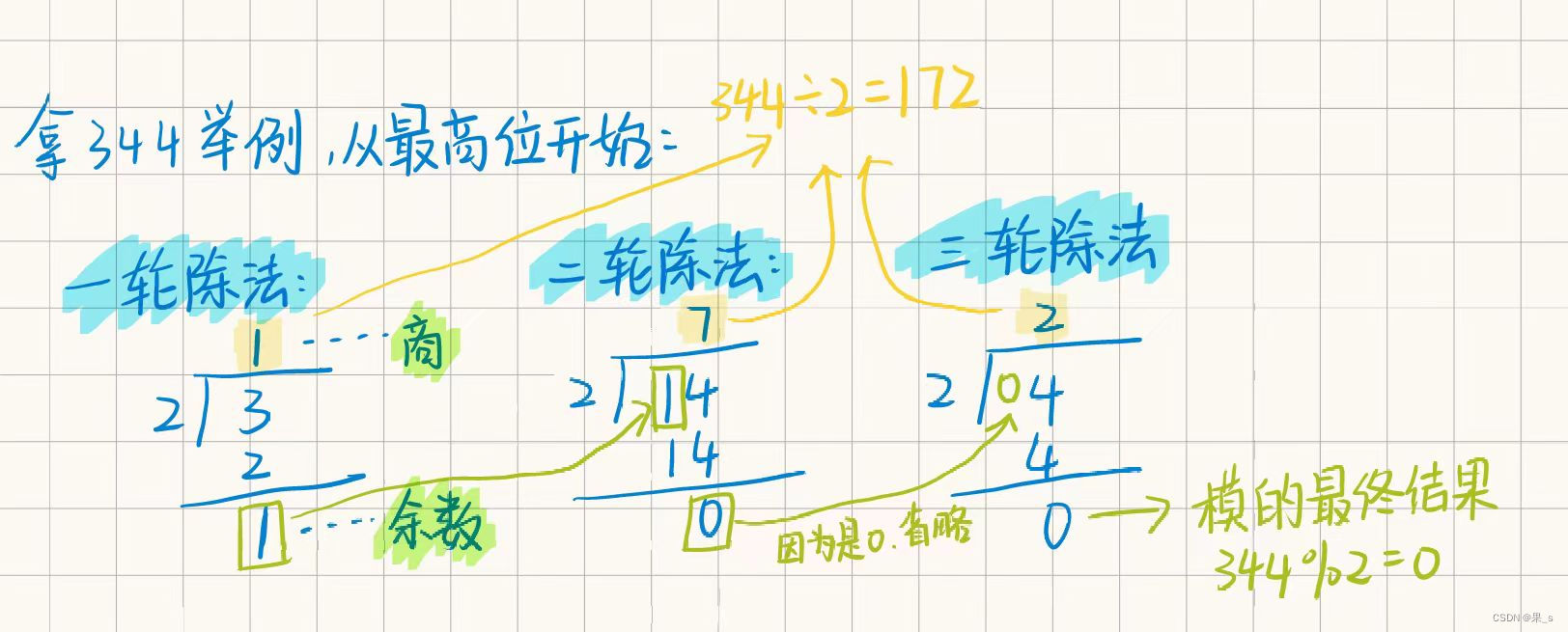
机试:进制转换问题
十进制转任意进制 简单回忆一下十进制我们是怎么转换成二进制的(短除法): 我们会将十进制数不断的进行除2操作,并且记录下每一次的余数(这个余数就是我们最终求的二进制数的组成部分)。 以下以12D举例&a…...

目标检测实战(十五): 使用YOLOv7完成对图像的目标检测任务(从数据准备到训练测试部署的完整流程)
文章目录 一、目标检测介绍二、YOLOv7介绍三、源码/论文获取四、环境搭建4.1 环境检测 五、数据集准备六、 模型训练七、模型验证八、模型测试九、错误总结9.1 错误1-numpy jas mp attribute int9.2 错误2-测试代码未能跑出检测框9.3 错误3- Command git tag returned non-zero…...

github中fasttext库README官文文档翻译
参考链接:fastText/python/README.md at main facebookresearch/fastText (github.com) fastText模块介绍 fastText 是一个用于高效学习单词表述和句子分类的库。在本文档中,我们将介绍如何在 python 中使用 fastText。 环境要求 fastText 可在现代 …...
WouoUIPagePC端实现
WouoUIPagePC端实现 WouoUIPage是一个与硬件平台无关,纯C语言的UI库(目前只能应用于128*64的单色OLED屏幕上,后期会改进,支持更多尺寸)。因此,我们可以在PC上实现它,本文就以在PC上使用 VScode…...

W801学习笔记十九:古诗学习应用——下
经过前两章的内容,背唐诗的功能基本可以使用了。然而,仅有一种模式未免显得过于单一。因此,在本章中对其进行扩展,增加几种不同的玩法,并且这几种玩法将采用完全不同的判断方式。 玩法一:三分钟限时挑战—…...
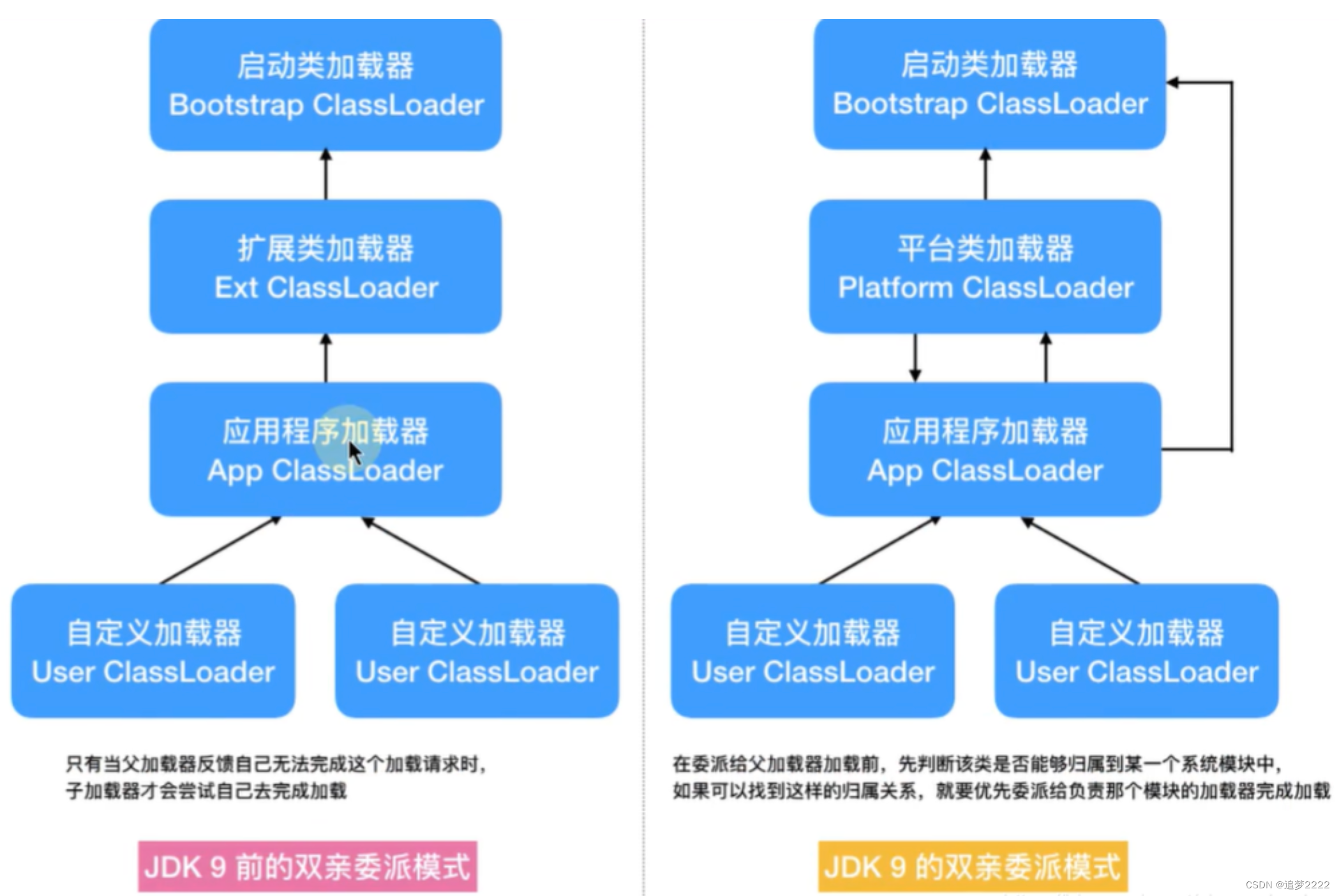
类加载器ClassLoad-jdk1.8
类加载器ClassLoad-jdk1.8 1. 类加载器的作用2. 类加载器的种类(JDK8)3. jvm内置类加载器如何搜索加载类--双亲委派模型4. 如何打破双亲委派模型--自定义类加载器5. 自定义一个类加载器5.1 为什么需要自定义类加载器5.2 自定义一个类加载器 6. java代码加…...
24年最新AI数字人简单混剪
24年最新AI数字人简单混剪 网盘自动获取 链接:https://pan.baidu.com/s/1lpzKPim76qettahxvxtjaQ?pwd0b8x 提取码:0b8x...

免备案香港主机会影响网站收录?
免备案香港主机会影响网站收录?前几天遇到一个做电子商务的朋友说到这个使用免备案香港主机的完整会不会影响网站的收录问题,这个问题也是站长关注较多的问题之一。小编查阅了百度官方规则说明,应该属于比较全面的。下面小编给大家介绍一下使用免备案香…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
