【初阶数据结构】单链表之环形链表
目录标题
- 前言
- 环形链表的约瑟夫问题
- 环形链表
- 环形链表||

前言
前面我们已经学习了关于单链表的一些基本东西,今天我们来学习单链表的一个拓展——环形链表,我们将用力扣和牛客网上的三道题目来分析讲解环形链表问题。
环形链表的约瑟夫问题
我们首先来看一道非常经典的题目——环形链表的约瑟夫问题。题目问题如下:
输入:5,2
输出:3
说明:
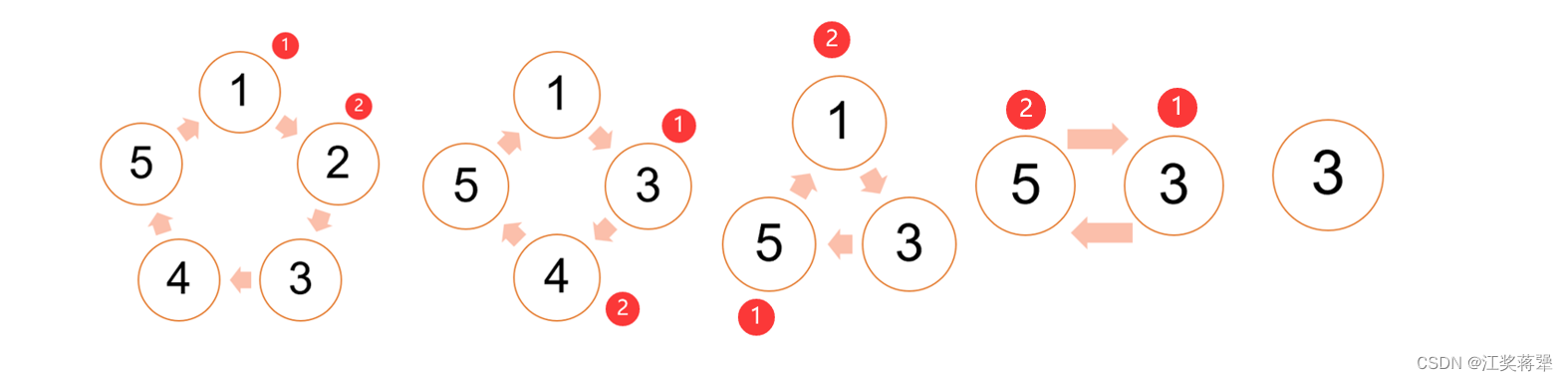
开始5个人 1,2,3,4,5 ,从1开始报数,1->1,2->2编号为2的人离开
1,3,4,5,从3开始报数,3->1,4->2编号为4的人离开
1,3,5,从5开始报数,5->1,1->2编号为1的人离开
3,5,从3开始报数,3->1,5->2编号为5的人离开
最后留下人的编号是3
看着问题好像无从下手,但只要掌握了链表的相关知识,你也能拿捏环形链表题目。
这道题目说将n个人围城一个圈,转换成链表也就是将n个节点串起来变成一个圈,即将最后一个节点的next指针指向头节点,这样环形链表就出现了。
当有5个人,编号为2的离开,流程如下
代码实现(解析包含在代码中)
/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param n int整型 * @param m int整型 * @return int整型*///题目中没有给出链表,我们首先要自己创建一个链表typedef struct ListNode ListNode;//给节点重命名ListNode* buyNode(int x)//建立新节点{ListNode* node = (ListNode*)malloc(sizeof(ListNode));if(node == NULL){exit (1);}node->val = x;node->next = NULL;return node;}ListNode* createCircle(int n){ListNode* phead = buyNode(1);//首先创建头节点,使后面的节点都能相连ListNode* ptail = phead;for(int i = 2;i <= n;i++){ptail->next = buyNode(i);ptail = ptail->next;}ptail->next = phead;//尾节点的next指向头节点,使其成为环形链表return ptail;//返回尾节点}
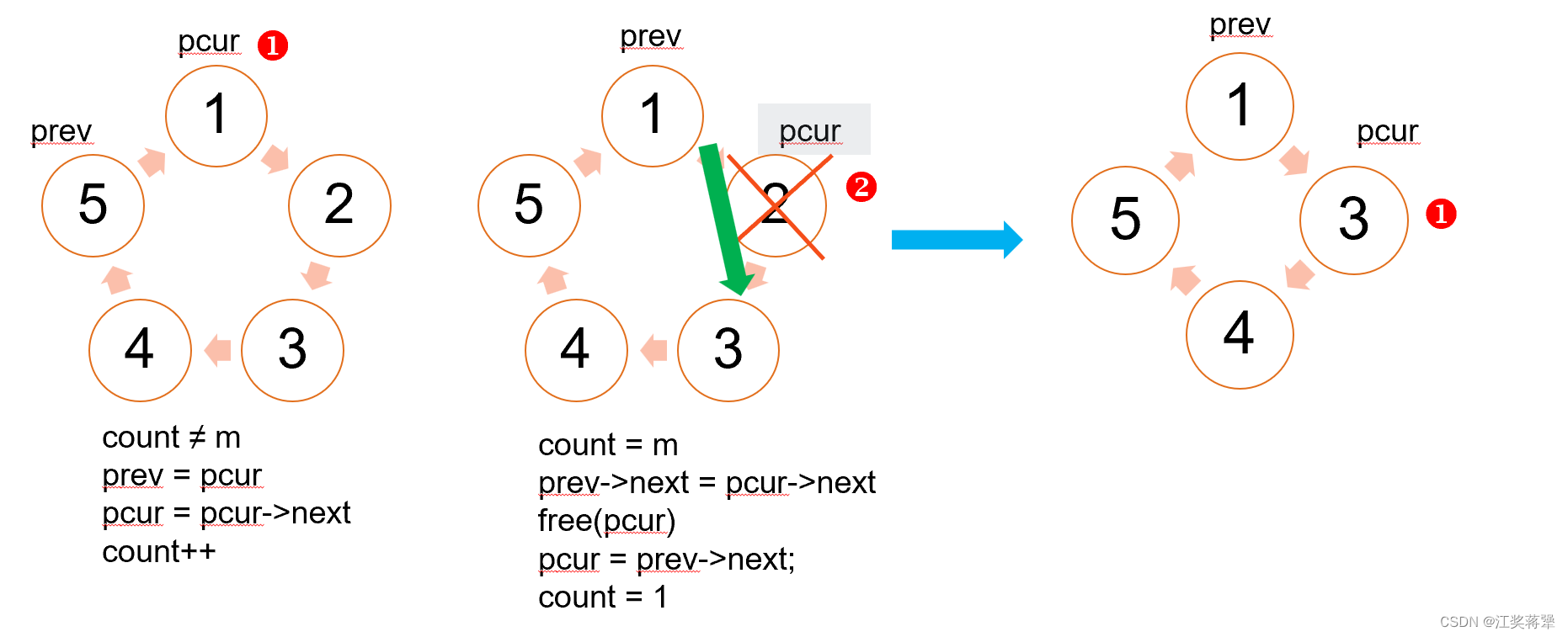
int ysf(int n, int m ) {// write code hereListNode* prev = createCircle(n);ListNode* pcur = prev->next;//让尾节点的下一个节点也就是头节点赋给pcur,让其成为数数的起始点。int count = 1;//开始第一次数数记为1while(pcur->next != pcur)//结束的标志是pcur->next == pcur,此时就只剩pcur这一个节点,则跳出循环{if(count == m)//如果pcur所对应的这个节点的值恰好为m,则要删除这个节点,在单链表中我们也讲过删除节点要怎么删除,便不再多讲{prev->next = pcur->next;free(pcur);pcur = prev->next;count = 1;//pcur往下走了一个节点要记得把count置为1,继续下一次循环}else //不为m时,prev指针和pcur指针都往下走一个,且pcur对应的报数count要加加{prev = pcur;pcur = pcur->next;count ++;}}return pcur->val;
}
环形链表
学会的环形链表的约瑟夫问题,下面来两道力扣中的环形链表问题
题目链接如下:环形链表。题目如下:
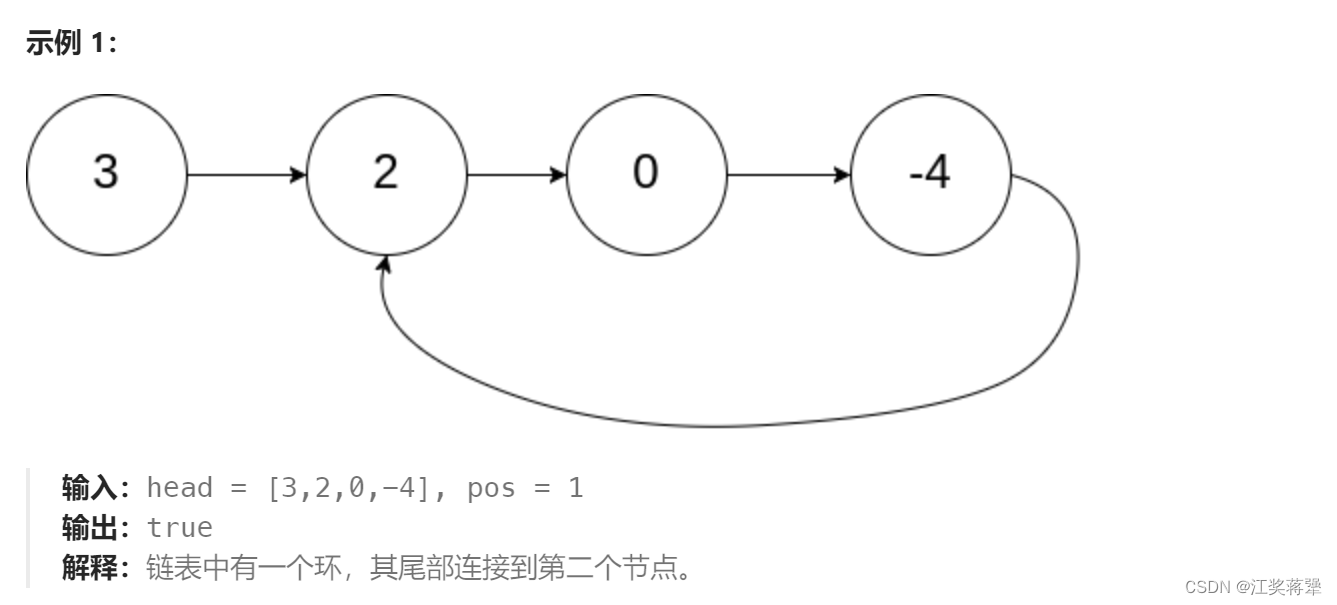
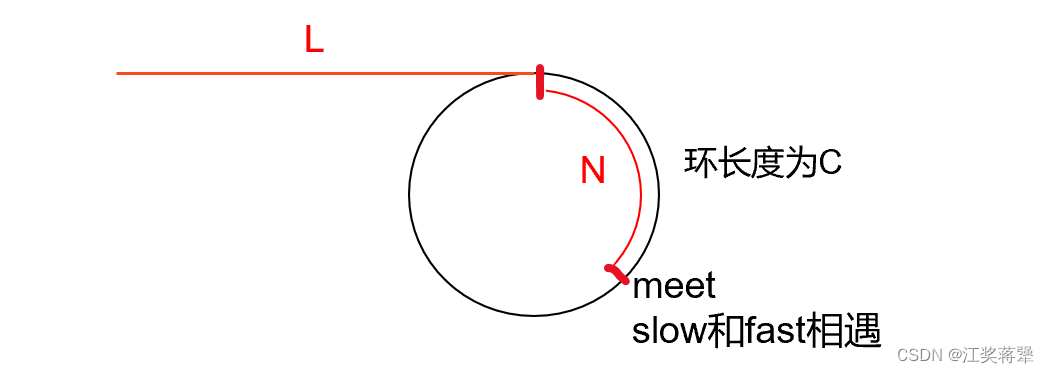
我们要判断一个链表看其是否有环,先说结论,我们可以利用快慢指针进行求解。顾名思义,快慢指针就是存在两个指针,一个走的快,一个走的慢,快指针一次走走两步或三步四步都可以,慢指针一般走一步。
这道题中,我们让快指针一次性走两边,慢指针一次性走一步,当慢指针进入环以后,快指针开始追慢指针,如果快指针能追上慢指针,也就是两指针相遇,则证明该链表带环。 代码如下:
/**1. Definition for singly-linked list.2. struct ListNode {3. int val;4. struct ListNode *next;5. };*/
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {ListNode* slownode = head, *quicknode = head;//定义快慢指针while(quicknode && quicknode->next)//快指针以及快指针指向的下一个节点不为空,则一直循环{slownode = slownode->next;//慢指针一次走一步quicknode = quicknode->next->next;//快指针一次走两步if(quicknode == slownode)//快慢指针相遇,则链表带环{return true;}}return false;//为空跳出循环说明该链表不带环
}
下面将解决大家的疑惑点:
- 为什么快慢指针一定会相遇,而不是会错过,如何证明
- 当慢指针走一步,快指针走3步,4步……又一定能追上相遇吗,如何证明
这两个问题我们来一一解决。
首先是第一个问题:为什么快慢指针一定会相遇,而不是会错过,如何证明。我们可以将快慢指针走的过程图画出来
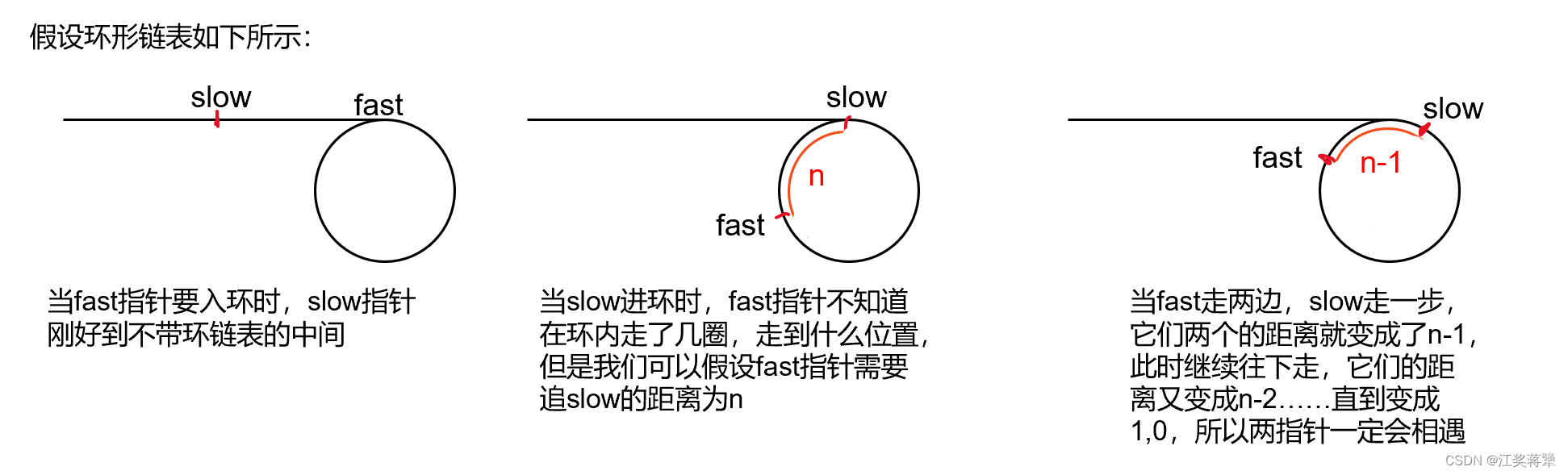
所以当快指针一次走两步,慢指针一次走一步时,如果链表带环,二者一定会在环内相遇,这就证明解决了第一个问题:
下面是第二个问题:当慢指针走一步,快指针走3步,4步……又一定能追上相遇吗,如何证明。
当慢指针一次走一步,快指针一次走3步时,证明如下:
当slow进环时,fast和slow的距离为n
slow一次走一步,fast一次走三步
则它们每追击一次,距离缩小2,
n是偶数 n是奇数 n n n-2 n-2 …… …… 4 3 2 1 0 -1 追上了 错过了,进行新一轮追击 如果n是奇数,fast错过了slow,此时fast到了slow前面一格,假设环的长度为C,则slow和fast是距离变为了C-1,开始新一轮追击,还是讨论C-1是偶数还是奇数的问题,如果C-1是偶数,就能追上,如果C-1是奇数,那永远不会追上。
根据以上分析我们可以得出结论:
- 当n时偶数,第一轮就能追上
- 当n时奇数时,第一轮追击会错过,二者的距离变成C-1(C是环的长度)
- 如果C-1是偶数,即C是奇数,那么下一轮就能追上相遇
- 如果C-1是奇数,即C是偶数,那么永远追不上
看似我们已经讨论出了有追上和追不上的这两种情况,但是追不上的情况:即n是奇数C是偶数的情况真的会存在吗,我们可以继续往下讨论:
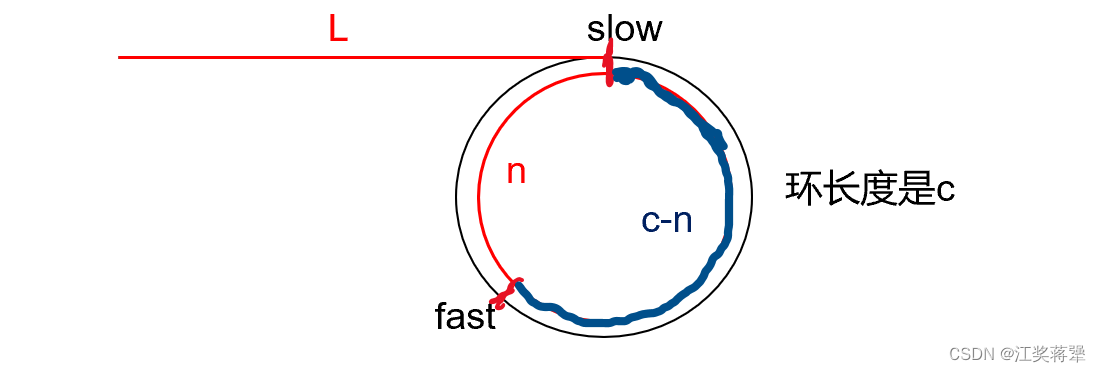
当slow进环时,fast和slow的距离为n
slow一次走一步,fast一次走三步
我们就能发现fast走的距离是slow的三倍
根据这个关系可以列出等式
slow走的距离:L
fast走的距离:L+x * c+c-n(slow进环时,假设fast已经在环里面转了n圈)
则得到等式:3 * L = L+x * c+c-n
化简得到:2 * L = (x+1) * c-n
2*L必定是偶数,
根据上面得出的结论:当n是奇数,c是偶数时,永远追不上
将其带入右边的式子,得到:(x+1)*偶数 - 奇数,此时得到的式子只能是奇数,与左边不等,则发现永远追不上的条件不成立。
根据以上一系列分析,可以得出结论:
当slow一次走一步,fast一次走三步时,若n是偶数,则第一轮就能追上,若n是奇数,c是奇数时,第二轮追上,即无论如何,一定能相遇追上。当fast一次走4步或者5步时也是同样的证明方法。
环形链表||
这道题的环形链表是上一道题的进阶,如果链表中有环,则要返回入环的第一个节点,没环则返回空,题目链接如下:环形链表||

对于本题,我们用到的是和上一题差不多一样的思路,首先判断有没有环,就用快慢指针,发现有环,要找到入环的第一个节点,我们有两种办法解决:
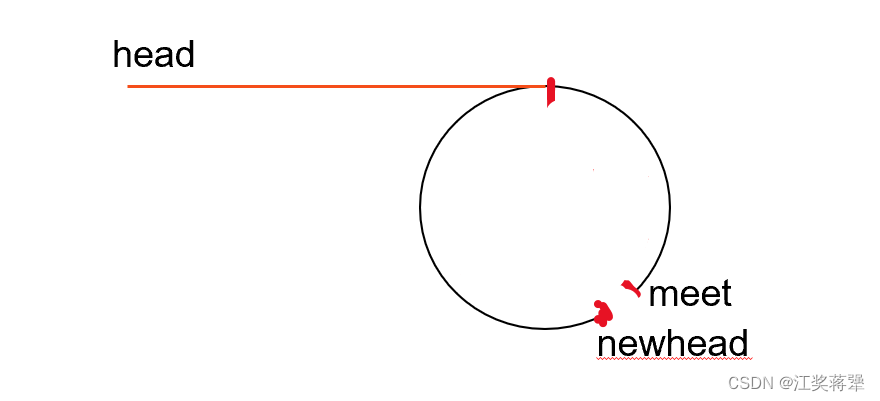
- 将快慢指针相遇时的节点我们记为meet节点,
然后让头节点和meet节点同时走,每次都走一步,当二者相遇时的节点就是进环时的第一个节点。 - 将快慢指针相遇时的节点我们记为meet节点,然后将meet节点与meet的下一个节点断开,使其形成两条链,此时就变成了求两条链表的相交问题(代码写起来较为复杂)
下面一一讲解:
对于方法一:
我们需要证明的是:为什么让头节点和meet节点一起每次走一步,当二者相遇的时候就是进环节点。
上一题我们通过画图找等式来解决为什么一定相遇,这题我们同样可以通过画图找等式解决。
我们用快慢指针,快指针一次走两步,慢指针一次走一步
则快指针走的路程是慢指针的两倍
由图,slow和fast相遇时距离进环时的一个节点为N:
slow走的距离:L+N (slow指针在环内走不到一整圈,因为当slow走一圈,fast在环内走两圈,肯定早就会相遇,所以slow指针在环内只能走N的距离)
fast走的距离:L+x * C +N (slow进环前,fast指针已经走了x圈)
所以得到等式:2 * (L+N) = L + x * C + N
化简得到:L = (x - 1)*C + C - N
(x - 1)*C是圈数
C - N 是meet节点与进环节点的距离,二者相加刚好为L
这就是为什么头结点和meet节点每次同时走一步,二者相遇时就是进环节点
代码如下:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {ListNode* fast = head, *slow = head;//给定两个快慢指针while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow)//相遇则带环{ListNode* phead = head;ListNode* meet = slow;//相遇节点置为meetwhile(phead != meet){phead = phead->next;meet = meet->next;//头节点和meet节点每次走一步}return phead;//相遇,返回其节点}}return NULL;//不带环返回空}
对于方法二:
我们要知道如何把环形链表断开,使其成为两条链表,并找到两条链表的相交节点,即为进环节点。
将meet的下一个节点记为newhead,并将其断开,此时就有head和newhead两条链,求这两条链表的相交节点即可。
代码如下:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {//定义一个函数,寻找两条链表的相交节点ListNode* l1 = headA, *l2 = headB;int a_count = 1, b_count = 1;while(l1->next){l1 = l1->next;a_count++;//给A链表长度计数}while(l2->next){l2 = l2->next;b_count++;//给B链表长度计数}//此时l1和l2都到达了两条链表的尾节点if(l1 != l2)//如果二者不相等,说明两条链表不想交{return NULL;}//到这,说明两条链表尾节点相等,链表相交int gap = abs(a_count - b_count);//得到两链表节点个数的差值ListNode* fastnode = headA, *slownode = headB;//假定长链表为链表A,短链表为链表Bif(b_count > a_count)//如果B链表节点数多则交换{fastnode = headB;slownode = headA;}//就能保证fastnode一定是长的那个链表while(gap){fastnode = fastnode->next;//先让长的链表走它们的差值gap--;}while(fastnode != slownode){fastnode = fastnode->next;slownode = slownode->next;//两链表一起走,相等了则为相交节点}return fastnode;
}
struct ListNode *detectCycle(struct ListNode *head) {ListNode* fast = head, *slow = head;while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow){ListNode* phead = head;ListNode* meet = slow;//相遇节点置为meetListNode* newhead = meet->next;//meet节点的下一节点作为新链表的头结点newheadmeet->next = NULL;//将其断开return getIntersectionNode(phead,newhead);//返回两条链表的相交节点。}}return NULL;}
方法二就到此结束,代码比较长是因为设计到了两条链表相加节点的问题,在力扣上也有此题目,大家也可以下去做做,链接如下:相交链表。
本篇内容到此结束了,关于链表大家要自己多想多画图多练习。感谢大家观看,如果大家喜欢,希望大家一键三连支持一下,如有表述不正确,也欢迎大家批评指正。

相关文章:

【初阶数据结构】单链表之环形链表
目录标题 前言环形链表的约瑟夫问题环形链表环形链表|| 前言 前面我们已经学习了关于单链表的一些基本东西,今天我们来学习单链表的一个拓展——环形链表,我们将用力扣和牛客网上的三道题目来分析讲解环形链表问题。 环形链表的约瑟夫问题 我们首先来看…...

【积分,微分,导数,偏导数公式推导】
1. 积分 积分是微积分的一个分支,用于计算曲边梯形的面积或者变速直线运动的总距离等。积分分为不定积分和定积分。 不定积分:给出一个函数,求出其所有可能的原函数。定积分:计算一个函数在特定区间上的积分。 2. 微分 微分是…...
java:递归实现的案例
//求第20个月兔子的对数 //每个月兔子对数:1,1,2,3,5,8 public class Test {//求第20个月兔子的对数//每个月兔子对数:1,1,2,3,5,8pu…...

Arxml文件解析03- 自动驾驶Radar服务radar_svc.arxml
<AR-PACKAGES><AR-PACKAGE><SHORT-NAME>bosch</SHORT-NAME><AR-PACKAGES>...</AR-PACKAGES>...

Elasticsearch安装步骤
引言 Elasticsearch是一个基于Lucene构建的开源、分布式、RESTful搜索和分析引擎。它设计用于云计算中,能够达到实时搜索,稳定,可靠,快速,安装使用方便。Elasticsearch为所有类型的数据提供近乎实时的搜索和分析。无论…...
Windows系统和unbtun系统连接usb 3.0海康可见MVS和红外艾睿相机
一.海康可见USB3.0工业面阵相机 海康usb相机需要去海康官网上下载对应系统的MVS客户端及SDK开发包 海康机器人-机器视觉-下载中心 选择Windows系统和unbtun(我是linux aarch64,所以选择了对应压缩包解压) Windows系统 1.双击安装包进入安装界面&…...

深入Django:用户认证与权限控制实战指南
title: 深入Django:用户认证与权限控制实战指南 date: 2024/5/7 18:50:33 updated: 2024/5/7 18:50:33 categories: 后端开发 tags: AuthDecoratorsPermissionsGuardianRESTAuthSessionMgmtMFA 第1章:入门Django与设置 1.1 Django安装与环境配置 在…...

Kubernetes - Dashboard 配置用户名密码方式登录
Kubernetes - Dashboard 配置用户名密码方式登录 前言: 为了 K8s 集群安全,默认情况下 Dashboard 以 Token的形式登录的,那如果我们想以用户名/密码的方式登录该怎么操作呢?其实只需要我们创建用户并进行 ClusterRoleBinding绑定即…...

AIGC能给人类社会带来哪些变革?
随着人工智能技术的飞速发展,AIGC(人工智能生成内容)正在成为推动社会变革的重要力量。本文将从技术角度出发,探讨AIGC技术如何影响和改变人类生活的各个方面。 一、AIGC技术概述 AIGC,即人工智能生成内容࿰…...

医药垃圾分类管理系统|基于SSM医药垃圾分类管理系统的系统设计与实现(源码+数据库+文档)
医药垃圾分类管理系统 目录 基于SSM医药垃圾分类管理系统设计与实现 一、前言 二、系统设计 三、系统功能设计 1系统登录模块 2管理员模块实现 3用户模块实现 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博…...
用vim或gvim编辑程序
vim其实不难使用,学习一下就好了。简单功能很快学会。它有三种模式:命令模式,编辑模式,视模式。打开时在命令模式。在命令模式下按 i 进入编辑模式,在编辑模式下按<Esc>键退出编辑模式。在命令模式按 :wq 保存文…...

linus下Anaconda创建虚拟环境pytorch
一、虚拟环境 1.创建 输入下面命令 conda create -n env_name python3.8 输入y 2.激活环境 输入 conda activate env_name 二、一些常用的命令 在Linux的控制平台 切换到当前的文件夹 cd /根目录/次目录 查看conda目录 conda list 查看pip目录 pip list查看历史命…...

synchronized与volatile关键字
1.synchronized的特性 1.1互斥 synchronized 会起到互斥效果, 某个线程执行到某个对象的 synchronized 中时, 其他线程如果也执行到 同一个对象 synchronized 就会阻塞等待. 进入 synchronized 修饰的代码块, 相当于 加锁 退出 synchronized 修饰的代码块, 相当于 解锁 syn…...

Python基础之运算符操作
在Python中,运算符的作用就是用于执行各种的运算操作,常见的运算符有算数运算符、比较运算符、逻辑运算符、赋值运算符、成员运算符、身份运算符等。下面我们就来看看在Python中这些运算的详细操作。 算术运算符 算术运算符是用来执行一些基本的数学运…...
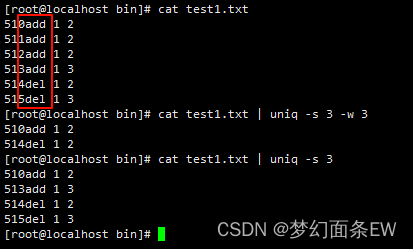
【busybox记录】【shell指令】uniq
目录 内容来源: 【GUN】【uniq】指令介绍 【busybox】【uniq】指令介绍 【linux】【uniq】指令介绍 使用示例: 去除重复行 - 默认输出 去除重复行 - 跳过第n段(空格隔开),比较n1以后的内容,去重 去…...

Nginx从入门到精通速成
文章目录 一. **Nginx** **的简介**1.1 什么是 **nginx**1.2 正向代理1.3 反向代理1.4 **负载均衡**1.5 动静分离 二. **Nginx** **的安装**三. **Nginx** **的常用的命令**四. **Nginx** **的配置文件**五. **Nginx** **配置实例**反向代理实例**1**5.1 实现效果5.2 准备工作5…...

Flutter笔记:Widgets Easier组件库(4)使用按钮组
Flutter笔记 Widgets Easier组件库(4):使用按钮组 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress…...

Docker常用命令 镜像库设置
Docker常用命令 & 镜像库设置 1. 镜像操作2. 容器操作3. 网络操作4. Docker Compose操作5. Docker volume操作6. Docker run介绍7. 镜像库设置 1. 镜像操作 列出本地所有的镜像 docker images从远程仓库拉取镜像到本地 docker pull <image_name>删除本地的指定镜像…...

无人零售,重塑购物新纪元
在这个快节奏的时代,科技的每一次跃进都在悄无声息地改变着我们的生活方式。而今,无人零售正以雷霆之势,颠覆传统购物模式,为我们带来前所未有的便捷与智能体验。想知道无人零售如何彻底改变我们的购物方式吗?跟随我&a…...

【图片格式转换】ICO、JPG、JPEG、PNG图片格式在线免费转换
ICO、JPG、JPEG、PNG图片格式转换 图片格式转换 https://orcc.online 支持ICO、JPG、JPEG、PNG等 主页 https://www.orcc.online 其他工具 pdf在线免费转word文档 https://orcc.online/pdf 时间戳转换 https://orcc.online/timestamp Base64 编码解码 https://orcc.onlin…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...