Python中驼峰命名法和下划线命名法相互转换的实战代码
大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳，不仅形成深入且独到的理解，而且能够帮助新手快速入门。
本文主要介绍了Python中驼峰命名法和下划线命名法相互转换的实战代码，希望能对使用Python的同学们有所帮助。
文章目录
- 1. 问题描述
- 2. 实战代码
1. 问题描述
最近项目涉及到需要将驼峰式的变量命名均转换为下划线的命名的实际需求，可能会有同学会问什么是驼峰式命名，什么又是下划线命名呢？
- 驼峰命名法(Camel Case)：单词的第一个字母小写，之后的每个单词首字母大写。比如myVariable、calculateArea、isEvenNumber。
- 下划线命名法(Snake Case)：所有单词全部小写，单词之间用下划线连接。例如：my_variable、calculate_area、is_even_number。
驼峰命名法在Java、C#等语言中很常见，下划线命名法在Python、C等语言中较为常用。
在经过了亲身的实践后，终于找到了可复现的实战代码，最终将详细的代码总结如下。希望对同学们有所帮助。
相关文章：
Python中驼峰命名法和下划线命名法相互转换的实战代码
大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
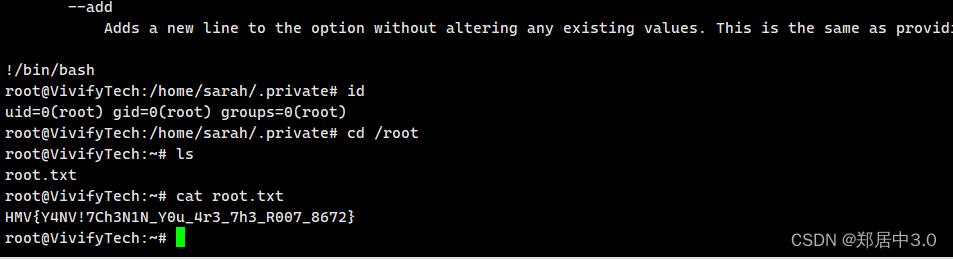
【hackmyvm】vivifytech靶机
渗透思路 信息收集端口扫描端口服务信息目录扫描爆破hydra--sshgit提权 信息收集 ┌──(kali㉿kali)-[~] └─$ fping -ag 192.168.9.0/24 2>/dev/null 192.168.9.119 --主机 192.168.9.164 --靶机个人习惯，也方便后续操作，将IP地址赋值给一个变…...
纯血鸿蒙APP实战开发——手写绘制及保存图片
介绍 本示例使用drawing库的Pen和Path结合NodeContainer组件实现手写绘制功能。手写板上完成绘制后，通过调用image库的packToFile和packing接口将手写板的绘制内容保存为图片，并将图片文件保存在应用沙箱路径中。 效果图预览 使用说明 在虚线区域手写…...
在什么情况下表单会被重复提交？如何避免？
表单被重复提交是Web应用中常见的问题，通常在用户提交表单后点击按钮多次，或在表单提交后刷新页面时发生。这可能导致数据的重复处理，比如重复记录或订单。 何时会发生表单重复提交？ 用户多次点击提交按钮：在网络延迟…...
JavaScript 中的 Class 类
🔥 个人主页：空白诗 文章目录 🔥 引言🎯 基础知识🏗️ 构造函数 (Constructor)🔐 私有字段 (Private Fields)🔐 私有方法 (Private Methods)🧬 继承 (Inheritance)📦 静态…...
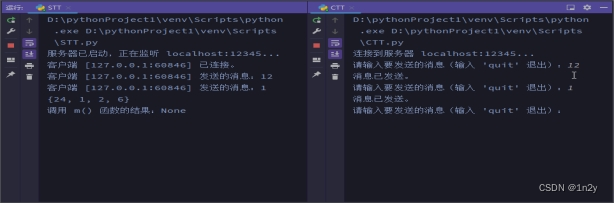
python实验三 实现UDP协议、TCP协议进行服务器端与客户端的交互
实验三 实验题目 1、请利用生成器构造一下求阶乘的函数Factorial()，定义一个函数m()，在m()中调用生成器Factorial()生成小于100的阶乘序列存入集合s中，输出s。 【代码】 def factorial():n1f1while 1: f * n yield (f) n1…...
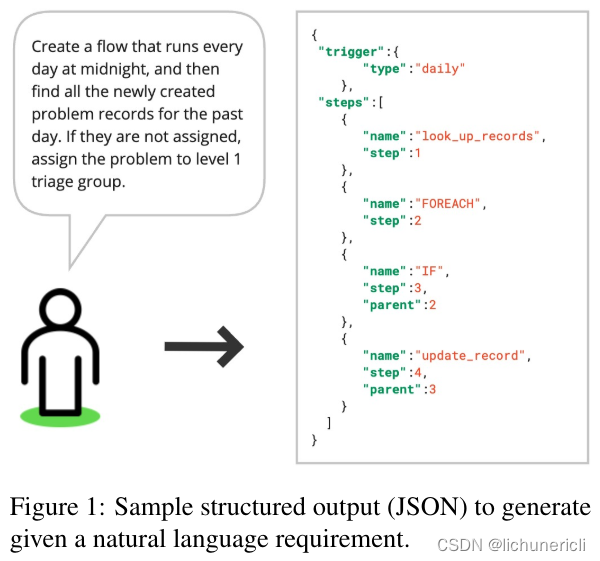
ServiceNow 研究：通过RAG减少结构化输出中的幻觉
论文地址：https://arxiv.org/pdf/2404.08189 原文地址：rag-hallucination-structure-research-by-servicenow 在灾难性遗忘和模型漂移中，幻觉仍然是一个挑战。 2024 年 4 月 18 日 灾难性遗忘： 这是在序列学习或连续学习环境中出现…...
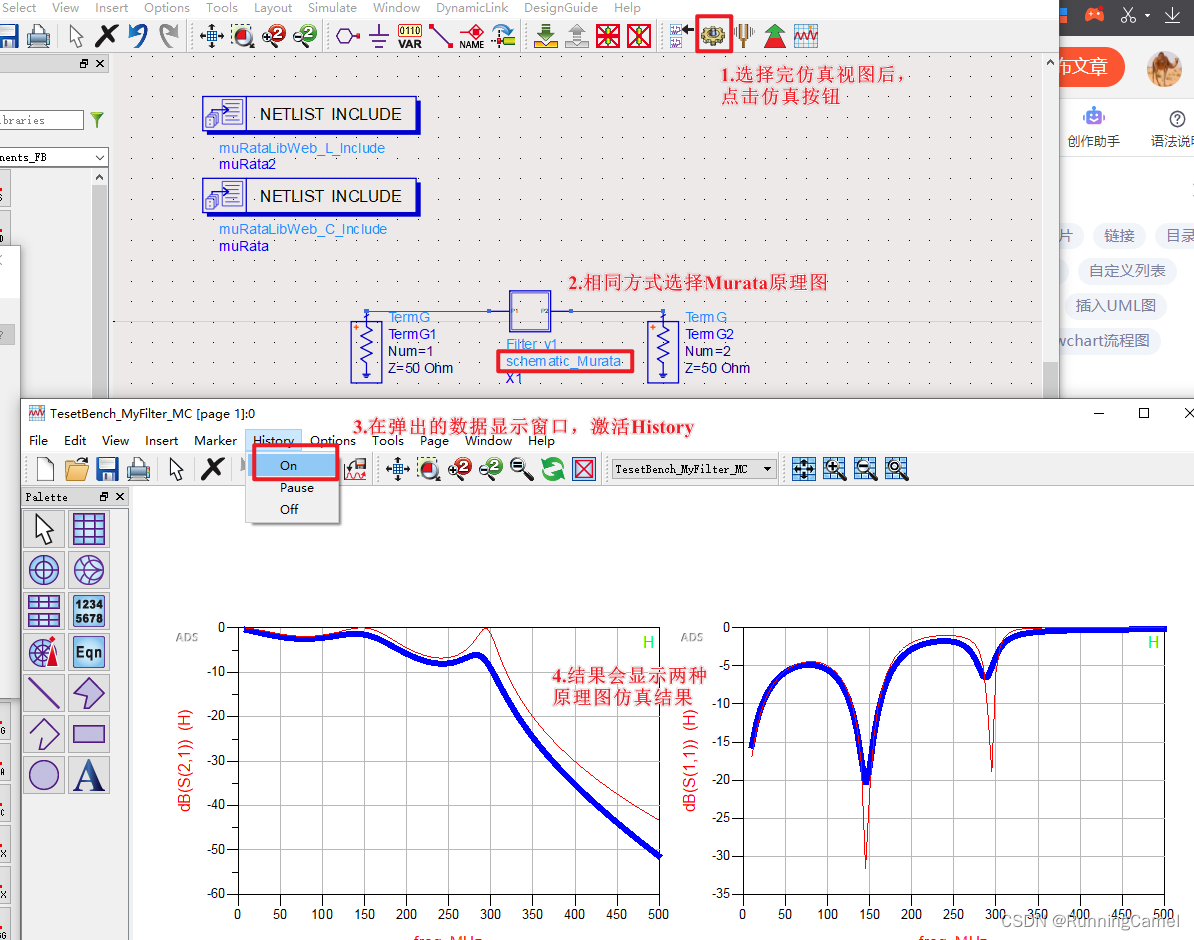
ADS基础教程10-多态性（动态模型选择）
目录 一、多态性定义二、操作步骤１.模型建立２.模型选择３.执行仿真 一、多态性定义 ADS中支持一个Symbol中，可以同时存在多个子图。在仿真时可以动态选择不同的子图继续宁仿真。 二、操作步骤 １.模型建立 在上一章A…...
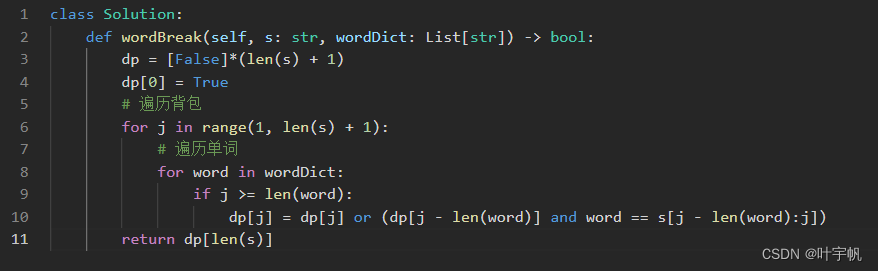
代码随想录第四十六天|单词拆分
题目链接：. - 力扣（LeetCode）...
RabbitMQ的介绍和使用
1.同步通讯和异步通讯 举个例子，同步通讯就像是在打电话，因此它时效性较强，可以立即得到结果，但如果你正在和一个MM打电话，其他MM找你的话，你们之间是不能进行消息的传递和响应的 异步通讯就像是微信&#…...
前端get请求日期类型参数向后端传参失败
1、背景 get请求，通过url上传参，因此日期类型是string类型数据 2、异常信息 nested exception is org.springframework.core.convert.ConversionFailedException: Failed to convert from type [java.lang.String] to type [java.time.LocalDate] for…...
【docker 】 push 镜像提示：denied: requested access to the resource is denied
往 Docker Registry （私服）push 镜像提示：denied: requested access to the resource is denied 镜像push 语法：docker push <registry-host>:<registry-port>/<repository>:<tag> docker push 192.16…...
总结)
浏览器各类好用插件使用及常见问题(技巧)总结
目录 Vimium C快捷键问题为什么Vimium C - 全键盘操作浏览器插件在百度页面中, x ,o,f等快捷键不起作用如何使用viminum c插件进行自定义快捷键?vimucm 为什么在浏览器首页时快捷键不起作用? 网页截图问题firefox 网页截图使用 idm问题浏览器点击idm 不下载? 待续、更新中 V…...
Python批量计算多张遥感影像的NDVI
本文介绍基于Python中的gdal模块，批量基于大量多波段遥感影像文件，计算其每1景图像各自的NDVI数值，并将多景结果依次保存为栅格文件的方法。 如下图所示，现在有大量.tif格式的遥感影像文件，其中均含有红光波段与近红外…...
6.k8s中的secrets资源
一、Secret secrets资源，类似于configmap资源，只是secrets资源是用来传递重要的信息的； secret资源就是将value的值使用base64编译后传输，当pod引用secret后，k8s会自动将其base64的编码，反编译回正常的字符…...
git 更换远程仓库地址三种方法总结
git 更换远程仓库地址三种方法总结 一、前言 由于私服的 gitlab 的地址变更，导致部分项目代码提交不上去，需要修改远端仓地址。 其它需要修改远程仓地址的情况如：切换git clone 协议由ssh变为https。 二、环境 windows 10git version 2.3…...
快速找出存（不存在）在某个（或多个）文件的文件夹
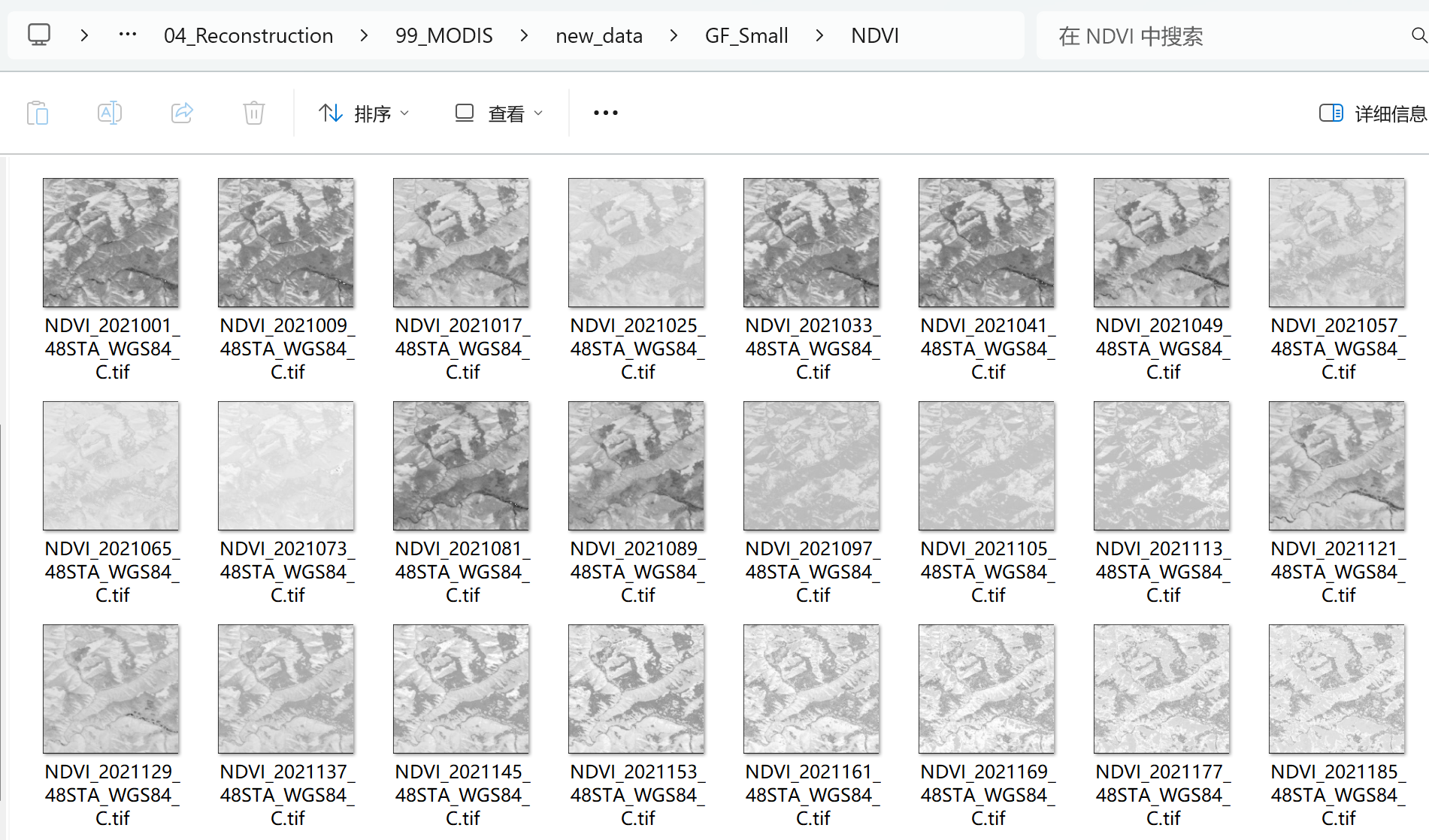
首先，需要用到的这个工具： 度娘网盘 提取码：qwu2 蓝奏云 提取码：2r1z 想要找出有下面这个文件存在的文件夹 切换到批量文件复制版块，快捷键Ctrl5 右侧，搜索添加 选定范围，勾选搜索文件夹、包…...
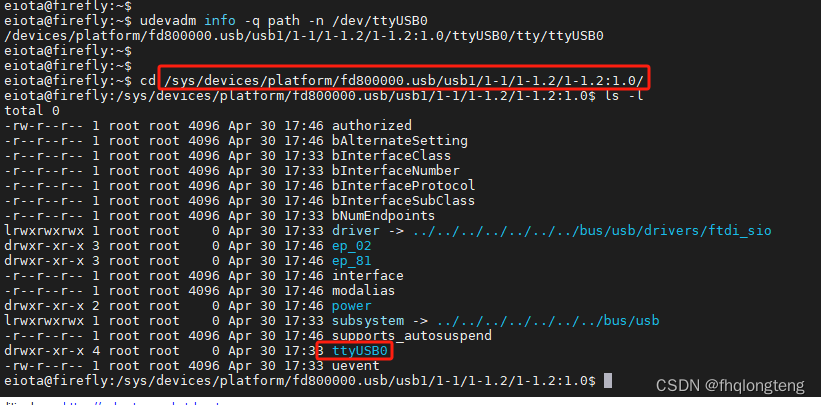
Linux USB转串口设备路径的查找方法
1、USB转串口设备 USB转串口设备是在嵌入式软件开发过程中经常要使用的，常常用于对接各种各样的串口设备。如果一台linux主机上使用多个usb转串口设备时，应用程序中就需要知道自己操作的是哪个串口设备。串口设备在系统上电时，由于驱动加载的…...
【初阶数据结构】单链表之环形链表
目录标题 前言环形链表的约瑟夫问题环形链表环形链表|| 前言 前面我们已经学习了关于单链表的一些基本东西，今天我们来学习单链表的一个拓展——环形链表，我们将用力扣和牛客网上的三道题目来分析讲解环形链表问题。 环形链表的约瑟夫问题 我们首先来看…...
【积分，微分，导数，偏导数公式推导】
1. 积分 积分是微积分的一个分支，用于计算曲边梯形的面积或者变速直线运动的总距离等。积分分为不定积分和定积分。 不定积分：给出一个函数，求出其所有可能的原函数。定积分：计算一个函数在特定区间上的积分。 2. 微分 微分是…...
基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容：参考网站： PID算法控制 PID即：Proportional（比例）、Integral（积分&…...
VB.net复制Ntag213卡写入UID
本示例使用的发卡器：https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
【位运算】消失的两个数字（hard）
消失的两个数字（hard） 题⽬描述：解法（位运算）：Java 算法代码：更简便代码 题⽬链接：⾯试题 17.19. 消失的两个数字 题⽬描述： 给定⼀个数组，包含从 1 到 N 所有…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧！！！非常感谢！！持续更新！！！ 🚀 AI篇持续更新中！（长期更新） 目前2025年06月05日更新到： AI炼丹日志-28 - Aud…...
学习STC51单片机31（芯片为STC89C52RCRC）OLED显示屏1
每日一言 生活的美好，总是藏在那些你咬牙坚持的日子里。 硬件：OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写，"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
以光量子为例，详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学（silicon photonics）的光波导（optical waveguide）芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中，光既是波又是粒子。光子本…...
九天毕昇深度学习平台 | 如何安装库？
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子： 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式：Python 中的懒加载与自定义初始化参数 在软件开发中，单例模式（Singleton Pattern）是一种常见的设计模式，确保一个类仅有一个实例，并提供一个全局访问点。在多线程环境下，实现单例模式时需要注意线程安全问题，以防止多个线程同时创建实例，导致…...