【Kotlin】Java三目运算转成 kotlin 表达
这行代码会直接计算 array.size == 1 的布尔值,并将其赋值给 result。在 Kotlin 中,不需要使用三元操作符,因为条件表达式本身就返回一个布尔值 java 中三木运算:
int [] array = new int[]{1, 2, 3, 4, 5}; boolean test = array >1 true :false;在 Kotlin 中,你可以使用类似的表达式来检查数组的长度是否大于 1。Kotlin 中的数组长度可以通过 size 属性来获取,而不是像 Java 中的 length() 方法。
val result = array.size > 1这里直接使用 array.size > 1 就可以返回一个布尔值(true 或 false),所以不需要使用三元操作符(Kotlin 本身不支持传统的三元操作符 ? :,而是可以使用 if-else 表达式)
val result = array.size == 1在 Kotlin 中,你可以直接使用条件表达式来检查数组的长度是否等于 1。如同之前提到的,Kotlin 使用 size 属性来获取数组的长度
相关文章:

【Kotlin】Java三目运算转成 kotlin 表达
这行代码会直接计算 array.size 1 的布尔值,并将其赋值给 result。在 Kotlin 中,不需要使用三元操作符,因为条件表达式本身就返回一个布尔值 java 中三木运算: int [] array new int[]{1, 2, 3, 4, 5}; boolean test array &g…...

如何安全可控地进行内外网跨网络传输文件?
跨网络传输文件通常指的是在不同的网络环境之间移动数据,这在现代企业运营中非常常见。随着网络技术的高速发展,为了有效地保护内部的核心数据资产,企业一般会采用内外网隔离的策略。在进行内外网跨网络传输文件时,需要考虑多种因…...

Python Json数据解析
本篇主要介绍Python 中json数据如何解析、转化、保存和加载。 目录 Json数据解析 概念 作用 Json文件组成 Json转化为Python数据类型 Python数据类型转化为json 写入本地json文件 读取本地的json文件 总结 Json数据解析 概念 一种保存数据的格式 作用 可以保存本地…...

pyinstaller打包pytorch和transformers程序
记录使用pyinstaller打包含有pytorch和transformers库的程序时遇到的问题和解决方法。 环境和版本信息 操作系统:Windows 11 Python:3.10.12 pyinstaller:5.13.0 torch:2.2.2 transformers:4.40.1 打包过程和问…...
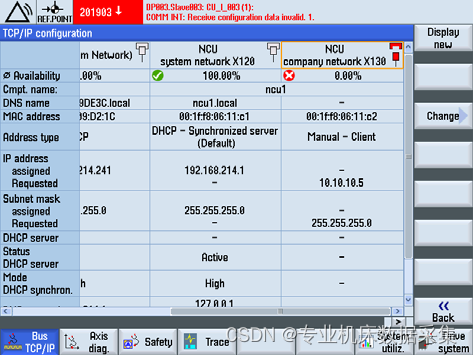
西门子数控网络IP设定配置
总结:menuselect-诊断-屏幕下方右翻页找到tcp/ip,进去选择tcp/ip诊断,进去选择x130网口,点击更改, 如果没有更改,menuselect-调试-口令,输入口令 sunrise 然后重新配置tcp/ip,配置完…...

[Unity]备份许可文件
原因:因Unity需要重新恢复出厂设置,所以需要先将许可文件本分到本地,以便重新初始化后输入许可。 1)登录管理网络web界面,在服务页面打开SSH 2)ssh到管理网络,使用service用户登录 3…...
第十五届蓝桥杯省赛大学B组(c++)
很幸运拿了辽宁赛区的省一,进入6月1号的国赛啦... 这篇文章主要对第十五届省赛大学B组(C)进行一次完整的复盘,这次省赛2道填空题6道编程题: A.握手问题 把握手情景看成矩阵: 粉色部分是7个不能互相捂手的情况 由于每个人只能和其他人捂手, 所以黑色情况是不算的 1和2握手2和…...
Python Flask框架(一)初识Flask
Flask是使用Python编写的Web微框架。Web框架可以使我们不用关心底层的请求响应处理,更方便高效的编写Web程序。Flask有两个主要依赖,一个是WSGI(Web Server Gateway Interface,web服务器网关接口)工具集,另…...
VS2022 .Net6.0 无法打开窗体设计器
拿Vs2022 建了个Demo,运行环境是net6.0-windows,无论双击或是右键都打不开窗体设计器 打开项目目录下的*.csproj.user <?xml version"1.0" encoding"utf-8"?> <Project ToolsVersion"Current" xmlns"htt…...
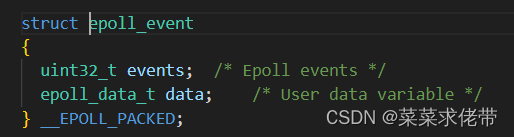
Linux学习之高级IO
之前的内容我们基本掌握了基础IO,如套接字,文件描述符,重定向,缓冲区等知识都是文的基本认识,而高级IO则是指更加高效的IO。 对于应用层,在读写的时候,本质就是把数据写给OS,若一方…...

一分钟了解Polysciences PEI 40K转染试剂的原理
在细胞实验中,细胞转染大概是最常用、最基础的实验技能。转染细胞的方法很多,而PEI作为带有高电荷阳离子的多聚物,非常容易结合带负电荷的DNA分子,形成复合物,在HEK293和CHO等细胞中转染效率较高,常用于大规…...

Clickhouse IP 函数
IPv4NumToString(num) 将数字类型ip转换为IPv4格式。 Takes a UInt32 number. Interprets it as an IPv4 address in big endian. Returns a string containing the corresponding IPv4 address in the format A.B.C.d (dot-separated numbers in decimal form). Alias: …...
)
【Python】numpy.ptp()
numpy.ptp() 函数是 NumPy 库中的一个有用函数,用于计算数组中的“峰到峰”(peak-to-peak)值,即数组中的最大值与最小值之差。这个函数可以帮助快速评估数组中数据的变化范围,常用于信号处理、数据分析等领域中&#x…...

The provided password or token is incorrect or your account
IDEA使用git技巧 【/n】 01 问题出现场景 我的gitlab上个月生成的token到期了,于是今天推上去的时候报了这个错误 The provided password or token is incorrect or your account has 2FA enabled and you must use a personal access token instead of a password. See ht…...

常见的shell命令
以下是一些常见的shell命令: cd:改变当前目录;ls:列出目录中的文件和子目录;mkdir:创建一个新的目录;touch:创建一个新的空文件或更新已存在的文件的时间戳;rmÿ…...

堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41),framework修改,去除第三方app的倒计时页面
文章目录 堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41),framework修改,去除第三方app的倒计时页面1.打印异常堆栈2.去除第三方app的倒计时页面3.模拟点击事件跳过首页进入主页 堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41)&#x…...

只允许内网访问时,如何设置hosts
1、Hosts文件简介 hosts文件是一个没有扩展名的计算机文件,用于将主机名与对应的 IP 地址关联起来。在操作系统中,hosts文件通常用于在本地解析域名,以便将域名映射到特定的IP地址。这个文件可以用来屏蔽广告、加速访问特定网站、解决DNS解析…...
nature《自然》期刊文献怎么在家查看下载
nature《自然》期刊我们都知道,是世界上历史悠久的、最有名望的科学杂志之一。下载该期刊文献是需要使用权限的,如果你没有nature《自然》期刊的资源,又该如何获取呢?请看本文的经验分享。 一、先百度“文献党下载器” 在文献党下…...

python作业五
题目:注册登录 制作一个注册登录模块 注册:将用户填入的账户和密码保存到一个文件(users.bin) 登陆:将用户填入账户密码和users.bin中保存的账户密码进行比对,如果账户和密码完全相同 那 么登录成功,否则登录失败…...

经典的设计模式和Python示例(一)
目录 一、工厂模式(Factory Pattern) 二、单例模式(Singleton Pattern) 三、观察者模式(Observer Pattern) 一、工厂模式(Factory Pattern) 工厂模式(Factory Pattern…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
