力扣每日一题108:将有序数组转换为二叉搜索树
题目
简单
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡
二叉搜索树。
示例 1:
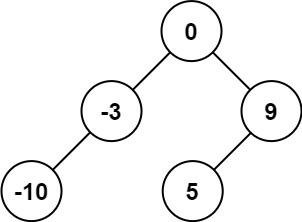
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
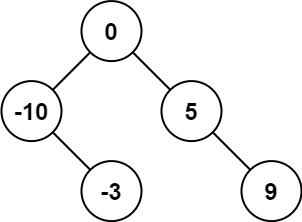
示例 2:
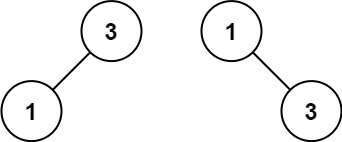
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
面试中遇到过这道题?
1/5
是
否
通过次数
471.9K
提交次数
601.7K
通过率
78.4%
思路
平衡二叉搜索树有两个要求
1、每个节点左右子树的高度差不能超过1
2、每个节点的大于所有左子树结点,小于所有右子树结点。
要满足第一个条件的话,我们可以递归建树,每次将中间的值作为根节点,然后递归调用左右两部分。
要满足第二个条件,只需将root->left指向左边部分递归的结果,root->right指向右边部分递归的结果即可。
代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode *creat(int lo,int hi,vector<int>& nums){if(lo>hi) return NULL;int mid=(lo+hi)/2;TreeNode *root=new TreeNode;root->val=nums[mid];root->left=creat(lo,mid-1,nums);root->right=creat(mid+1,hi,nums);return root;}TreeNode* sortedArrayToBST(vector<int>& nums) {int lo=0,hi=nums.size()-1;TreeNode *root=creat(lo,hi,nums);return root;}
};相关文章:

力扣每日一题108:将有序数组转换为二叉搜索树
题目 简单 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也…...

保护公司机密:避免员工带着数据说拜拜
公司的核心资产之一就是数据。无论是客户信息、研发代码、内部决议、财务报告、商业合同、设计图纸等都是公司的重要资产。如果这些数据在员工离职时被带走,或在员工在职期间不当行为导致数据泄露,将给公司带来重大损失。 然而,保护这些数据…...
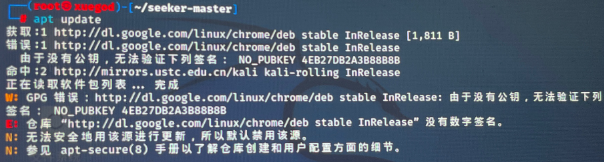
kali apt update报错
错误信息: 获取:http:/dl.google.com/几inux/chrome/.deb stable InRelease 错误:http:/dl.google.com/linux/chrome/deb stable InRelease 由于没有公钥,无法验证下列签名:NO_PUBKEY4EB27DB2A3B88B8B 命中:…...

7-1 图图图
某城市有n个景点,部分景点之间有巴士免费来回接送。(1) 给定某个景点x,如果从这个景点出发坐一次免费巴士,可以到达多少个不同的景点?(2) 判断景点a是否可以通过免费巴士(可换乘)到达景点b;(3) …...
)
Java(多线程)
取水: 主部分: package a0506.Test3;import java.util.Random;public class Test3 {public static void main(String[] args) {Well2 well2new Well2(10);WellThread Zsnew WellThread("------张三------",well2,new Random().nextInt(5));W…...

程序员必备的7大神器,效率飞起!
我们都知道程序员在工作时,会经常遇到任务繁重的情况,为了提高效率,程序员们也会借助一些软件,那么哪些软件可以帮助程序员们提高工作效率呢? 整理不易,关注一波!! 1. Xftp 7 Xft…...
揭秘文件加密利器:24年度最值得信赖的5大加密软件评测
数据安全与隐私保护已成为我们每个人都必须面对的重要问题。 文件加密软件作为保障数据安全的关键工具,其重要性不言而喻。 在众多的加密软件中,哪些软件能够在保障数据安全的同时,又具备良好的易用性和稳定性呢? 本文将为您揭秘…...
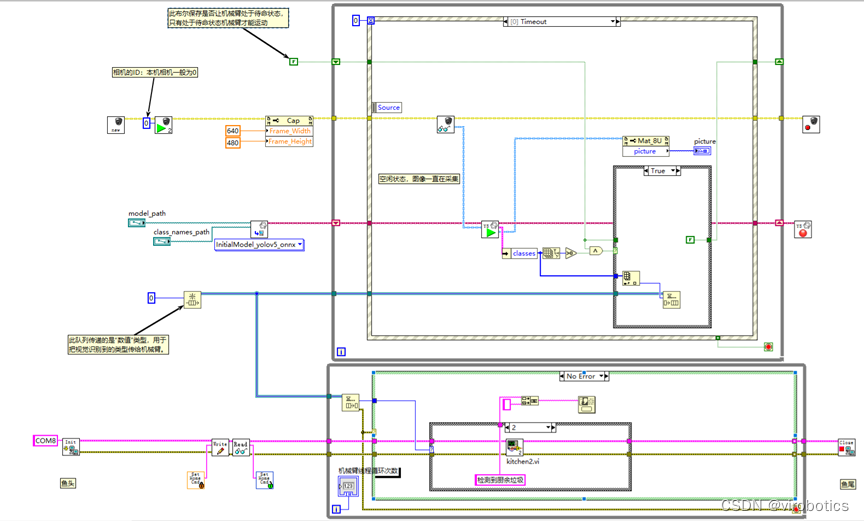
【仪酷LabVIEW AI工具包案例】使用LabVIEW AI工具包+YOLOv5结合Dobot机械臂实现智能垃圾分类
🏡博客主页: virobotics(仪酷智能):LabVIEW深度学习、人工智能博主 🎄所属专栏:『仪酷LabVIEW AI工具包案例』 📑上期文章:『【YOLOv9】实战二:手把手教你使用TensorRT实现YOLOv…...

鸿蒙应用开发系列 EX篇:HarmonyOS应用开发者基础认证
文章目录 系列文章背景认证考试题库参考注意:题库会不定时的进行具备调整甚至整体轮换,此为2024.5月版本注意:题库中题目的选项每次都会随机顺序,请参考内容判断题单选题多选题系列文章 鸿蒙应用开发系列 篇一:鸿蒙系统概述 鸿蒙应用开发系列 篇二:鸿蒙系统开发工具与环…...

基于Linux中的 进程相关知识 综合讲解
目录 一、进程的基本概念 二、pid,ppid,fork函数 三、进程的状态讲解 四、进程的优先级 五、完结撒❀ 一、进程的基本概念 概念: ● 课本概念:程序的一个执行实例,正在执行的程序等 ● 内核观点:担当…...
前端高频面试题 5.08
事件委托 事件委托是前端开发中常用的一种优化性能和代码可维护性的方法,它基于DOM的事件冒泡机制。当一个元素触发事件时,这个事件会按照从顶层到底层的顺序传播,直到最底层的元素(通常是文档的根节点)。事件委托利用…...

python 的继承、封装和多态
1. 继承(Inheritance) 继承是面向对象编程中的一个重要概念,它允许一个类(子类)继承另一个类(父类)的属性和方法。子类可以重用父类的代码,同时也可以扩展或修改父类的行为。 常用…...

数智结合,智慧合同让法务管理发挥内在价值
在当今这个信息化、数字化飞速发展的时代,数据已成为企业重要的战略资源。法务管理作为企业内部控制和风险防范的重要环节,其重要性不言而喻。然而,传统的法务管理模式往往存在效率低下、信息孤岛、反应迟缓等问题。在这样的背景下࿰…...

Ubuntu 安装docker
1: 卸载旧版本 如果你曾经安装过旧版本的 Docker,首先需要卸载它们: sudo apt-get remove docker docker-engine docker.io containerd runc2: 安装依赖工具 安装一些必要的工具,以便后续的安装过程能够顺利进行: sudo apt-ge…...

【北京迅为】《iTOP-3588开发板快速烧写手册》-第8章 TF启动
RK3588是一款低功耗、高性能的处理器,适用于基于arm的PC和Edge计算设备、个人移动互联网设备等数字多媒体应用,RK3588支持8K视频编解码,内置GPU可以完全兼容OpenGLES 1.1、2.0和3.2。RK3588引入了新一代完全基于硬件的最大4800万像素ISP&…...

Helm 模板流程控制
Helm 的模板语言提供了多种控制结构,以允许模板作者根据条件逻辑生成模板内容。以下是 Helm 模板控制结构的核心内容总结: 控制结构 Helm 模板支持以下控制结构: if/else:用于创建条件语句,根据给定的条件包含或排除…...

Kansformer?变形金刚来自过去的新敌人
1.前言 多层感知器(MLPs),也被称为全连接前馈神经网络,是当今深度学习模型的基础组成部分。 MLPs在机器学习中扮演着至关重要的角色,因为它们是用于近似非线性函数的默认模型,这得益于通用近似定理所保证的表达能力。然而,MLPs真的是我们能构建的最佳非线性回归器吗?尽管ML…...

今晚 19:00 | 从这两个问题入手,带你了解数据要素相关税务问题
五一假期已经结束,返工后当然是继续劳动啦~数据要素系列直播《星光对话》第三期也将在今晚19:00,继续跟大家见面。 本期直播,依然由 星光数智咨询总监 刘靖 主讲,带来:《数据要素相关税务问题解读》。 主要围绕两个问题…...

《QT实用小工具·五十一》带动画的 CheckBox
1、概述 源码放在文章末尾 该项目实现了带动画效果的多选框,鼠标放在上面或者选中都会呈现炫酷的动画效果,demo演示如下: 项目部分代码如下所示: #ifndef LINEARCHECKBOX_H #define LINEARCHECKBOX_H#include <QCheckBox> …...

PDT(police digital trunking )警用数字集群射频指标及测试方法
天线端口----测试传导 机箱端口----测试辐射 基本概念 传导测试方法 VBW3RBW 仪器设置 辐射测试方法...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
