当前位置： 首页 > news >正文

Hydroxyethyl-PEG-Hydroxyethyl，Hy-PEG-Hy是一种由聚乙二醇（PEG）和二酰肼单元构成的嵌段共聚物

news 2025/7/5 18:21:03

【试剂详情】

英文名称

Hydroxyethyl-PEG-Hydroxyethyl，Hy-PEG-Hy

中文名称

聚乙二醇二酰肼，酰肼 PEG 酰肼

外观性状

由分子量决定，固体或者液体。

分子量

0.4k，0.6k，1k，2k，3.4k，5k，10k（可定制）

溶解性

溶于水，

溶于DMF、DMSO等部分有机溶液

规格

可按需包装定制

纯度

95%+

储存条件

干燥、避光，温度不超-20℃

注意事项

现配现用，不可频繁解冻

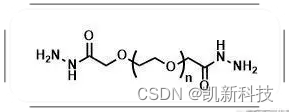
【结构式】西安凯新生物科技Hy-PEG-Hy结构式

【试剂介绍】

Hy-PEG-Hy，即聚乙二醇二酰肼，是一种由聚乙二醇（PEG）和二酰肼单元构成的嵌段共聚物。在Hy-PEG-Hy分子中，PEG链段起到了至关重要的作用，它赋予整个分子良好的生物相容性和水溶性。Hy是Hydroxyethyl的缩写，这是一种具有亲水性的化学基团，能够与许多其他化学基团进行反应。在Hy-PEG-Hy中，Hy基团位于PEG的两端，使得整个分子既具有亲水性又具有疏水性，从而能够与许多不同的分子进行反应。

【相关试剂】

Hydroxy-PEG2-CH2CO2tBu
Hydroxy-PEG2-CH2-Boc
149299-82-1
Hydroxy-PEG6-CH2CO2tBu
Hydroxy-PEG6-CH2-Boc
297162-47-1
Hydroxy-PEG5-CH2CO2tBu
Hydroxy-PEG5-CH2-Boc
1807530-05-7
Hydroxy-PEG3-CH2CO2tBu
Hydroxy-PEG3-CH2-Boc
518044-31-0
Hydroxy-PEG4-CH2CO2tBu
Hydroxy-PEG4-CH2-Boc
169751-72-8
Hydroxy-PEG1-CH2CO2tBu
Hydroxy-PEG1-CH2-Boc
287174-32-7
m-PEG10-alcohol
DecaetHylene glycol monometHyl ether
27425-92-9
Hydroxy-PEG2-acid sodium salt
Hydroxy-PEG2-acid
1334286-77-9
m-PEG4-benzaldeHyde
153364-63-7
Hydroxy-PEG4-CH2CO2H sodium salt
Hydroxy-PEG4-CH2COOH
70678-95-4
Hydroxy-PEG2-CH2CO2H sodium salt
Hydroxy-PEG2-CH2COONa
51951-04-3

注：该试剂仅用于的科学研究，不能用于人体实验或其他治疗型用途。

本文试剂资料由西安凯新生物科技有限公司小华编辑整理。

相关文章：

Hydroxyethyl-PEG-Hydroxyethyl，Hy-PEG-Hy是一种由聚乙二醇（PEG）和二酰肼单元构成的嵌段共聚物

【试剂详情】 英文名称 Hydroxyethyl-PEG-Hydroxyethyl，Hy-PEG-Hy 中文名称 聚乙二醇二酰肼，酰肼 PEG 酰肼 外观性状 由分子量决定，固体或者液体。 分子量 0.4k，0.6k，1k，2k，3.4k&#xf…...

编程日记 2024/5/8 19:45:25

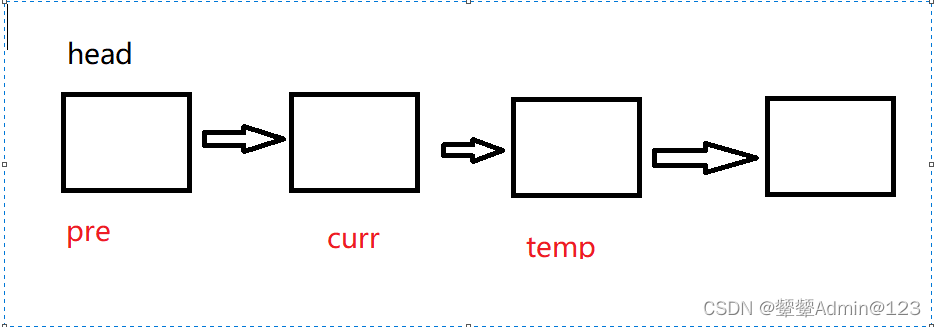
链表面试题目：反转一个单链表的两种方法（解析＋代码）

我们继续来看一下单链表的题目和代码吧，把学习的知识运用到实际中，大家加油 先看OJ题目 OJ题目（反转单链表） 双指针法 1.创建两个指针，为pre curr，curr指向头结点，curr用来遍历链表 2.curr指向…...

编程日记 2024/5/8 19:44:23

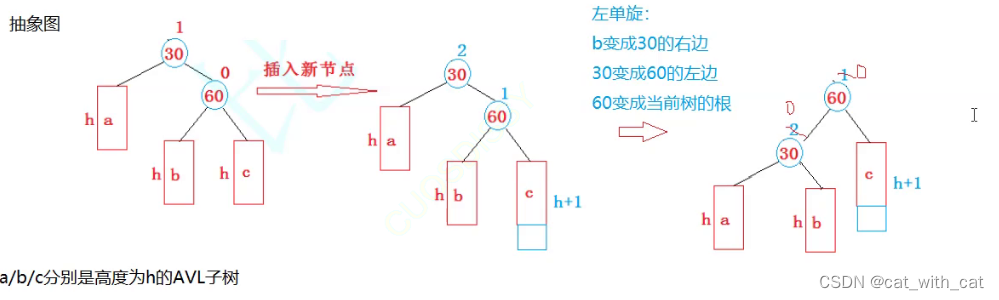
[C++][数据结构]AVL树插入的模拟实现

前言 紧接着上一篇文章，我们来模拟实现一下set的底层结构 引入 对于BSTree，虽然可以缩短查找的效率，但如果数据有序它将退化为单支树 我们可以用AVL树来解决这个问题。 概念 AVL树： 它的每个结点的左右子树高度之差的绝对值…...

编程日记 2024/5/8 19:43:22

力扣每日一题108：将有序数组转换为二叉搜索树

题目 简单 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。 示例 1： 输入：nums [-10,-3,0,5,9] 输出：[0,-3,9,-10,null,5] 解释：[0,-10,5,null,-3,null,9] 也…...

编程日记 2024/5/8 19:42:21

保护公司机密：避免员工带着数据说拜拜

公司的核心资产之一就是数据。无论是客户信息、研发代码、内部决议、财务报告、商业合同、设计图纸等都是公司的重要资产。如果这些数据在员工离职时被带走，或在员工在职期间不当行为导致数据泄露，将给公司带来重大损失。 然而，保护这些数据…...

编程日记 2024/5/8 19:41:20

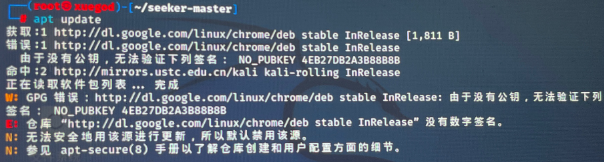
kali apt update报错

错误信息： 获取：http:/dl.google.com/几inux/chrome/.deb stable InRelease 错误：http:/dl.google.com/linux/chrome/deb stable InRelease 由于没有公钥，无法验证下列签名：NO_PUBKEY4EB27DB2A3B88B8B 命中&#xff1a…...

编程日记 2024/5/8 19:39:17

7-1 图图图

某城市有n个景点，部分景点之间有巴士免费来回接送。(1) 给定某个景点x，如果从这个景点出发坐一次免费巴士，可以到达多少个不同的景点？(2) 判断景点a是否可以通过免费巴士（可换乘）到达景点b；(3) …...

编程日记 2024/5/8 19:36:13

Java（多线程)

取水： 主部分： package a0506.Test3;import java.util.Random;public class Test3 {public static void main(String[] args) {Well2 well2new Well2(10);WellThread Zsnew WellThread("------张三------",well2,new Random().nextInt(5));W…...

编程日记 2024/5/8 19:35:12

程序员必备的7大神器，效率飞起！

我们都知道程序员在工作时，会经常遇到任务繁重的情况，为了提高效率，程序员们也会借助一些软件，那么哪些软件可以帮助程序员们提高工作效率呢？ 整理不易，关注一波！！ 1. Xftp 7 Xft…...

编程日记 2024/5/8 19:34:10

揭秘文件加密利器:24年度最值得信赖的5大加密软件评测

数据安全与隐私保护已成为我们每个人都必须面对的重要问题。 文件加密软件作为保障数据安全的关键工具，其重要性不言而喻。 在众多的加密软件中，哪些软件能够在保障数据安全的同时，又具备良好的易用性和稳定性呢？ 本文将为您揭秘…...

编程日记 2024/5/8 19:33:09

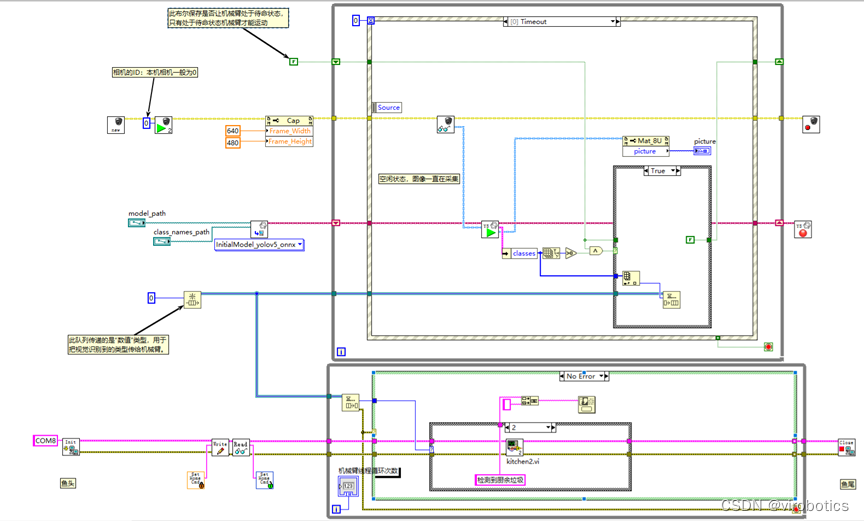
【仪酷LabVIEW AI工具包案例】使用LabVIEW AI工具包+YOLOv5结合Dobot机械臂实现智能垃圾分类

‍‍🏡博客主页： virobotics(仪酷智能)：LabVIEW深度学习、人工智能博主 🎄所属专栏：『仪酷LabVIEW AI工具包案例』 📑上期文章：『【YOLOv9】实战二：手把手教你使用TensorRT实现YOLOv…...

编程日记 2024/5/8 19:32:08

鸿蒙应用开发系列 EX篇：HarmonyOS应用开发者基础认证

文章目录 系列文章背景认证考试题库参考注意：题库会不定时的进行具备调整甚至整体轮换，此为2024.5月版本注意：题库中题目的选项每次都会随机顺序，请参考内容判断题单选题多选题系列文章 鸿蒙应用开发系列 篇一：鸿蒙系统概述 鸿蒙应用开发系列 篇二：鸿蒙系统开发工具与环…...

编程日记 2024/5/8 19:29:05

基于Linux中的 进程相关知识 综合讲解

目录 一、进程的基本概念 二、pid，ppid，fork函数 三、进程的状态讲解 四、进程的优先级 五、完结撒❀ 一、进程的基本概念 概念： ● 课本概念：程序的一个执行实例，正在执行的程序等 ● 内核观点：担当…...

编程日记 2024/5/8 19:28:03

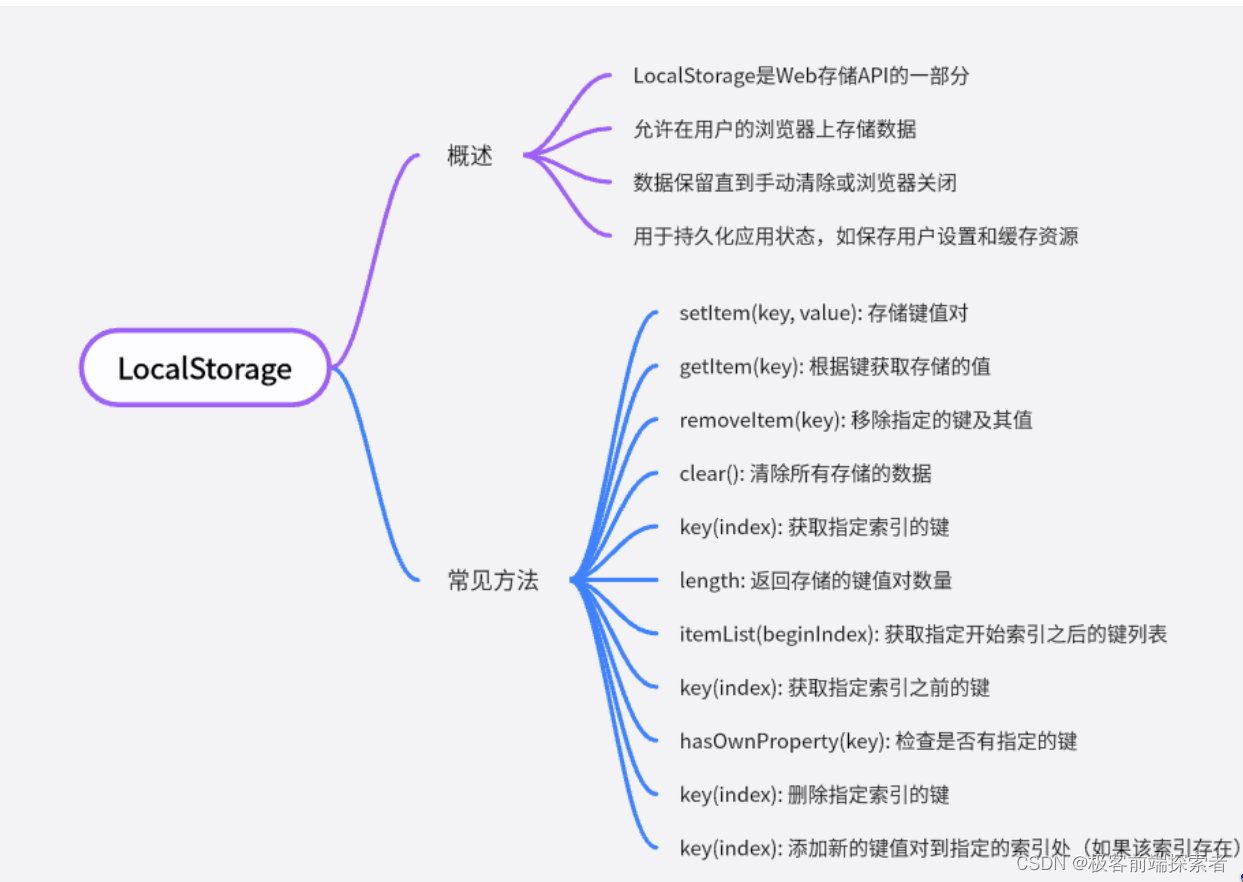
前端高频面试题 5.08

事件委托 事件委托是前端开发中常用的一种优化性能和代码可维护性的方法，它基于DOM的事件冒泡机制。当一个元素触发事件时，这个事件会按照从顶层到底层的顺序传播，直到最底层的元素（通常是文档的根节点）。事件委托利用…...

编程日记 2024/5/8 19:25:01

python 的继承、封装和多态

1. 继承（Inheritance） 继承是面向对象编程中的一个重要概念，它允许一个类（子类）继承另一个类（父类）的属性和方法。子类可以重用父类的代码，同时也可以扩展或修改父类的行为。 常用…...

编程日记 2024/5/8 19:22:59

数智结合，智慧合同让法务管理发挥内在价值

在当今这个信息化、数字化飞速发展的时代，数据已成为企业重要的战略资源。法务管理作为企业内部控制和风险防范的重要环节，其重要性不言而喻。然而，传统的法务管理模式往往存在效率低下、信息孤岛、反应迟缓等问题。在这样的背景下&#xff0…...

编程日记 2024/5/8 19:19:55

Ubuntu 安装docker

1: 卸载旧版本 如果你曾经安装过旧版本的 Docker，首先需要卸载它们： sudo apt-get remove docker docker-engine docker.io containerd runc2: 安装依赖工具 安装一些必要的工具，以便后续的安装过程能够顺利进行： sudo apt-ge…...

编程日记 2024/5/8 19:17:53

【北京迅为】《iTOP-3588开发板快速烧写手册》-第8章 TF启动

RK3588是一款低功耗、高性能的处理器，适用于基于arm的PC和Edge计算设备、个人移动互联网设备等数字多媒体应用，RK3588支持8K视频编解码，内置GPU可以完全兼容OpenGLES 1.1、2.0和3.2。RK3588引入了新一代完全基于硬件的最大4800万像素ISP&…...

编程日记 2024/5/8 19:16:51

Helm 模板流程控制

Helm 的模板语言提供了多种控制结构，以允许模板作者根据条件逻辑生成模板内容。以下是 Helm 模板控制结构的核心内容总结： 控制结构 Helm 模板支持以下控制结构： if/else：用于创建条件语句，根据给定的条件包含或排除…...

编程日记 2024/5/8 19:15:50

Kansformer?变形金刚来自过去的新敌人

​1.前言 多层感知器(MLPs),也被称为全连接前馈神经网络,是当今深度学习模型的基础组成部分。 MLPs在机器学习中扮演着至关重要的角色,因为它们是用于近似非线性函数的默认模型,这得益于通用近似定理所保证的表达能力。然而,MLPs真的是我们能构建的最佳非线性回归器吗?尽管ML…...

编程日记 2024/5/8 19:14:49

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2025/7/5 9:34:51

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2025/7/4 6:15:03

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/6/19 11:42:45

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2025/6/29 18:40:59

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/6/17 6:27:36

抖音增长新引擎：品融电商，一站式全案代运营领跑者

抖音增长新引擎&#xff1a;品融电商&#xff0c;一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中&#xff0c;品牌如何破浪前行&#xff1f;自建团队成本高、效果难控&#xff1b;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

编程新知 2025/7/5 8:48:15

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2025/6/20 11:32:51

WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）

一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解&#xff0c;适合用作学习或写简历项目背景说明。 &#x1f9e0; 一、概念简介&#xff1a;Solidity 合约开发 Solidity 是一种专门为 以太坊&#xff08;Ethereum&#xff09;平台编写智能合约的高级编…...

编程新知 2025/6/21 12:34:41

12.找到字符串中所有字母异位词

&#x1f9e0; 题目解析 题目描述&#xff1a; 给定两个字符串 s 和 p&#xff0c;找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义&#xff1a; 若两个字符串包含的字符种类和出现次数完全相同&#xff0c;顺序无所谓&#xff0c;则互为…...

编程新知 2025/7/5 5:31:34

多模态大语言模型arxiv论文略读（108）

CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题&#xff1a;CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者&#xff1a;Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

编程新知 2025/7/5 8:54:59