算法提高之树的中心
算法提高之树的中心
-
核心思想:树形dp + 换根dp
-
每个点作为根节点 找其子树的最大距离和父节点的最大距离
-
dfs1:求子树对于当前根节点的最大距离和次大距离
- 求次大距离原因:如果当前节点是其父节点子树的最大路径上的点,最大距离不能用

-
dfs2:找父节点以上的最长距离
-
-
#include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 10010,M=N<<1,INF=0x3f3f3f3f;int n;int h[N],e[M],ne[M],w[M],idx;int d1[N],d2[N],up[N];int s1[N],s2[N]; //s1存该点最大距离从哪个点过来 s2存次大距离...void add(int a, int b, int c){e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;}void dfs1(int u,int father){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j == father) continue;dfs1(j,u);if(d1[j] + w[i] >= d1[u]){d2[u] = d1[u],d1[u] = d1[j]+w[i];s2[u] = s1[u],s1[u] = j;}else if(d1[j] + w[i]> d2[u]){d2[u] = d1[j]+w[i] , s2[u] = j;}}}void dfs2(int u,int father){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==father) continue;//如果j为求最大距离时用的点 d1[u]不能用if(s1[u] == j) up[j] = w[i] + max(up[u],d2[u]); else up[j] = w[i] + max(up[u],d1[u]);dfs2(j,u);}}int main(){memset(h,-1,sizeof h);cin>>n;for(int i=1;i<n;i++){int a,b,c;cin>>a>>b>>c;add(a,b,c) , add(b,a,c);}dfs1(1,-1);dfs2(1,-1);int res=INF;for(int i=1;i<=n;i++) res = min(res,max(d1[i],up[i]));cout<<res<<endl;}
相关文章:

算法提高之树的中心
算法提高之树的中心 核心思想:树形dp 换根dp 每个点作为根节点 找其子树的最大距离和父节点的最大距离 dfs1:求子树对于当前根节点的最大距离和次大距离 求次大距离原因:如果当前节点是其父节点子树的最大路径上的点,最大距离不…...
【Java基础】面向对象是什么
面向对象和面向过程的对比 类和对象 class Car{} 是描述对象(车)的类,属于引用数据类型用来描述对象具有的属性(变量)和行为(函数),属于概念模型 Car baomanew Car(); 对象需要由类来创建对象具备了类中定义的属性和行为 对象…...

家用洗地机应该怎么选?哪个牌子好?市场上主流洗地机品牌推荐
洗地机的出现,让越来越多的家庭享受清洁的过程,给人们腾出来更多的时间陪伴家人和休息。但是在选购一台洗地机前,大家多多少少肯定有些疑问,洗地机到底实不实用?好不好用?能扫干净吗?还有哪些好…...

python Django REST framework允许你根据API的版本提供不同的行为或数据
在Django REST framework中,版本控制是一个重要的功能,它允许你根据API的版本提供不同的行为或数据。以下是如何在Django REST framework中设置API版本控制的几种方法: 1. 使用URL路径参数 你可以通过URL路径中的参数来指定API的版本。例如: python复制 # urls.py from …...

unity给物体添加可以包裹所有子物体的BoxCollider
代码如下可直接调用 MeshTool.SpawnCollider(mode);using UnityEngine;public class MeshTool {public static Bounds SpawnCollider(Transform target){Vector3 pMax Vector3.zero;Vector3 pMin Vector3.zero;Vector3 center Vector3.zero;Vector3 oldPos target.transfor…...
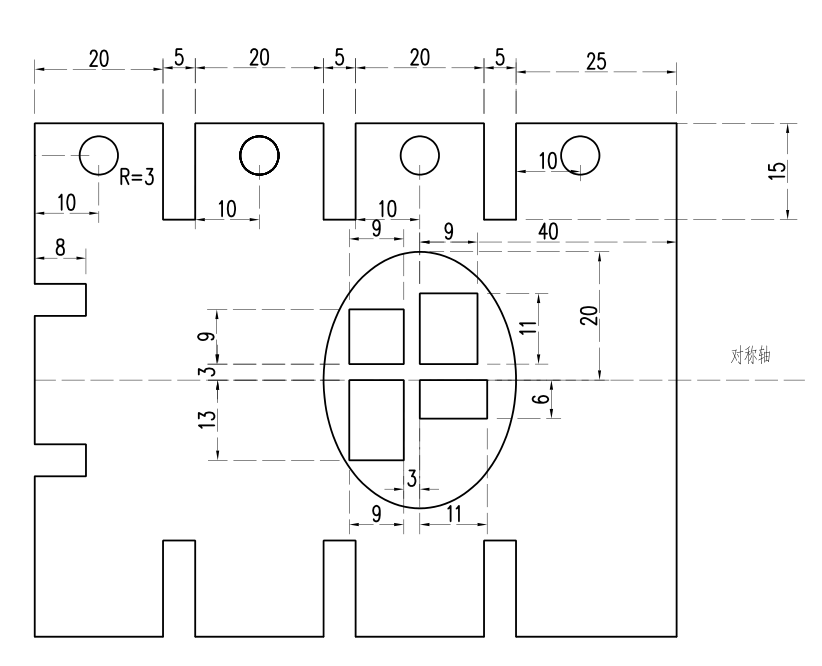
2024五一数学建模A题思路代码与论文分析
2024五一数学建模A题完整代码和成品论文获取↓↓↓↓↓ https://www.yuque.com/u42168770/qv6z0d/gyoz9ou5upvkv6nx?singleDoc# 2024五一数学建模A题钢板最优切割路径问题需要建立的模型和算法: 图论 最短路径算法(Dijkstra算法、Floyd算法等) 动态规划 网格化离散建模 …...
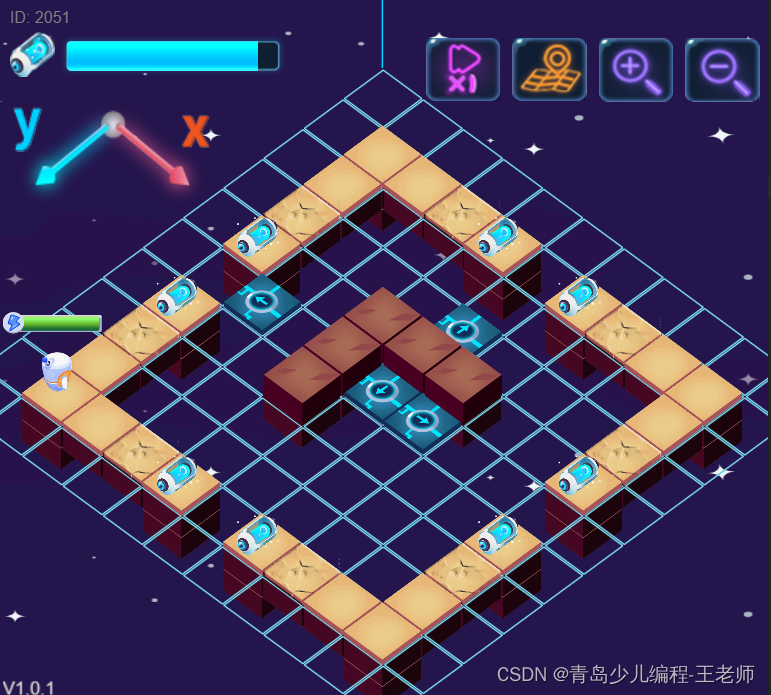
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2 1、 a 4 # 变量a存储的数字是4 Dev.step(a) # 因为变量a的值是4,所以Dev.step(a)就相当于Dev.step(4)2、 a 1 # 变量a的值为1 for i in range(4):Dev.step(a)Dev.turnLeft()a a 1 # 变量a的值变为…...

科技控必看!让你轻松成为机器人领域达人
科技控们注意了!你是不是经常对机器人技术充满无限的好奇,却又因为缺乏合适的渠道而难以深入了解和亲身体验呢?别担心,BFT机器人,正是你探索机器人世界的绝佳之地! 在这里,你将发现一个充满惊喜…...

Linux进程——Linux下常见的进程状态
前言:在进程学习这一块,我们主要学习的就是PCB这个进程控制块,而PBC就是用来描述进程的结构体,而进程状态就是PCB结构体中的一个变量。 本篇主要内容: 操作系统中的进程状态Linux下的进程状态 在开始之前,我…...

TCP长连接短链接
1、短连接 短连接是指通讯双方有数据交互时,就建立一个连接,数据发送完成后,则断开此连接,即每次连接只完成一项业务的发送。 2、长连接 长连接是指在一个连接上可以连续发送多个数据包,在连接保持期间,…...

代码随想录35期Day33-Java
Day33题目 LeetCode1005:K 次取反后最大化的数组和 核心思想:每次取反都取反最小的。如果有负数,则一直取反最小的负数,如果没有就取反正数。取反次数只需要看是奇数还是偶数。偶数则正数序列不变,奇数则最小的变成负数 class …...
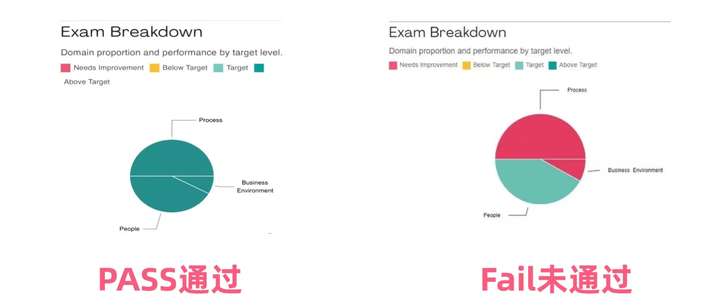
PMP考试没过怎么办?如何补考?(附复核流程)
最近刷小红书,看很多人都在晒PMP通过的成绩截图,一方面为大家开心,终于拿到了期盼已久的PMP,但同时也有宝子发挥失常没通过考试,所以这期针对没考过的宝子们,出一期复盘文章,无论结果如何&#…...
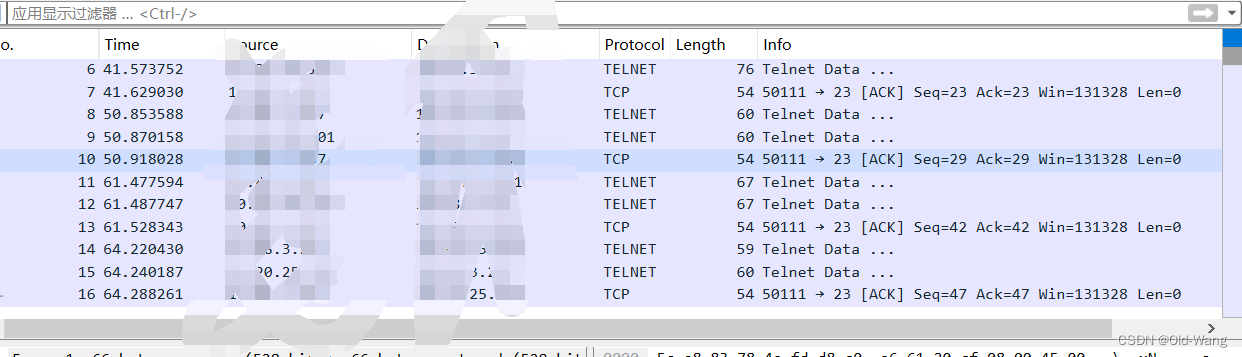
自主实现Telnet流量抓取
自主实现Telnet流量抓取 根据测试需求,需要抓取Telnet流量包,使用wireshark Python(socket、telnetlib库)实现 实现代码 主要此处有坑, 根据协议规则,wireshark 默认端口为23 的是Telnet协议࿰…...

以瓦片地图为底图添加图表,保留拖拽功能
1、问题1 在地图上覆盖一个容器层,容器层上的内容显示不出来如何解决? 原因:堆叠指数问题 解决方案:绝对定位后,提升其z-index值即可 2、问题2 在地图上覆盖一个容器层,影响了地图拖拽,如何…...

Windows cmd bat之特殊符号及变量
cmd 常用变量 bat批处理常用命令 %1~%9表示拖入文件(%0以外的输入文件),%0表示批处理文件本身 %0~%1字母意思基本相同,不区分大小写 ::打印当前窗口地址 echo “%cd%” %0 获取当前文件路径 %~d0 …...
用python写个控制MicroSIP自动拨号和定时呼叫功能(可用在小型酒店叫醒服务)
首先直接上结果吧,MicroSIP 助手,控制MicroSIP自动拨号,定时呼叫的非常实用小工具! 在使用MicroSIP 助手之前,我们需要了解MicroSIP是什么,MicroSIP是一个SIP拨号软件,支持注册任意SIP平台实现拨…...

axios 取消token 模糊搜索
import axios from ‘axios’; // 创建一个取消令牌源(cancel token source) const CancelToken axios.CancelToken; const source CancelToken.source(); // 下拉框搜索函数 function search() { // 获取输入值 const inputValue document.getElem…...

【OTS4WORD】“精简并行过程”——容易剪裁的“软件过程改进方法和规范”模板
附件资源是作者针对SPP采用模板重新格式化打包制作,原模板具有格式不受控的缺点,导致文档编制过程中引起不必要的排版麻烦。 附件资源适用于希望改进工作流程,适配CMMI质量管理体系的公司或个人使用,质量改进管理组织、项目管理组…...

22 | MySQL有哪些“饮鸩止渴”提高性能的方法?
短连接风暴 第一种方法:先处理掉那些占着连接但是不工作的线程。 kil id 第二种方法:减少连接过程的消耗。 让数据库跳过权限验证阶段,重启数据库,并使用–skip-grant-tables 参数启动。 慢查询性能问题 索引没有设计好 创建索引都支持 Online DDL 了,对于那种高峰期数…...

【AIGC调研系列】VILA-1.5版本的视频理解功能如何
VILA-1.5版本的视频理解功能表现出色,具有显著的突破。这一版本不仅增强了视频理解能力,还提供了四种不同规模的模型供用户选择,以适应不同的应用需求和计算资源限制[1][2][3]。此外,VILA-1.5支持在笔记本等边缘设备上部署&#x…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
