LeetCode-hot100题解—Day6
原题链接:力扣热题-HOT100
我把刷题的顺序调整了一下,所以可以根据题号进行参考,题号和力扣上时对应的,那么接下来就开始刷题之旅吧~
1-8题见LeetCode-hot100题解—Day1
9-16题见LeetCode-hot100题解—Day2
17-24题见LeetCode-hot100题解—Day3
25-34题见LeetCode-hot100题解—Day4
39-56题见LeetCode-hot100题解—Day5
注:需要补充的是,如果对于每题的思路不是很理解,可以点击链接查看视频讲解,是我在B站发现的一个宝藏UP主,视频讲解很清晰(UP主用的是C++),可以结合视频参考本文的java代码。
力扣hot100题解 62-71
- 62.不同路径
- 63.不同路径Ⅱ
- 64.最小路径和
- 66.加一
- 67.二进制求和
- 69.x的平方根
- 70.爬楼梯
- 71.简化路径
62.不同路径
思路:
本题采用动态规划来求解,最后需要得到的时候到达网格右下角的路径的数量,设f(i,j)是到达f[i][j]的路径数量,由于每次只能向下或者向右移动,所以可以用f(i,j)=f(i-1,j)+f(i,j-1)来计算路径数量,其中f(i-1,j)是指到f[i][j]上一格的数量,f(i,j-1)是指到达f[i][j]左边一格的路径数量,那么动态方程为f(i,j)=f(i-1,j)+f(i,j-1),最后返回f(m-1,n-1)的值即为所求,详细的视频讲解点击视频讲解-不同路径。
时间复杂度:
由于要对整个二维数组进行遍历计算,所以时间复杂度为O(mn),需要开辟一个二维数组来存储对应格子的路径数,所以空间复杂度也为O(mn)。
代码实现:
class Solution {public int uniquePaths(int m, int n) {int[][] f = new int[m][n];for(int[] item : f){Arrays.fill(item,1);}for(int i = 1; i < m; i++){for(int j = 1;j < n;j++){f[i][j] = f[i - 1][j] + f[i][j - 1];}}return f[m-1][n-1];}
}
知识点扩展:
对数组元素进行初始化设置可以使用以下函数,需要注意的是是的,Arrays.fill(nums,x)方法只能用于一维数组。该方法用指定的值填充整个数组,对于多维数组,每个维度需要分别使用fill方法进行填充。
//将nums数组的元素初始化为x
Arrays.fill(nums,x)
63.不同路径Ⅱ
思路:
本题是62题的加强版,思路基本一样,都用到了动态规划的方法,唯一不同的是本题中多了一个障碍物的限制,有障碍物的网格是不能经过的,所以我们只要加一个判断条件,如果某个网格有障碍物,则将这个网格的可到达路径设置为0即可,需要注意的是本题不能将记录路径数的二维数组初始化值为1,而应该是0,62题中第一行(i=0)和第一列(j=0)因为只能向右和向下走才能到达,所以将其初始值设置为1,在后续的遍历中就可以直接从i=1和j=1开始遍历数组,但是本题中第一行和第一列可能会出现障碍物,所以也要统一处理,遍历时也需要从0开始,同时为了保证第一行和第一列没有障碍物时可能正确的记录其可到达的路径数量,需要将其实位置的路径数置为1,视频讲解点击视频讲解-不同路径Ⅱ。
时间复杂度:
时间复杂度和空间复杂度同62题,均为O(mn)。
代码实现:
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] f = new int[m][n];for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){//判断是否有障碍物,有则直接跳过if(obstacleGrid[i][j] == 1) continue;//将f[0][0] = 1,方便对第一行和第一列的路径数的计算if(i == 0 && j == 0) f[i][j] = 1;else{//i>0时 路径数等于到达上面格子的路径数+f[i][j]if(i > 0) f[i][j] += f[i - 1][j];//j>0时 路径数等于到达左边格子的路径数+f[i][j]if(j > 0) f[i][j] += f[i][j - 1];}}}return f[m - 1][n - 1];}
}
64.最小路径和
思路:
本题采用动态规划的方法来解决,设f(i,j)表示从(0,0)到(i,j)的路径和,由于每次只能向右或者向下走,所以可以得到以下的两个动态方程:
//从上面格子向下走
f[i][j] = f[i - 1][j] + grid[i][j]
//从左边格子向右走
f[i][j] = f[i][j - 1] + grid[i][j]
要得到最小路径和,所以两种走法中取最小值即可,所以最终的动态方程为:
f[i][j] = Math.min(f[i - 1][j],f[i][j - 1]) + grid[i][j]
注意最后在代码中不要直接使用该动态方程,因为要分别处理i和j为0的情况,视频讲解点击视频讲解-最小路径和。
时间复杂度:
由于要遍历二维数组得到每一格的路径和,所以时间复杂度为O(mn),开辟一个二维数组来记录每一格的路径和,所以空间复杂度为O(mn)。
代码实现:
class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] f = new int[m][n];//初始化为最大值for(int[] item : f){Arrays.fill(item,Integer.MAX_VALUE);}for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){//(0,0)处的值为网格的值,特判处理if(i == 0 && j == 0) f[i][j] = grid[i][j];else{//处理j为0,即第一列的情况if(i > 0) f[i][j] = Math.min(f[i][j],f[i - 1][j] + grid[i][j]);//处理i为0,即第一行的情况if(j > 0) f[i][j] = Math.min(f[i][j],f[i][j - 1] + grid[i][j]);}}}return f[m - 1][n - 1];}
}
66.加一
思路:
本题需要对数组元素组成的数字进行加一操作,重点在于加法操作中对进位的处理,可以分为两种情形:
- 当数组最后一个元素小于9时,最后一个元素直接加一,然后直接返回数组即可。
- 当数组最后一个元素大于9时,需要考虑到进位,将数组最后一个元素置为0,进位+1,然后继续对倒数第二个元素进行加一处理,依次类推。这里需要对数组元素全是9做特判处理,需要在结果数组的开头插入元素1。
视频讲解点击视频讲解-加一。
时间复杂度:
这个算法的时间复杂度为O(n),其中n是输入数组digits的长度。在大多数情况下,算法只需遍历一次数组,因此时间复杂度为O(n)。但在最坏情况下,需要创建一个新的数组,并将所有元素复制到新数组中,此时时间复杂度为O(n+1),即O(n)。因此,可以将算法的时间复杂度简化为O(n)。
代码实现:
class Solution {public int[] plusOne(int[] digits) {for(int i = digits.length - 1 ;i >= 0; i--){if(digits[i] < 9){digits[i]++;break;}else{digits[i] = 0;if(i == 0){int[] newdigits = new int[digits.length + 1];newdigits[0] = 1;for(int j = 1; j < digits.length + 1 ;j++){newdigits[j] = digits[j - 1];}digits = newdigits;}}}return digits;}
}
67.二进制求和
思路:
本题直接对二进制进行求和,使用StringBuilder来构建结果字符串(关于StringBuilder的使用下面的知识拓展中做了总结,之前系列文章中也有简单介绍(LeetCode-hot100题解—Day3中 17.电话号码的字母组合),因为要动态的往结果数组里添加元素,所以不建议直接使用String),并使用carry变量来记录进位。从字符串的末尾开始,逐位相加,并将结果插入到StringBuilder的开头。代码中将a和b两个字符串中对应位置的元素全部加到carry中,最后使用carry%2得到结果,carry/2更新carry的值。视频讲解点击视频讲解-二进制求和,其中有详细的模拟演示。
时间复杂度:
该方法的时间复杂度为O(max(n,m)),其中n和m分别是字符串a和b的长度。在最坏情况下,需要遍历较长的字符串并执行常数时间操作。所以时间复杂度可以看成O(n)。
代码实现:
class Solution {public String addBinary(String a, String b) {StringBuilder ans = new StringBuilder();int carry = 0;int i = a.length() - 1;int j = b.length() - 1;while(i >= 0 || j >= 0 || carry > 0){if(i >= 0){carry += a.charAt(i) - '0';i--;} if(j >= 0){carry += b.charAt(j) - '0';j--;} ans.insert(0,carry % 2);carry /= 2;}return ans.toString();}
}
知识拓展:
以下总结了StringBuilder的一些基本用法,需要注意的是,StringBuilder是线程不安全的,如果需要在多线程环境中使用,应该考虑使用StringBuffer类。
//1.创建StringBuilder对象
//创建一个空的StringBuilder对象
StringBuilder s = new StringBuilder();
//创建一个包含初始字符串的StringBuilder对象
StringBuilder s = new StringBuilder("Hello");
//创建一个初始容量为100的StringBuilder对象
StringBuilder s = new StringBuilder(100);//2.添加字符串或字符
//添加字符串
s.append("World")
//添加空字符串
s.append(" ");
//添加一个字符
s.append('!');//3.插入字符串或字符
//在索引5处插入字符串"world"
s.insert(5,"world");
//在索引0处插入字符'!'
s.insert(0,'!');//4.删除字符或字符串
//删除索引5到10之间的字符,包括索引为5的字符,不包括索引为10的字符,左闭右开
s.delete(5,10);
//删除索引0处的字符
s.deleteCharAt(0);//5.替换字符串或字符
//替换索引5到10之间的字符为"nihao"
s.replace(5,10,"nihao");
//替换索引0处的字符为"N"
s.replace(0,1,"N");//6.获取字符串
//将StringBuilder对象转换为字符串
String str = s.toString();
69.x的平方根
思考:
由于题目不允许使用任何内置指数函数和算符,所以采用二分查找来解决该问题。首先定义左右边界,计算中点mid的平方值,如果该值小于等于x值,则说明x的平方根在mid的右侧,此时更新左边界l的值为mid(因为mid的值也可能是结果);如果该值大于x,则说明x的平方根在mid的左侧,此时更是右边界r的值为mid-1(mid的平方值大于x,所以mid肯定不是所求的结果),最后循环结束,返回l和r任意一个即为所求,视频讲解点击视频讲解-x的平方根。
时间复杂度:
使用二分查找,时间复杂度为O(logn)。
代码实现:
class Solution {public int mySqrt(int x) {int l = 0;int r = x;while(l < r){int mid = l + (r - l) / 2 + 1;if((long)mid * mid <= x) l = mid;else r = mid - 1; }return l;}
}
70.爬楼梯
思路:
本题采用动态规划来解决,假设f(i)表示爬到i阶的方法数,那么f(1) = 1,第1阶爬1阶到达,有一种方法,f(2)=2,第2阶可以可以从1阶爬到2阶,也可以直接爬2阶到2,所以有两种方法;由于一次可以爬1阶或2阶,所以动态方程为f(i)=f(i-1)+f(i-2),其中f(i-1)表示爬到i-1阶的方法数,爬到i需要爬1阶,可以到达i阶,f(i-2)表示爬到i-2阶的方法数,爬到i阶需要爬2阶,可以到达i阶,两者加起来即为爬到i阶的方法数,视频讲解点击视频讲解-爬楼梯。
时间复杂度:
时间复杂度为O(n),由于开辟了一个数组来保存爬到每一阶的方法数,空间复杂度为O(n)。
代码实现:
class Solution {public int climbStairs(int n) {//数组大小设置为n+2,防止溢出int[] f = new int[n + 2];f[1] = 1;f[2] = 2;for(int i = 3;i <= n;i++){f[i] = f[i - 1] + f[i - 2];}return f[n];}
}
71.简化路径
思路:
根据题意可知,当在路径中遇到"."时表明当前目录,不做处理;当在路径中遇到".."时表明上级目录,需要返回上级目录,所以可以将path中的目录全部压入栈中,当遇到".."时,弹出栈顶元素(即回到上一级目录),最后在遍历完path后将栈中的元素逆序拼接输出即可,如果栈为空,直接返回根目录"/",视频讲解点击视频讲解-简化路径。关于java中Stack的使用在之前系列文章(LeetCode-hot100题解—Day3 20.有效的括号)中总结过,如果需要可以去复习一下。
时间复杂度:
时间复杂度是O(n),其中n是路径字符串path的长度,只对path进行了一次遍历。
代码实现:
class Solution {public String simplifyPath(String path) {Stack<String> stk = new Stack<>();String[] items = path.split("/");for(String item : items){if(item.equals("..")){if(!stk.isEmpty()){stk.pop();}}else if(!item.equals(".") && !item.equals("")){stk.push(item);}}StringBuilder ans = new StringBuilder();while(!stk.isEmpty()){ans.insert(0,"/"+stk.pop());}//如果栈为空,直接返回根目录"/"return ans.length() == 0 ? "/" : ans.toString();}
}
知识拓展:
equals和==的使用
使用"=="运算符判断两个对象是否相等时,它实际上比较的是两个对象的引用地址,而不是它们的值,也就是说,它检查的是两个对象是否指向相同的内存位置。
而使用equals()方法可以比较两个对象的值是否相等,equals() 不能用于判断基本数据类型的变量,只能用来判断两个对象是否相等。在Java中,equals()方法是Object类的方法,所有的类都继承了它。默认情况下,equals()方法与"=="运算符的行为相同,比较的是两个对象的引用地址。
但是,很多类会覆盖equals()方法,以便根据对象的内容来判断它们是否相等。例如,在字符串类(String)中,String 中的 equals 方法是被重写过的,equals()方法比较的是字符串的内容(也就是对象的值),而不是引用地址。
因此,如果你想比较两个对象的值是否相等,应该使用equals()方法,而不是"=="运算符。
相关文章:

LeetCode-hot100题解—Day6
原题链接:力扣热题-HOT100 我把刷题的顺序调整了一下,所以可以根据题号进行参考,题号和力扣上时对应的,那么接下来就开始刷题之旅吧~ 1-8题见LeetCode-hot100题解—Day1 9-16题见LeetCode-hot100题解—Day2 17-24题见LeetCode-hot…...

【Linux】gcc/g++的使用
🎉博主首页: 有趣的中国人 🎉专栏首页: Linux 🎉其它专栏: C初阶 | C进阶 | 初阶数据结构 小伙伴们大家好,本片文章将会讲解Linux中gcc/g使用的相关内容。 如果看到最后您觉得这篇文章写得不错…...
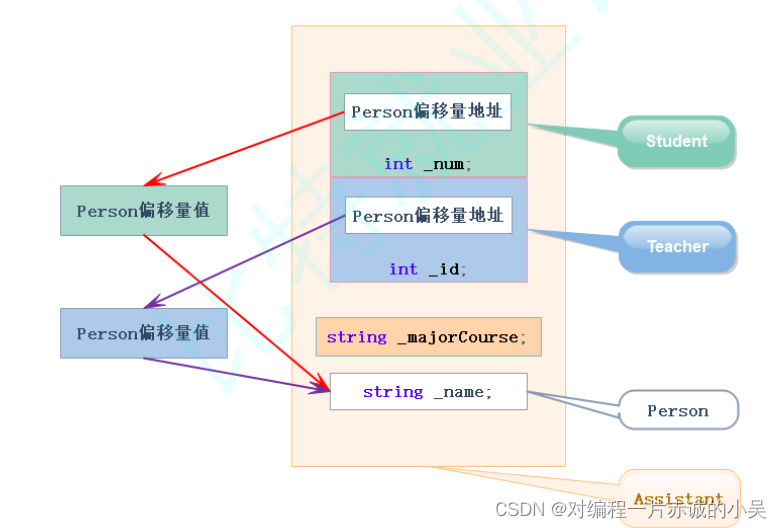
2024-5-3学习笔记 虚拟继承原理
目录 原理 总结 前面提到过,解决菱形继承产生的数据二义性问题和数据冗余,就需要用到虚拟继承,关于它是如何解决的,我们来一起研究。 class Person { public :string _name ; // 姓名 }; class Student : virtual public Perso…...

C语言什么是“野指针”?
一、问题 “野指针”是⼀个⽐较陌⽣的术语,那么它到底是什么呢? 二、解答 当程序⾥声明了⼀个指针⽽又没有给这个指针赋值,使其指向⼀个地址时,这样的指针就称为“野指针”。 “野指针”会随意地指向⼀个地址。当对这个指针进⾏操…...
LeetCode--所有质数、质数对
1.0 Q: 输出 100 以内所有质数 1.1 /* 第一层循环控制检查到哪个数* 第二层通过遍历除以每个比他小的数的方式,检查每个数是不是质数* 由于要遍历检查,设置一个标记,只要任意一次循环可以整除,我们就设置该标记为不是质数 */boolean isPrime true;for (int i 2; i < 100…...
JavaScript异步编程——05-回调函数
我们在前面的文章《JavaScript 基础:异步编程/单线程和异步》中讲过,Javascript 是⼀⻔单线程语⾔。早期我们解决异步场景时,⼤部分情况都是通过回调函数来进⾏。 (如果你还不了解单线程和异步的概念,可以先去回顾上一…...
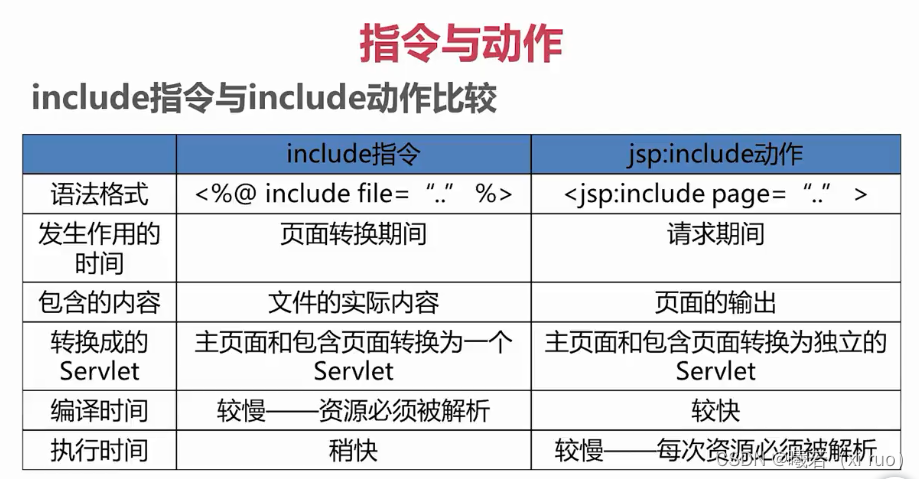
JAVA基础之jsp标准标签
jsp动作标签实现实例化一个实体类 <jsp:useBean id"标识符" class"java类名" scope"作用范围"> 传统的java方式实例化一个实体类 Users user new Users(); <%%> id: 对象名 * class:类 创建对象时,完全限定名(包名…...

VM16激活码以及连接centos7过慢的问题
一、激活码 任选一个,直到能用为止 ZF3R0-FHED2-M80TY-8QYGC-NPKYF YF390-0HF8P-M81RQ-2DXQE-M2UT6 ZF71R-DMX85-08DQY-8YMNC-PPHV8 FA1M0-89YE3-081TQ-AFNX9-NKUC0 二-连接centos7过慢的问题 先备份/etc/ssh/sshd_config,备份命令为 cp /etc/ssh/sshd_config /etc/…...

MySQL 迁移到 Oracle 需要注意的问题
MySQL /Oracle 常见问题 1. VARCHAR/VARCHAR2/NVARCHAR 差异: MySQL 的 VARCHAR 是以字符为单位计算的,Oracle 的 VARCHAR 是 以字节为单位计算的,所以对中文的存储 Oracle 是 MySQL 的 2 倍 (GBK)和 3 倍(UTF8) 2. NULL 差异 A. MySQL…...
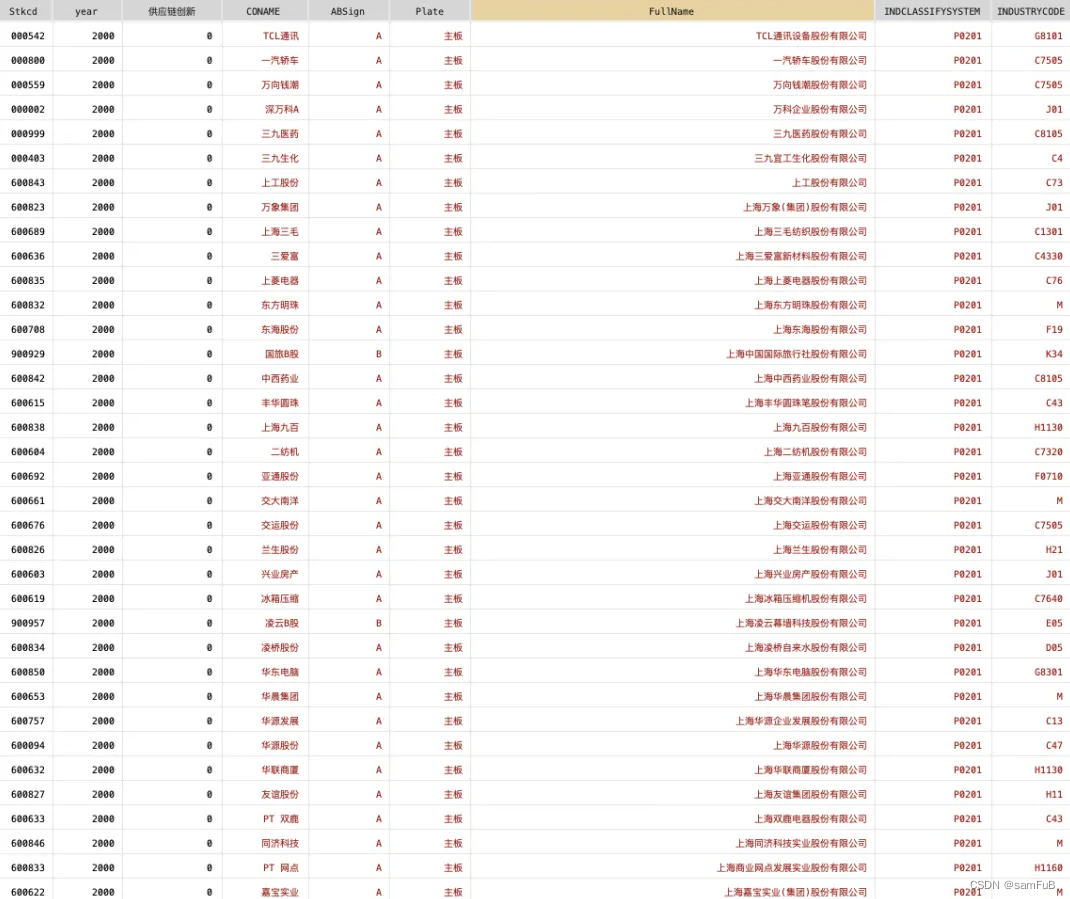
【数字经济】上市公司供应链数字化数据(2000-2022)
数据来源: 时间跨度:2000-2022年 数据范围:各上市企业 数据指标: 样例数据: 参考文献:[1]刘海建,胡化广,张树山,等.供应链数字化的绿色创新效应[J].财经研究,2023,49(03):4-18. 下载链接:https:…...

通过AOP实现项目中业务服务降级功能
最近项目中需要增强系统的可靠性,比如某远程服务宕机或者网络抖动引起服务不可用,需要从本地或者其它地方获取业务数据,保证业务的连续稳定性等等。这里简单记录下业务实现,主要我们项目中调用远程接口失败时,需要从本…...

LeetCode:盛最多水的容器
文章收录于LeetCode专栏 盛最多水的容器 给你n个非负整数a1,a2,…,an,每个数代表坐标中的一个点(i, ai) 。在坐标内画 n 条垂直线,垂直线i的两个端点分别为(i, ai) 和 (i, 0)。找出其中的两条线,使得它们与…...

阿里云 OSS桶对象存储攻防
目录 Bucket权限配置错误-公开访问 Bucket桶爆破 特定的Bucket策略配置 Bucket Object遍历...
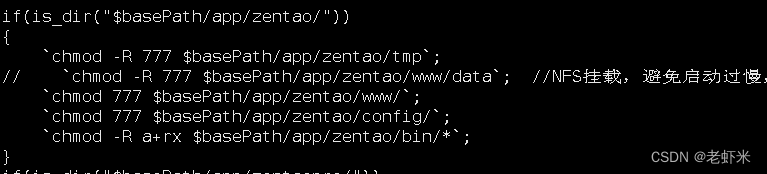
外网禅道配置
exportfs -avrf 修改代码,避免启动太慢:vi /opt/zbox/bin/zbox.php 启动和停止 /opt/zbox/zbox start /opt/zbox/zbox stop...
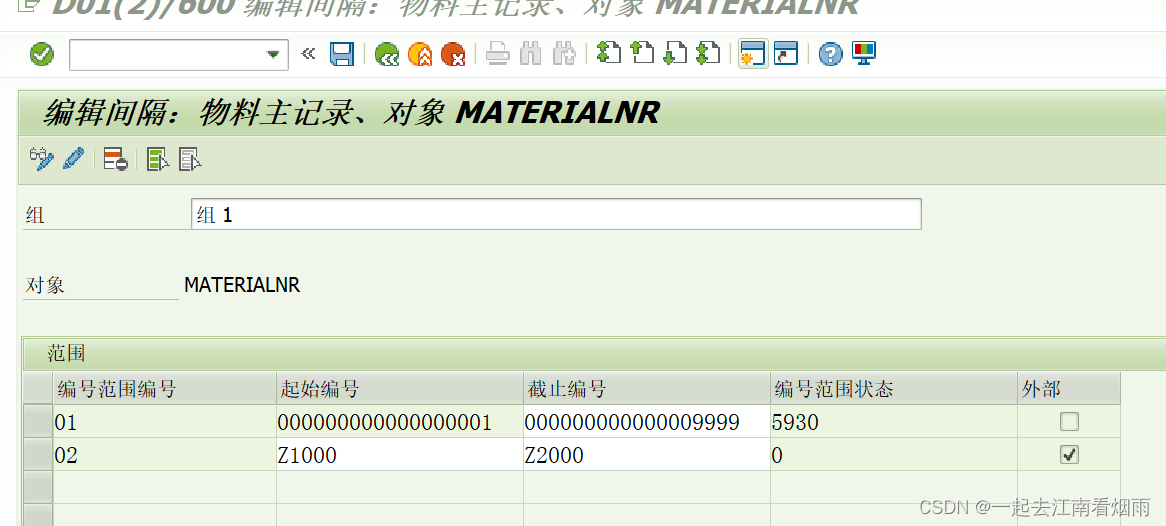
MM模块学习一(供应商创建,物料类型的定义及功能)
物料管理流程: 源头:采购需求->采购申请 MRP:物料需求计划。运行物料需求计划的结果,根据物料的性质来判断是外购(采购申请)或者是生产(计划订单->生产订单)。 采购申请&am…...
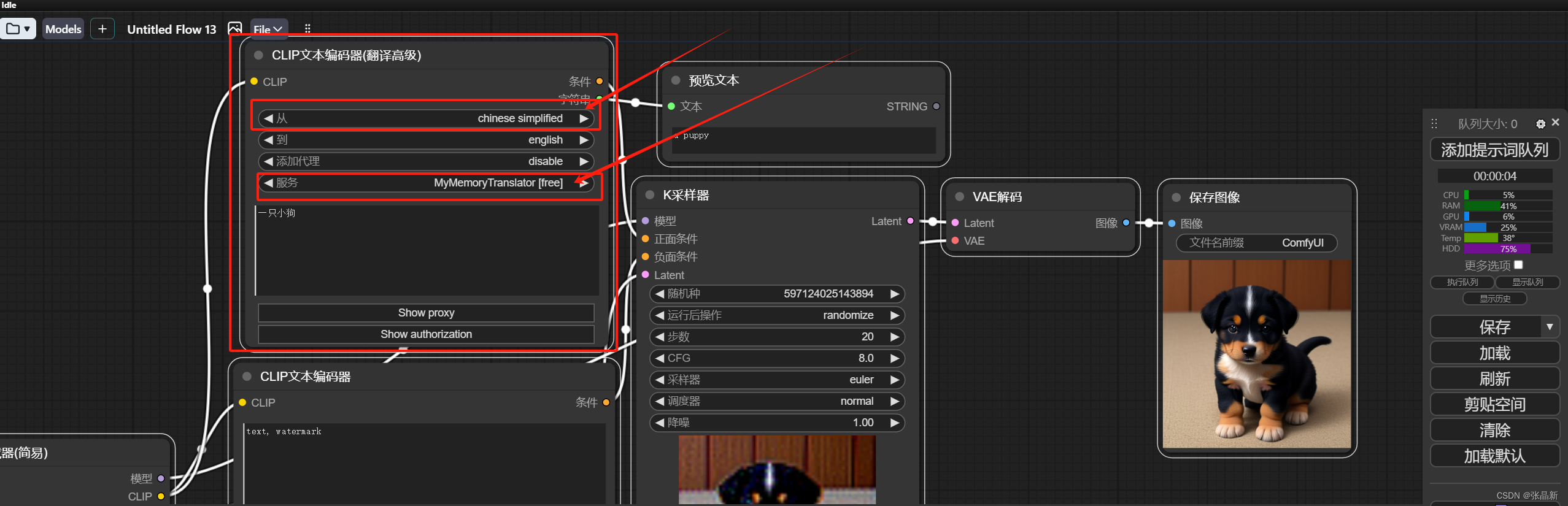
玩comfyui踩过的坑之使用ComfyUI_Custom_NODES_ALEKPET翻译组件问题
环境: 秋叶安装包,安装ComfyUI_Custom_NODES_ALEKPET组件或者直接下载网盘中的包,直接解压包到comfyui根目录/custom_nodes/,重启后,按指导文件操作。 注意:网盘指导包中有配置好的流程json文件࿰…...
偏特化Partial Specialization)
(类)偏特化Partial Specialization
当编写一个模板特化,涉及部分但不是全部模板参数时,它被称为偏特化(Partial Specialization)。【注意,偏特化是针对类模板而言,函数模板不可偏特化,只能全特化】 偏特化是C模板编程中的一种技术…...

TypeScript 基础学习笔记:interface 与 type 的异同
🔥 个人主页:空白诗 文章目录 TypeScript 学习笔记:interface 与 type 的异同🎣 引言🚀 快速入门1️⃣ Interface(接口)📋 定义🤝 实现💡 特点 2️⃣ Type Al…...
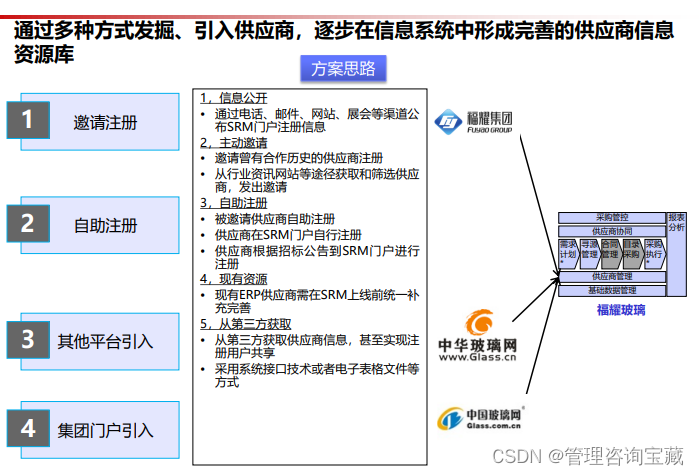
【管理咨询宝藏95】SRM采购平台建设内部培训方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏95】SRM采购平台建设内部培训方案 【格式】PDF版本 【关键词】SRM采购、制造型企业转型、数字化转型 【核心观点】 - 重点是建设一个适应战略采…...

第七届机电、机器人与自动化国际会议(ICMRA 2024)即将召开!
第七届机电、机器人与自动化国际会议(ICMRA 2024)将于2024年9月20日-22日在中国武汉举行。ICMRA 2024为各国专家学者提供一个学术交流的平台,讨论机电、机器人和自动化领域的最新研究成果和未来的研究方向,旨在能够建立起国家间&a…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
