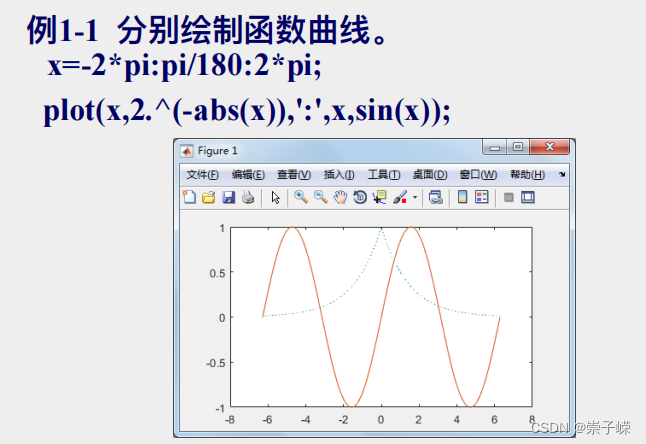
matlab例题大全
1.第1章 MATLAB系统环境
1.1
注:plot函数为画图函数。例plot(x1,y1,':',x2,y2,'*');
1.2

注:root为求根函数。p为方程变量前面系数矩阵。
1.3

注:
2*x+3y-1*z = 2;
8*x+2*y+3*z = 4;
45*x+3*y+9*z = 23
求:x,y,z的值
注:inv为求逆函数。
1.4

注:@(x)是匿名函数,这个x是可以被使用的,理解如下:
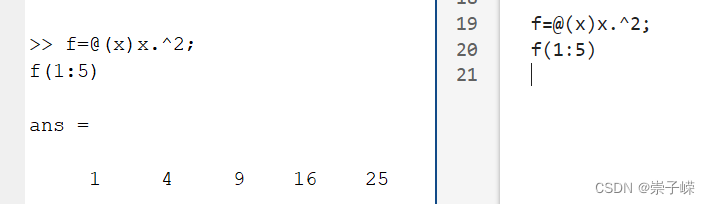
2.第2章 MATLAB数据及其运算
2.1

2.2

注:rem(A,3)的结果如果为0,返回1,负责返回0。
2.3


注:字符串可以像数组一样被应用。由于ch(k)=ch(k)-('a'-'A')结果为对应的ascci码值,所以后面要使用char函数,变回字符串。如下

3. 第3章 MATLAB矩阵分析与处理
3.1


注:magic(a),生成大大小为a*a的矩阵,并且行和列之和一样。

3.2


注:


D*A,由线性代数知识可知,D的第一行乘以A的第一列放在第一个,依此类推。
3.3

注:(1)b=[5,-2,6]‘,是行向量的转置变成列向量。
(2)inv函数为取逆函数。
补充:
(1)det函数为求矩阵行列式。
(2)rank函数为求矩阵的秩。
(3)trace函数为求矩阵的迹。
(4)norm函数为求矩阵范数。
(4)eig函数求矩阵的特征向量和特征值。
4.第4章 MATLAB程序流程控制
4.1

法一:使用脚本

法二:使用函数(调用函数时,用使用函数文件名)

4.2


注:使用input函数输入a,b,c的值,使用求根公式(-b+sqrt(b^2-4*a*C))/(2*a)求出根。
4.3
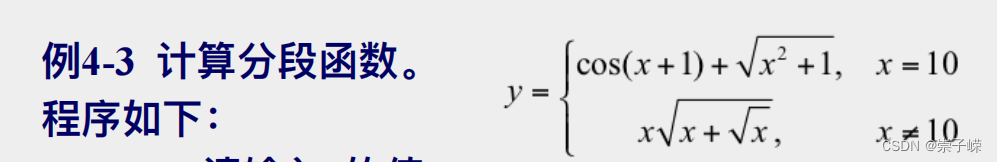

4.4

注:可以将所有的setstr换成char,一样的效果。
4.5
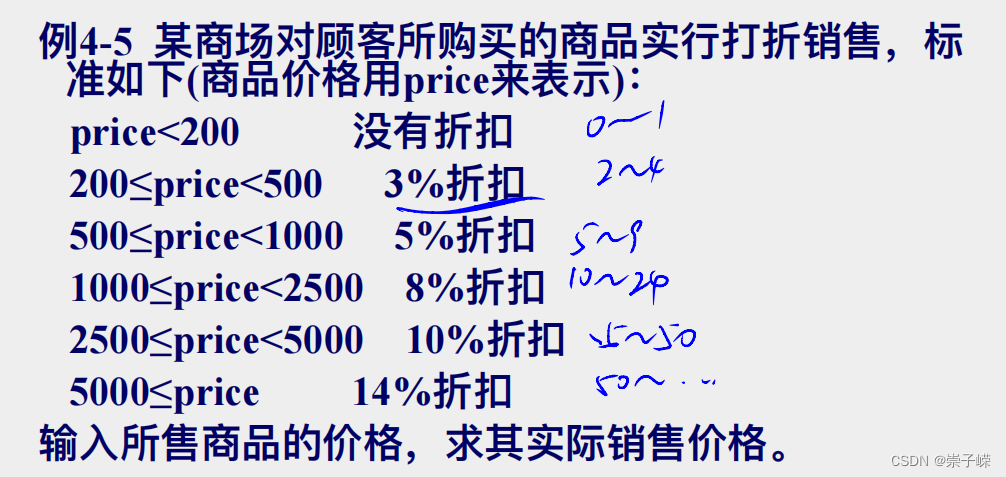

注:在switch case语句中,如果case的值同时为多个时,使用元胞数组{}。
4.6


注:fix为取整函数,rem为取余函数。
4.7
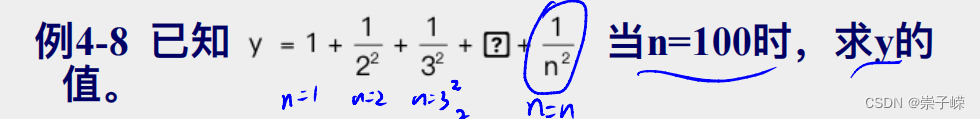
法1:

法2:

注:将1~n放在一个变量里面变成行向量,同时对这个行向量进行操作。
4.8


注:将整块面积分割成若干个小矩形。
4.9 *


注:a为4*3的矩阵,k=a,k一次取一列,所以一共取3次。
4.10


注:变量sum为所以数之和,sum/n是平均数。
4.11


注:
(1)continue为跳过一次循环中的其他语句,进行下一次循环。
(2)break为跳出整个循环。
4.12


4.13

注:nargin为函数输入时的变量个数。
5.第5章 MATLAB绘图
5.1


注:


5.2


5.3

5.4

5.5


5.6


注:plotyy函数可以将不同的量纲的函数放在统一坐标下。
5.7
![]()



5.8


注:subplot函数对窗口进行分割。
补充:
(1)

(2)

(3)

(4)

注;选项为stacked或grouped
(5)

5.9


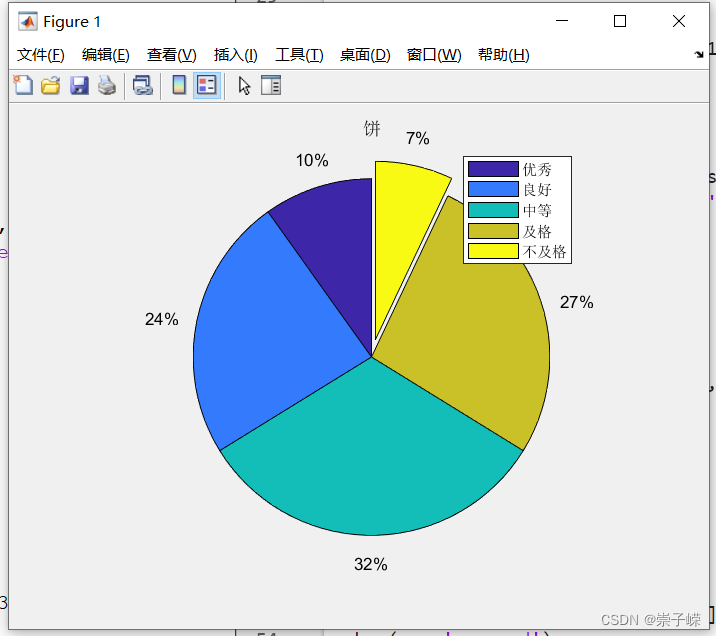
注:给1为突出,给0为不突出
5.10

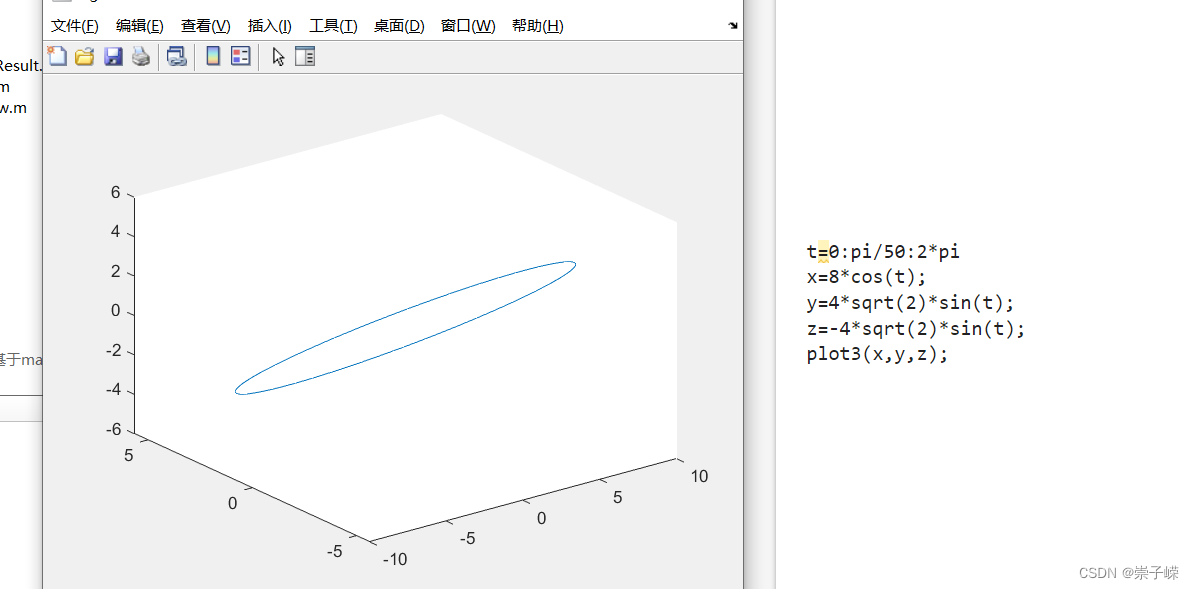
5.11


注:meshgrid画网格线
5.12


5.13
![]()

5.14
![]()

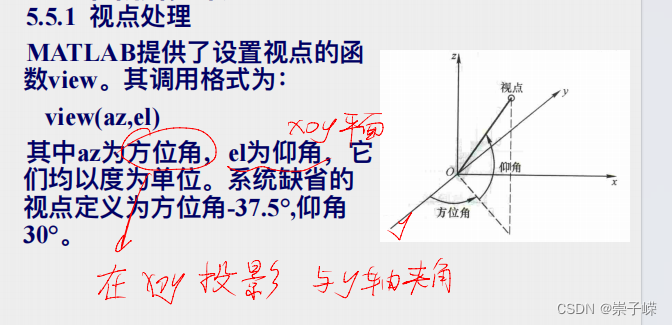
6.第6章 MATLAB数据分析与多项式计算
6.1


注:max函数为求最大值函数。max(a)求每一列的最大值,max(a,[],2)求每一行的最大值。
6.2


6.3


注:
(1)sum为求和函数,sum(a,1)为按列求和。sum(a,2)为按行求和。
(2)prod函数为求乘函数,用法与sum一样。
(3)mean函数为求平均值函数,用法与sum一样。
(4)cumsum函数为累加和函数,用法与sum一样。
(5)cumprod函数为累积和函数,用法和sum一样。
6.4
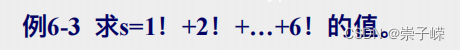

6.5


注
6.6

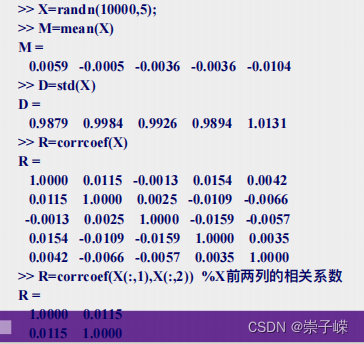
注:corrcoef函数为求相关系数函数,
6.7


注:sort为排序函数
6.8
![]()

注:多项式加法时,前一项最高次和后一项最高次不同时,较低的需要将高次补0直到与前一项最高次相同,以便于计算。
6.9


注:conv函数用于求多项式之间的乘积。
6.10


注:deconv函数用于多项式之间的除法。
6.11


注:polyder函数用于多项式的求导。
6.12


注:polyval为代数多项式函数,求指定的x时的y值
补充:polyvalm函数为求代数矩阵多项式。与polyval不同的是:

6.13


注:
(1)roots为求多项式根函数
(2)roots求出来的值,带入poly函数可以求出原函数。

6.14


对比:结果与原函数差一个系数3。
6.15

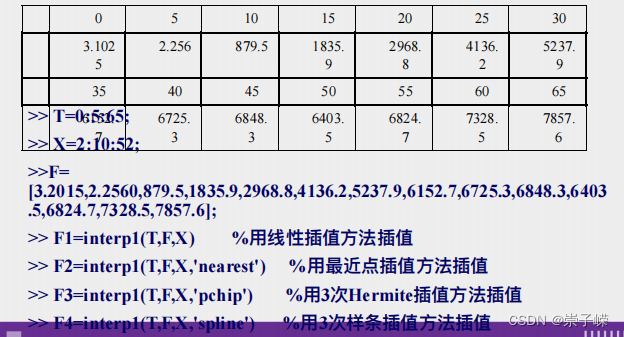
注:interp1为一维插值函数。
其中,X,Y为需要被插值函数的x和y,X1是你需要插值的点,method为你选择的插值方式:

补充:interp2为二维插值函数,其插值模式与interp2一样。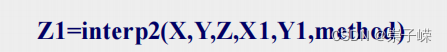
6.16


注:在指定点处插值
(1)interp2(x,y,Z,0.5,0.5),在(0.5,0.5)处插值
(2)interp2(x,y,Z,[0.5,0.6],0.4),在(0.5,0.4)和(0.6,0.4)处插值
(3)interp2(x,y,Z,[0.5,0.6],[0.4,0.5]),在(0.5,0.4)和(0.6,0.5)处插值
(4)interp2(x,y,Z,[0.5,0.6]’,[0.4,0.5]),在(0.5,0.4)和(0.5,0.5)和(0.6,0.5)和(0.6,0.4)处插值。
找规律,当为两个大小相同的行向量时,一个行向量的x仅仅与另一个行向量的y值对应。当一个为行向量一个为列向量时,一个行向量的x值与另一个列向量的所有y对应。
6.17*
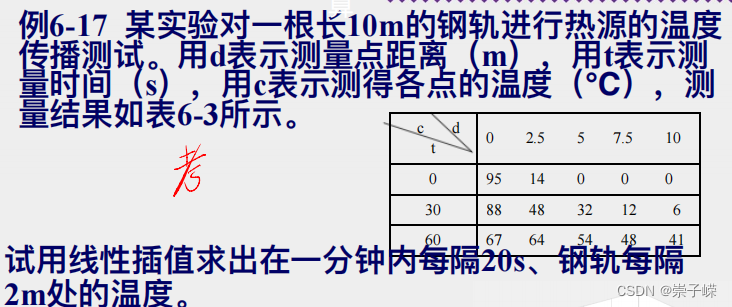

注:这个的t和ti都为列向量都是因为需要编制二维模型,只有一个为u行向量一个为列向量时才可以实现,所以要取反。
6.18


注:
(1)linspace(0,2*pi,50)等价于 0:50/pi:2*pi,用于创建数据
(2)polyfit为拟合函数,用于通过已知条件来预测给定点的值。
相关文章:

matlab例题大全
1.第1章 MATLAB系统环境 1.1 注:plot函数为画图函数。例plot(x1,y1,:,x2,y2,*); 1.2 注:root为求根函数。p为方程变量前面系数矩阵。 1.3 注: 2*x3y-1*z 2; 8*x2*y3*z 4; 45*x3*y9*z 23 求:x,y,z的…...
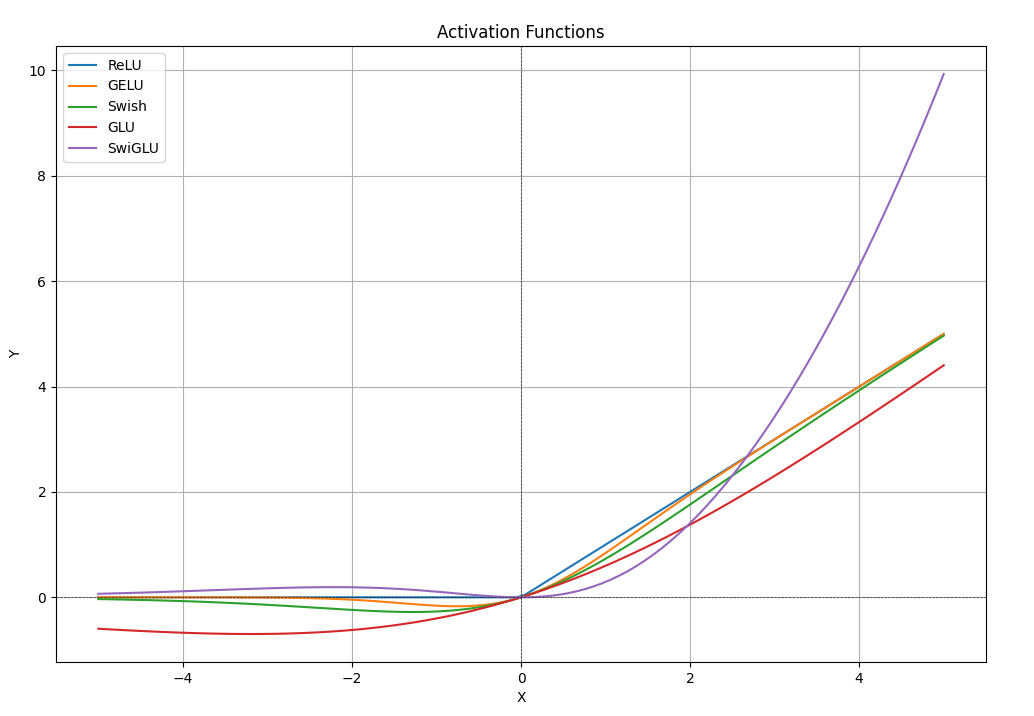
SwiGLU激活函数
SwiGLU激活函数已经成为LLM的标配了。它是GLU的变体,公式如下: SwiGLU ( x , W , V , b , c , β ) Swish β ( x W b ) ⊗ ( x V c ) \operatorname{SwiGLU}(x, W, V, b, c, \beta)\operatorname{Swish}_\beta(x Wb) \otimes(x Vc) SwiGLU(x,…...

MySQL慢查询优化
当需要优化MySQL的慢查询时,通常需要结合多个方面进行分析和优化,包括索引优化、SQL语句重构、数据库结构调整等。下面,我将通过一个例子来说明如何优化MySQL的慢查询,包括多表关联和条件查询。 假设我们有一个简化的电子商务系统…...
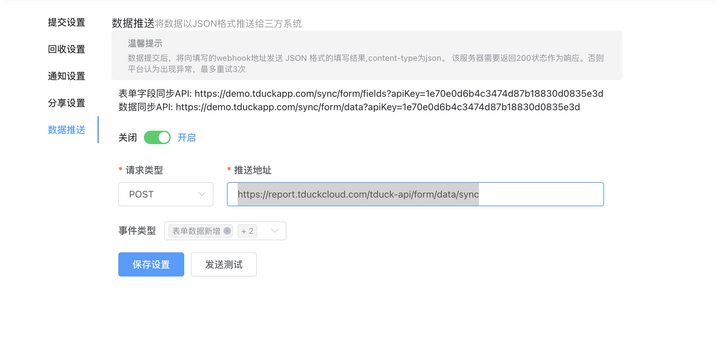
开源数据可视化大屏对接表单数据实践!
如果你需要一个表单系统,进行数据收集;可以使用tduck填鸭进行私有化部署,进行表单制作,完成数据收集。 在实际业务中,往往需要将收集的数据进行展示或分析;此时就可以使用表单数据推送到TReport中…...
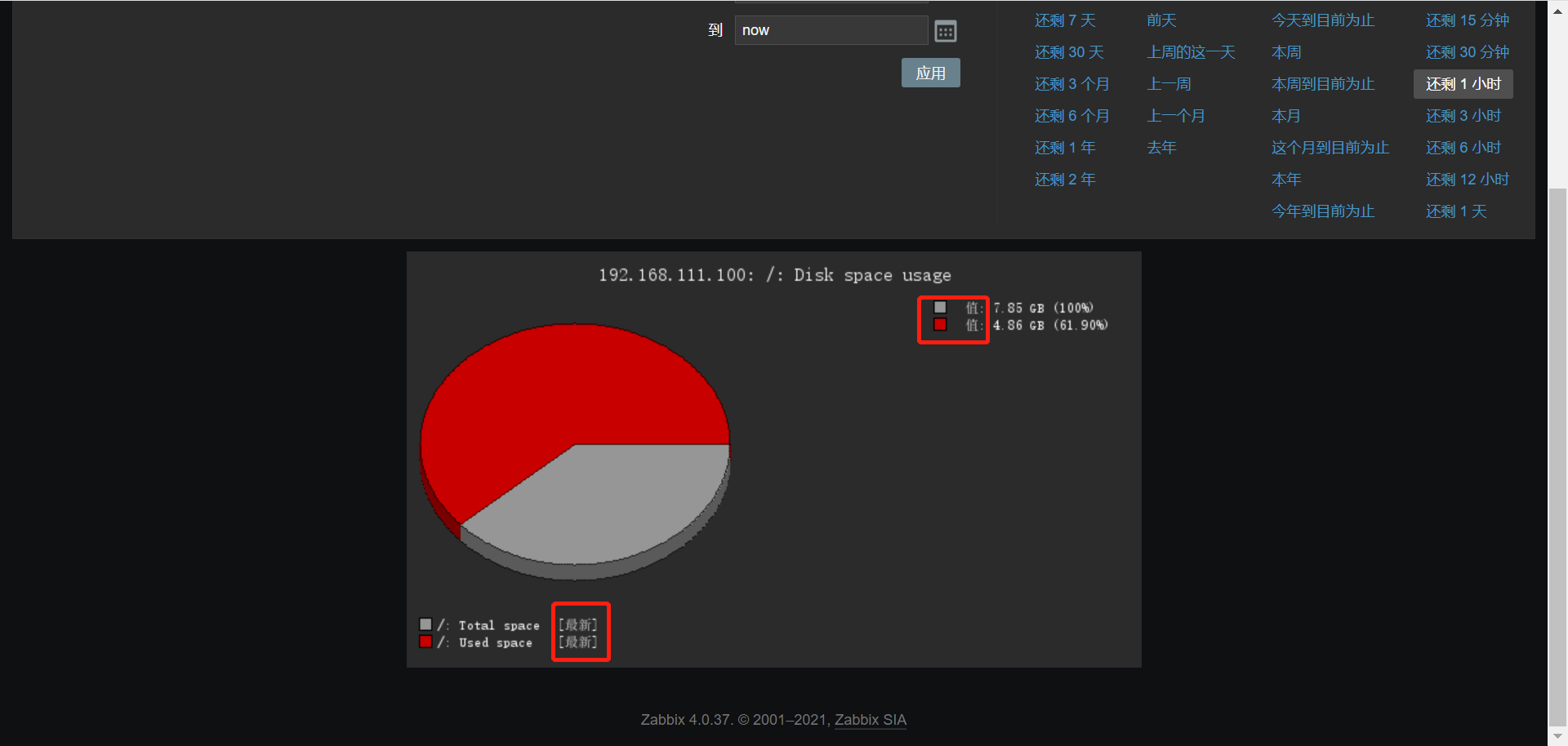
08.图形化界面字体问题处理
图形化界面字体问题处理 发现图形存在乱码,不显示文字 zabbix服务器的字符集所在的路径下: /usr/share/zabbix/assets/fonts 将本地windows系统的字体进行上传,选择一个自己喜欢的字体 上传到系统路径下并且直接覆盖掉 回到web浏览器界面…...

【代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II】
代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II 一、977.有序数组的平方 解题代码C: class Solution { public:vector<int> sortedSquares(vector<int>& nums) {int len nums.size();fo…...
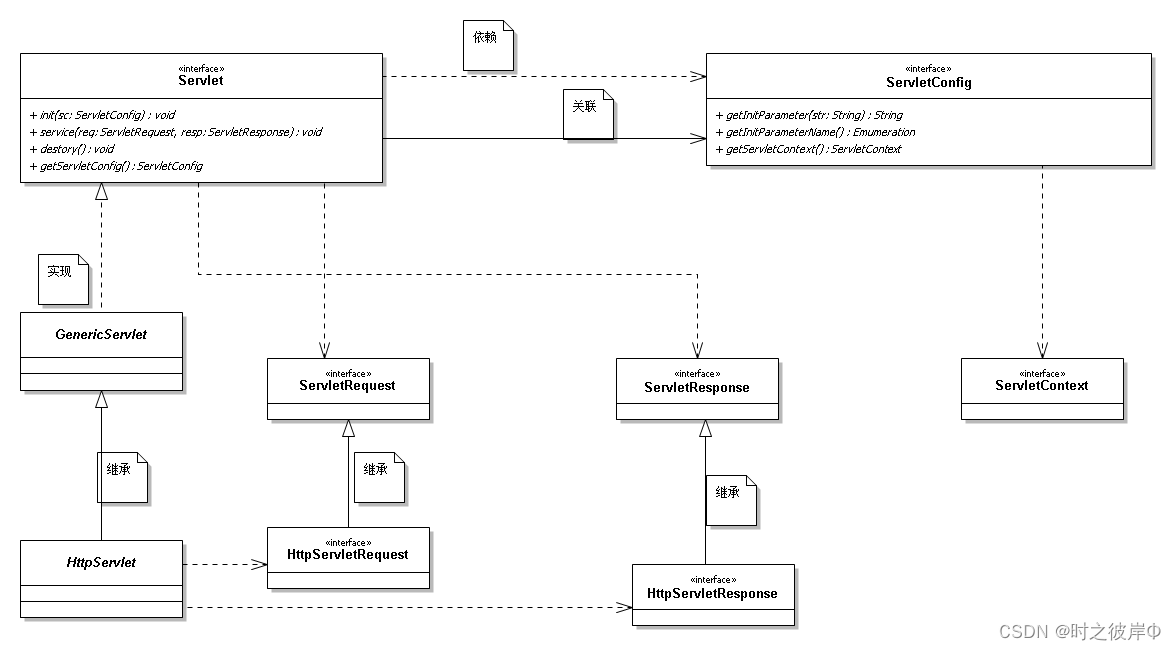
Java:Servlet详解
目录 一、什么是Servlet 二、Servlet原理 Servlet的生命周期 三、 Servlet注释 WebServlet 一、什么是Servlet Servlet是JavaWeb开发的一种技术,Servlet程序需要部署在Servlet容器(服务端)中才能运行,常见的Servlet容器有Tom…...

Oracle存储过程怎么定义类并继承
在Oracle数据库中,存储过程(Stored Procedure)是用于执行特定功能的预编译的SQL代码块。然而,Oracle的存储过程并不直接支持面向对象的编程概念,如类(Class)和继承(Inheritance&…...
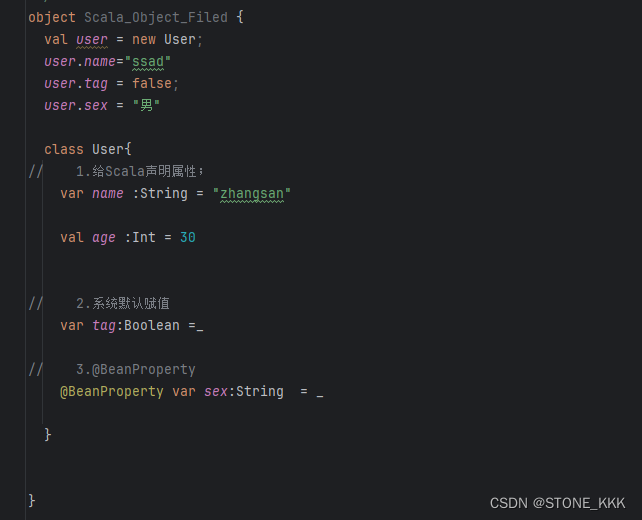
14_Scala面向对象编程_属性
文章目录 属性1.类中属性声明2.系统默认赋值3.BeanProperty4.整体代码如下 属性 1.类中属性声明 // 1.给Scala声明属性;var name :String "zhangsan"val age :Int 302.系统默认赋值 scala由于初始化变量必须赋值,为了解决此问题可以采…...

什么是网页反作弊
在搜索引擎技术中,网页反作弊是指一种防止网页排名被恶意操纵的技术。搜索引擎会根据特定的算法来评估网页的相关性和质量,以决定其在搜索结果中的排名。然而,有些人可能会尝试通过各种不正当的手段来提高自己网页的排名,这被称为…...

MAVEN打包JAR启动执行manifest
当您使用Maven进行项目打包,特别是需要创建一个可执行的JAR文件时,确保JAR文件的MANIFEST.MF中包含正确的Main-Class属性是非常重要的。这个属性告诉Java运行时环境哪个类包含main方法,作为应用程序的入口点。 如果您发现生成的JAR文件不包含…...
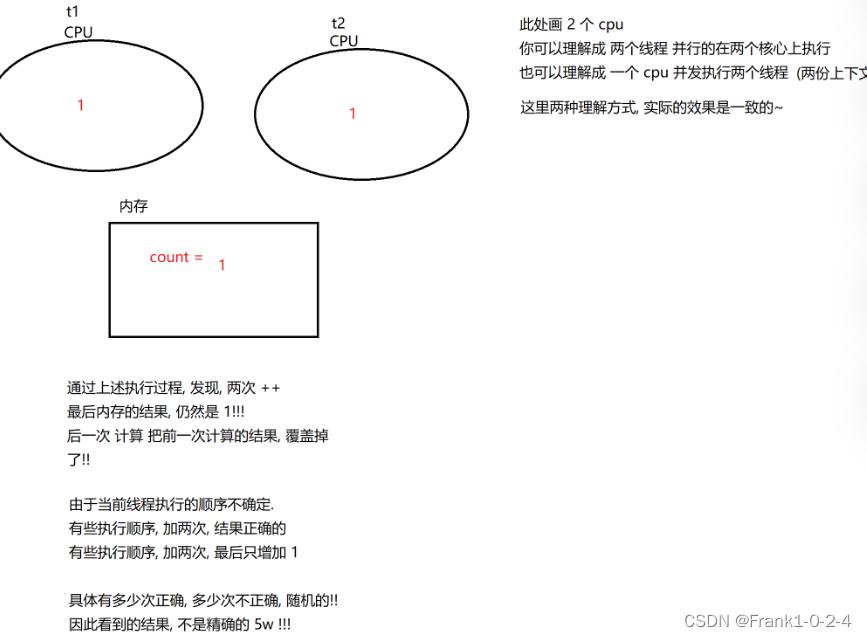
JavaEE 多线程详细讲解(1)
1.线程是什么 (shift F6)改类名 1.1.并发编程是什么 (1)当前的CPU,都是多核心CPU (2)需要一些特定的编程技巧,把要完成的仍无,拆解成多个部分,并且分别让…...
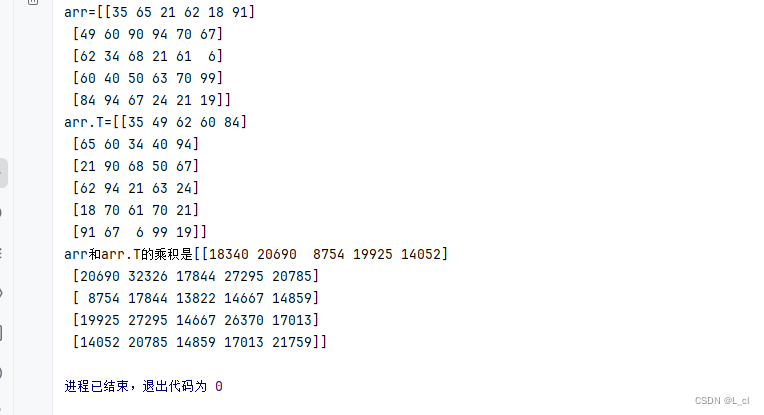
数据分析从入门到精通 1.numpy剑客修炼
会在某一瞬间突然明白,有些牢笼是自己给自己的 —— 24.5.5 一、数据分析秘笈介绍 1.什么是数据分析 是把隐藏在一些看似杂乱无章的数据背后的信息提炼出来,总结出所研究对象的内在规律。使得数据的价值最大化 案例: 分析用户的消…...

【iOS】KVO
文章目录 前言一、KVO使用1.基本使用2.context使用3.移除KVO通知的必要性4.KVO观察可变数组 二、代码调试探索1.KVO对属性观察2.中间类3.中间类的方法3.dealloc中移除观察者后,isa指向是谁,以及中间类是否会销毁?总结 三、KVO本质GNUStep窥探…...

python json字符串怎么用format方法填充参数值报KeyError
python json字符串怎么用format方法填充参数值报KeyError 需求问题分析解决方案 需求 因为python中的字典和json中的一些变量有差异,比如:json中有null、true,在python中就不会被识别,只能转换成字符串,在通过loads()…...

C++新手村指南:入门基础
目录 C概念 C发展史 C关键字(C98) 命名空间 命名空间的定义 命名空间的使用 C中的输入&&输出 缺省参数 缺省参数的概念 缺省参数的分类 函数重载 函数重载概念 函数重载实现 引用 引用的概念 引用的特性 常引用 引用的使用场景…...

智慧旅游推动旅游服务智慧化转型:借助智能科技的力量,实现旅游资源的精准匹配和高效利用,为游客提供更加便捷、舒适的旅游环境
目录 一、引言 二、智慧旅游的定义与特点 (一)智慧旅游的定义 (二)智慧旅游的特点 三、智能科技在旅游服务中的应用 (一)大数据分析助力旅游决策 (二)人工智能实现个性化推荐…...

Hikyuu-PF-银行股轮动交易策略实现
今天,带来的是“如何使用 Hikyuu 中的投资组合来实现银行股轮动交易策略”。 这个策略的逻辑很简单:持续持有两支市净率最低银行股,然后每月换仓 定义回测周期与回测标的 同样,首先定义回测周期: # 定义回测日期 …...
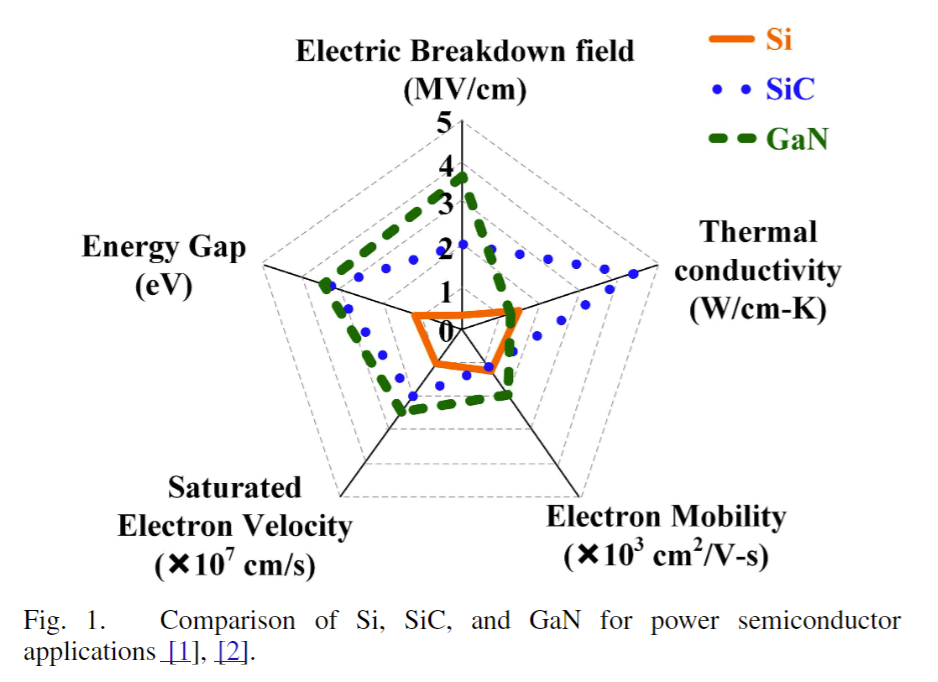
【氮化镓】GaN功率器件在转换器设计中的挑战
I. 引言(INTRODUCTION) 宽带隙(WBG)器件的重要性: 引言部分首先强调了宽带隙(WBG)器件在高频、高效率电力电子技术中的关键作用。这些器件,包括碳化硅(SiC)和氮化镓(GaN),相较于传统的硅功率器件,具有显著的优势。宽带隙半导体材料的高击穿场强允许设计更薄的漂…...
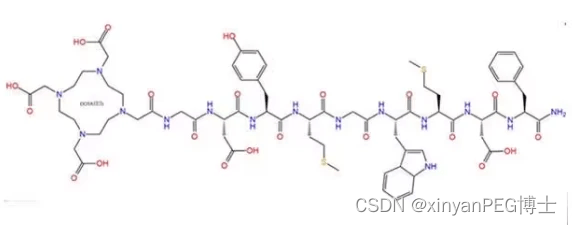
DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2,1306310-00-8,是一种重要的多肽化合物
一、试剂信息 名称:DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2CAS号:1306310-00-8结构式: 二、试剂内容 DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2是一种重要的多肽化合物,其CAS号为1306310-00-8。该多肽包含一个DO…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...