MATLAB的快速入门
第一部分:基础知识
常用命令:
clc %清除命令行窗口
clear %清空工作区数据
cd %显示或改变工作目录
clf %清除图形窗口
help %打开帮助文档
save %保存内存变量到指定文件
hold %保持图形
close %关闭当前图窗
quit %退出变量:
变量名必须以字母开头,之 后可以是任意的字母、数字或 下划线;
变量名区分字母的大小写;
变量名不超过31个字符。
常量:
ans %默认变量
pi %圆周率
inf %无穷大
exp(1) %自然底数e
eps %浮点运算的相对精度数据类型:
%%数字
1,2,3;%%向量
a=[2 4 6 8];
x=1:2:10;
x=linspace(1,10,10);%%矩阵
a=[2 4;6 8];%%字符串
'hello world'运算符
+ %算数加
- %算数减
* %算数乘
.* %点乘
^ %算数乘方
/ %算数右除
' %矩阵转置
== %等于常用函数
abs %模
sqrt %平方根
exp %e指数
sin %正弦函数第二部分:基础运算
变量赋值
%数值
a=3;%向量
b=[1 2 3];
c=[1,2,3];
d=linspace(1,3,3);
e=1:1:3;%矩阵
f=[1,2,3;4,5,6];%字符串
g='hello world';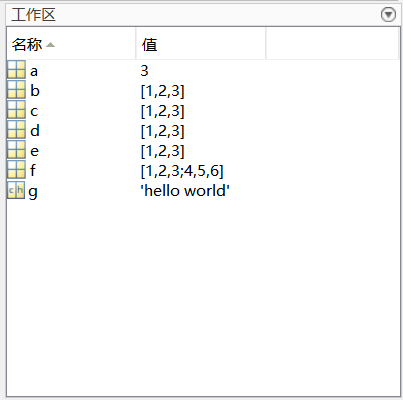
数学运算
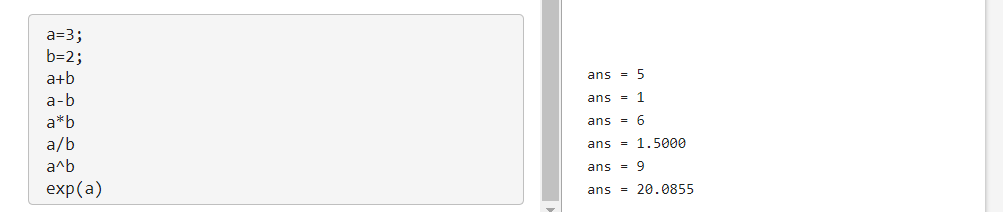
逻辑计算
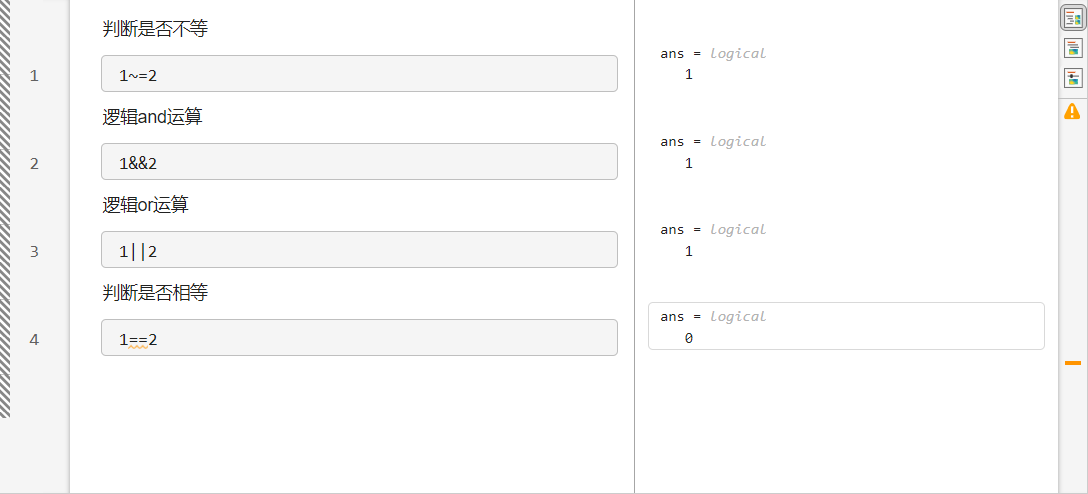
注释
%后面的是注释
CTRL+R快捷键注释
CTRL+T快捷键取消注释
第三部分:程序基础
程序设计
程序结构
循环结构:
for循环
for 变量=表达式可执行语句1
end2. while 循环
while 表达式可执行语句1
end分支结构
if 表达式语句1
else语句2
end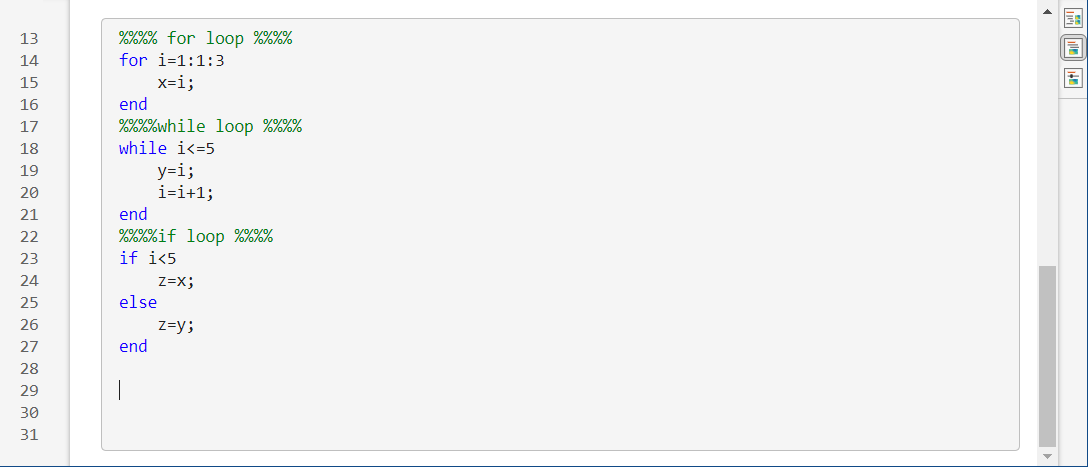
第四部分:函数句柄
直接通过@符号定义
fun1=@(参数1,参数2,...)函数表达式
myfun1=fun1(变量1,变量2)%example1
fun1=@(x,y)(x.^2+y.^2)
myfun1=fun1(2,3)%example2
x=1:1:10;
y=linspace(10,20,10);%10 11 12 13 14 15 16 17 18 19
fun2=@(x,y)(x.^2+y.^2)
myfun2=fun2(x,y)M文件定义和调用函数
%example
function[输出形参表:output1,output2,...,outputn]=函数名(输入形参表:input1,...,inputn)注释说明部分函数体代码部分
endmyfun1=fun1(x,y);function f1=fun1(x1,y1) %%一般这个定义函数部分都会放在这个程序的最下面f1=x1.^2+y1.^2;
end第五部分:画图基础
基础命令
figure | 创建一个图形窗口 |
close all | 关闭打开的matlab文件 |
hold on | 保持当前轴及图形不变 |
grid on | 显示当前坐标区的主网格线 |
plot(x,y) | 创建x-y的二维线图 |
polarplot(theta,rho) | 在极坐标中绘图 |
plot3(x,y,z) | plot(x,y)的三维拓展 |
plot(x1,y1;x2,y2...) | 绘制多条曲线 |
%example
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
%创建x,y变量
x=linspace(-pi,pi);
y=cos(x);
plot(x,y);
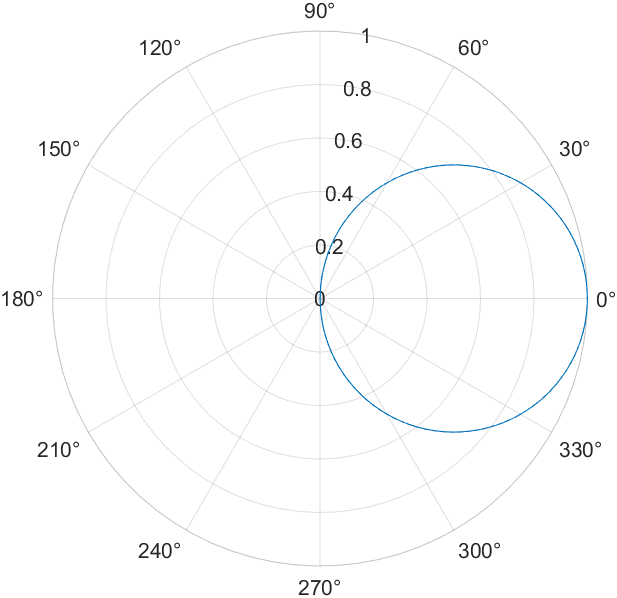
figure
polarplot(x,y)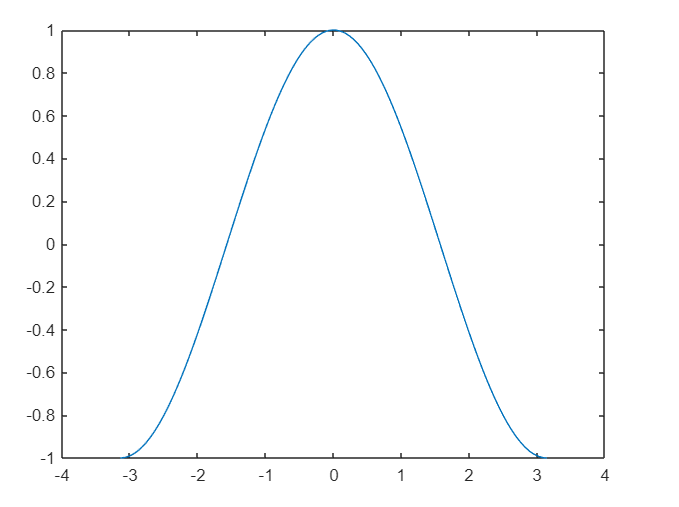
美化线条
plot(x,y,s) s为单引号标记的字符串,用来设 置所画数据点的类型、大小、颜色 以及数据点之间连线的属性。
'r' | red | '-' | 实线 | 'o' | 圆圈 |
'g' | green | '--' | 虚线 | '+' | 加号 |
'b' | blue | ':' | 点线 | '*' | 星号 |
'k' | black | '-.' | 点划线 | '.' | 点 |
LineWidth | 线宽 | ||||
%example
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
% x=linspace(-pi,pi);
% y=cos(x);
% plot(x,y);
% figure
% polarplot(x,y)
clc;
clf;
clear;
close;
x=linspace(-pi,pi);
y=cos(x);
%%plot(x,y,'r-o',LineWidth=0.5);
plot(x,y,'r-o','LineWidth',0.5);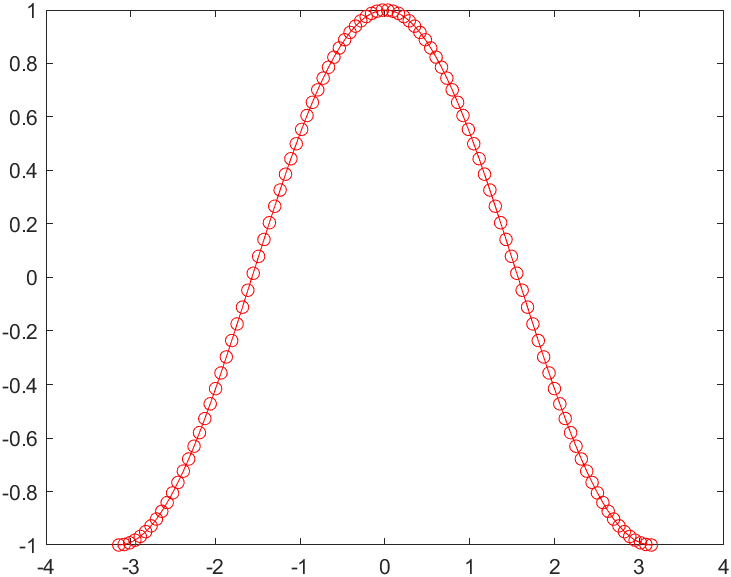
坐标轴设置
xlabel/ylabel | 坐标轴标签 |
xlim/ylim | 坐标轴范围调整 |
Axes 属性
官网中的Axes属性文档
%example1
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-pi,pi);
y=cos(x);
%%plot(x,y,'r-o',LineWidth=0.5);
plot(x,y,'r-o','LineWidth',0.5);
%修改Axes属性
ax=gca;%%获取图形信息
ax.FontSize=12;%%字体大小
ax.TickDir='out';%% 刻度线方向
ax.TickLength=[0.02 0.02];%%刻度线长度
ax.YLim=[-2 2];%%刻度范围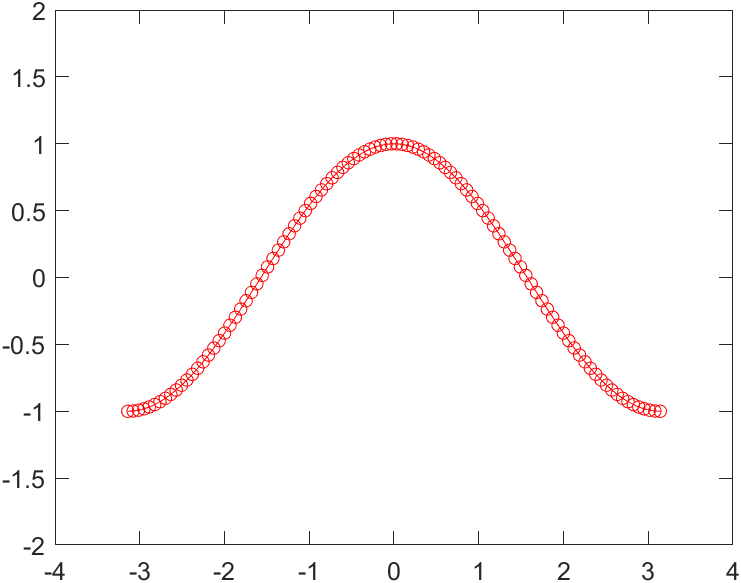
%example2
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-pi,pi);
y=cos(x);
%%plot(x,y,'r-o',LineWidth=2);
plot(x,y,'r-o','LineWidth',2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);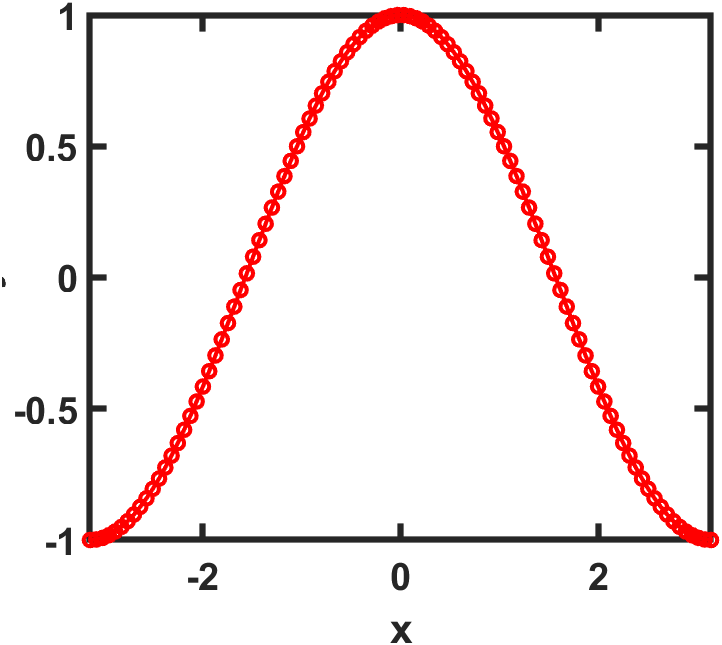
对数坐标轴
半对数坐标系 | |
semilogx(x,y) | x轴以10为基数的对数刻度 |
semilogy(x,y) | y轴以10为基数的对数刻度 |
双对数坐标系 | |
loglog(x,y) | x,y轴以10为基数的对数刻度 |
%example
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=0:1:1000;
y=0:10:1e4;
subplot(2,2,1);
semilogy(x,y);
subplot(2,2,2);
semilogx(x,y);
subplot(2,2,[3,4]);
loglog(x,y)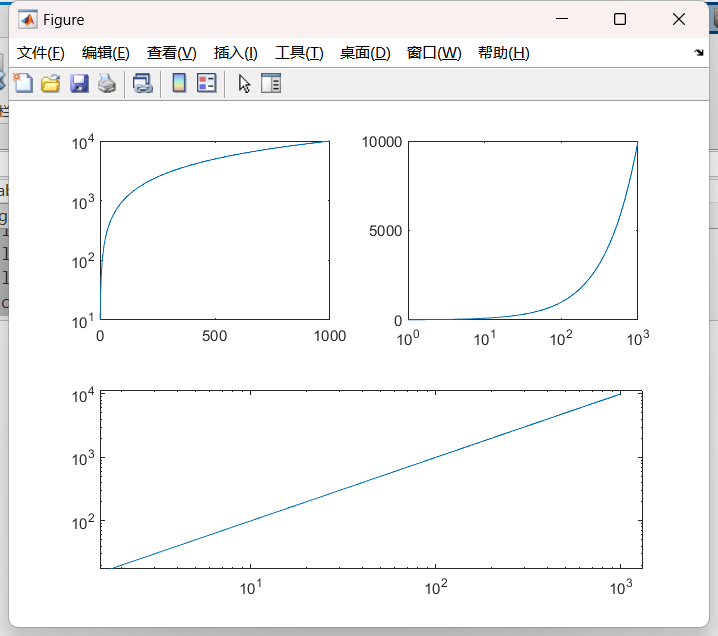
一图多线
hold on
plot(x1,y1,x2,y2,x3,y3...)
%example
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x1=linspace(-pi,pi);
y1=cos(x1);
%%plot(x,y,'r-o',LineWidth=2);
plot(x1,y1,'r-o','LineWidth',2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);hold on;%%保持图像不变x2=linspace(-pi,pi);
y2=sin(x2);
%%plot(x,y,'b--*',LineWidth=2);
plot(x2,y2,'b--*','LineWidth',2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);
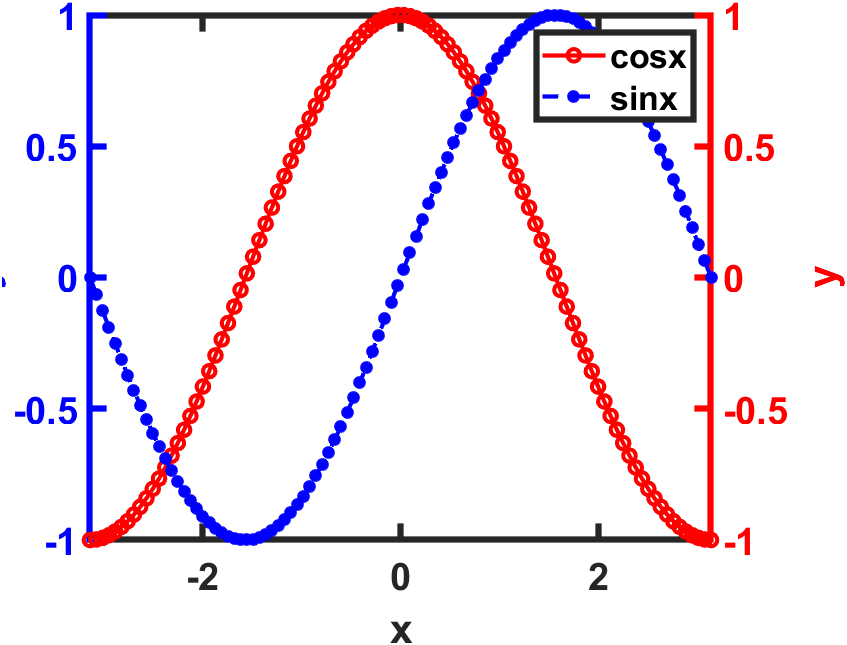
legend('cosx','sinx')%%多线条最好有图例说明一下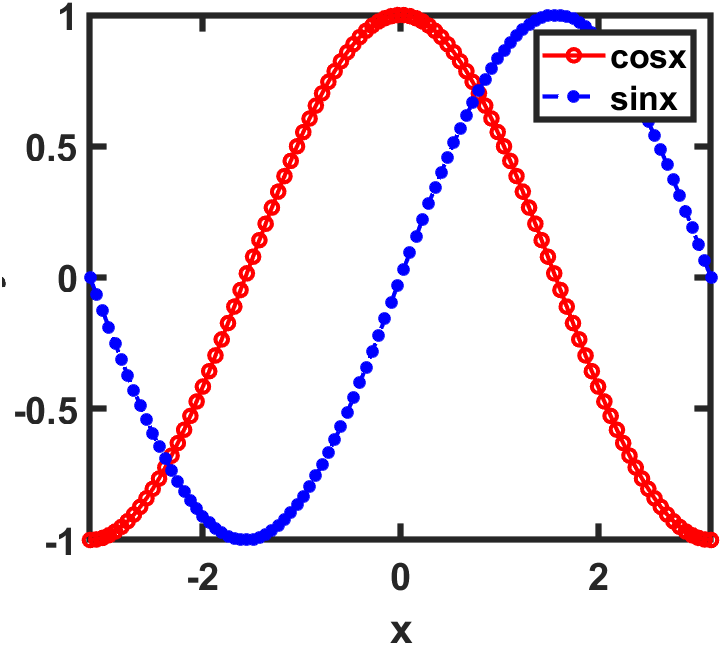
%该代码生成的图形和上图一样,最大的不同在于双线条的画法不同
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x1=linspace(-pi,pi);
y1=cos(x1);
x2=linspace(-pi,pi);
y2=sin(x2);
plot(x1,y1,'r-o',x2,y2,'b--*',LineWidth=2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);
legend('cosx','sinx')%%多线条最好有图例说明一下双纵坐标轴
yyaxis left
yyaxis right
%example
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x1=linspace(-pi,pi);
y1=cos(x1);
colororder({'b','r'});%设置坐标轴颜色
yyaxis left;
%%plot(x,y,'r-o',LineWidth=2);
plot(x1,y1,'r-o','LineWidth',2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);hold on;%%保持图像不变yyaxis right;
x2=linspace(-pi,pi);
y2=sin(x2);
%%plot(x,y,'b--*',LineWidth=2);
plot(x2,y2,'b--*','LineWidth',2);
%坐标轴
xlabel('x','FontSize',18,'FontWeight','bold');
ylabel('y','FontSize',18,'FontWeight','bold');
%set实现图形对象属性
set(gca,'Fontsize',18,'Fontweight','bold','Position',[0.1 0.16 0.71 0.8]);
set(gca,'LineWidth',3,'Tickdir','in','TickLength',[0.0215,0.015],'YMinorTick','off','XMinorTick','off');
%坐标轴范围
xlim([-pi pi]);
ylim([-1 1]);
legend('cosx','sinx')%%多线条最好有图例说明一下
多图形显示
常用:subplot(m,n,number)将当前窗口分割成mxn个视图区域 ,number表示第几分块
%example
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-pi,pi);
y1=cos(x);
y2=sin(x);subplot(1,2,1)
%%plot(x,y,'r-o',LineWidth=2);
plot(x,y1,'r-o','LineWidth',2);subplot(1,2,2)
%%plot(x,y,'b--*',LineWidth=2);
plot(x,y2,'b--*','LineWidth',2);不常用:tiledlayout(m,n) 将当前窗口分割成mxn个视图区域 nexttile 创建一个坐标区对象,再将其放 入当前图形窗口中的分块图布局 的下一个空图块中
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-pi,pi);
y1=cos(x);
y2=sin(x);figure;
tiledlayout(2,2);%%%在当前窗口布局为2*2的视图区域
nexttile%在第一个图块中创建一个坐标区对象
%%plot(x,y,'r-o',LineWidth=2);
plot(x,y1,'r-o','LineWidth',2);
nexttile%在第二个图块中创建一个坐标区对象
%%plot(x,y,'b--*',LineWidth=2);
plot(x,y2,'b--*','LineWidth',2);
nexttile([1 2])创建第三给图块,占据1行2列的坐标区
plot(x,y1,x,y2)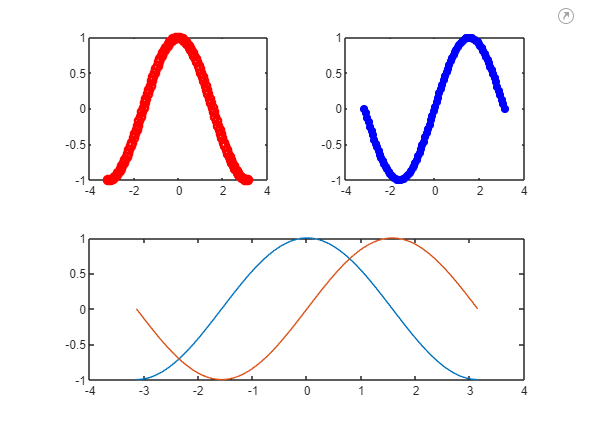
第六部分:特殊图形
伪彩图
二元函数z=f(x,y)
imagesc(x,y,Z)
pcolor(x,y,Z)
%imagesc
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-4,4,100);%%定义俩个相同的向量x,y
y=x;[X,Y]=meshgrid(x,y);%%%基于向量下x,y创建二维网格数据矩阵X,Y
Z=X.*exp(-X.^2-Y.^2);%%%使用函数表达式定义矩阵z
imagesc(x,y,Z)
xlabel('x');
ylabel('y');
colormap jet %%%设置当前颜色图
colorbar('FontSize',12);%%%显示色阶的颜色栏
clim([-1,1]);%%颜色栏的取值范围c=colorbar;
c.Label.String='Z';%%给颜色栏添加文字标注
c.Label.FontSize=12;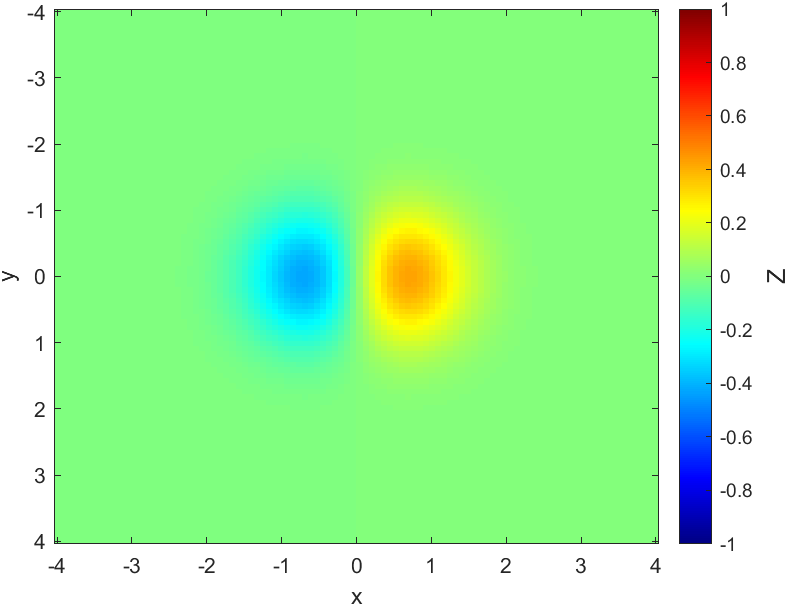
%pcolor
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-4,4,100);%%定义俩个相同的向量x,y
y=x;[X,Y]=meshgrid(x,y);%%%基于向量下x,y创建二维网格数据矩阵X,Y
Z=X.*exp(-X.^2-Y.^2);%%%使用函数表达式定义矩阵z
pcolor(x,y,Z)
xlabel('x');
ylabel('y');
colormap jet %%%设置当前颜色图
colorbar('FontSize',12);%%%显示色阶的颜色栏
clim([-1,1]);%%颜色栏的取值范围c=colorbar;
c.Label.String='Z';%%给颜色栏添加文字标注
c.Label.FontSize=12;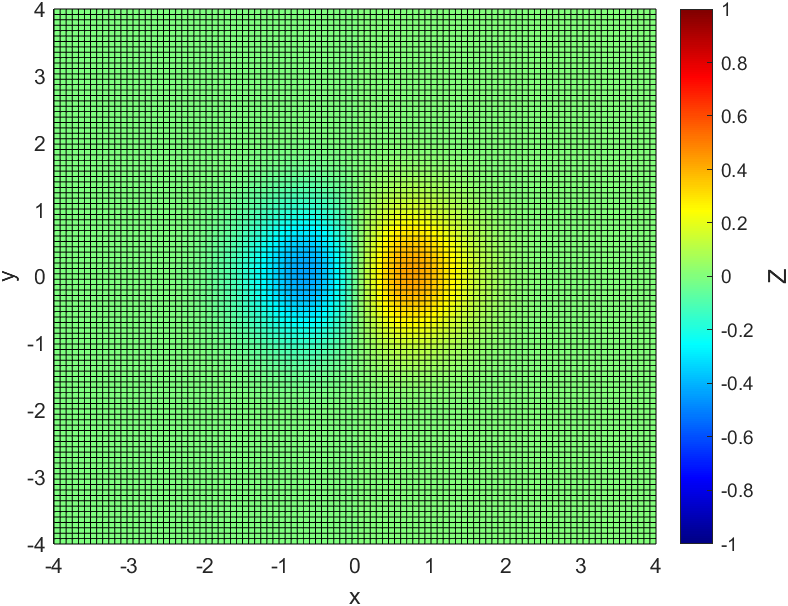
统计图形
bar(x,y) | 竖直条形图 | pie(x,y) | 饼图 |
barh(x,y) | 水平条形图 | histogram | 柱状图 |
area(x,y) | 面积图 |
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
y=randn(20,1); %%创建正态分布的随机数矩阵y
tiledlayout(2,2);
%%%bar函数绘制条形图
nexttile;
bar(y,1,'r');%%1表示条形图的宽度,r表示颜色
title('条形图');
%%%area函数绘制面积图
nexttile;
area(y,'LineStyle',':');%%设置线宽和线型
title('面积图');
%%%pie函数绘制饼图
nexttile;
pie(y);
title('饼图');
%%%histogram函数绘制柱状图
nexttile;
histogram(y,10,'FaceColor','r');%%数字10指定bin数目
title('柱状图');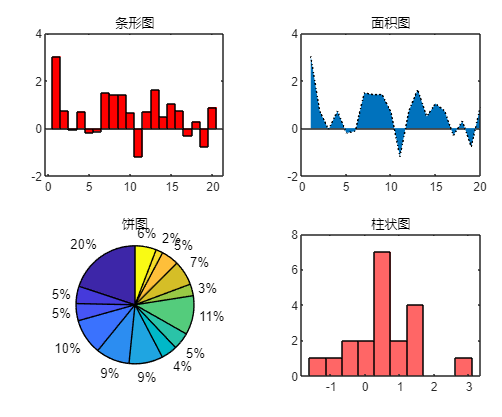
离散数据图形
errorbar(x,y,err) | 误差棒图 |
stem(x,y) | 火柴杆图 |
stairs(x,y) | 阶梯图 |
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=[93.3 93.1 94.7 90.1 95.6 90.0 94.7];
y=[85.6 94.9 96.2 95.1 95.8 96.3 94.1];
e=abs(x-y);
tiledlayout(2,2);
nexttile;
errorbar(y,e);
title('误差棒图');
x=-2:0.1:2;
y=exp(x);
z=exp(-x);
nexttile;
stem(x,y);
title('二维火柴图');
nexttile;
stem3(x,y,z);
title('三维火柴图');
nexttile;
stairs(x,y);
title('阶梯图');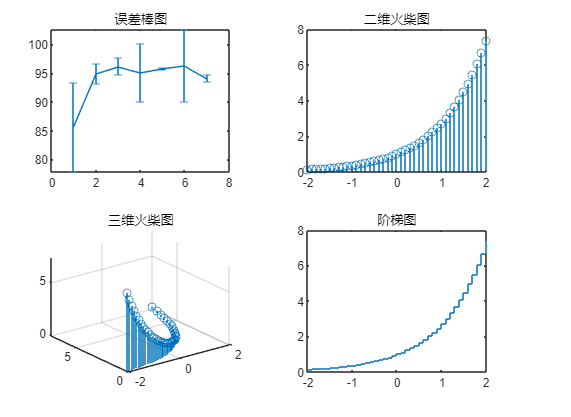
向量图形
compass(U,V) | 罗盘图 |
feather(U,V) | 羽毛图 |
quiver(U,V) | 箭头图/矢量图 |
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-4,4,50);%%定义俩个相同的向量x,y
y=x;[X,Y]=meshgrid(x,y);%%%基于向量下x,y创建二维网格数据矩阵X,Y
Z=X.*exp(-X.^2-Y.^2);%%%使用函数表达式定义矩阵z
[U,V]=gradient(Z,2,2);
contour(X,Y,Z);
hold on;
quiver(X,Y,U,V);
axis image
xlim([-2 2]);
ylim([-2 2]);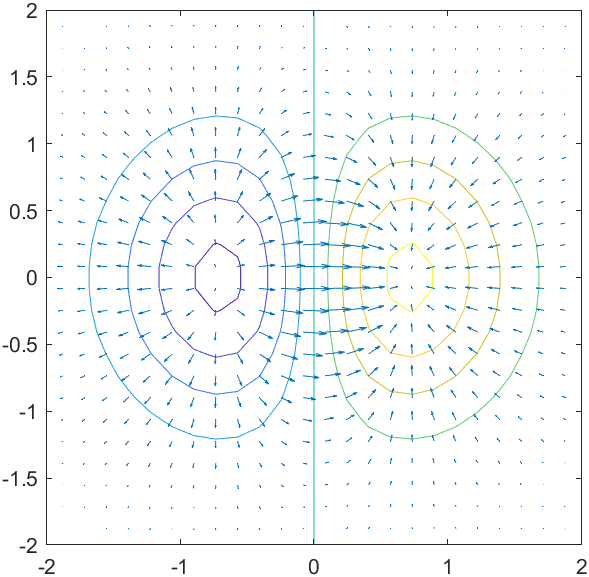
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=-pi:pi/10:pi;%%定义俩个相同的向量x,y
y=sin(x);
subplot(1,2,1);
compass(x,y);
title('罗盘图');
subplot(1,2,2);
feather(x,y);
title('羽毛图')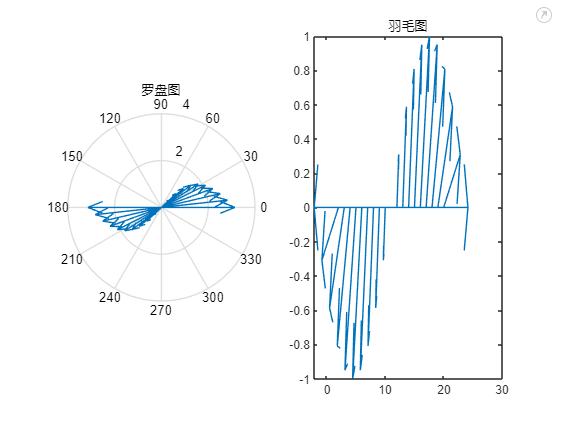
三维绘图
plot3(x,y,z) | plot的三维拓展 |
mesh(X,Y,Z) | 绘制三维网格图 |
surf(X,Y,Z) | 绘制三维曲面图 |
contour(X,Y,Z) | 绘制二维等值线 |
contourf(X,Y,Z) | 绘制二维等值线 |
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
x=linspace(-4,4,50);%%定义俩个相同的向量x,y
y=x;[X,Y]=meshgrid(x,y);%%%基于向量下x,y创建二维网格数据矩阵X,Y
Z=X.*exp(-X.^2-Y.^2);%%%使用函数表达式定义矩阵z
[U,V]=gradient(Z,2,2);%%%设置矩阵梯度tiledlayout(3,2)
nexttile
mesh(X,Y,Z);
title('网格图');
xlim([-2 2]);
ylim([-2 2]);nexttile
surf(X,Y,Z);
title('曲面图');
xlim([-2 2]);
ylim([-2 2]);nexttile
contour(X,Y,Z,20);
title('二维等值线图');
xlim([-2 2]);
ylim([-2 2]);nexttile
contourf(X,Y,Z,20);
title('填充二维等值线图');
xlim([-2 2]);
ylim([-2 2]);nexttile
quiver(X,Y,U,V);
title('梯度图');
xlim([-2 2]);
ylim([-2 2]);nexttile
streamslice(X,Y,U,V);
title('密度梯度流线图');
xlim([-2 2]);
ylim([-2 2]);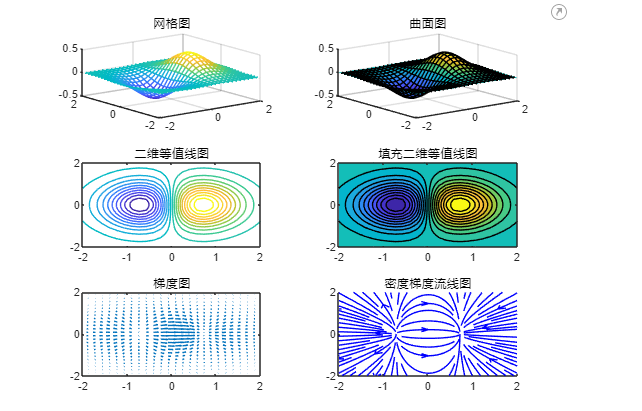
第七部分:方程求解
代数方程求解
poly2sym | 使用系数向量表示;输出结果为字符 |
roots | 求多项式的根 |
fzero(fun,x0) | 函数找到x0附近函数fun(x)的零点 |
%poly2sym 使用系数向量表示;poly2sym输出结果为字符
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
p1=[1 2 3];
p2=[2 3 1];
p3=[1 1 2 3 4 5];
poly2sym(p1)
poly2sym(p2)
poly2sym(p3)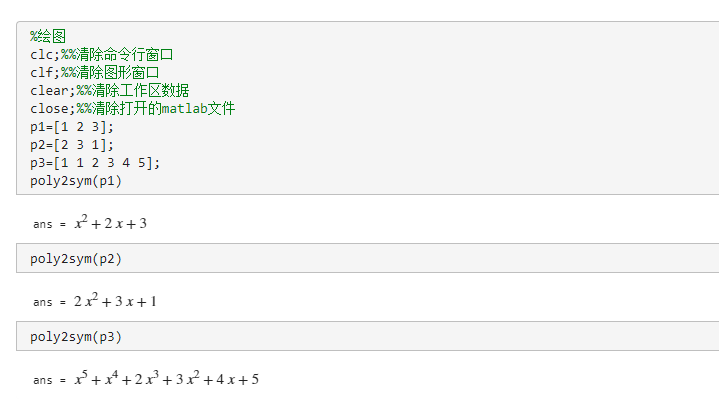
%roots求解多项式的根
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
p1=[1 2 3];
p2=[2 3 1];
p3=[1 1 2 3 4 5];
r1=roots(p1);
r2=roots(p2);
r3=roots(p3);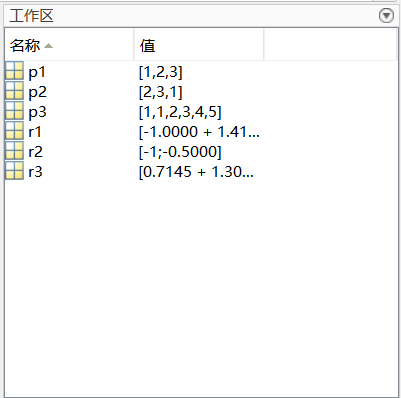
%fzero函数找到x0附近函数fun(x)的零点
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
myfun=@(x,a)cos(a*x);
a=2;
fun=@(x)myfun(x,a);
x0=fzero(fun,0.1);
x=fzero(fun,0.1);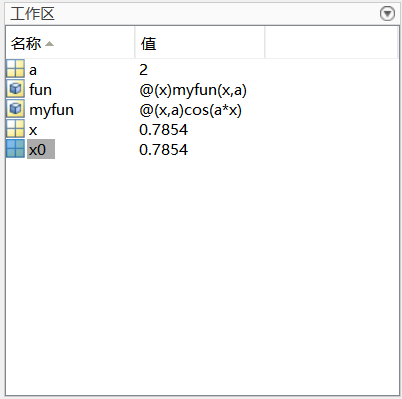
常微分方程求解
龙格-库塔方法(Runge-Kutta) :基本求解器选择 ode45 适用于大多数 ODE 问题,一般情况下应作为您的首选求解器。但对于精 度要求更宽松或更严格的问题而言,ode23、ode78、ode89 和 ode113 可能比 ode45 更加高效。
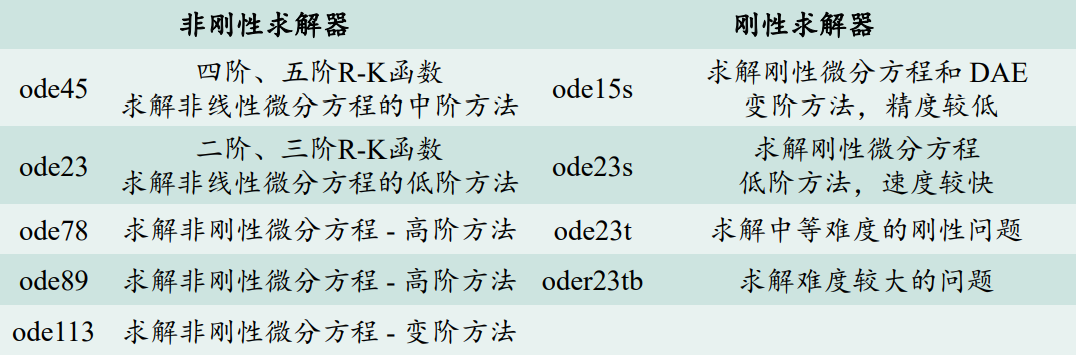
非刚性求解器 | 刚性求解器 | ||
ode45 | 四阶、五阶R-K函数求解非线性微分方程的中阶方法 | ode15s | 求解刚性微分方程和 DAE 变阶方法,精度较低 |
ode23 | 二阶、三阶R-K函数 求解非线性微分方程的低阶方法 | ode23s | 求解刚性微分方程 低阶方法,速度较快 |
ode78 | 求解非刚性微分方程 - 高阶方法 | ode23t | 求解中等难度的刚性问题 |
ode89 | 求解非刚性微分方程 - 高阶方法 | oder23tb | 求解难度较大的问题 |
ode113 | 求解非刚性微分方程 - 变阶方法 | ||
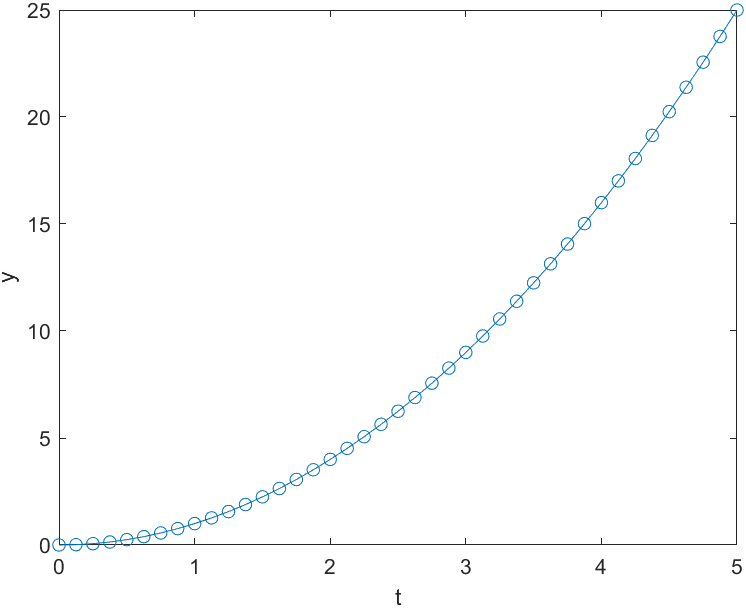
例如:利用R-K方法求解微分方程dy/dt=2t,其中0<t<5,y(0)=0。
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
tspan=[0 5];%积分区间定义
y0=0;%初始条件
[t,y]=ode45(@(t,y)2*t,tspan,y0);%%%计算微分方程在指定积分区间的积分
plot(t,y,'-o');
xlabel('t');
ylabel('y');
利用R-K方法求解微分方程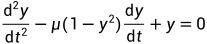 ,其中
,其中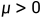 .
.
当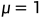 ,将方程转换成一阶常微分方程:
,将方程转换成一阶常微分方程: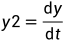 和
和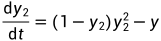
%绘图
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
tspan=[0,20];
mu=1;
y0=[2 0];
[t,y]=ode45(@(t,y)fun(t,y),tspan,y0);
plot(t,y(:,1),'ro-',t,y(:,2),'k:p','LineWidth',2);
function dydt=fun(~,y)dydt=zeros(2,1); dydt(1)=y(2);dydt(2)=(1-y(1).^2).*y(2)-y(1);
end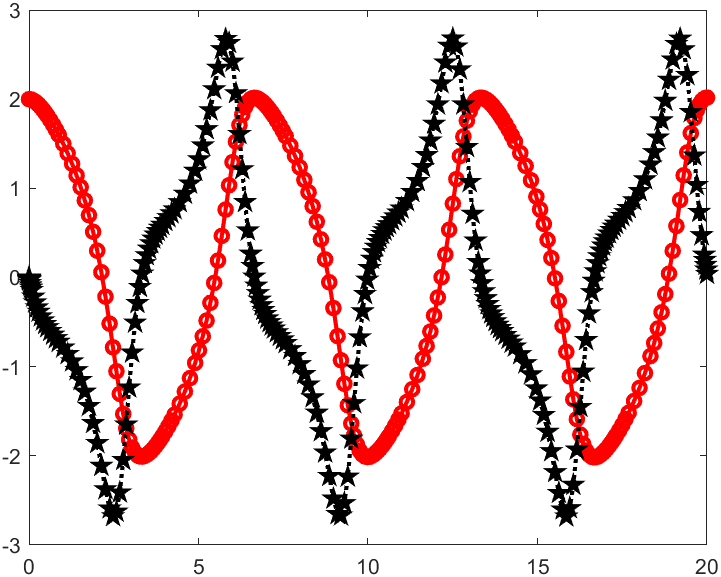
数值积分
数值积分官网
int(f) | 求函数f的原函数 |
int(f,a,b) | 求函数f在[a b]上的定积分 (解析解) |
integral(f,a,b) | 求函数f在[a b]上的定积分 (数值解) |
integra2l(f,xmin,xmax,ymin,ymax) | 求函数f的二重积分 |
trapz | 求离散数据的数值积分 |
clc;%%清除命令行窗口
clf;%%清除图形窗口
clear;%%清除工作区数据
close;%%清除打开的matlab文件
%普通数值积分
fun1=@(x)exp(-x.^2).*log(x).^2;
q1=integral(fun1,0,Inf)
%参数化函数数值积分
fun2 = @(x,c) 1./(x.^3-2*x-c);
q2 = integral(@(x) fun2(x,5),0,2)
%积分限为奇异点的数值积分
fun3 = @(x)log(x);
q3 = integral(fun3,0,1,'RelTol',0,'AbsTol',1e-12)
%复函数的围道积分
fun4 = @(z) 1./(2*z-1);
q4 = integral(fun4,0,0,'Waypoints',[1+1i,1-1i])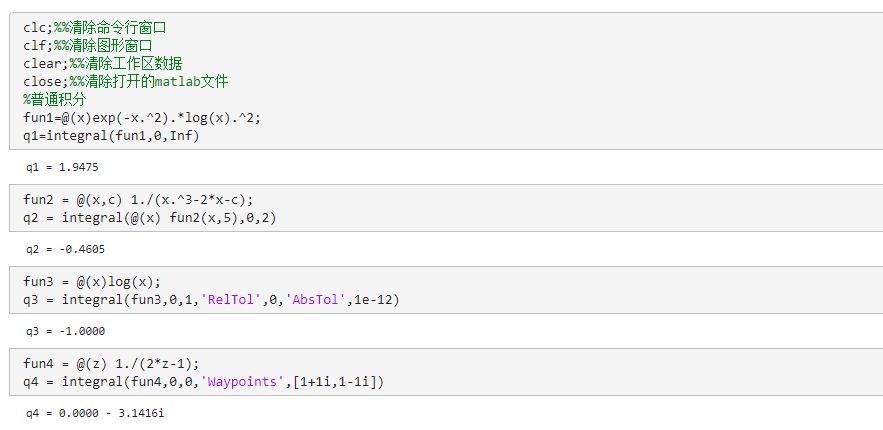
第八部分:数据拟合
安装数据拟合器---Curve Fitting Toolbox
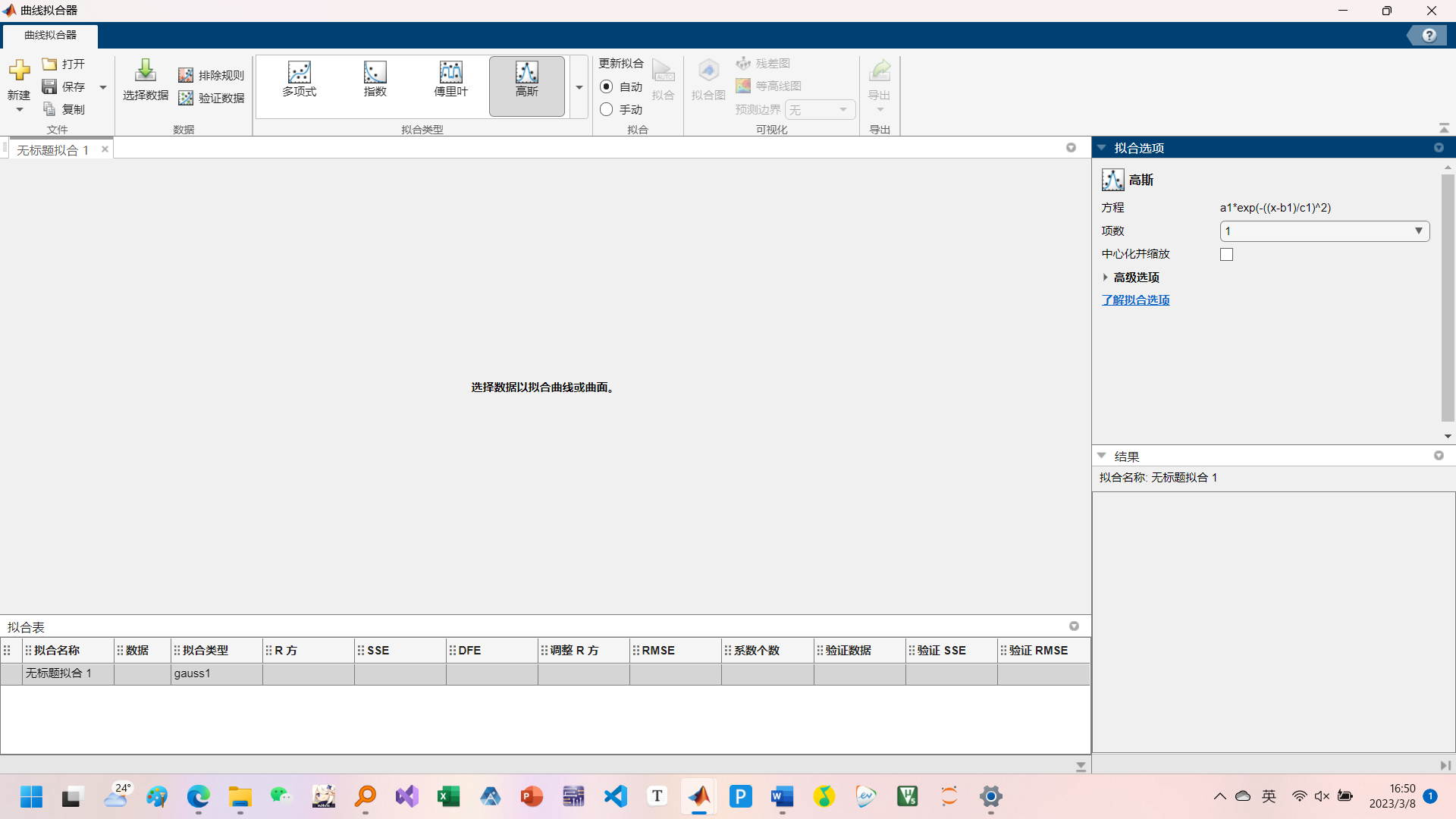
polyfit(x,y,n) | 用二乘法对已知数据x,y进行拟合,以 求得n阶多项式系数向量 |
linefit(x,y) | 最小二乘法直线拟合 |
相关文章:

MATLAB的快速入门
第一部分:基础知识常用命令:clc %清除命令行窗口 clear %清空工作区数据 cd %显示或改变工作目录 clf %清除图形窗口 help %打开帮助文档 save %保存内存变量到指定文件 hold %保持图形 close %关闭当前图窗 quit %退出变量&#x…...

Python中赋值、引用、深浅拷贝的区别和联系
文章目录一、对象的唯一id二、赋值三、可变对象和不可变对象四、函数的参数传递五、深拷贝和浅拷贝六、举个栗子6.1 不可变对象的拷贝6.2 可变对象的拷贝6.3 可变对象改变外层元素6.4 可变对象改变内层元素七、总结一、对象的唯一id python中的所有对象都有自己的唯一id&#…...

春招冲刺(十一):前端面试之网络总结
网络总结 Q1: GET和POST的请求的区别 应用场景:Get是一个幂等请求,一般用于请求资源。post不是幂等请求,一般用于修改资源。缓存:Get请求一般缓存,Post一般不缓存报文格式:Get请求体一般为空,…...

Mybatis插件
插件使用 动手实现plugin 首先我们需要实现一下这个Interceptor,其中plugin和setProperties方法可以不实现,plugin是因为已经有了完善的逻辑,而setProperties,如果不需要在intercept()中使用属性,也可以不设置。然后…...
)
计算机学科专业基础综合科目(408)
文章目录408 第一章 数据结构数据是客观事物的符号表示,是对现实世界的事物采用计算机能够识别,存储和处理的形式进行描述的符号的集合。 数据元素是数据的基本单位。一个数据元素由若干个数据项组成。数据项又成为简单数据项及复合数据项两种。简单数据…...
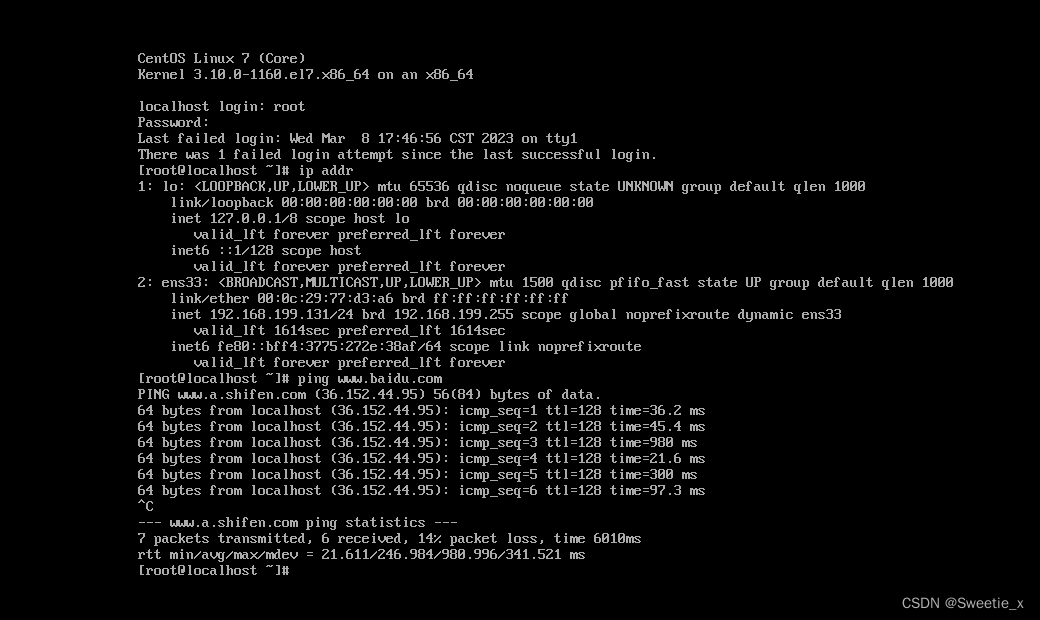
centos7安装教程
1.点击文件–新建虚拟机 2.根据图片一直下一步或者做一些改动 3. 点击自定义硬件,点击浏览选中下载好的ISO文件 4.配置完成后启动虚拟机 5.选择语言,中英文都可,按需求选择 6.进行设置目标位置,配置分区 7.选择网络和主机名 8.配置…...

Kafka 重平衡
Kafka 重平衡协调者RebalanceRebalance 条件Rebalance 避免Rebalance : 让单 Group 下所有的 Consumer 怎么消费订阅主题的所有分区Rebalance 时 , 所有 Consumer 要共同参与 (无法消费),在协调者 (Coordinator) 协调下,完成订阅主题分区的分配 协调者…...
)
PTA:L1-022 奇偶分家、L1-023 输出GPLT、L1-024 后天(C++)
目录 L1-022 奇偶分家 问题描述: L1-023 输出GPLT 问题描述: 实现代码: L1-024 后天 问题描述: 实现代码: 简单题,没写题解,看代码就能看懂 L1-022 奇偶分家 问题描述: 给…...
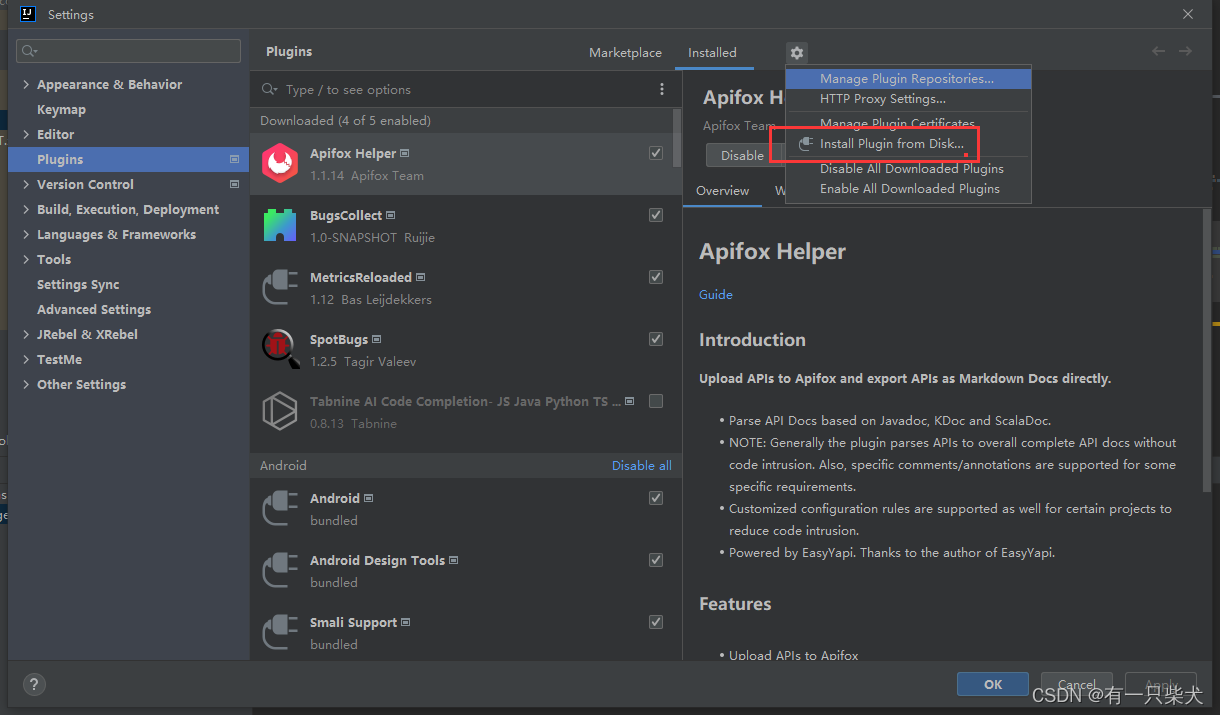
IDEA插件开发入门.02
前言许久没更新IDEA插件开发系列了。最近刚好在汇总日常开发中常见的代码“异味”,共享文档复制黏贴略显麻烦,所以想着是否可以搞一个IDEA插件来帮忙收集常见代码,毕竟IDEA作为后端程序员必备的开发工具,显然会方便很多。于是&…...

如何用 23 种编程语言说“Hello World”
在编程的世界里," Hello World " 往往是开发者开始学习一种新语言时写的第一个程序。这个简单的程序会将 “Hello World“ 输出在我们的屏幕上。看似很简单的行为,实际上对于每一个新学习编程语言的人来说,它代表着新的起点。那么&…...

【Linux快速入门】文件目录操作
文章目录概念1. Linux文件系统概述2. Linux文件目录结构3. Linux文件和目录操作3.1 文件操作3.1.1 创建文件3.1.2 复制文件3.1.3 移动文件3.1.4 删除文件3.1.5 查看文件3.1.6 输出指令3.1.7 >和>>指令3.2 目录操作3.2.1 创建目录3.2.2 复制目录3.2.3 移动目录3.2.4 删…...
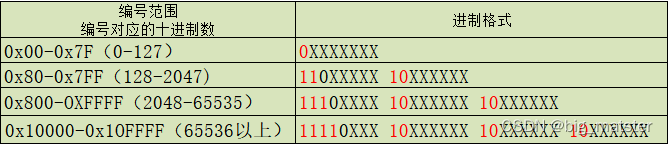
字体反爬慢慢总结破解方式
什么是字体反爬 网页开发者自己创造一种字体,因为在字体中每个汉字都有其代号,那么以后再网页中不会直接显示这个文字的效果。而是显示其代号,因此即使获取了网页的文本内容。也只是获取到文字的代号,而不是文字本身。 简单来说&…...

Kafka 位移提交
Kafka 位移提交自动提交手动提交Consumer 的消费位移 : 记录 Consumer 下一条消息的消费位移 如 : Consumer 已消费 5 条消息 (位移: 0 - 4) , 此时 Consumer 位移 5 : 指向下一条消息的位移 提交位移 (Committing Offsets) : Consumer 向 Kafka 汇报位移数据 Consumer 能同…...
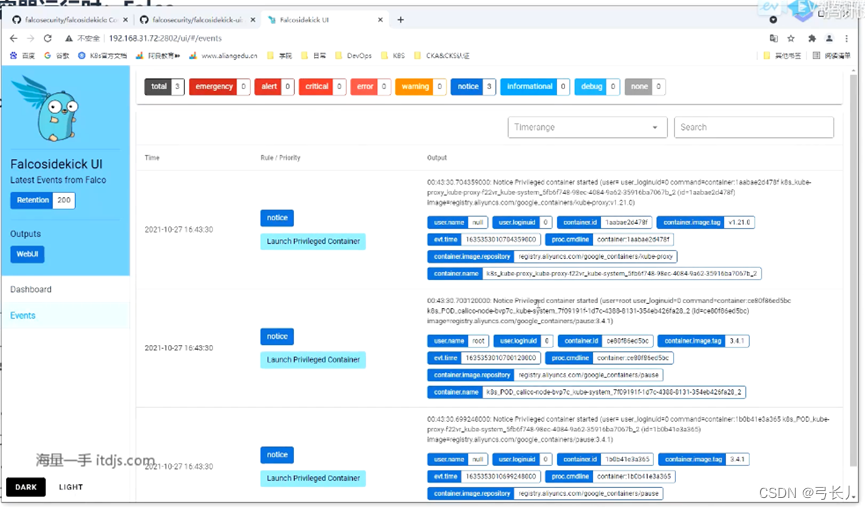
kubernetes--监控容器运行时:Falco
目录 Falco介绍 Falco架构 Falco的安装 告警规则示列 威胁场景测试: 监控容器创建的不可信任进程(自定义规则) Falco支持五种输出告警方式falco.yaml: Falco告警集中化展示: Falco介绍 Falco是一个Linux安全工具…...
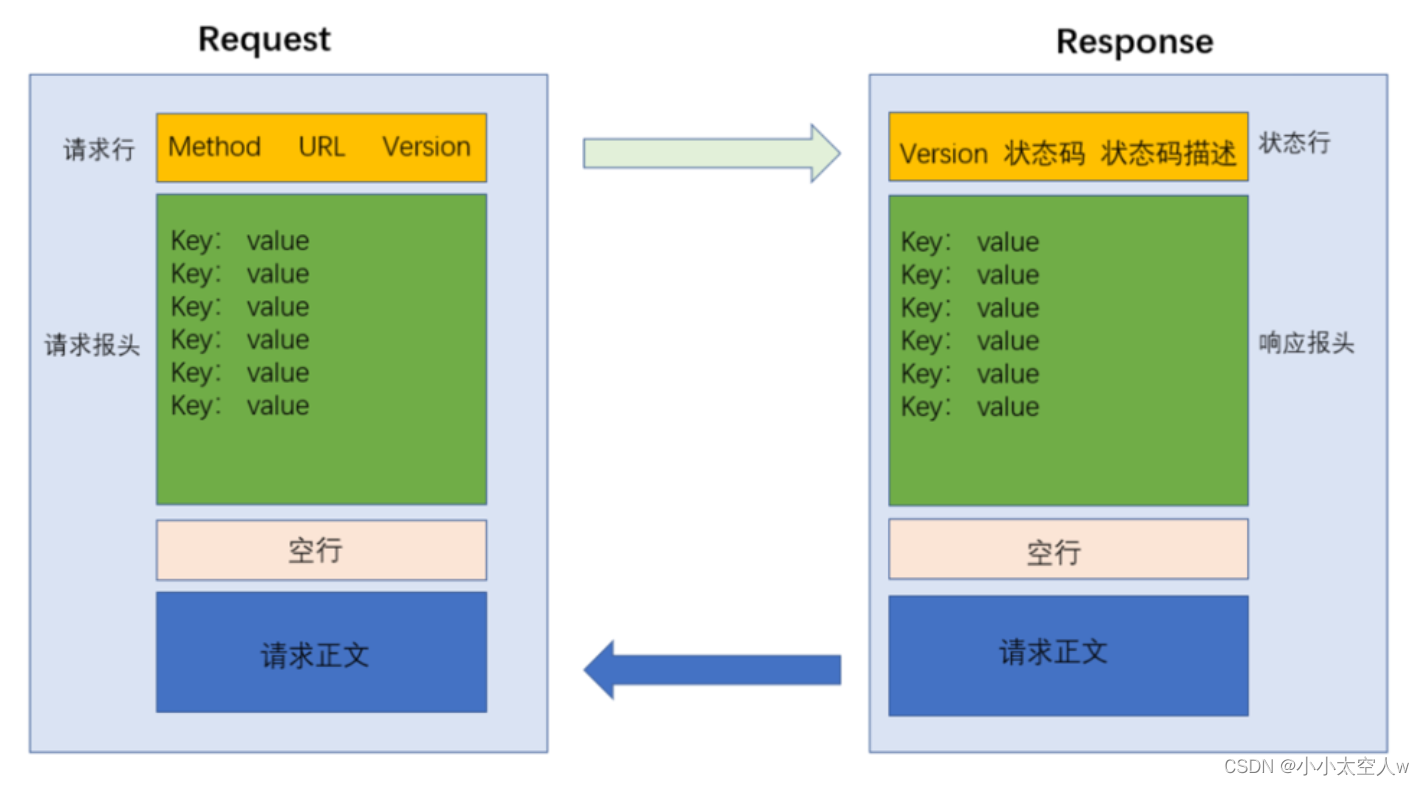
HTTP协议详解(上)
目录 前言: 认识URL HTTP协议方法 通过Fiddler抓包 GET和POST之间典型区别 header详解 HTTP响应状态码 常见状态码解释 状态码分类 HTTP协议报文格式 小结: 前言: HTTP协议属于应用层协议,称为超文本传输协议ÿ…...

java性能-原生内存-内存分析
原生内存最佳实践 内存占用 jVM使用的原生内存和堆内存总和就是一个应用程序的总内存——操作系统角度 jvm启动时候加载的类路径下的jar文件相关的内存和系统其他进程共享资源的可能 测量内存占用 线程是个例外——每当创建一个线程操作系统都会分配一些原生内存存储线程栈…...
c++类与对象
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章 🔥座右铭:“不要等到什么都没有了,才下定决心去做” …...
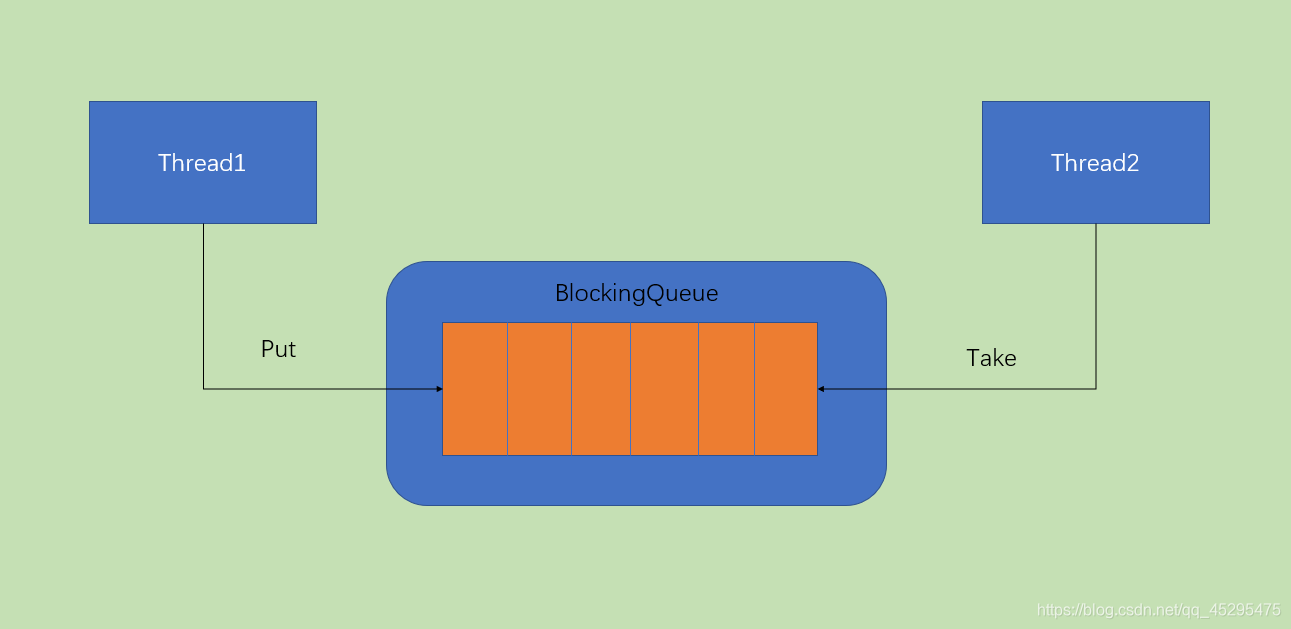
Java并发编程与API详解
文章目录前言操作系统——进程和线程进程进程组成进程状态进程控制进程创建进程终止进程阻塞和唤醒进程通信线程线程组成线程状态线程控制线程的实现方式用户线程内核线程混合方式CPU调度调度的层次调度的实现调度器调度的时机、切换与过程进程调度的方式闲逛进程两种线程的调度…...
【冲刺蓝桥杯的最后30天】day5
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...

大厂与小厂招人的区别,看完多少有点不敢相信
前两天在头条发了一条招人的感慨,关于大厂招人和小公司招人的区别。 大厂:有影响力,有钱,能够吸引了大量的应聘者。因此,也就有了筛选的资格,比如必须985名校毕业,必须35岁以下,不能…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
