探索数据结构
什么是数据结构
数据结构是由:“数据”与“结构”两部分组成
数据与结构
数据:如我们所看见的广告、图片、视频等,常见的数值,教务系统里的(姓名、性别、学号、学历等等);
结构:当我们面对海量的数据时,我们时常无法下手,寻找数据是不方便的,可读性就很差;而结构则是将这些数据以各种不同的形式进行排序,使我们便于寻找;
数据结构:是计算机存储、组织数据的方式。是数据之间存在一种或多种相互关系的集合;

什么是算法
算法(Algorithm)就是定义良好的计算过程,他取出一个或一组数据为输入,产出一个或一组的值为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
算法一般分为:排序,递归与分治,回溯,DP,贪心,搜索算法、二分查找、水桶法等等;
- 算法往往数学密切相关,就如数学题一样,每道数学题都有不同的解法,算法也是同理
复杂度分析
我们如何评判算法的效率呢,问题的解决方法有很多,对于计算机而言,我们需要找到问题的最优解,为了寻找到这个最优解,我们需要从两个维度评判
- 时间效率:算法运行的快慢
- 空间效率:算法所占空间的大小
评估方法:实验分析与理论分析
对于实验分析而言:
- 相同的算法在不同的电脑,它们所运行的时间也许会有很大的出入;
- 当面对大量的数据而言,同一台电脑时间上的差距则会变为很大,导致误差的增大;
- 有些算法在少量数据时运算速度不快,在大量数据中反之;
由于实验分析法的局限性,就有人提出了一种理论测评的方法,就是渐近复杂度分析(asymptotic complexity analysis),简称复杂度分析。
这种方法体现算法运行所需的时间(空间)资源与输入数据大小之间的关系,能有效的反应算法的优劣。
时间复杂度与空间复杂度
时间复杂度
指一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。让我们计算下方代码的时间复杂度
int main()
{int n=10;//对于时间复杂度而言,当数据为n时,下方代码区,运行次数10,时间复杂度为O(n)while (n--) {printf("%d", n);}//在时间复杂度中,我们会忽略除最高次的所有项//忽略所有系数return 0;
}实际上我们不可能对执行次数的统计精确,并且为理论分析,当n->∞时,最高次的影响会远远超过非最高次的项,所以O(n)的数量级由最高次决定,所以当我们计算时间复杂度时,可以简化为以下两个步骤
- 忽略除最高次的所有项
- 忽略所有系数
思考:
当我们遍历下方数组,查找2时,我们需要4次;

当长度为n的数组中存放的是无序自然数时,他们是没有规则的,此时我们查找2的次数:[ 1 , n ]
此时我们需要将最坏的情况作为时间复杂度
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度的表示也遵循大O的渐进表示法
让我们计算一下冒泡排序的空间复杂度
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}//在冒泡排序中,我们只开辟了一块空间,所以空间复杂度为O(1);复杂度的分类
算法的复杂度有几个量级,表示如下:
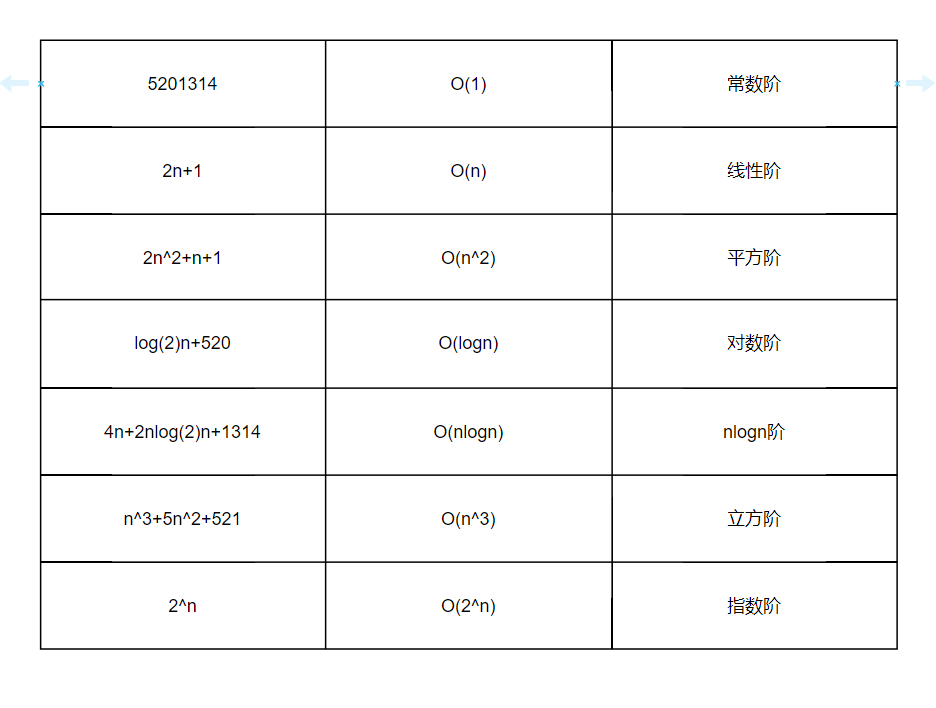
O(1)<O(logN)<O(N)<O(NlogN)<O(N2)<O(2N)<O(N!)
如图下列:
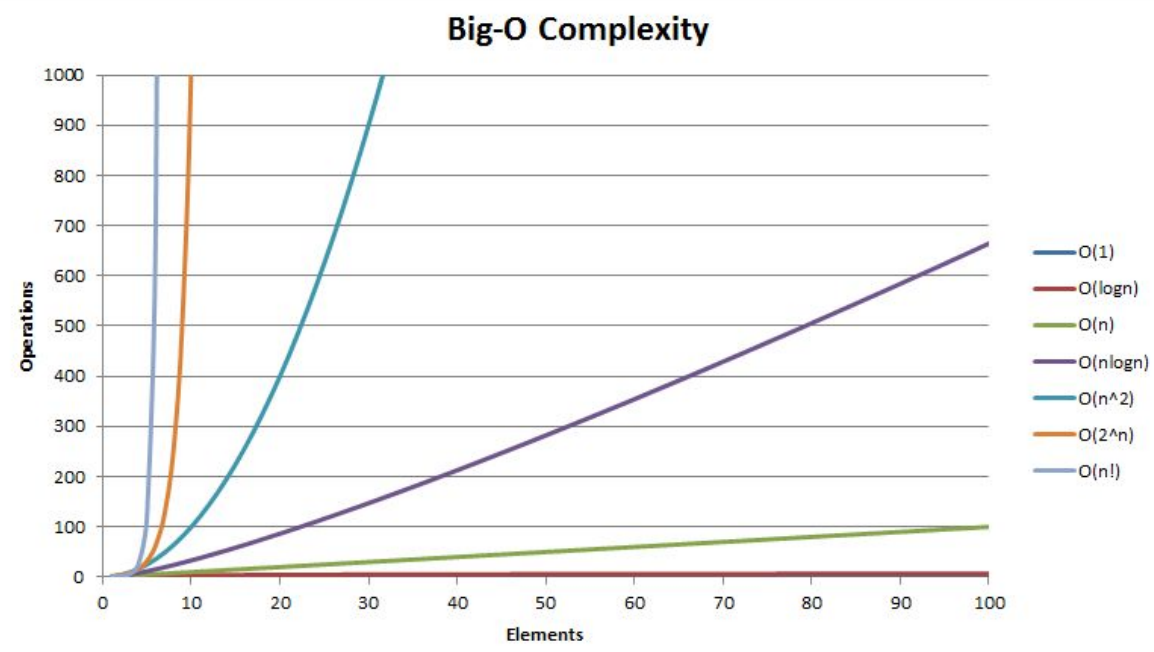
常数阶O(1)
int main()
{int n = 4;while (n--) {printf("%d", n);//执行次数为常数}return 0;
}对数阶O(logn)
int binary_search(int nums[], int size, int target)
//nums是数组,size是数组的大小,target是需要查找的值
{ int left = 0;int right = size - 1; // 定义了target在左闭右闭的区间内,[left, right]while (left <= right) { //当left == right时,区间[left, right]仍然有效int middle = left + ((right - left)>>1);//等同于 (left + right) / 2,防止溢出if (nums[middle] > target) {right = middle - 1; //target在左区间,所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; //target在右区间,所以[middle + 1, right]} else { //既不在左边,也不在右边,那就是找到答案了return middle;}}//没有找到目标值return -1;
}
线性阶O(n)
int main()
{int n;scanf("%d", &n);int court = 0;for (int i = 0; i < n; i++) {court += i;//计算和}return 0;
}以下为空间复杂度为O(n)
int main()
{int n;scanf("%d", &n);int* p = (int*)malloc(sizeof(int) * n);//开辟大小为n的空间if (p == NULL){perror("malloc fail");return -1;}free(p);p = NULL;}线性对数阶O(nlogn)
无论是时间复杂度还是空间复杂度,线性对数阶都是在循环嵌套里实现,即为一层为O(n),另一层为O(logn);
所以我们可以利用二分查找+打印
int binary_search(int nums[], int size, int target) //nums是数组,size是数组的大小,target是需要查找的值
{int left = 0;int right = size - 1; // 定义了target在左闭右闭的区间内,[left, right]while (left <= right) { //当left == right时,区间[left, right]仍然有效int middle = left + ((right - left) / 2);//等同于 (left + right) / 2,防止溢出if (nums[middle] > target) {right = middle - 1; //target在左区间,所以[left, middle - 1]}else if (nums[middle] < target) {left = middle + 1; //target在右区间,所以[middle + 1, right]}else { //既不在左边,也不在右边,那就是找到答案了printf("%d ", nums[middle]);}}//没有找到目标值return -1;
}void func(int nums[], int size, int target)
{for (int i = 0; i < size; i++){binary_search(nums, size, target);}
}平方阶O(n)
莫过于我们最为熟悉的冒泡排序
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}指数阶O(2^n)
指数阶的算法效率低下,并不常见
最为常见的指数阶为递归实现斐波那契数列
int Fib1(int n)
{if (n == 1 || n == 2){return 1;}else{return Fib1(n - 1) + Fib1(n - 2);}
}
相关文章:

探索数据结构
什么是数据结构 数据结构是由:“数据”与“结构”两部分组成 数据与结构 数据:如我们所看见的广告、图片、视频等,常见的数值,教务系统里的(姓名、性别、学号、学历等等); 结构:当…...

VMware虚拟机中ubuntu使用记录(6)—— 如何标定单目相机的内参(张正友标定法)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、张正友相机标定法1. 工具的准备2. 标定的步骤(1) 启动相机(2) 启动标定程序(3) 标定过程的操作(5)可能的报错 3. 标定文件内容解析 前言 张正友相机标定法…...
每日OJ题_记忆化搜索②_力扣62. 不同路径(三种解法)
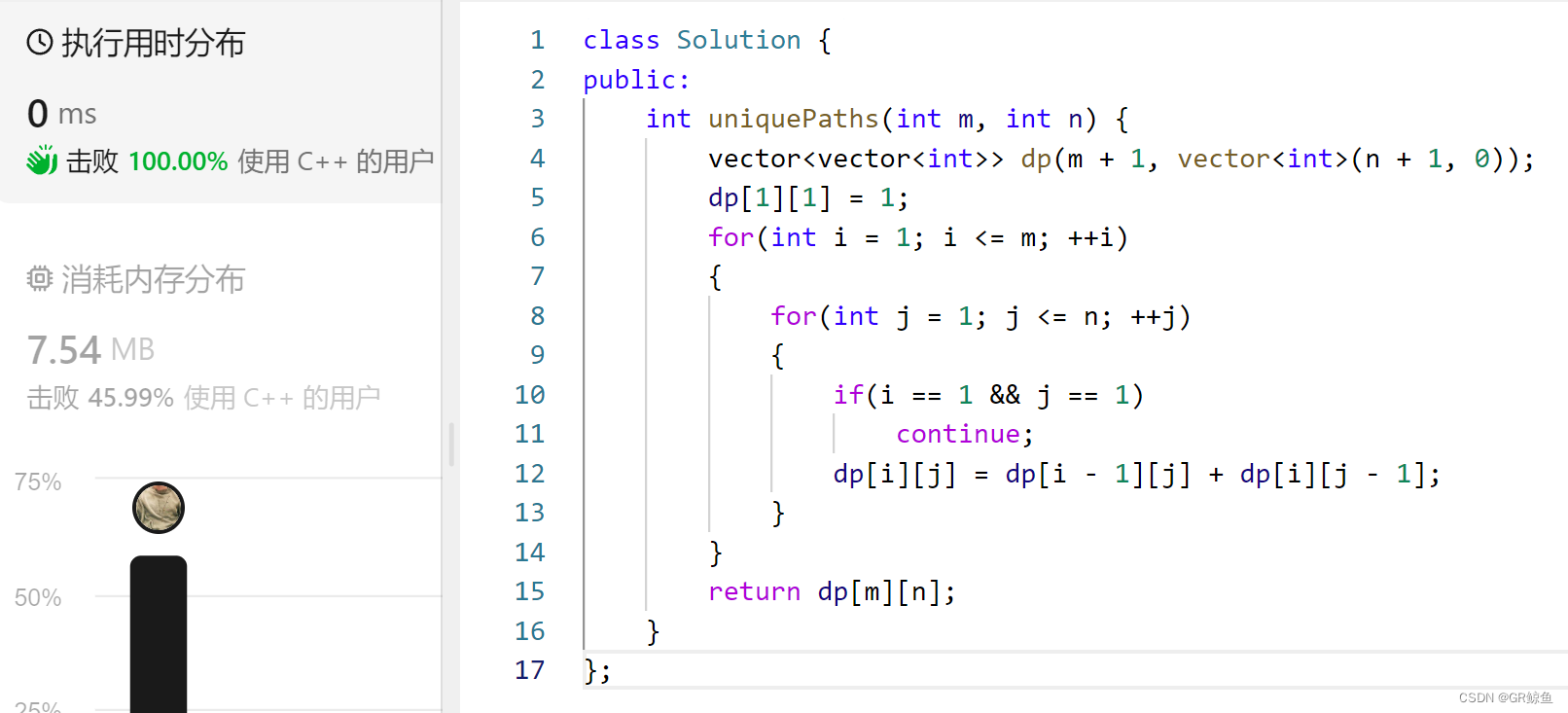
目录 力扣62. 不同路径 解析代码1_暴搜递归(超时) 解析代码2_记忆化搜索 解析代码3_动态规划 力扣62. 不同路径 62. 不同路径 难度 中等 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器…...
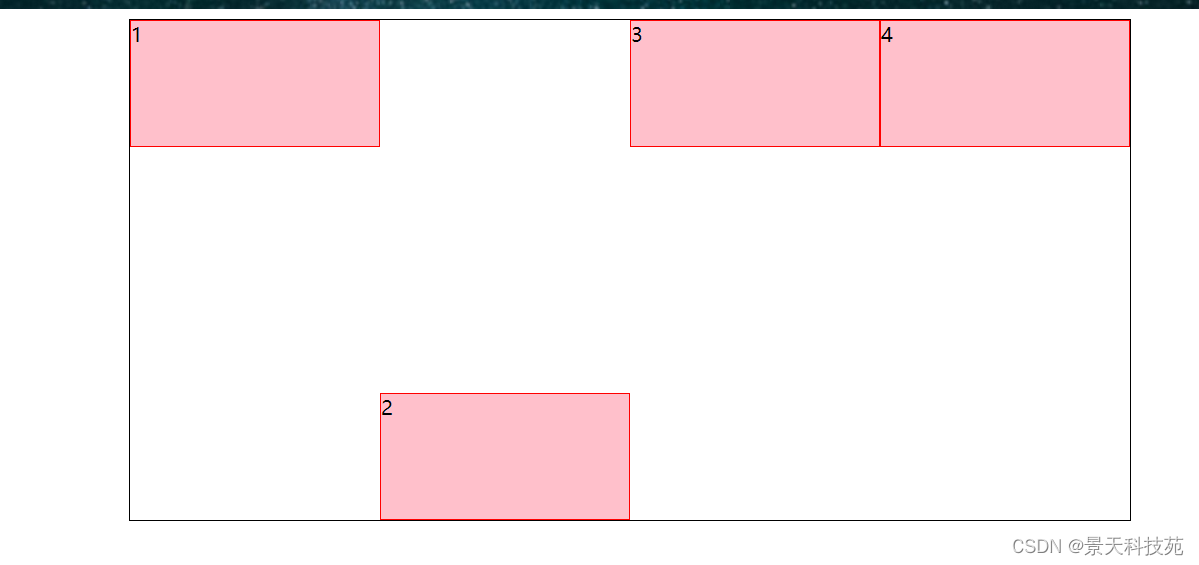
【微信小程序开发】微信小程序、大前端之flex布局方式详细解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
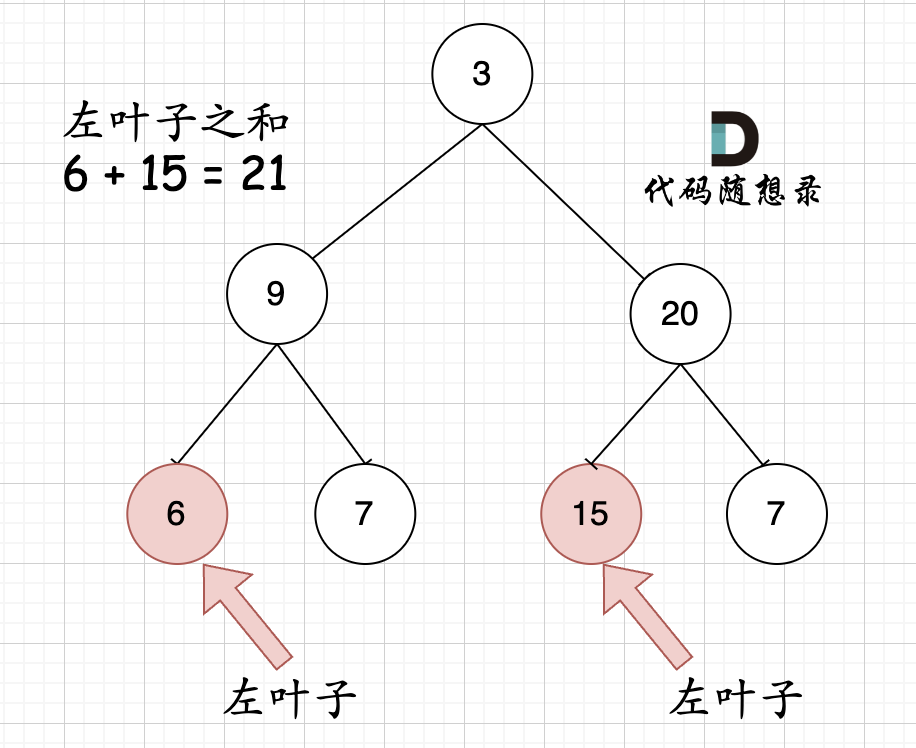
代码随想录算法训练营第二十天:二叉树成长
代码随想录算法训练营第二十天:二叉树成长 110.平衡二叉树 力扣题目链接(opens new window) 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝…...

Opensbi初始化分析:设备初始化-warmboot
Opensbi初始化分析:设备初始化-warmboot 设备初始化sbi_init函数init_warmboot函数coolboot & warmbootwait_for_coldboot函数domain && scratch(coldboot所特有)console初始化及print相关工作(coldboot所特有)系统调用的相关初始化(coldboot所特有)综上设备…...
)
软考 系统架构设计师系列知识点之软件可靠性基础知识(13)
接前一篇文章:软考 系统架构设计师系列知识点之软件可靠性基础知识(12) 所属章节: 第9章. 软件可靠性基础知识 第3节 软件可靠性管理 为了进一步提高软件可靠性,人们又提出了软件可靠性管理的概念,把软件可…...
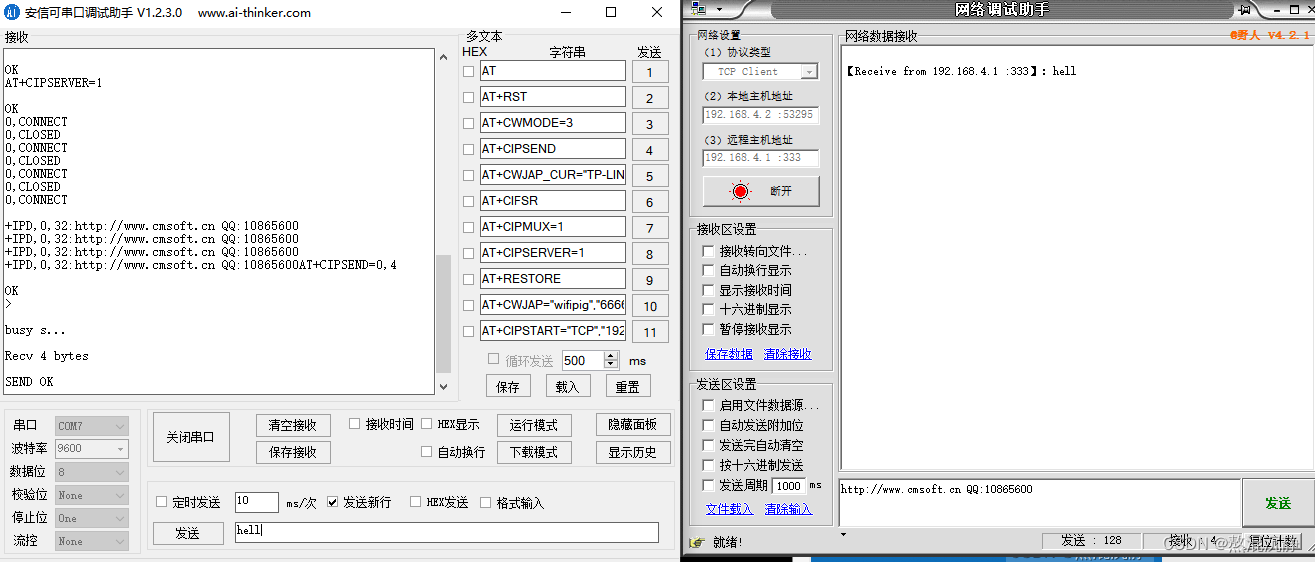
将ESP工作为AP路由模式并当成服务器
将ESP8266模块通过usb转串口接入电脑 ATCWMODE3 //1.配置成双模ATCIPMUX1 //2.使能多链接ATCIPSERVER1 //3.建立TCPServerATCIPSEND0,4 //4.发送4个字节在链接0通道上 >ATCIPCLOSE0 //5.断开连接通过wifi找到安信可的wifi信号并连接 连接后查看自己的ip地址变为192.168.4.…...
Python深度学习基于Tensorflow(6)神经网络基础
文章目录 使用Tensorflow解决XOR问题激活函数正向传播和反向传播解决过拟合权重正则化Dropout正则化批量正则化 BatchNormal权重初始化残差连接 选择优化算法传统梯度更新算法动量算法NAG算法AdaGrad算法RMSProp算法Adam算法如何选择优化算法 使用tf.keras构建神经网络使用Sequ…...

力扣HOT100 - 35. 搜索插入位置
解题思路: 二分法模板 class Solution {public int searchInsert(int[] nums, int target) {int left 0;int right nums.length - 1;while (left < right) {int mid left ((right - left) >> 1);if (nums[mid] target)return mid;else if (nums[mid…...
MinimogWP WordPress 主题下载——优雅至上,功能无限
无论你是个人博客写手、创意工作者还是企业站点的管理员,MinimogWP 都将成为你在 WordPress 平台上的理想之选。以其优雅、灵活和功能丰富而闻名,MinimogWP 不仅提供了令人惊叹的外观,还为你的网站带来了无限的创作和定制可能性。 无与伦比的…...
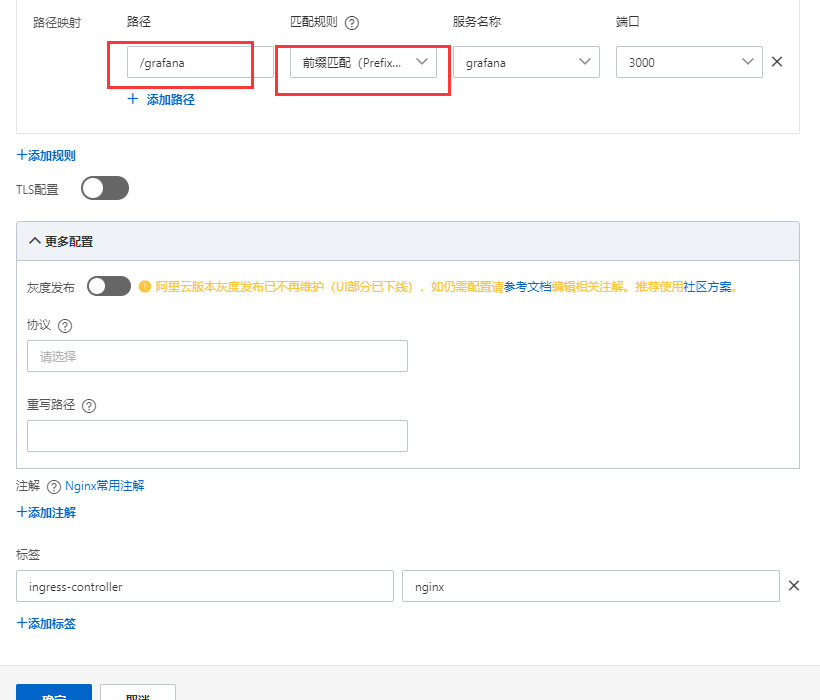
kube-prometheus部署到 k8s 集群
文章目录 **修改镜像地址****访问配置****修改 Prometheus 的 service****修改 Grafana 的 service****修改 Alertmanager 的 service****安装****Prometheus验证****Alertmanager验证****Grafana验证****卸载****Grafana显示时间问题** 或者配置ingress添加ingress访问grafana…...

从0开始学习python(六)
目录 前言 1、循环结构 1.1 遍历循环结构for 1.2 无限循环结构while 总结 前言 上一篇文章我们讲到了python的顺序结构和分支结构。这一章继续往下讲。 1、循环结构 在python中,循环结构分为两类,一类是遍历循环结构for,一类是无限循环结…...
OpenGL 入门(三)—— OpenGL 与 OpenCV 共同打造大眼滤镜
从本篇开始,会在上一篇搭建的滤镜框架的基础上,介绍具体的滤镜效果该如何制作。本篇会先介绍大眼滤镜,先来看一下效果,原图如下: 使用手机后置摄像头对眼部放大后的效果: 制作大眼滤镜所需的主要知识点&…...
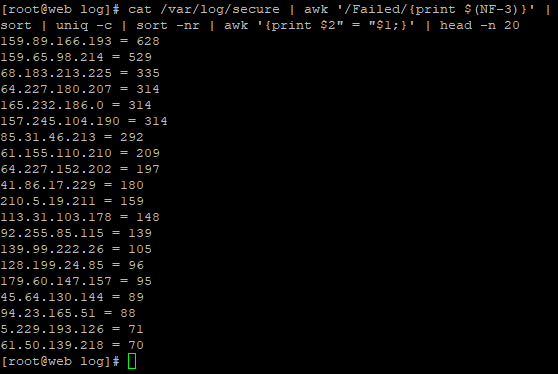
Linux服务器安全基础 - 查看入侵痕迹
1. 常见系统日志 /var/log/cron 记录了系统定时任务相关的日志 /var/log/dmesg 记录了系统在开机时内核自检的信息,也可以使用dmesg命令直接查看内核自检信息 /var/log/secure:记录登录系统存取数据的文件;例如:pop3,ssh,telnet,ftp等都会记录在此. /var/log/btmp:记…...

Java反射机制的实战应用:探索其魅力与局限
引言 Java作为一种面向对象的编程语言,其灵活性和强大的功能使其成为众多开发者的首选。而Java反射机制作为Java语言中的一项重要特性,为程序员提供了一种在运行时检查和操作类、方法、属性等信息的能力。本文旨在深入探讨Java反射机制的实战应用&#…...

vue3项目 文件组成
从头捋顺一遍vue3项目文件目录 前置知识JS模块化什么是依赖?安装依赖webpack能做什么?vue基本使用 不借助vue-cli,从0开始搭建vue项目。index.html、main.js、App.vue引入npm引入webpack引入babel引入vue-loaderwebpack配置webpack配置 前置知…...

C语言关键字 typedef 的功能是什么?
一、问题 语⾔有 32 个关键字,其中 int 的功能是声明整型变量,struct 的功能是声明结构体变量,那么 typedef 的功能是什么呢? 二、解答 1. typedef 的功能 在 C 语⾔中除了可以使⽤标准类型名(如 int、 char、float …...

【YoloDeployCsharp】基于.NET Framework的YOLO深度学习模型部署测试平台-源码下载与项目配置
基于.NET Framework 4.8 开发的深度学习模型部署测试平台,提供了YOLO框架的主流系列模型,包括YOLOv8~v9,以及其系列下的Det、Seg、Pose、Obb、Cls等应用场景,同时支持图像与视频检测。模型部署引擎使用的是OpenVINO™、TensorRT、ONNX runtime以及OpenCV DNN,支持CPU、IGP…...

如何在 Ubuntu 12.04 VPS 上使用 MongoDB 创建分片集群
简介 MongoDB 是一个 NoSQL 文档数据库系统,可以在水平方向上很好地扩展,并通过键值系统实现数据存储。作为 Web 应用程序和网站的热门选择,MongoDB 易于实现并可以通过编程方式访问。 MongoDB 通过一种称为“分片”的技术实现扩展。分片是将…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
