机器学习(二) ----------K近邻算法(KNN)+特征预处理+交叉验证网格搜索
目录
1 核心思想
1.1样本相似性
1.2欧氏距离(Euclidean Distance)
1.3其他距离
1.3.1 曼哈顿距离(Manhattan Distance)
1.3.2 切比雪夫距离(Chebyshev distance)
1.3.3 闵式距离(也称为闵可夫斯基距离,Minkowski Distance)
2 K值选择
2.1 K值的含义
2.2 K值的影响:
2.3 如何选择K值:
3 KNN解决问题流程
3.1 分类流程
3.2 回归流程
4 KNN算法的API
4.1 分类算法
4.2 回归算法
5 特征预处理(FeaturePreprocessing)(特征缩放)
5.1 归一化(Normalization)(Min-Max缩放)
5.1.1 归一化公式
5.1.2 归一化适用范围
5.1.3 归一化API
5.1.4 代码实现
5.2 标准化(Standardization)(Z-score标准化)
5.2.1 标准化公式
5.2.2 标准化的适用范围(常用)
5.2.3 数据标准化API
5.2.4 代码实现
6 交叉验证网格搜索(超参数选择)
6.1 交叉验证(Cross Validation):
6.2 网格搜索(GridSearch):
6.3 交叉验证网格搜索API
7 鸢尾花案例
1 核心思想
KNN(K-Nearest Neighbors)是一种基本的机器学习分类和回归算法。其核心思想是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
1.1样本相似性
样本都是属于一个任务数据集的,样本距离越近则越相似
1.2欧氏距离(Euclidean Distance)
欧氏距离(Euclidean Distance)是最常见的距离度量方式之一,用于在多维空间中计算两点之间的直线距离。
二维:a(x1,y1) b(x2,y2)
三维:a(x1,y1,z1) b(x2,y2,z2)
多维:a(x11,x12,....,x1n)b(x21,x22,....,x2n)
在机器学习和数据挖掘中,欧氏距离常用于KNN(K-Nearest Neighbors)等算法中,用于度量样本之间的相似性或距离。然而,需要注意的是,欧氏距离在处理高维数据时可能会受到“维数灾难”的影响,即在高维空间中,两点之间的欧氏距离可能会变得非常接近,导致算法的性能下降。此外,欧氏距离对数据的尺度敏感,因此在应用之前通常需要对数据进行标准化或归一化处理。
1.3其他距离
1.3.1 曼哈顿距离(Manhattan Distance)
曼哈顿距离的名字来源于规划为方型建筑区块的城市(如曼哈顿),其中从一个地点到另一个地点需要沿着街区行走,即只能沿着水平和垂直方向移动,而不能直接穿越建筑物。因此,曼哈顿距离可以理解为从一个点到另一个点在南北方向和东西方向上所走的距离之和。
公式:
a(x11,x12,....,x1n)b(x21,x22,....,x2n)
与欧氏距离相比,曼哈顿距离不受数据尺度的影响,因此在某些情况下可能更加合适。然而,曼哈顿距离对于数据的旋转和映射不敏感,即当坐标轴发生旋转或映射时,曼哈顿距离可能会发生变化。因此,在选择使用曼哈顿距离还是欧氏距离时,需要根据具体的应用场景和数据特点进行选择。
1.3.2 切比雪夫距离(Chebyshev distance)
切比雪夫距离得名自俄罗斯数学家切比雪夫。在二维空间中,和一点的切比雪夫距离为定值的点会形成一个正方形,而在更高维度的空间中,这些点会形成一个超立方体。
切比雪夫距离特别适用于多维空间中的距离测量,它通过定义最大坐标距离来衡量两点之间的“距离”,这在一些特殊应用中可能很有用,例如在国际象棋中,王从一个位置走到另一个位置需要的步数恰为两个位置之间的切比雪夫距离,因此切比雪夫距离也称为棋盘距离。
公式:
a(x11,x12,....,x1n)b(x21,x22,....,x2n)
1.3.3 闵式距离(也称为闵可夫斯基距离,Minkowski Distance)
闵式距离的特点是将各个分量的量纲,即“单位”当作相同看待,没有考虑各个量的分布(如期望、方差等)可能不同。
公式:
a(x11,x12,....,x1n)b(x21,x22,....,x2n)
2 K值选择
在KNN(K-Nearest Neighbors)算法中,K值的选择是一个重要的步骤,因为它直接影响到模型的性能。
2.1 K值的含义
K值表示在分类或回归时,我们要考虑的最近邻的数量。对于给定的测试点,KNN会找到训练数据集中与该点最近的K个点,然后根据这些点的标签进行投票(分类)或计算平均值(回归)
2.2 K值的影响:
K值较小时:模型复杂度较高,对噪声和异常值较敏感,可能导致过拟合。即,只有与测试点非常接近的少数几个点会影响分类或回归的结果。
K值较大时:模型复杂度较低,对噪声和异常值的敏感度降低,但可能导致欠拟合。即,即使与测试点不太接近的点也会对分类或回归的结果产生影响。
2.3 如何选择K值:
- 交叉验证:一种常用的方法是使用交叉验证来选择K值。具体来说,可以将训练数据集分成多个部分,然后对每个可能的K值进行训练和验证,选择使验证误差最小的K值。在交叉验证时,通常建议K值在2到20之间选择,并且最好为奇数,以避免出现平票的情况。
- 网格搜索:网格搜索(Grid Search)是一种在机器学习中常用的超参数优化方法,其原理是将待搜索的超参数空间划分为网格,然后遍历网格中的每一个点(即每一组超参数组合),通过交叉验证等方法评估每一组超参数组合的性能,并选择性能最优的一组作为最终的超参数设置。
- 经验法则:在实际应用中,有时候可以根据经验来选择K值。例如,在一些情况下,选择K=3、5或7可能会得到较好的结果。但是,这并不是绝对的,具体还需要根据数据集的特点和需求来确定。
- 贝叶斯优化:贝叶斯优化是一种高效的优化方法,可以用于在KNN算法中搜索最优的K值。它通过建模目标函数和先验分布,利用贝叶斯定理来更新参数分布,从而找到使目标函数最小化或最大化的最优参数。
3 KNN解决问题流程
3.1 分类流程
1.计算未知样本到每一个训练样本距离
2.将训练样本根据距离大小升序排列
3.取出距离最近的K个样本
4.进行多数表决,统计K个样本中哪个类别的样本个数最多
5.将未知的样本归属到出现次数最多的类别
3.2 回归流程
1.计算未知样本到每一个训练样本距离
2.将训练样本根据距离大小升序排列
3.取出距离最近的K个样本
4.计算这K个样本的目标值的平均值
5.将该平均值作为未知样本预测的值
4 KNN算法的API
4.1 分类算法
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)具体实现(此处仅做API距离,实际样本需要规模化):
# 导包
from sklearn.neighbors import KNeighborsClassifier# 实例化模型,设置K为3
Knn = KNeighborsClassifier(n_neighbors=3)# 准备数据X为特征向量空间,y为标签值
X = [[0, 1], [5, 1], [9, 8], [4, 8], [9, 7], [3, 8], [7, 66], [4, 8], [3, 2], [7, 9]]
y = [1, 0, 1, 0, 1, 0, 1, 0, 0, 1]# 训练模型
Knn.fit(X, y)# 预测
print(Knn.predict([[9, 9]]))4.2 回归算法
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5)具体实现(此处仅做API距离,实际样本需要规模化):
from sklearn.neighbors import KNeighborsRegressor# 实例化模型
Knn = KNeighborsRegressor(n_neighbors=3)
# 准备数据
X = [[0, 1], [5, 1], [9, 8], [4, 8], [9, 7], [3, 8], [7, 66], [4, 8], [3, 2], [7, 9]]
y = [1, 2, 34, 2, 6, 56, 8, 9, 0, 9]# 训练模型
Knn.fit(X, y)# 预测
print(Knn.predict([[9, 9], [0, 7]]))5 特征预处理(FeaturePreprocessing)(特征缩放)
将不同尺度的特征缩放到相似的范围,以避免某些特征对模型的影响过大。常见的特征缩放方法有标准化(Z-score标准化)和归一化(Min-Max缩放)。
5.1 归一化(Normalization)(Min-Max缩放)
归一化(Normalization)是数据预处理中常用的一种技术,它可以将数据的尺度调整到某个特定的范围[mi,ma],通常是[0, 1]或[-1, 1]。归一化的主要目的是消除数据之间的尺度差异,使得不同特征之间具有相似的权重,从而提高模型的稳定性和准确性。
5.1.1 归一化公式
min为特征的最小值,max为特征的最大值
mx为特定范围的上界,mi为特定范围的下界
5.1.2 归一化适用范围
如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
应用场景:
最大值好最小值非常容易受异常点影响,只适合传统精确小数据场景,如图像处理时的像素值
5.1.3 归一化API
# 实例化
transfor = sklearn.preprocessing.MinMaxScaler(feature_range = (0,1))
# 归一化
transfor.transform(X)5.1.4 代码实现
# 归一化
# 导包
from sklearn.preprocessing import MinMaxScaler# 准备数据
data = [[90, 60, 1], [60, 257, 3], [20, 1, 6]]# 实例化
transform = MinMaxScaler()# 归一化
print(transform.fit_transform(data))5.2 标准化(Standardization)(Z-score标准化)
标准化(Standardization)是一种常见的数据预处理技术,其主要目的是通过调整数据的尺度,使其具有零均值和单位方差,从而使数据更符合标准正态分布。
5.2.1 标准化公式
mean为特征的平均值 σ为特征的标准差
5.2.2 标准化的适用范围(常用)
如果出现异常点,由于少量的异常点对于平均值和方差影响不大,所以适合现代嘈杂大数据场景
5.2.3 数据标准化API
# 实例化
transfor = sklearn.preprocessing.Standard()
# 标准化
transfor.fit_transform(X)5.2.4 代码实现
# 标准化
# 导包
from sklearn.preprocessing import StandardScaler# 准备数据
data = [[90, 60, 1], [60, 257, 3], [20, 1, 6]]# 实例化
transform = StandardScaler()# 标准化
print(transform.fit_transform(data))
print(transform.var_)
print(transform.mean_)6 交叉验证网格搜索(超参数选择)
6.1 交叉验证(Cross Validation):
交叉验证是一种评估机器学习模型性能的统计学方法。其主要目的是通过对训练集进行多次划分,得到不同的训练集和验证集组合,然后分别在这些组合上训练模型并验证其性能,从而得到对模型性能的更加准确和可靠的评估。
K折交叉验证(K-fold Cross Validation):将原始数据分为K份,然后每次选择K-1份作为训练集,剩下的1份作为验证集。这样重复K次,每次选择不同的验证集。最后取K次验证结果的平均值作为最终评估结果。这种方法可以有效减少随机性对评估结果的影响。
6.1.1 交叉验证步骤
1.将数据集换分为cv=k份
2.第一次:把第一份数据做验证集,其余数据作训练
3.第二次:把第二份数据做验证集,其余数据做训练
4.....以此类推,总共训练k次,评估k次
5.使用训练集+验证集多次评估模型,取平均值做交叉验证的模型得分
6.若超参数组合(n1,n2,...)模型得分最好,再使用全部训练集(训练集+验证集)对超参数组合(n1,n2,...)模型再训练(此步骤在交叉验证网格搜索API里已经执行完,不必重新执行)
7.在使用测试集对该模型进行评估
6.2 网格搜索(GridSearch):
网格搜索是一种用于优化机器学习模型超参数的搜索方法。在机器学习中,许多模型的性能会受到一些参数的影响,这些参数称为超参数(Hyperparameters)。手动调整这些超参数的过程通常很繁琐,而且很难找到最优的参数组合。网格搜索通过预设一组超参数组合,然后对每个组合进行交叉验证评估,最后选择性能最好的参数组合作为最优参数组合。这种方法可以大大简化超参数的调整过程,并且可以找到相对较好的参数组合。
在网格搜索中,通常会使用估计器(Estimator)对象来表示模型,并使用param_grid参数来指定要搜索的超参数组合范围。然后,通过调用fit()方法输入训练数据,并使用score()方法获取每个参数组合的交叉验证结果。最后,根据这些结果选择最优的参数组合,并使用best_params_、best_score_等属性获取最优参数和最优结果。
6.3 交叉验证网格搜索API
# 实例化
estimator = sklearn.model_selection.GridSearchCV(estimater,param_grid=None,cv=None)# 交叉验证
estimator.fit(x_trian,y_train)
参数解释:
estimator:估计器对象(实例化模型)
param_grid:估计器参数(dict){‘n_neighbors’:[5,7,9,11]}
cv:指定几折交叉验证(将测试集分成几部分进行交叉验证)
结果分析:
estimator.best_score_ 在交叉验证中验证的最好结果
estimator.beat_estimator_ 最好的参数模型
estimator.beat_params_ 最好的超参数组合
estimator.cv_results_ 交叉验证结果
7 鸢尾花案例
# 1.导包
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier# 2.加载数据
data_iris = load_iris()
# 3.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data_iris.data, data_iris.target, train_size=0.8, random_state=17)# 4.特征预处理-标准化
transfor = StandardScaler()
x_train = transfor.fit_transform(x_train)
x_test = transfor.transform(x_test)
# 5.模型实例化
knn = KNeighborsClassifier()# 6.网格搜索交叉验证
estimater = GridSearchCV(estimator=knn, param_grid={'n_neighbors': [1, 3, 5, 7, 9]}, cv=6)
estimater.fit(x_train, y_train)
print(estimater.best_estimator_)
print(estimater.best_index_)
print(estimater.best_params_)
print(estimater.best_score_)
print(estimater.cv_results_)# 7.评估print(estimater.score(x_test, y_test))# 8.预测pre = [[1, 1, 1, 1], [2, 3, 2, 2]]
pre = transfor.transform(pre)
print(estimater.predict(pre))
KNN算法简单直观,易于理解和实现,并且不需要进行模型训练(即没有显式的训练过程)。然而,KNN算法的计算复杂度较高,特别是对于大型数据集,因为需要计算每个新数据点与所有已知数据点之间的距离。此外,KNN算法对数据的标准化和缩放等预处理步骤较为敏感,因为距离度量是基于特征空间中的数值大小。尽管如此,KNN算法仍然是机器学习领域中的一个重要工具,广泛应用于各种实际问题和场景中。
相关文章:
机器学习(二) ----------K近邻算法(KNN)+特征预处理+交叉验证网格搜索
目录 1 核心思想 1.1样本相似性 1.2欧氏距离(Euclidean Distance) 1.3其他距离 1.3.1 曼哈顿距离(Manhattan Distance) 1.3.2 切比雪夫距离(Chebyshev distance) 1.3.3 闵式距离(也称为闵…...

This error originates from a subprocess, and is likely not a problem with pip.
Preparing metadata (setup.py) ... errorerror: subprocess-exited-with-error python setup.py egg_info did not run successfully.│ exit code: 1╰─> [63 lines of output]WARNING: The repository located at mirrors.aliyun.com is not a trusted or secure host a…...

Python中关于子类约束的开发规范
Python中关于子类约束的开发规范 我们知道,在java和C#中有一种接口的类型,用来约束实现该接口的类,必须要定义接口中指定的方法 而在python中,我们可以基于父类子类异常来仿照着实现这个功能 class Base:def func():raise NotI…...
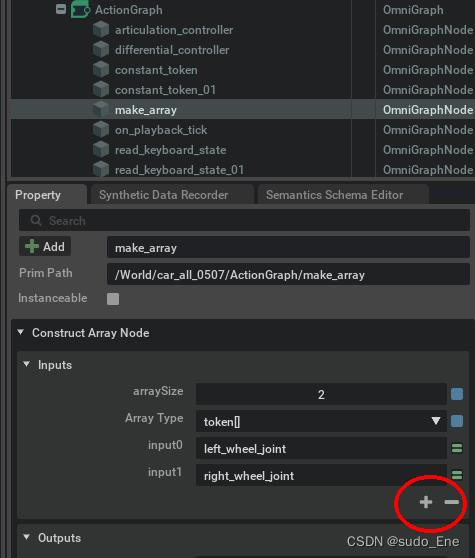
Isaac Sim 4 键盘控制小车前进方向(学习笔记5.8.2)
写的乱糟糟,主要是这两周忘了记录了...吭哧吭哧往下搞,突然想起来要留档,先大致写一个,后面再往里添加和修改吧,再不写就全忘了 有一个一直没解决的问题: 在保存文件时出现问题:isaac sim mism…...
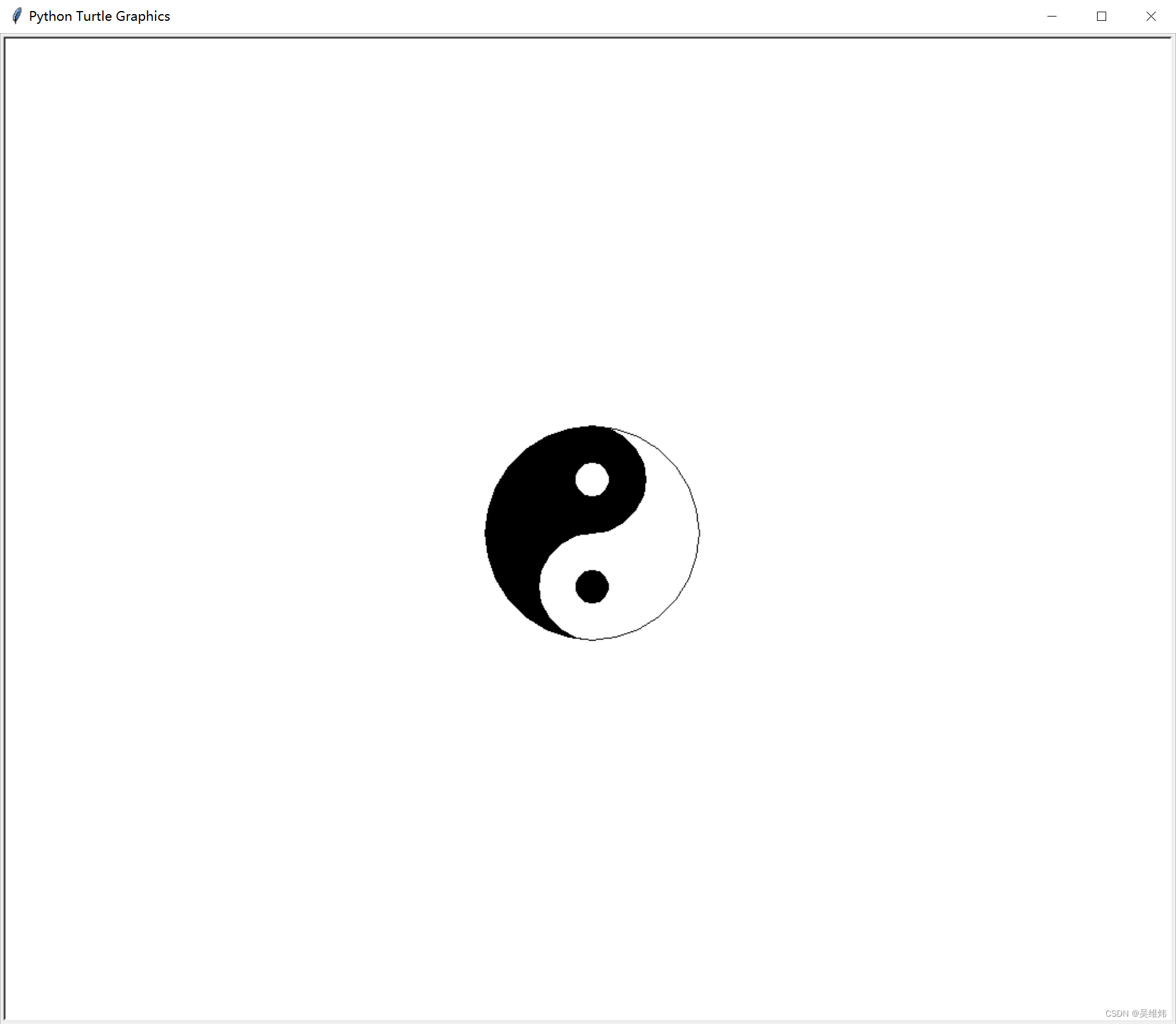
「Python绘图」绘制太极图
python 绘制太极 一、预期结果 二、核心代码 import turtlepen turtle.Turtle()print("开始绘制太极")radius 100 pen.color("black", "black") pen.begin_fill() pen.circle(radius/2, 180) pen.circle(radius, 180) pen.left(180) pen.circ…...
解决html2canvas生成图片慢的问题
// 主要看那个点击事件就行 <divclass"textBox-right-board-group"v-for"item in screenList":key"item.id"><!-- 获取不同分辨率下的屏幕的展示的文字大小DPI: fontSize: getFontSize(item.resolutionRatio), --><di…...
模型智能体开发之metagpt-多智能体实践
参考: metagpt环境配置参考模型智能体开发之metagpt-单智能体实践 需求分析 之前有过单智能体的测试case,但是现实生活场景是很复杂的,所以单智能体远远不能满足我们的诉求,所以仍然还需要了解多智能体的实现。通过多个role对动…...

Java | Leetcode Java题解之第67题二进制求和
题目: 题解: class Solution {public String addBinary(String a, String b) {StringBuffer ans new StringBuffer();int n Math.max(a.length(), b.length()), carry 0;for (int i 0; i < n; i) {carry i < a.length() ? (a.charAt(a.leng…...

考过PMP之后,为什么建议学CSPM?
在项目管理领域,PMP证书和CSPM证书都是非常重要的认证,那么CSPM到底是什么?含金量如何?为什么建议学习CSPM?今天,我们一起来了解CSPM! CSPM是什么? CSPM中文全称:项目管理专业人员…...

智能合约是什么?搭建与解析
智能合约是一种基于区块链技术的自动化执行合约,它通过编程语言编写,并在区块链网络上部署运行。智能合约是区块链技术的重要组成部分,它使得去中心化应用(DApp)的开发变得更加便捷和高效。本文将从智能合约的搭建、原…...
windows下安装最新的nginx
1、进入官网下载地址 https://nginx.org/en/download.html#/ 2、点击这里最新的版本下载 3、(不要直接运行解压的nginx.exe),应这样操作WindowsR,输入CMD, 4、查看一下自己解压后的位置,我的是在E盘 5、输入对应的W…...
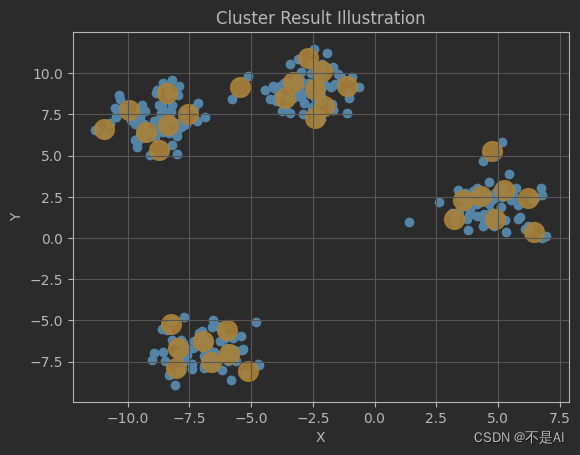
【深耕 Python】Data Science with Python 数据科学(19)书402页练习题:模型准确率对比研究、KMeans算法的一点探讨
写在前面 关于数据科学环境的建立,可以参考我的博客: 【深耕 Python】Data Science with Python 数据科学(1)环境搭建 往期数据科学博文一览: 【深耕 Python】Data Science with Python 数据科学(2&…...

汽车品牌区域营销方案
领克汽车粤海区域营销方案-36P 活动策划信息: 方案页码:36页 文件格式:PPT 方案简介: 车市反弹形势明显,领克销量呈现稳健上涨趋势 品牌 未来市场可观,应 持续扩大品牌声量,保持市场占有优…...

matlab 中在3维坐标系中绘制一个点的X,Y,Z坐标,除了mesh还有什么函数?使用格式与mesh都有什么区别?
在MATLAB中,除了mesh函数之外,还有其他一些函数可以用来在三维坐标系中绘制点或曲面。以下是一些常用的函数及其与mesh函数的区别: 函数名描述与mesh的区别plot3在三维坐标系中绘制线或点仅限于线或点的绘制,不生成网格scatter3在…...
如何在六个月内学会任何一门外语(ted转述)
/仅作学习和参考,勿作他用/ a question : how can you speed up learning? 学得快,减少在学校时间 结果去研究心理学惹 spend less time at school. if you learn really fast , you donot need to go to school at all. school got in the way of …...
前端 Android App 上架详细流程 (Android App)
1、准备上架所需要的材料 先在需要上架的官方网站注册账号。提前把手机号,名字,身份证等等材料准备好,完成开发者实名认证;软著是必要的,提前准备好,软著申请时间比较长大概需要1-2周时间才能下来…...
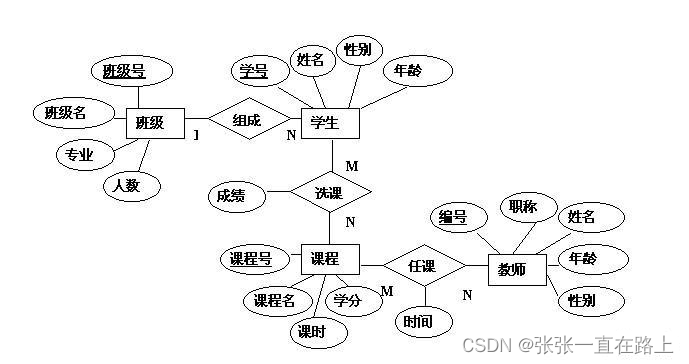
MySQL学习笔记11——数据备份 范式 ER模型
数据备份 & 范式 & ER模型 一、数据备份1、如何进行数据备份(1)备份数据库中的表(2)备份数据库(3)备份整个数据库服务器 2、如何进行数据恢复3、如何导出和导入表里的数据(1)…...
软件测试基础理论复习
什么是软件? 软件是计算机系统中与硬件相互依存的另一部分, 软件包括程序文档 什么是软件测试? (1)软件测试是在现有软件(程序文档)中寻找缺陷的过程; (2࿰…...

【UnityRPG游戏制作】Unity_RPG项目_玩家逻辑相关
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:就业…...

QT_BEGIN_NAMESPACE
最近碰到了QT_BEGIN_NAMESPACE这个宏,这个宏就是一个命名空间,意思是如果不用这个宏,可能我qwidget定义的一个变量a会和标准C定义的变量a冲突对不,Qt通过这个命名空间,将所有类和函数封装在一个作用域里,防…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
