计算方法实验9:Romberg积分求解速度、位移
任务

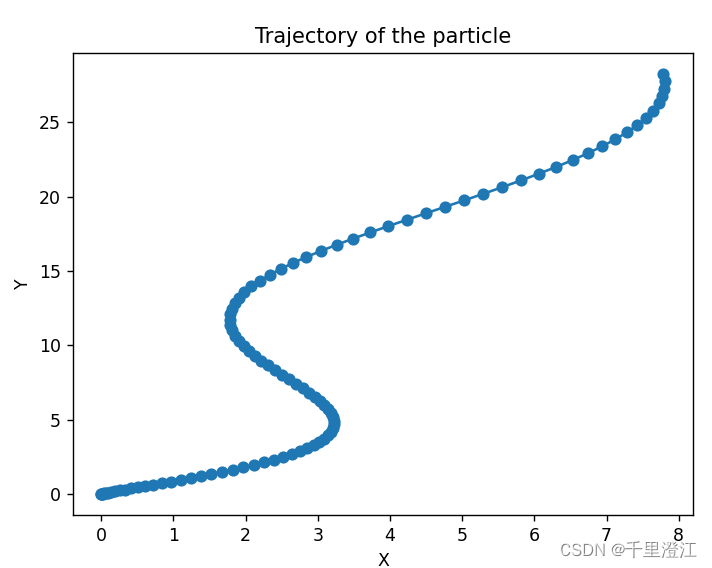
- 输出质点的轨迹 ( x ( t ) , y ( t ) ) , t ∈ { 0.1 , 0.2 , 0.3 , . . . , 10 } (x(t), y(t)), t\in \{0.1, 0.2, 0.3, ..., 10\} (x(t),y(t)),t∈{0.1,0.2,0.3,...,10},并在二维平面中画出该轨迹.
- 请比较M分别取4, 8, 12, 16, 20 时,Romberg积分达到要求精度的比例(达到误差要求的次数/调用总次数),分析该比例随M 的变化。
算法
现在要用数值方法求 ∫ a b f ( x ) d x \int_{a}^{b} f(x) \, dx ∫abf(x)dx,设 h = b − a n h=\frac{b-a}{n} h=nb−a,已知:
复化梯形积分 T n ( f ) = h [ 1 2 f ( a ) + ∑ i = 1 n − 1 f ( a + i h ) + 1 2 f ( b ) ] T_{n}\left(f\right)=h\left[\frac{1}{2}f\left(a\right)+\sum_{i=1}^{n-1}f\left(a+ih\right)+\frac{1}{2}f\left(b\right)\right] Tn(f)=h[21f(a)+∑i=1n−1f(a+ih)+21f(b)]、
复化Simpson积分 S n ( f ) = h 3 [ f ( a ) + 4 ∑ i = 0 m − 1 f ( x 2 i + 1 ) + 2 ∑ i = 1 m − 1 f ( x 2 i ) + f ( b ) ] S_{n}\left(f\right)=\frac{h}{3}\left[f\left(a\right)+4\sum_{i=0}^{m-1}f\left(x_{2i+1}\right)+2\sum_{i=1}^{m-1}f\left(x_{2i}\right)+f\left(b\right)\right] Sn(f)=3h[f(a)+4∑i=0m−1f(x2i+1)+2∑i=1m−1f(x2i)+f(b)].
将 ( T n ( f ) − T 2 n ( f ) ) ( T_n( f) - T_{2n}( f) ) (Tn(f)−T2n(f)) 作 为 T 2 n ( f ) T_{2n}(f) T2n(f)的修正值补充到 I ( f ) I(f) I(f),即
I ( f ) ≈ T 2 n ( f ) + 1 3 ( T 2 n ( f ) − T n ( f ) ) = 4 3 T 2 n − 1 3 T n = S n I(f)\approx T_{2n}(f)+\frac{1}{3}\left(T_{2n}\left(f\right)-T_{n}\left(f\right)\right)=\frac{4}{3}T_{2n}-\frac{1}{3}T_{n}=S_{n} I(f)≈T2n(f)+31(T2n(f)−Tn(f))=34T2n−31Tn=Sn
其结果是将复化梯形求积公式组合成复化 Simpson 求积公式, 截断误差由 O ( h 2 ) O(h^2) O(h2)提高到 O ( h 4 ) O(h^4) O(h4),这种手段称为外推算法,该算法在不增加计算量的前提下提高了误差的精度.不妨对 S 2 n ( f ) , S n ( f ) S_{2n}(f),S_n(f) S2n(f),Sn(f)再作一次线性组合:
I ( f ) − S n ( f ) = − f ( 4 ) ( ξ ) 180 h 4 ( b − a ) ≈ d h 4 I\left(f\right)-S_{n}\left(f\right)=-\frac{f^{\left(4\right)}\left(\xi\right)}{180}h^{4}\left(b-a\right)\approx dh^{4} I(f)−Sn(f)=−180f(4)(ξ)h4(b−a)≈dh4
I ( f ) − S 2 n ( f ) = − f ( 4 ) ( η ) 180 ( h 2 ) 4 ( b − a ) ≈ d ( h 2 ) 4 I(f)-S_{2n}(f)=-\frac{f^{(4)}(\eta)}{180}\left(\frac{h}{2}\right)^{4}(b-a)\approx d\left(\frac{h}{2}\right)^{4} I(f)−S2n(f)=−180f(4)(η)(2h)4(b−a)≈d(2h)4
I ( f ) ≈ S 2 n ( f ) + 1 15 ( S 2 n ( f ) − S n ( f ) ) = C n ( f ) I\left(f\right)\approx S_{2n}\left(f\right)+\frac{1}{15}\left(S_{2n}\left(f\right)-S_{n}\left(f\right)\right)=C_{n}\left(f\right) I(f)≈S2n(f)+151(S2n(f)−Sn(f))=Cn(f)
复化 Simpson 公式组成复化 Cotes 公式,其截断误差是 O ( h 6 ) . O(h^6). O(h6).同理对 Cotes公式进行线性组合:
I ( f ) − C 2 n ( f ) = e ( h 2 ) 6 I ( f ) − C n ( f ) = e h 6 I\left(f\right)-C_{2n}\left(f\right)=e\left(\frac{h}{2}\right)^{6}\\I\left(f\right)-C_{n}\left(f\right)=eh^{6} I(f)−C2n(f)=e(2h)6I(f)−Cn(f)=eh6
得到具有 7 次代数精度和截断误差是 O ( h 8 ) O(h^8) O(h8)的 Romberg 公式:
R n ( f ) = C 2 n ( f ) + 1 63 ( C 2 n ( f ) − C n ( f ) ) R_{n}\left(f\right)=C_{2n}\left(f\right)+\frac{1}{63}\left(C_{2n}\left(f\right)-C_{n}\left(f\right)\right) Rn(f)=C2n(f)+631(C2n(f)−Cn(f))
为了便于在计算机上实现 Romberg 算法,将 T n , S n , C n , R n , ⋯ T_n,S_n,C_n,R_n,\cdots Tn,Sn,Cn,Rn,⋯统一用 R k , j R_{k,j} Rk,j 表示,列标 j = 1 , 2 , 3 , 4 j=1,2,3,4 j=1,2,3,4分别表示梯形、Simpson、Cotes 、Romberg积分,行标 k k k表示步长 h k = h 2 k − 1 h_k=\frac h{2^{k-1}} hk=2k−1h,得到Romberg 计算公式:
R k , j = R k , j − 1 + R k , j − 1 − R k − 1 , j − 1 4 j − 1 − 1 , k = 2 , 3 , ⋯ R_{k,j}=R_{k,j-1}+\frac{R_{k,j-1}-R_{k-1,j-1}}{4^{j-1}-1},k=2,3,\cdots Rk,j=Rk,j−1+4j−1−1Rk,j−1−Rk−1,j−1,k=2,3,⋯
对每一个 k , j k,j k,j从 2 做到 k k k,一直做到 ∣ R k , k − R k − 1 , k − 1 ∣ |R_k,k-R_{k-1,k-1}| ∣Rk,k−Rk−1,k−1∣小于给定控制精度时停止计算.
注:下面代码中数组下标从0开始.
代码
C++实现Romberg积分运算
#include<bits/stdc++.h>
using namespace std;int satisfiedCount;long double ax(long double t);
long double ay(long double t);
long double romberg(function<long double(long double)> f, long double a, long double b, long double eps, int maxIter, bool isX);// Perform the Romberg integrationint main()
{long double eps = 1e-6, proportion;int maxIter;satisfiedCount = 0;maxIter = 4;cout << "maxIter = " << maxIter << endl;for (long double t = 0.1; t <= 10; t += 0.1) { long double vx = romberg(ax, 0, t, eps, maxIter, 0);long double vy = romberg(ay, 0, t, eps, maxIter, 0);long double x = romberg([&](long double t) { return vx; }, 0, t, eps, maxIter, 1);long double y = romberg([&](long double t) { return vy; }, 0, t, eps, maxIter, 0);cout << fixed << setprecision(1) << "At t = " << t << ", vx = " << setprecision(6) << vx << ", vy = " << setprecision(6) << vy << ", " << "(x, y) = (" << setprecision(6) << x << ", " << setprecision(6) << y << ")" << endl;}proportion = (long double)satisfiedCount / 100;cout << "At maxIter = " << maxIter << ", proportion of times the error requirement of x was satisfied: " << proportion << endl;satisfiedCount = 0;maxIter = 8;cout << "maxIter = " << maxIter << endl;ofstream outFile("trajectory.txt");for (long double t = 0.1; t <= 10; t += 0.1) {long double vx = romberg(ax, 0, t, eps, maxIter, 0);long double vy = romberg(ay, 0, t, eps, maxIter, 0);long double x = romberg([&](long double t) { return vx; }, 0, t, eps, maxIter, 1);long double y = romberg([&](long double t) { return vy; }, 0, t, eps, maxIter, 0);cout << fixed << setprecision(1) << "At t = " << t << ", vx = " << setprecision(6) << vx << ", vy = " << setprecision(6) << vy << ", " << "(x, y) = (" << setprecision(6) << x << ", " << setprecision(6) << y << ")" << endl;outFile << fixed << setprecision(6) << x << " " << y << "\n";//把坐标写入文件,方便画轨迹}proportion = (long double)satisfiedCount / 100;cout << "At maxIter = " << maxIter << ", proportion of times the error requirement of x was satisfied: " << proportion << endl;satisfiedCount = 0;maxIter = 12;cout << "maxIter = " << maxIter << endl;for (long double t = 0.1; t <= 10; t += 0.1) {long double vx = romberg(ax, 0, t, eps, maxIter, 0);long double vy = romberg(ay, 0, t, eps, maxIter, 0);long double x = romberg([&](long double t) { return vx; }, 0, t, eps, maxIter, 1);long double y = romberg([&](long double t) { return vy; }, 0, t, eps, maxIter, 0);cout << fixed << setprecision(1) << "At t = " << t << ", vx = " << setprecision(6) << vx << ", vy = " << setprecision(6) << vy << ", " << "(x, y) = (" << setprecision(6) << x << ", " << setprecision(6) << y << ")" << endl;}proportion = (long double)satisfiedCount / 100;cout << "At maxIter = " << maxIter << ", proportion of times the error requirement of x was satisfied: " << proportion << endl;satisfiedCount = 0;maxIter = 16;cout << "maxIter = " << maxIter << endl;for (long double t = 0.1; t <= 10; t += 0.1) {long double vx = romberg(ax, 0, t, eps, maxIter, 0);long double vy = romberg(ay, 0, t, eps, maxIter, 0);long double x = romberg([&](long double t) { return vx; }, 0, t, eps, maxIter, 1);long double y = romberg([&](long double t) { return vy; }, 0, t, eps, maxIter, 0);cout << fixed << setprecision(1) << "At t = " << t << ", vx = " << setprecision(6) << vx << ", vy = " << setprecision(6) << vy << ", " << "(x, y) = (" << setprecision(6) << x << ", " << setprecision(6) << y << ")" << endl;}proportion = (long double)satisfiedCount / 100;cout << "At maxIter = " << maxIter << ", proportion of times the error requirement of x was satisfied: " << proportion << endl;satisfiedCount = 0;maxIter = 20;cout << "maxIter = " << maxIter << endl;for (long double t = 0.1; t < 10.1; t += 0.1) {long double vx = romberg(ax, 0, t, eps, maxIter, 0);long double vy = romberg(ay, 0, t, eps, maxIter, 0);long double x = romberg([&](long double t) { return vx; }, 0, t, eps, maxIter, 1);long double y = romberg([&](long double t) { return vy; }, 0, t, eps, maxIter, 0);cout << fixed << setprecision(1) << "At t = " << t << ", vx = " << setprecision(6) << vx << ", vy = " << setprecision(6) << vy << ", " << "(x, y) = (" << setprecision(6) << x << ", " << setprecision(6) << y << ")" << endl;}proportion = (long double)satisfiedCount / 100;cout << "At maxIter = " << maxIter << ", proportion of times the error requirement of x was satisfied: " << proportion << endl;return 0;
}long double ax(long double t)
{return sin(t) / (1 + sqrt(t));
}long double ay(long double t)
{return log(t + 1) / (t + 1);
}// Perform the Romberg integration
long double romberg(function<long double(long double)> f, long double a, long double b, long double eps, int maxIter, bool isX) {long double h[maxIter], r[maxIter][maxIter];h[0] = b - a;r[0][0] = 0.5 * h[0] * (f(a) + f(b));for (int i = 1; i < maxIter; i++) {h[i] = 0.5 * h[i-1];long double sum = 0;for (int k = 0; k < pow(2, i-1); k++)sum += f(a + (2*k+1) * h[i]);r[i][0] = 0.5 * r[i-1][0] + h[i] * sum;for (int j = 1; j <= i; j++)r[i][j] = r[i][j-1] + (r[i][j-1] - r[i-1][j-1]) / (pow(4, j) - 1);if (i > 1 && fabs(r[i][i] - r[i-1][i-1]) < eps){if(isX)satisfiedCount++;return r[i][i];}}return r[maxIter-1][maxIter-1];
}
python可视化运动轨迹
import matplotlib.pyplot as pltwith open('trajectory.txt', 'r') as file:lines = file.readlines()x, y = zip(*[(float(line.split()[0]), float(line.split()[1])) for line in lines])plt.plot(x, y, 'o-')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Plot of points with smooth curve')
plt.show()
结果
部分运算结果

轨迹可视化结果
相关文章:

计算方法实验9:Romberg积分求解速度、位移
任务 输出质点的轨迹 ( x ( t ) , y ( t ) ) , t ∈ { 0.1 , 0.2 , 0.3 , . . . , 10 } (x(t), y(t)), t\in \{0.1, 0.2, 0.3, ..., 10\} (x(t),y(t)),t∈{0.1,0.2,0.3,...,10},并在二维平面中画出该轨迹.请比较M分别取4, 8, 12, 16, 20 时,Romberg积分达…...

设计模式有哪些基本原则
目录 开闭原则(Open Closed Principle) 里氏替换原则(Liskov Substitution principle) 单一职责原则(Single Responsibility Principle,SRP)...
别再出错了!华为交换机到底如何配置access、trunk、hybird端口?
号主:老杨丨11年资深网络工程师,更多网工提升干货,请关注公众号:网络工程师俱乐部 下午好,我的网工朋友。 我们都知道,网络工程师的工作离不开对交换机的熟练操作。华为交换机的配置,绝对是考验…...

OceanBase 分布式数据库【信创/国产化】- OceanBase 平台产品 - 迁移评估工具 OMA
本心、输入输出、结果 文章目录 OceanBase 分布式数据库【信创/国产化】- OceanBase 平台产品 - 迁移评估工具 OMA前言OceanBase 数据更新架构OceanBase 平台产品 - 迁移评估工具 OMA兼容性评估性能评估导出 OceanBase 数据库对象和 SQL 语句OceanBase 分布式数据库【信创/国产…...
UE5入门学习笔记(六)——编译低版本插件
对于有些低版本的插件,可以通过此方法自己编译到高版本而无需等待插件作者更新 使用工具:如图所示 步骤1:打开cmd,并使用cd命令切换到此目录 步骤2:输入如下指令 RunUAT.bat BuildPlugin -Plugin“路径1” -Package“…...

MySQL全局锁、表级锁、行锁、死锁、索引选择
文章目录 全局锁表级锁表锁元数据锁 MDL 如何安全的给小表添加字段1. 理解和监控长事务2. 使用NOWAIT和WAIT语法示例 3. 选择合适的时间窗口4. 分阶段执行5. 使用在线DDL工具 行锁死锁普通索引和唯一索引的选择索引基础业务场景分析性能考量实践建议索引及其选择机制索引选择错…...

深入解析算法效率核心:时间与空间复杂度概览及优化策略
算法复杂度,即时间复杂度与空间复杂度,衡量算法运行时资源消耗。时间复杂度反映执行时间随数据规模增长的关系,空间复杂度表明额外内存需求。优化策略,如选择合适数据结构、算法改进、循环展开等,对于提升程序效率、减…...
虚拟机装CentOS镜像
起先,是先安装一个VM虚拟机,再去官方网站之类的下载一些镜像,常见镜像有CentOS镜像,ubantu镜像,好像还有一个树莓还是什么的,软件这块,日新月异,更新太快,好久没碰&#…...
SpringCloud 集成consul,消费者报I/O error on GET request for...
创建消费者微服务,去调用生产者微服务的请求过程中,出现以下错误: 报错原因 因为在使用SpringCloudAlibaba中的Nacos框架时,自动整合了SpringCloud中的Ribbon框架中的负载均衡,因为微服务提供者有两个,在消…...

pytest的测试标记marks
引用打标的marks文档 Python的pytest框架(5)--测试标记(Markers)_pytest执行指定的marker-CSDN博客 https://www.cnblogs.com/pipile/p/12696226.html 给用例自定义打标签的代码示例 #coding:utf-8 import pytest pytest.mark.smoke def test_1():print("smoke的测试用…...
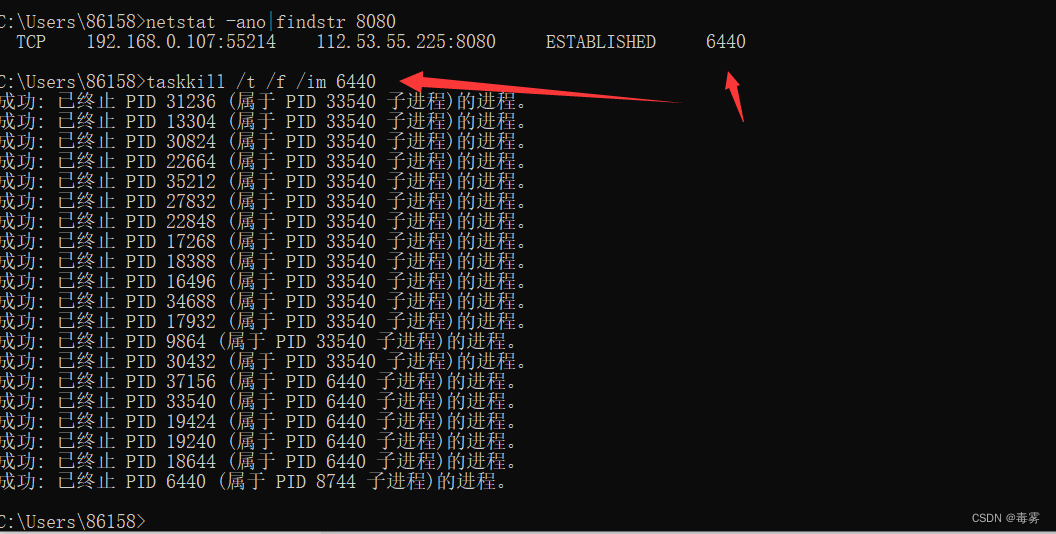
端口占用解决方法
1、查询端口 打开cmd命令提示符窗口,输入以下指令查询所有端口 netstat -ano //查询所有端口 netstat -ano|findstr 8080 //查询指定端口 2、杀死进程 taskkill /t /f /im 进程号(PID)...
Java毕设之基于springboot的医护人员排班系统
运行环境 开发语言:java 框架:springboot,vue JDK版本:JDK1.8 数据库:mysql5.7(推荐5.7,8.0也可以) 数据库工具:Navicat11 开发软件:idea/eclipse(推荐idea) 系统详细实现 医护类型管理 医护人员排班系统的系统管理员可以对医护类型添加修改删除以及…...
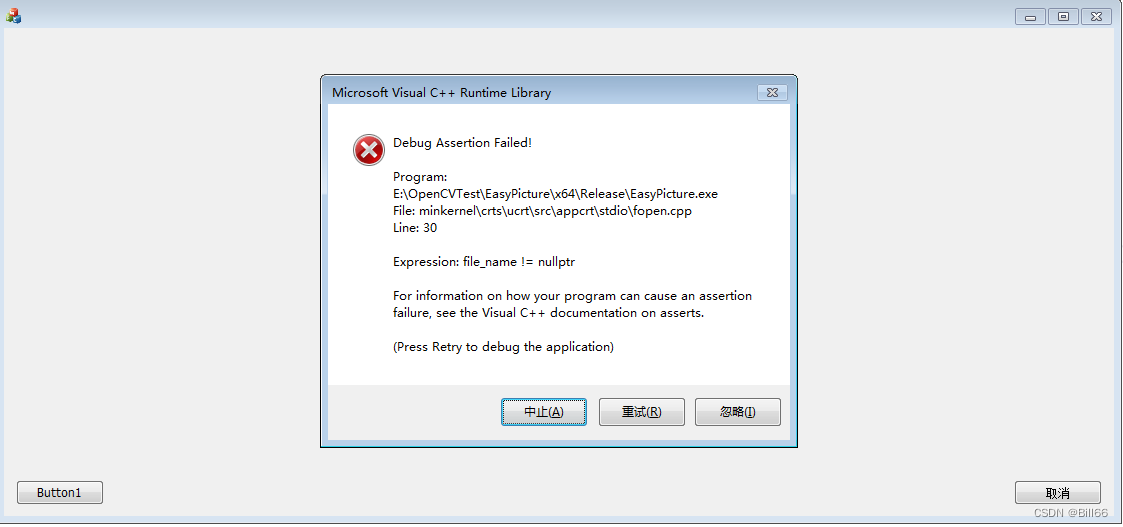
OpenCV4.8 VS2019 MFC编程出现的诡异现象
OpenCV4.8及OpenCV4.4 VS2019MFC编程在调用imred()函数时,debug X64试运行没问题。 release X64试运行时出现下面错误。 void CEasyPictureDlg::OnBnClickedOpen() {CFileDialog fdlg(TRUE, NULL, 0, OFN_HIDEREADONLY | OFN_OVERWRITEPROMP…...

游戏辅助 -- 三种分析角色坐标方法(CE、xdbg、龙龙遍历工具)
所用工具下载地址: https://pan.quark.cn/s/d54e7cdc55e6 在上次课程中,我们成功获取了人物对象的基址:[[[0xd75db8]1C]28],而人物血量的地址则是基址再加上偏移量278。 接下来,我们需要执行以下步骤来进一步操作&a…...

【VTKExamples::Rendering】第一期 TestAmbientSpheres(环境照明系数)
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 公众号:VTK忠粉 前言 本文分享VTK样例TestAmbientShperes,介绍环境照明系数对Actor颜色的影响,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我的动…...

代码随想录leetcode200题之栈与队列
目录 1 介绍2 训练3 参考 1 介绍 本博客用来记录代码随想录leetcode200题中栈与队列部分的题目。 2 训练 题目1:232. 用栈实现队列 C代码如下, #include <stack>class MyQueue { private:stack<int> a;stack<int> b; //辅助栈 pu…...
使用Python实现2048小游戏
使用Python实现2048小游戏源码分享。实现效果如下所示。 实现效果图 游戏开始效果图 游戏结束效果图 部分源码截图 下载链接 基于如下的运行环境。运行需要安装tkinter /Library/Frameworks/Python.framework/Versions/3.7/bin/python/bin/python /Users/nihui/Documents/P…...

漏洞管理是如何在攻击者之前识别漏洞从而帮助人们阻止攻击的
漏洞管理 是主动查找、评估和缓解组织 IT 环境中的安全漏洞、弱点、差距、错误配置和错误的过程。该过程通常扩展到整个 IT 环境,包括网络、应用程序、系统、基础设施、软件和第三方服务等。鉴于所涉及的高成本,组织根本无法承受网络攻击和数据泄露。如果…...
LNMT部署jpress
LNMT部署jpress 环境要求: MySQL版本5.6/5.7 tomcat版本9.0.65 源码安装MySQL5.7版 //源码安装MySQL5.7版1关闭防火墙 2创建mysql用户 3上传mysql5.7包(https://downloads.mysql.com/archives/get/p/23/file/mysql-5.7.30-linux-glibc2.12-x86_64.tar.g…...

汽车软件研发工具链丨怿星科技新产品重磅发布
“创新引领未来”聚焦汽车软件新基建,4月27日下午,怿星科技2024新产品发布会在北京圆满举行!智能汽车领域的企业代表、知名大企业负责人、投资机构代表、研究机构代表齐聚现场,线上直播同步开启,共同见证怿星科技从单点…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
